基于模态试验的夹具及产品模型修正

赵艳涛，陈耀，贾俊杰

（航天科工防御技术研究试验中心，北京 100854）

前言

模态试验与模态仿真是相辅相成的。建立的有限元模型后是否能够开展应用，需要对有限元模型进行校准，模态试验结果作为依据，通过修正有限元模型使模态仿真结果和模态试验结果一致。本文采用锤击法模态试验获取夹具、产品及组合体的各阶振型、模态频率等指标，作为修正有限元模型的依据，夹具、产品以及组合体分别依据模态试验结果进行有限元模型修正，经过修正后的有限元模型可以用来搭建虚拟振动系统。

1 模态分析的基本理论[1-3]

对于一个结构来说，模态频率、模态阻尼都是结构的本构特征，从数值上讲是常值。模态分析就是对结构频率响应谱中所有共振点模态进行识别从而得出结构特性。试验模态通过对结构的动态测试和信号分析，来确定结构的模态参数。

在有限元法中，当把结构离散化为各种单元，组装得到整个结构的运动方程为：

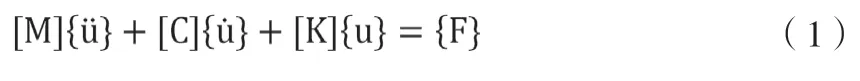
式中：

[M]—系统的质量矩阵；

[C]—系统的阻尼矩阵；

[K]—系统的刚度矩阵；

这是1个互相耦合的方程组，通过坐标变换将这个耦合的方程组变成一组正交的新的坐标系，即模态坐标，将复杂的多自由度系统简化为一系列单自由度系统。这个模态坐标中的固有频率、阻尼、质量、刚度等称为模态参数，各阶固有频率下的模型各部位的位移即为模态振型。

假设系统初始状态为零，对方程两边进行傅氏变换：

反映了i点激励到j点响应之间的传递关系函数。反映了i点激励对j点响应的贡献，即i点激励（其余部位激励力为零）时，j点响应与i点激振力之比。

解微分矩阵方程（1），得到其特征值和特征向量便得到系统的固有频率ωr和振型φr，振型具有正交性，同M、C、K均为实对称阵，故而可以利用φr组成矩阵Φ=[φ1，φ2，φ3…φN]，对M、C、K进行对角化，得：

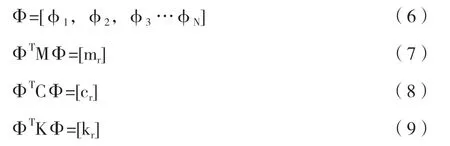
式中：

ωr—模态频率；

φr—模态振型；

mr—模态质量；

cr—模态阻尼；

kr—模态刚度，代入（4）中得到模态参数表示的频率响应函数矩阵。

可以看出，多自由度系统的频响函数是系统各阶特征值和特征向量的线性叠加。所以对线性系统来说，可以通过模态叠加的方法求得计算系统的响应。频率响应矩阵的任意一行或任意一列包含模态参数的足够信息。

完成模态试验并进行模态参数辨识后应该验证模态试验的质量，通常可采用模态置信矩阵（Modal Assurance Criterion, MAC）来判断模态振型的正交性。如果模态试验质量较好，那么模态置信矩阵的主对角元素应该为1，非对角元素为0[4]。

2 模态试验的基本流程

模态试验假设一个结构的模态可以在除节点外的任何一点激励出来，只需测频率响应函数矩阵H(ω)的一行（多点激励单点测量）或一列（单点激励多点测量）就可以了。因此这里采用单点激励、多点测量的方式。模态试验示意图如图1所示。力锤敲击激励点通过力传感器采集激励力信号，测点布置ICP传感器采集响应加速度信号，激励力和响应加速度信号进入数据采集系统，通过模态分析软件提取相应的传递函数进而识别出模态参数。

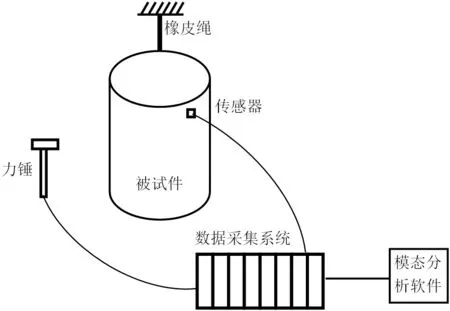
图1 模态试验示意图

采用橡皮绳悬挂法，在这种“自由状态”下可以测得更真实的结构模态。悬挂频率低于1 Hz，夹具和产品的弹性振动固有频率在30 Hz以上，远低于被测试件的一阶谐振频率。避免了悬挂系统对被测试件固有特性的影响。

被测试验件为中小型结构且为低阻尼结构，因此激励方式采用锤击法，不会给被测结构件附加任何质量而影响其的动态特性。信号处理加矩形窗。锤击法能量小，测量信噪比低，采用5次敲击的数据平均处理来消除噪声的干扰，锤击过程中避免连击，每一次激励的时间间隔不少于5 s。根据被测试件的质量和刚度，选择合适的锤头质量、锤头材料，结合敲击者的经验，在整个频段上相干越接近1越好，相干性作为判断力锤敲击测得的频响函数（FRF）好坏的依据。信号采集需要选用合适的量程，使激励和响应在合适的范围内，量程过大采集信号不准确，量程过小会出现信号截断，保证每一次激励和响应信号测试的有效性。

激励点如果选择在节点上就激发不出来相应的模态，为了避免这种情况，通常要选用两个以上激励点开展模态试验来进行相互备份和验证。测得几个频响函数并进行比较，选择曲线光滑、清晰的频响函数，将关心频段内相干达到0.9以上的点为激励点。

测点采用均匀分布的原则，传感器的选择和安装对测量结果都具有重要的影响，传感器要求动态范围宽、工作频段宽、低频性能好、线性度好、体积小、质量小[5]。

3 夹具及产品的模态试验及模型校准

建立有限元模型，在保证模态试验结果可信的基础上修正有限元模型，使模态仿真和模态试验结果一致。修正模型的过程如下：在振型一致、几何模型与实物相符的前提下调整材料参数，在参考材料基本参数的基础上，首先微调密度来保证质量与实际质量一致，再微调弹性模量，使模态仿真结果与模态试验结果比较接近，固有频率最大相对误差在5%以内。则可认为有限元模型是可信的。

3.1 夹具的模态试验及模型校准

夹具为平板状夹具，见图2。先开展夹具的模态试验，将模态试验结果作为参照，夹具模态试验的MAC矩阵如图3。在保证夹具质量和实物一致的前提下，微调弹性模量，使夹具模态仿真结果和模态试验结果一致,夹具模态仿真结果和模态试验结果见表1。夹具的参数为：密度：2 707 kg/m3，弹性模量：7.1×1010Pa ， 泊松比0.33。

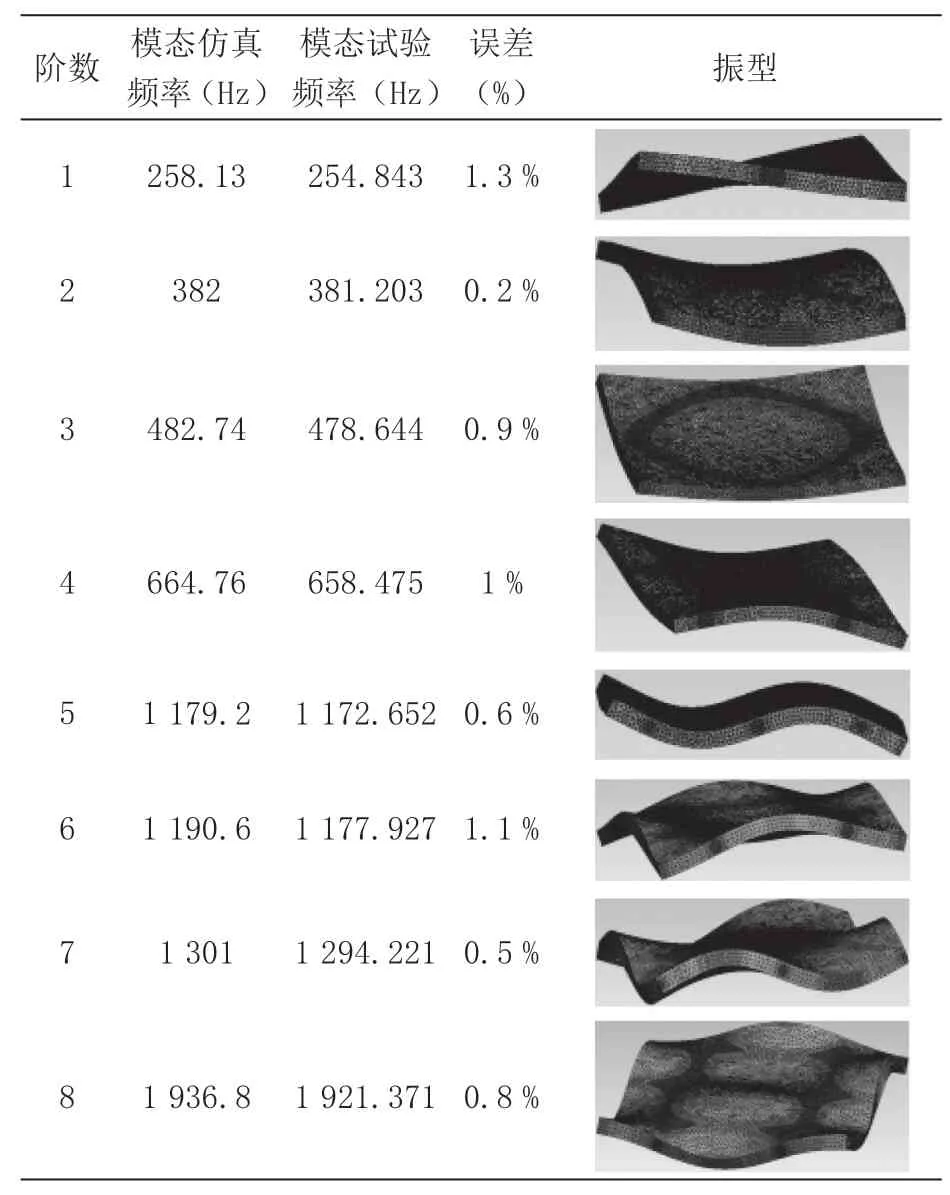
表1 夹具模态仿真和模态试验固有频率比较

图2 夹具

图3 夹具模态试验MAC矩阵

3.2 产品的模态试验及模型校准

产品为类圆筒状结构体。先开展产品的模态试验，将模态试验结果作为参照，产品模态试验的MAC矩阵如图4。和前文的模型修正方法相同，在保证产品质量和实物一致的前提下，微调弹性模量，使产品模态仿真结果和模态试验结果一致,产品模态仿真结果和模态试验结果见表2。修改后产品的参数为：密度：2 850 kg/m3，弹性模量：7.5 e10 Pa，泊松比0.3。

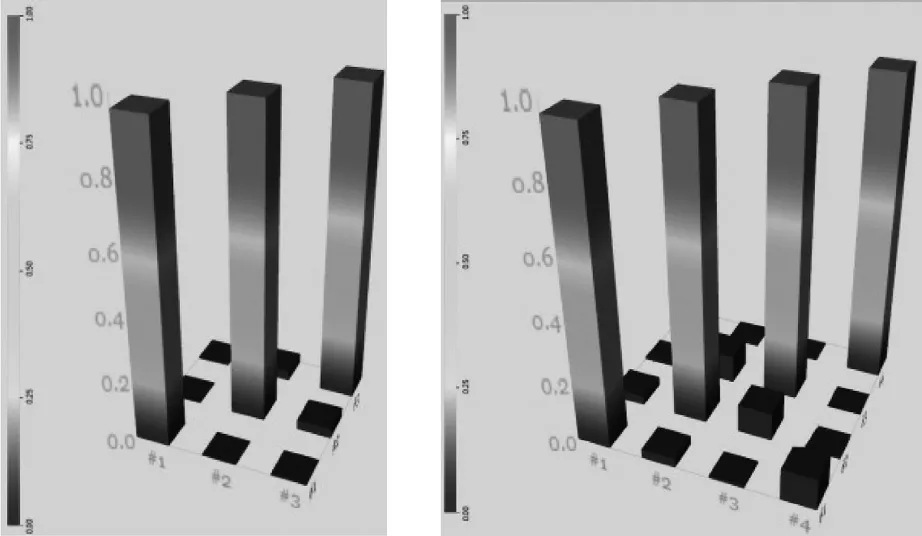
图4 夹具模态试验MAC矩阵图5 组合体模态试验MAC矩阵

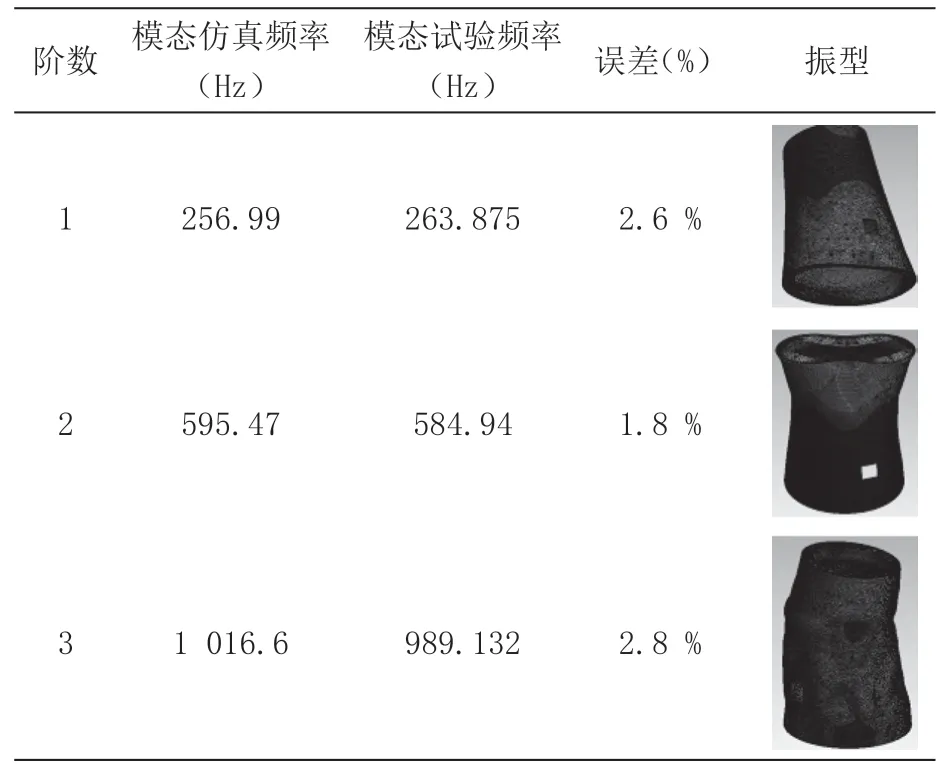
表2 产品模态仿真和模态试验固有频率比较

3.3 组合体的模态试验及模型校准

将模型和参数修改后的夹具和产品组合在一起，实物采用螺栓连接并开展模态试验，将模态试验结果作为参照。在有限元软件里将螺栓连接处采用固定约束。组合体模态试验的MAC矩阵如图5，组合体模态仿真结果和模态试验结果见表3。

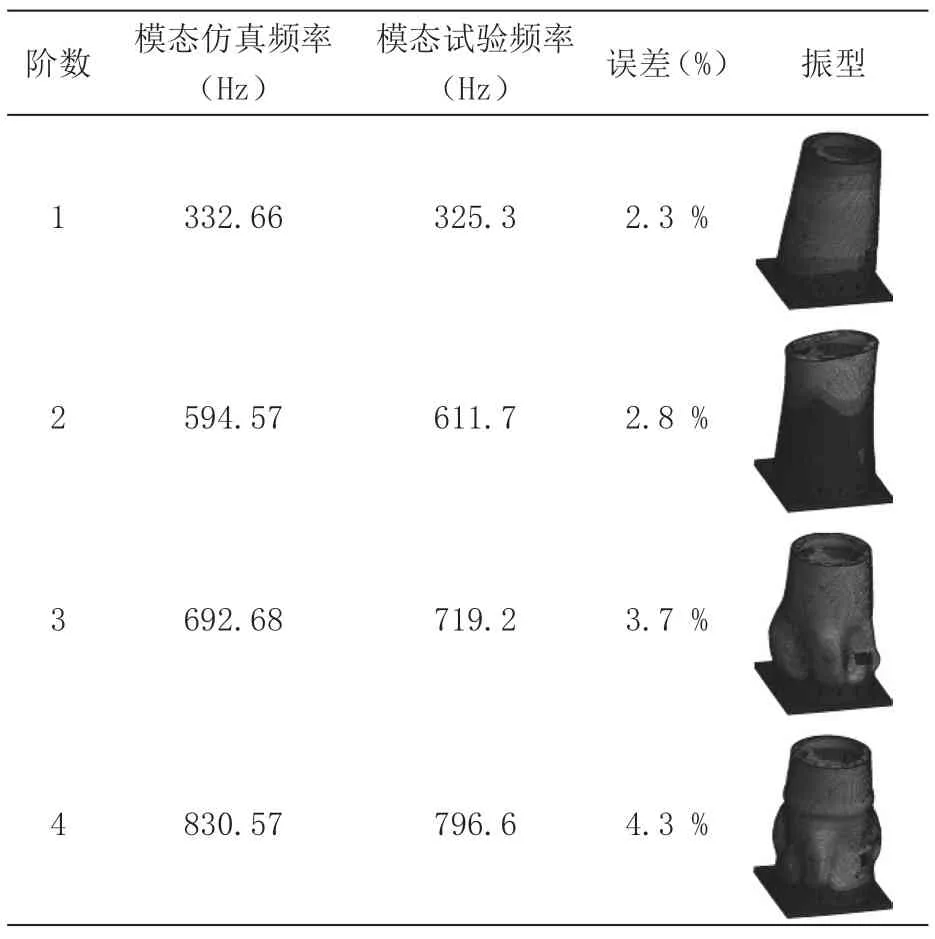
表3 组合体模态仿真和模态试验固有频率比较

模态试验和模态仿真是相辅相承的。一方面，在模态试验前可以开展初步开展模态仿真，在大致了解了模态振型、节点等信息后，可以为模态试验的测点、激振点的布点提供参考，避免激振点布置在节点，另外要布足够的测点以及选择合适的测点方向从而能完整表征振型。参考仿真的模态振型结果而不参考仿真的模态频率结果，如果测点布置不够，模态试验就不容易分辨出振型来。另一方面，模态试验结果作为修正模态仿真结果的依据，在二者振型对应一致的前提下修改有限元模型使二者的模态频率也对应一致，在建有限元模型时会对模型进行简化，材料参数和实际也会存在差异，因此模态仿真结果会和模态试验结果存在差异。根据模态试验结果来修正有限元模型，包括适当修改材料参数，优化网格等方法来使模态仿真结果和模态试验结果在模态频率和模态振型都一致起来。另外模态试验结果和模态仿真结果不是一一对应的，往往仿真结果会比试验结果的模态数量多，因为模态试验时布置的测点是有限的，特别是高频段实际模态比较密集，很多模态识别不出来，模态试验结果和仿真结果会存在较大的差异。所以在修正有限元模型的过程中，要结合振型进行比对，对前几阶的重要模态进行对比和修正，使仿真结果和试验结果对应。经过模态试验修正过的有限元模型才具有工程实用价值。系统的响应可以看做各阶模态振型响应的叠加[6]。

4 总结

模态试验是进行有限元模型校准的有效手段，建立了夹具、产品、组合体在自由状态下的有限元模型，并逐级分别进行相应的模态试验，将模态试验结果作为参照，校准有限元模型，使仿真结果和试验结果的主要模态频率误差在5 %以内，满足工程上的精度要求，则可以认为有限元模型是可信的，可以应用于后续的虚拟试验。