基于时空地理加权回归模型的中国肺结核发病情况及影响因素研究

赵明扬，周乾宇，王荣荣，王宗熹，何雯倩，张文森，张恒榛，田卓旸，吴柯，王碧瑶，孙长青，*

肺结核是由结核分枝杆菌引起的具有强烈传染性的慢性呼吸系统传染病，是危害人体健康的重大传染病之一［1］。肺结核患者在排菌期，即痰菌阳性时具有传染性，1例未经治疗的排菌期活动性肺结核患者1年内可感染15～20名接触者。2019年全球结核报告显示，全世界每年约有1 000万人感染结核病，潜伏性结核感染人数占世界人口总数的1/4左右；中国新发结核病病例833 000例，发病率为58/10万，位居世界第三，是结核病高负担国家，肺结核防控形势依旧严峻［2］。

随着地理信息技术的发展和完善，大量基于空间计量学的空间统计分析方法被提出，地理信息系统和空间统计学在各领域得到广泛应用。英国学者Fotheringham提出的研究空间关系和空间相关关系的地理加权回归（geographical weighted regression，GWR）模型可以直观地探测空间关系的非平稳性［3］，并在多学科领域得到广泛应用［4-6］。但GWR模型只将数据的空间特性纳入模型，而忽略了时间特性对其的影响，在处理某些时间特性和空间特性均突出的数据资料时存在一定局限性。因此，香港大学黄波教授在GWR模型的基础上提出了时空地理加权回归（geographically and temporally weighted regression，GTWR）模型［7］。此模型能够更好地对数据的时空分布及特性进行评估，有效解决了回归模型的时空非平稳性，一经提出便得到广泛关注，并在众多学者的应用过程中不断完善［8-10］。

近年来，国内外学者对肺结核的时空分布进行大量研究表明，肺结核具有较强的时间特性和空间特性［11-13］。但现有研究更多的是对肺结核发病的影响因素进行独立的时间或空间回归分析，研究结果存在局限性，例如使用差分整合滑动平均自回归模型（autoregressive integrated moving average model，ARIMA）对肺结核数据进行时间序列分析时，忽略了其对应的空间因素的影响［14-15］；在使用空间聚类和地理加权回归时，肺结核数据所具有的时间特性便无法体现［16］。因此，将时间因素和空间因素同时进行回归分析，采用GTWR模型对影响肺结核发病的影响因素进行拟合分析是十分必要的。

综上所述，本文将使用GTWR模型探索中国肺结核分布的时间和空间异质性，并分析肺结核发病情况与气象和空气质量因素在时间和空间上的相关关系，为制订相应结核病防控措施提供科学参考。

1 材料与方法

1.1 数据来源 本研究使用的肺结核发病情况相关数据来源于公共卫生科学数据中心（https://www.phsciencedata.cn/Share/）中的2016—2018年全国分地区（除香港、澳门、台湾外的31个省份）肺结核分月统计数据，选取的指标为发病率（每10万人中病例数）。气象资料数据（包括月平均气温、湿度、风速等）来源于天气后报网（http://www.tianqihoubao.com/）。空气质量指数数据（包括PM2.5、PM10、SO2、NO2、CO、O3等的月平均浓度）来源于空气质量指数历史数据网站（https://www.aqistudy.cn/historydata/）。本研究所使用地理信息资料来源于国家基础地理信息中心（http://www.ngcc.cn/），文中涉及的中国地图均基于自然资源部标准地图服务网站 （http://bzdt.ch.mnr.gov.cn/）下载的审图号为GS（2019）1823号的标准地图制作。

本研究使用数据均来源于公共数据库，不适用伦理审查。

1.2 研究方法

1.2.1 多重共线性 多重共线性是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。因此，为保证回归模型的合理性，应在构建模型前对备选自变量的共线性进行分析。方差膨胀因子（VIF）是常用的检测自变量之间多重共线性的指标［17］。本研究将采用VIF对肺结核发病情况与影响因素之间的关系进行共线性检验，以避免由于影响因素之间的高度共线性而影响回归分析结果，其计算公式如下：

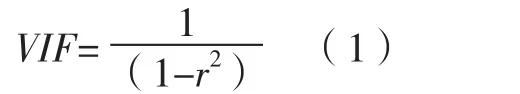
其中，r为线性回归中的决定系数，反映了回归方程解释因变量变化的百分比。VIF越大，说明解释变量之间存在共线性的可能性越大，若VIF均在0～10，则影响因素之间不存在高度共线性，可直接进行回归分析［18］。

1.2.2 空间自相关 使用空间计量学方法的前提是样本数据之间存在空间异质性，因此在构建GWR和GTWR模型前需对自变量进行空间自相关分析。通常使用莫兰指数（Moran'sⅠ）进行全局空间自相关分析，以确定所研究样本点的某一属性值与领域内其他样本点相同属性值在空间上是否关联。本研究将通过计算全局Moran'sⅠ以确定肺结核发病情况的空间自相关性，其计算公式如下：

其中，S0为所有样本点之间空间权重的总和，zi为样本点i的某一属性值与其平均值的偏差。Moran'sⅠ的取值在-1～1，若指数为正值则表示样本的某一属性值在空间上呈现聚集状态，且指数越趋近1则聚集程度越强；若指数为负值则表示样本属性值呈离散分布；指数为0则表示样本属性值呈随机分布，无显著特征。

1.2.3 回归模型构建 本研究分别构建最小二乘法（OLS）模型、GWR模型和GTWR模型对肺结核发病情况进行实证分析，并比较模型优度以确定GTWR模型是否为处理肺结核数据的最佳模型。

OLS模型是常用的传统线性回归模型，该模型仅对参数进行了平均或全局意义上的估计，但无法体现各参数在空间上的非平稳性。模型计算公式为：

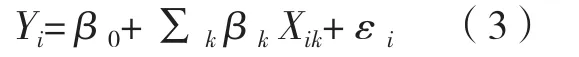
其中，Yi表示第i个样本点的因变量，β0表示线性回归方程的截距，βk表示第k个自变量的回归系数，Xik表示第i个样本点的第k个自变量，εi表示随机误差。

GWR模型是基于传统线性回归模型改进后的模型，其主要优势是能够将空间权重矩阵运用在线性回归模型之中，可以更好的展现结果的空间结构分异。模型计算公式为：

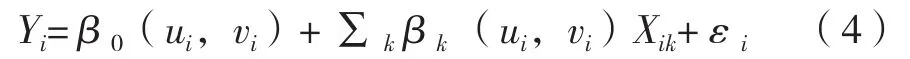
其中，Yi表示第i个样本点的因变量，ui表示第i个样本点的经度坐标，vi表示第i个样本点的纬度坐标，（ui，vi）表示第i个样本点的空间经纬度坐标，β0（ui，vi）表示第i个样本点的常数项，βk（ui，vi）表示第k个自变量在第i个样本点的回归系数，Xik表示第i个样本点的第k个自变量，εi表示随机误差。

GTWR模型是在GWR模型的基础上将时间赋值到局部样本点数据集上，求解局部样本点i的参数，充分利用样本数据的时间特性，提高参数估计的准确性。模型计算公式为：

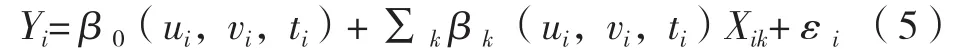
其中，Yi表示第i个样本点的因变量，ui表示第i个样本点的经度坐标，vi表示第i个样本点的纬度坐标，ti表示第i个样本点的时间坐标，（ui，vi，ti）表示第i个样本点的时空维度坐标，β0（ui，vi，ti）表示第i个样本点的常数项，βk（ui，vi，ti）表示第k个解释变量在第i个样本点的回归系数，Xik表示第i个样本点的第k个自变量，εi表示随机误差。

GWR与GTWR模型的参数方法如下：

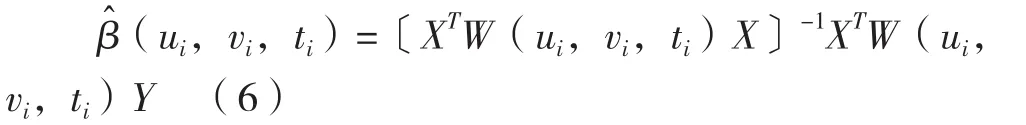
其中，空间权重矩阵W是由空间带宽、核函数、距离计算公式共同决定。根据既往文献［7］，本研究将基于最小交叉验证（CV）值、高斯（Gaussian）核函数和欧式距离（Euclidean distance）来共同构建模型。模型优度通过比较修正后的赤池信息量（AICc）与R2值来评估，R2值越大，AICc值越小，说明自变量对因变量的解释度越强。

1.2.4 统计分析 使用均数、最小值、最大值、四分位数间距来描述GTWR模型的拟合系数。基于GTWR模型的拟合系数，分别绘制各个变量的核密度图和时空分布图。使用自然断裂点法对相似度较高的数据进行分组，同时强行将“0”设置为区间值，以区分正系数和负系数，当拟合系数为正值时，表示自变量对因变量具有促进作用；当拟合系数为负值时，表示自变量对因变量具有抑制作用，且拟合系数的绝对值越大，作用程度越大。

本研究使用R 4.1.3软件进行统计描述，使用Arc GIS 10.7软件进行模型参数估计和模型构建。

2 结果

2.1 肺结核发病情况的时空分布 2016—2018年全国肺结核发病率的空间分布见图1：我国肺结核总发病率在逐年下降，且空间分布较为集中。肺结核发病率较高的地区主要集中在新疆、四川、西藏、青海、贵州、广西等。其中，新疆的肺结核发病率连续3年处于最高水平；四川的肺结核发病率在2016年处于较高水平，但随后2年发病率大幅下降；西藏、青海的肺结核发病率在2016年处于较低水平，但随后2年发病率大幅增加。肺结核发病率较低的地区主要集中在宁夏、天津、上海、北京、海南等。

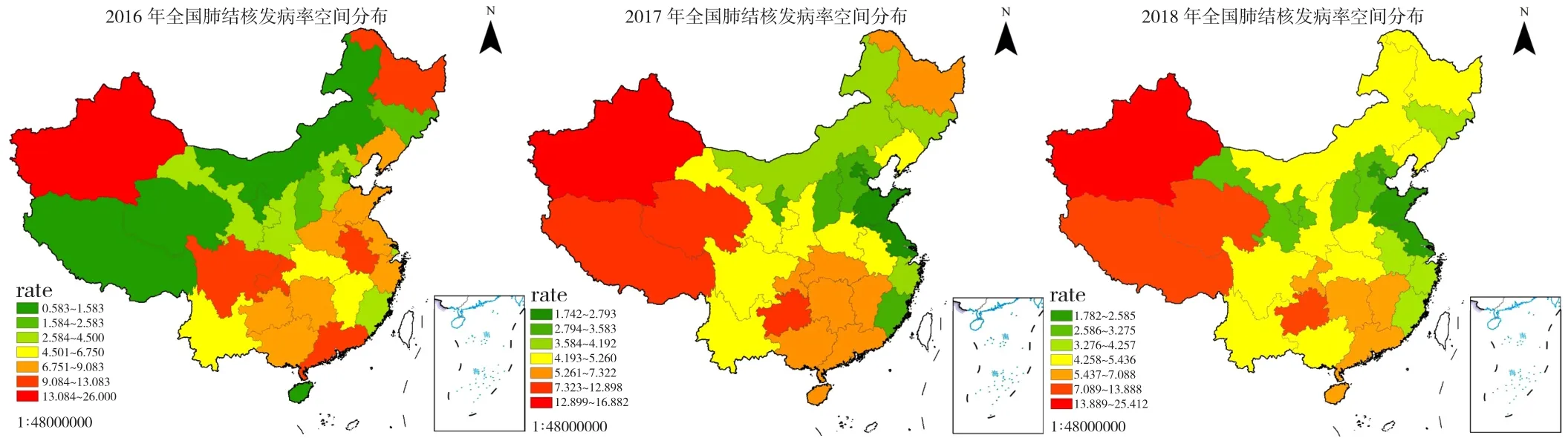
图1 全国肺结核发病率空间分布图Figure 1 Spatial distribution of pulmonary tuberculosis incidence in China during 2016—2018

2.2 模型对比结果 经过多重共线性和空间自相关检验（全局Moran's I= 0.376），剔除气温这一具有强共线性的变量（VIFTmax=48.01，VIFTmin=48.34）后，分别建立OLS、GWR和GTWR模型，评估并比较模型优度，结果如表1所示。GTWR模型的R2值与AdjustedR2值均比OLS和GWR模型要高，同时GTWR模型的AICc值均比OLS和GWR模型要小，表明GTWR模型能更好地解释自变量对肺结核发病情况的影响，更能解释具有时空特征的数据。

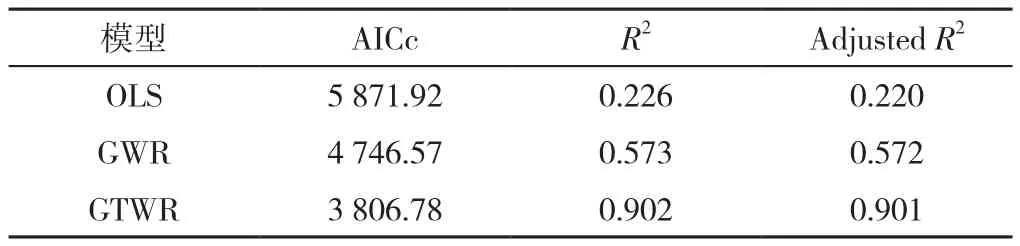
表1 OLS、GWR、GTWR模型比较的结果Table 1 Values of AICc，R2 and adjusted R2 of OLS，GWR and GTWR models

2.3 拟合系数的时空特性 使用均数、最小值、最大值、四分位数间距来描述GTWR模型的拟合系数，结果如表2所示。基于GTWR模型的拟合系数结果绘制每个变量的核密度图，结果如图2所示。拟合系数的核密度图结果显示：自变量风速呈现多峰分布，主峰约为-0.5；自变量湿度呈现多峰分布，主峰约为0.01，且各峰系数均大于0；自变量PM2.5呈现左偏峰分布，主峰约为-0.01；自变量PM10呈现单峰分布，主峰约为0.005；自变量SO2呈现多峰分布，主峰约为0；自变量NO2呈现多峰分布，主峰约为-0.03；自变量CO呈现右偏峰分布，主峰约为-0.5；自变量O3呈现多峰分布，主峰约为0。

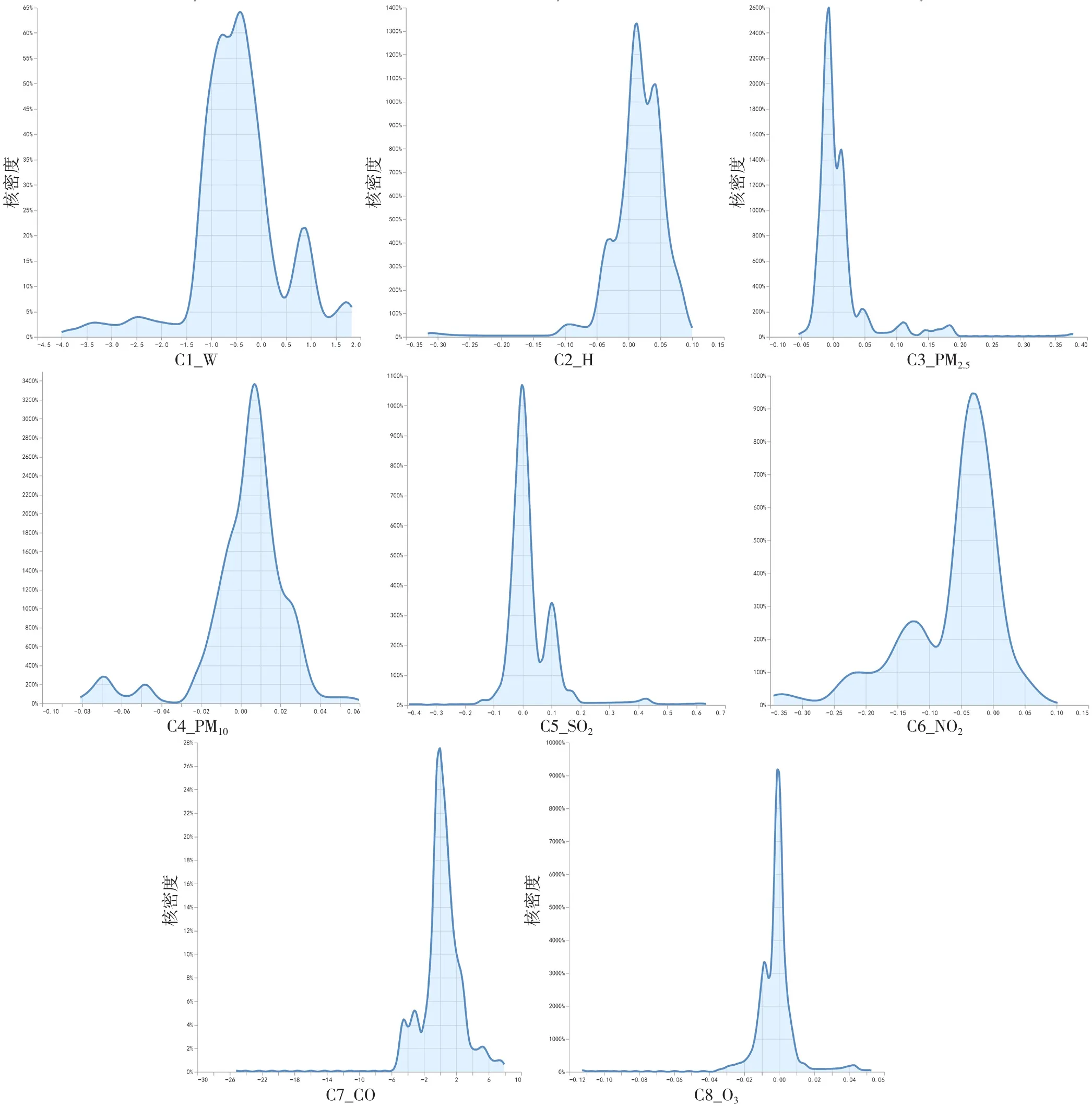
图2 各变量拟合系数的核密度分布图Figure 2 Kernel density estimation of fitting coefficients of each variable

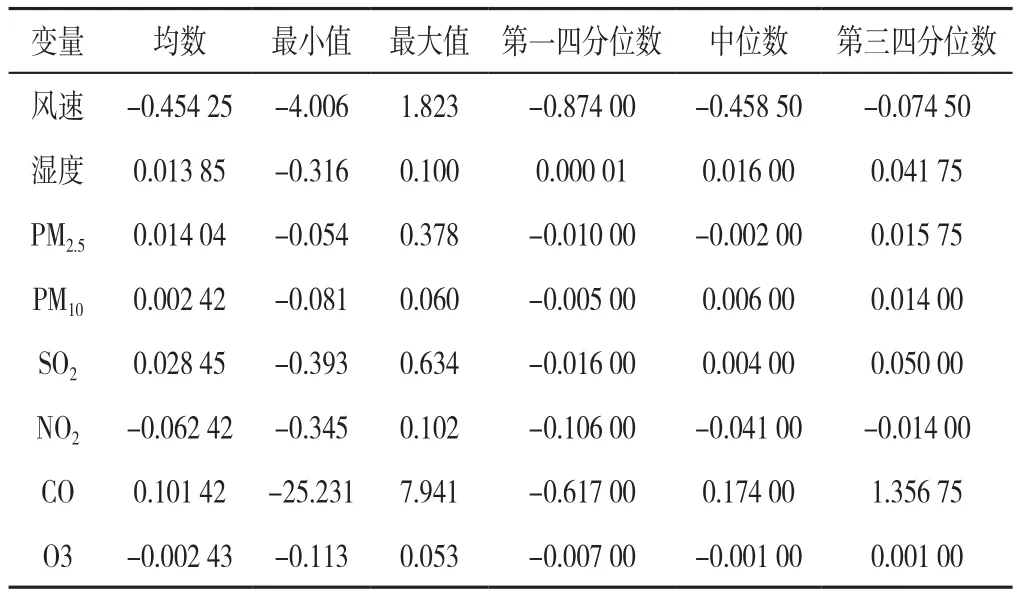
表2 GTWR模型的拟合系数Table 2 Fitting coefficients of meteorological and air quality factors included in GTWR model

基于GTWR模型的拟合系数，分别绘制各个变量的时空分布图（图3）。拟合系数的时空分布图结果显示：自变量风速呈现中部和东南部的拟合系数较低、东北和西部的拟合系数较高的分布格局，其中风速对青海、甘肃、湖南、江西等地区的肺结核发病率具有显著的抑制作用，对西藏、新疆、黑龙江等地区的肺结核发病率具有显著的促进作用；自变量湿度呈现西部和北部的拟合系数较低、东南和南部的拟合系数较高的分布格局，其中湿度对海南、广东、广西等地区的肺结核发病率具有显著的促进作用；自变量PM2.5呈现东北部和中东部的拟合系数较低、西南部和西部的拟合系数较高的分布格局，其中PM2.5对广西、云南、新疆、西藏等地区的肺结核发病率具有显著的促进作用；自变量PM10呈现中部和西部的拟合系数较低、东南部和中东部的拟合系数较高的分布格局，其中PM10对浙江、上海、福建等地区的肺结核发病率具有显著的促进作用；自变量SO2呈现中部和北部的拟合系数较低、西部和南部的拟合系数较高的分布格局，其中SO2对西藏、广东、新疆等地区的肺结核发病率具有显著的促进作用；自变量NO2呈现西北部和西南部的拟合系数较低，东北部、中部的拟合系数较高的分布格局，其中NO2对黑龙江、吉林等地区的肺结核发病率具有显著的促进作用；自变量CO呈现西部和西南部的拟合系数较低、东南部和中西部的拟合系数较高的分布格局，其中CO对福建、青海、甘肃等地区的肺结核发病率具有显著的促进作用；自变量O3呈现西北部和南部的拟合系数较低、东北部和西南部的拟合系数较高的分布格局，其中O3对新疆、浙江、福建等地区的肺结核发病率具有显著的促进作用。

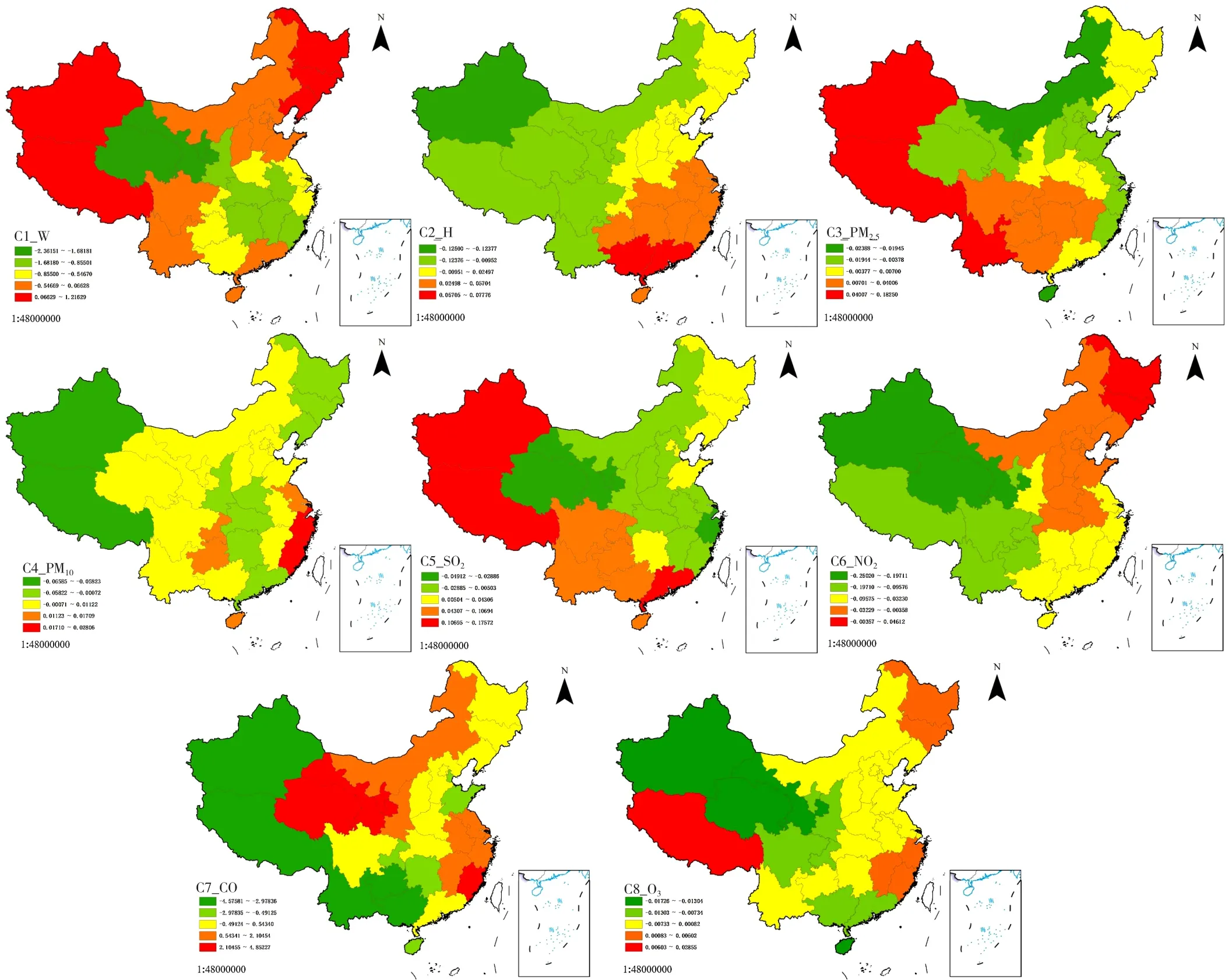
图3 各变量拟合系数的时空分布图Figure 3 Spatial and temporal distribution of fitting coefficients of each variable

3 讨论

本研究构建模型前预先进行了多重共线性检验，结果显示，自变量气温具有强共线性。既往研究也表明气温与其他呼吸系统疾病危险因素具有交叉协同效应。马盼等［19］研究显示，高温、高湿共同作用下将对儿童的呼吸系统健康造成更严重的后果，而低温、低湿共同作用下将增加老年人的呼吸系统疾病患病风险。一项基于医院门诊数据的时间序列分析结果显示，气温和各种污染物浓度之间存在明显的交互作用，尤其是低温与高浓度污染物共同作用下，对呼吸系统门诊就诊人数的影响最大［20］。由于多重共线性数据可能会影响GTWR模型分析的精度，本研究未将气温这一具有强共线性的变量纳入模型。

3.1 各变量拟合系数的核密度分布图分析 各变量拟合系数的核密度图结果显示：自变量风速的主峰系数为负值，且各峰系数有正有负，表明自变量的增加对大多数地区的肺结核发病情况呈现显著的保护作用，但在部分地区仍具有显著的促进作用；自变量湿度、SO2的主峰系数为正值，且各峰系数均＞0，表明自变量的增加将显著促进肺结核发病率的增加；自变量PM2.5、NO2、CO、O3呈现多峰分布，且各峰系数有正有负，表明自变量的增加对大多数地区的肺结核发病率的增加呈现显著的促进作用；自变量PM10呈现单峰分布，主峰系数为正值，表明自变量的增加将显著促进大多数地区肺结核发病率的增加。

3.2 各变量拟合系数的时空分布图分析 GTWR模型的显著优势是其拟合系数可以反映自变量对因变量影响的时空变异特征。本研究分别绘制了各变量拟合系数的时空分布图，结果显示：自变量风速对青海、甘肃、湖南、江西等城市的肺结核发病率的增加具有显著的抑制作用，对西藏、新疆、黑龙江等地区的肺结核发病率的增加具有显著的促进作用。既往研究表明，风速对肺结核发病存在促进作用［21］，较大的风速可降低气温，从而间接增加肺结核发病风险。针对本研究的双向作用，可能存在的原因是：西藏、新疆属于高海拔地区，东三省的平均气温本就偏低，这些地区更易受到风速的影响导致气温下降，从而使肺结核发病风险增加，因此这类地区应在大风天气注意保暖以预防疾病。而湖南、江西等地的平均温度较高，温度不易受风速影响，较大风速还会降低其空气污染物浓度［22］，进而使肺结核发病风险降低。

自变量湿度对海南、广东、广西等地区的肺结核发病率增加具有显著的促进作用。这与既往研究中较高湿度能增加肺结核发病风险的结论相符合［18，21］。可能存在的原因是：在一定范围内，较高的湿度将增加结核杆菌在空气中停留存活的时间，从而增加了人群感染结核杆菌的风险。因此，针对这类地区应注意对家具或生活用品的勤加晾晒，尽量保持生活环境的干燥。

自变量PM10对浙江、上海、福建等地区的肺结核发病率具有显著的促进作用。这与既往研究中PM10暴露浓度增加将导致肺结核发病风险增加的结论相符［23］。可能存在的原因是：PM10等可吸入颗粒物能够伴随呼吸进入人体，并在肺部沉积，可能会损伤肺泡及黏膜，导致肺部组织慢性纤维化等情况发生，降低肺部抵抗力；此外，PM10等空气污染物还可以与空气微生物结合［24］，明显增加结核病菌侵入人体的概率。因此，针对这类地区应注意在空气污染程度较高时避免户外活动。

既往研究表明空气污染物（PM2.5、SO2、NO2、CO、O3）的浓度增加会显著增加肺结核的发病风险［23，25-26］，本研究的大部分结果也能够与该结论相互验证。但上述几类空气污染物作为自变量也存在部分拟合系数为负数的现象，这部分结果与既往研究结论相悖。造成这一现象的原因可能是：由上述结论可知，拟合系数为负数的城市主要为江苏、上海、广东等沿海地区和西藏、新疆、青海等高海拔地区，此类地区的空气质量较好，空气污染物浓度较低，因此空气污染物对于此类地区肺结核发病情况的促进作用不显著。但模型构建过程中，在与其他地区、其他变量共同分析时，尤其是与空气质量较差地区做对比，且存在其他保护因素时，此类自变量在承担部分结果解释的功能后，最终导致过低浓度的空气污染物呈现负拟合系数的现象。针对大部分城市的空气污染物对肺结核发病人数的促进作用，应采取积极措施改善空气质量，降低空气污染物浓度；在空气污染物浓度较高的时候尽量避免外出，在室内即时关窗，以减少接触空气污染物，从而降低肺结核发病风险。

本研究存在一定的局限性。第一，为避免新型冠状病毒肺炎造成的影响，尤其是疫情防控间接导致其他呼吸系统疾病发病率的减少［27］，本研究选取2016—2018年的数据进行分析，所反映的结果可能与当前疫情形势下的实际情况有所偏差。第二，由于本研究数据存在较强的共线性，可能会导致模型结果存在一定偏差，研究组计划后续使用更多数据集去验证模型及研究结果。第三，既往研究显示，气象因素与空气质量因素不仅对当天肺结核发病情况有显著影响外，还存在3～5 d的滞后效应［23，28］，但本研究因数据局限并未能对其进行验证。第四，影响肺结核发病情况的因素还包括生活方式、教育水平、经济状况等，但由于相关数据缺乏可及性，本研究并未将其纳入。因此，研究组计划后续引入更新、更全面的数据集来提高模型的适用性和稳健性。

本研究基于2016—2018年全国数据构建的GTWR模型很好地展示了中国肺结核发病情况的时空分布，并详细阐述了气象因素和空气质量因素与肺结核发病情况的显著相关关系及其时空特异性。在实际疾病预防工作中，应结合不同地区的不同影响因素，针对性的制定疾病预防措施。例如：高海拔地区大风天气注意保暖；湿度较高地区应注意除湿；空气质量较差地区应积极采取措施改善空气质量，并注意避免高空气污染物浓度时的户外活动。

作者贡献：赵明扬负责提出概念、数据管理、形式分析、原稿写作等工作；周乾宇负责方法学、监督审查和编辑写作等工作；王荣荣、王宗熹、何雯倩、张文森、张恒榛、田卓旸、吴柯、王碧瑶负责数据管理工作；孙长青负责资金支持、项目管理、监督、审查和编辑写作等工作。

本文无利益冲突。