4.3 K ～ 299 K温区Cu-ETP热膨胀系数原位实验测量研究

刘文静，张海洋，高 波，郑嘉熹，韩东旭，罗二仓，PITRE Laurent

1) 中国科学院理化技术研究所中法低温计量科学与技术国际联合实验室，北京 100190 2) 中国科学院理化技术研究所中国科学院低温工程学重点实验室，北京 100190 3) 中国科学院大学，北京 100049 4) 北京石油化工学院，北京 102617 5) 法国国家计量院-法国国立科学技术与管理学院，拉普莱纳-圣德尼 F93210

2019年5月20日世界计量日，国际单位制发生了重大变革，自此，七个基本单位全部由基本物理常数定义.其中，热力学温度单位开尔文（K）将根据玻尔兹曼常数重新定义[1].在基准测温领域，国际温度咨询委员会推荐了几种基准气体测温方法[2]：介电常数气体测温法[3]、声学气体测温法[4]和折射率气体测温法[5−6].其中，声学法和折射率法通常采用准球形谐振腔结合微波谐振频率测量技术进行热力学温度测量.谐振腔的材料通常为金属材料—电解沥青铜（Cu-ETP）[7]，其一个特性是具有高导电性，微波谐振法使用的电磁波属于交变电流，当电磁波在金属谐振腔体内传播时，电磁场会集中在材料的表面形成感应电流，从而产生趋肤效应[8]，Cu-ETP材料的高导电性使得谐振腔具有趋肤效应低的优点；该材料的另一特性是高导热性，会使得谐振腔兼备低温热响应快的优点[9].

Cu-ETP是一种重要的材料，在航空航天和温度计量等领域有着广泛的应用，其准确的材料特性是必不可少的，如热膨胀系数和等温压缩系数等.材料线性热膨胀系数的测量在温度计量行业至关重要，其温度依赖特性在机械结构设计及应用等领域是不可或缺的，特别是在低温工程领域，实验装置由具有不同热性能和机械性能的部件组成.等温压缩系数在折射率气体测温中起着极其重要的作用[10−11]，精确的材料热膨胀系数是获得高准确度等温压缩系数的前提之一.

由于Cu-ETP的热膨胀系数和等温压缩系数原位测量数据缺失，在基准测温领域国际同行通常以高导无氧铜（OFHC）物性作为Cu-ETP物性近似处理，这可能会引入固有测量误差.因此，需要获得一组高准确的Cu-ETP线性热膨胀系数，它也可用于检验微波谐振频率测量的准确性和测温的可靠性.

热膨胀系数表示材料在热载荷下的尺寸稳定性[12]，其测定要求为对正在经历适当热循环的材料样品测量两个物理量，分别为尺寸和温度.当样品放置在真空下测量时是一种绝对技术，此时的测量精度最高[13].因此，本文的实验均是在真空条件下开展的线性热膨胀系数测量.根据样品的材料、尺寸、形状、温度范围和要求的精度，可采用多种方法进行温度小于300 K[14]时材料的热膨胀系数测量，例如，通过干涉式膨胀计[15]、电容式膨胀计[16]、光学膨胀计[17]、压缩膨胀计[18]或微波谐振法[19−20]，其中，微波谐振法是一种原位、精度高的测量方法，已获得较为广泛的应用[21−24].

本文基于多模式微波谐振法，采用降温法和控温法两种实验方法原位测量了4.3 K到299 K温区Cu-ETP线性热膨胀系数.本文首先介绍了热膨胀系数的实验测量方法，后续介绍了其实验测量系统，最后介绍了两种方法的测量结果，这两种方法均采集了多组实验多个微波模式的微波谐振频率数据，研究了各轮实验的重复性、微波模式一致性以及热膨胀系数的测量不确定度，结果显示Cu-ETP线性热膨胀系数测量结果具有良好的微波模式一致性.通过原位实验测量，得到了一组准确度高的线性热膨胀系数数据，并基于此发展了线性热膨胀系数关联方程，这在等温压缩系数测量和数据的预处理中是必不可少的，也为热力学温度的测量提供了高准确度的基础物性数据.

1 实验方法

1.1 微波谐振频率测量方法

微波谐振频率的测量过程如图1所示.采用双端口网络分析仪（Agilent N5241A）作为微波信号源，微波信号经1端口通过微波电缆、上天线传输至低温端谐振腔中，在谐振腔中微波信号进行谐振，谐振后的共振信号由下天线接收并通过另一根微波电缆传回到网络分析仪的2端口，实验所用源频率f和散射参数S21通过Labview软件采集记录.为提高源频率的准确度，采用GPS/GNSS时间或频率标准系统（FS740）为网络分析仪提供10 MHz频率参考信号.

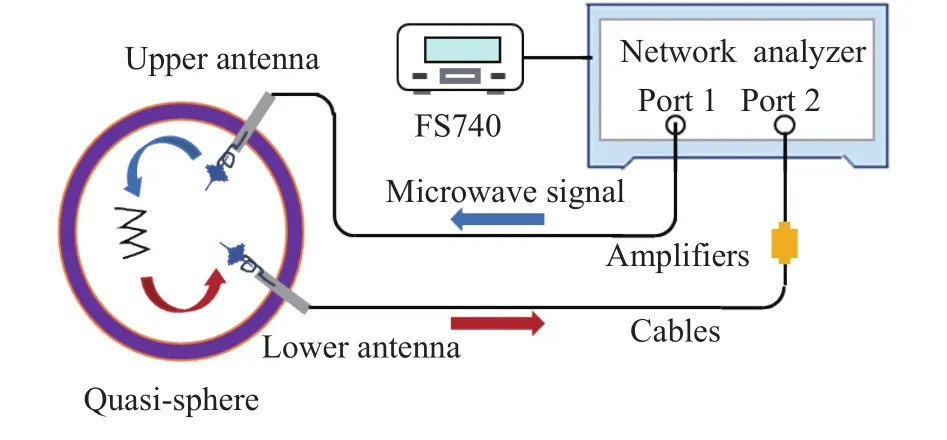
图1 微波谐振频率测量示意图Fig.1 The schematic of the microwave resonance frequency measurement

微波谐振频率和半宽度通过拟合源频率f和复数散射参数S21确定，拟合式如公式(1)所示[25]，拟合方法为Levenberg–Marquardt方法.

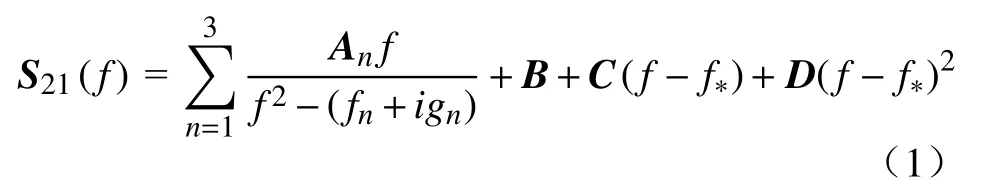
其中，n=1、2、3分别代表x、y、z方向，An、B、C、D为待拟合的复常数，fn是每个共振峰的中心频率，gn是半宽度，变量f*是所设置的任意频率，本文中f*=f2.

实际实验中，腔体材料的非完美导电性、波导效应（天线孔、进出气孔）、形状效应等因素会使共振频率偏离其理想值，因而需要进行非理想修正[21−25].由于加工技术及加工精度所限，不能制造出完美球形，加工出的球形谐振腔会出现微波缔合现象，难以获得高品质值共振频率，导致谐振频率测量精度大幅下降.针对这个特点，选择采用可以分离微波缔合模式的准球形谐振腔.真空状态下，准球形谐振腔的半径R可通过测量微波谐振频率由公式(2)计算确定[9]：

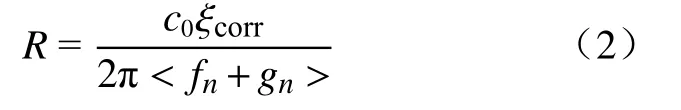
其中，c0是真空光速，ξcorr是形状修正后的特征根[24]，是半宽度修正后的平均微波谐振频率.

1.2 准球形谐振腔

准球形谐振腔是完美球腔的一个微扰结构，其在三维空间x、y、z方向上的半径具有适当的差异，以实现微波频谱缔和的有效分离，可将微波谐振频率测量准确度提升3个数量级[25]，广泛应用于基准测温领域[2−6].

谐振腔材料为经电解精炼后的Cu-ETP，具有很好的导热性，更容易确保低温温度的均匀性[26].由于制造工艺的限制，每个准球形谐振腔由两个需组装的半球组成，为了减少微波损耗，上、下半球的内表面采用精密钻石刀抛光.我们采用相对过量半宽度监测方法，实现了两个半球的精准闭合[27]，保证了微波谐振频率的高精度测量.

准球形谐振腔内表面可由公式(3)表示：

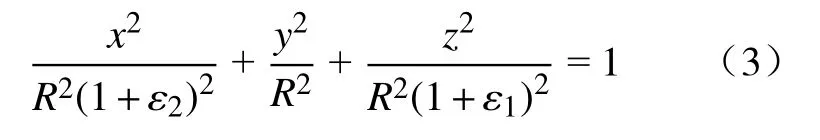
其中，R=50.00 mm是准球腔在y轴方向的半径，ε1=0.001和ε2=0.0005分别是z轴和x轴的形状参数，壳体设计厚度为10.0 mm.准球形谐振腔详细结构和参数参见文献[4].

1.3 线性热膨胀系数计算方法

线性热膨胀系数α表示的是温度T改变1 K时固态物质长度l的相对变化，其定义如公式(4)所示.

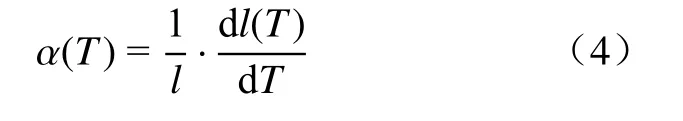
长度l对温度T的导数通过以下方法确定：首先将长度拟合为温度的一个合适的多项式函数，如公式(5)所示；然后，再对温度求导获得长度对温度的导数，如公式(6)所示.

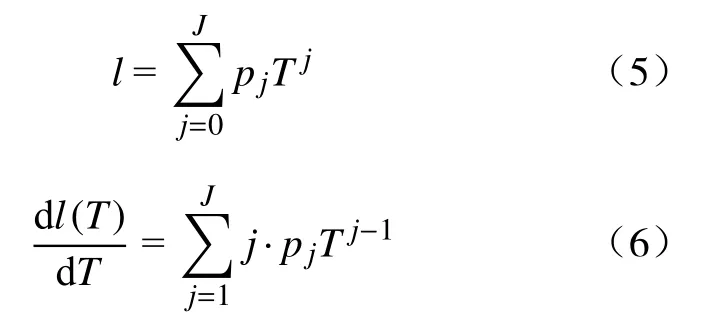
其中，J为多项式拟合的阶数，pj为待拟合的多项式系数.

除特别说明外，本文中的所有温度值均是指1990年国际温标（ITS-90）[28]框架下的温度值.

1.4 不确定度分析方法

除非另有说明，本工作中的所有不确定度均为标准不确定度，置信因子为k=1，对应于68%的置信区间.如公式(4)所示，热膨胀系数是由长度值随温度的变化关系经求导得出，因此，进行热膨胀系数的不确定度分析的前提是已知长度的不确定度，本文中长度均指代谐振腔半径值.下面首先介绍半径值的不确定度分析方法.

1.4.1 半径不确定度计算

准球形谐振腔的半径值计算如公式(2)所示，主要与微波谐振频率和修正后的特征根有关，从这两个角度对半径进行不确定度分析，计算方法如公式(7)所示.微波谐振频率是由微波信号按照公式(1)进行频率扫描和拟合得到，会存在拟合不确定度，即Levenberg–Marquardt方法的拟合精度，如公式(7)中的第一项u(ffit)所示；每个数据点的结果是通过多次扫频取平均得到，每次扫频的微波谐振频率会有细微差异，影响最终半径值的计算，因此存在频率稳定性这个影响因素，等效为多组微波谐振频率频率数据的标准差，如公式(7)中的第二项u(fstability)所示；公式(2)中的特征根是指经过非理想因素修正后的特征根，表征了实际和理论测量的差异，非理想修正的考虑与否也会影响半径的测量，如公式(7)中的第三项u(fnon-ideal)所示.在进行微波谐振频率测量时，根据初始扫频的不同，最终采集了多个微波模式的频率数据，各微波模式的测量结果之间存在偏差，需要比较各微波模式频率数据计算得出的半径差，即微波模式一致性，控温过程等效为各微波模式计算结果的标准差，降温过程中由于温度变化快，先进行温度修正后作标准差，为公式(7)中的第四项u(Rmode)；为减小随机误差的影响，测量过程中均进行了多轮独立测量，各轮测量结果间存在差异，与模式一致性分析方法相同，也是对所采集的多轮数据先进行温度修正后对所得多轮新数据作标准差作为数据的重复性，如公式(7)中的第五项u(RRun repeability)所示.

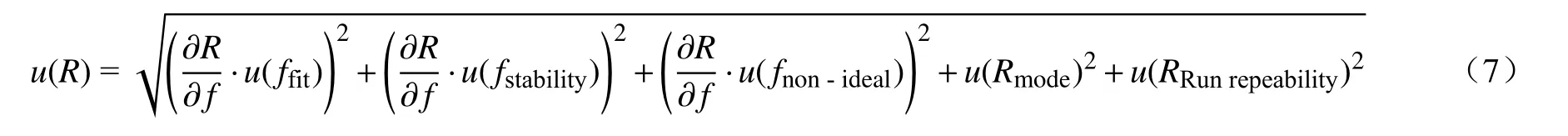
1.4.2 热膨胀系数不确定度计算

该系统中的热膨胀系数是对半径值随温度的变化关系经求导得出，而在联立半径值随温度的变化关系时，受限于测量仪器的采样周期，所采集的数据是覆盖整个温区的温度散点.因此，需要将所采集的半径和温度数据进行多项式拟合，得到半径和温度的确切关系后，对其进行拟合从而得到热膨胀系数值.半径与温度的拟合程度对于热膨胀系数的计算至关重要，通过比较对半径值增加一个半径不确定度和原半径值算出的热膨胀系数值，从而确定半径拟合不确定度，如公式(8)中的最后一项偏导数乘u(Rfit)所示.其他不确定度影响因素同上，计算方法与半径拟合相同，均为比较对半径值增加一个各分量的不确定度和原半径值算出的热膨胀系数的差异得到，最终不确定度分析方法如公式(8)所示，其中，前三项与半径不确定度计算时的表达意义相同，而热膨胀系数的计算中同样会采用不同的微波模式频率数据进行计算，同样会有微波模式一致性，这里表示为u(αmode)；与半径不确定度分析方法相同，也是对所采集的多轮数据先进行温度修正后对所得多轮新数据作标准差作为数据的重复性，如公式(8)中的第五项u(αRun repeability)所示.

2 实验

2.1 实验系统

图2为定压气体折射率基准测温系统示意图[29]，也是Cu-ETP线性热膨胀系数测量实验系统图，该恒温器由脉冲管制冷机（Sumitomo RP-082B2）提供冷源，可以在4.2 K提供约1 W的冷量.为了获得更低的工作温度，采用了多级防辐射屏和柔性热连接件，结合气体热开关，可将准球形谐振腔的温度最低降至4.3 K[30].每级法兰上都布置有Cernox温度计，以监控温度的变化.为获得高稳定的测量环境，控温过程中，使用Cernox 1050型温度计T2组合8½ Keithley 2002数字多用表对二级法兰进行控温、采用一支经英国国家物理实验室（NPL）校准的标准铑铁温度计（Tinsley，SN 226245，下文简称为NPL2）配合AC交流电桥（ASL F18）对压力腔进行联合控温，最终，实现了谐振腔温度的μK量级高稳定性控制[31].受温度计标定范围所限，降温过程中采用序列号为X118726的CX-1050-CU-HT-1.4L型Cernox温度计T10进行降温过程中谐振腔温度采集，控温过程中采用另一支经NPL校准的标准铑铁温度计（Tinsley，SN 226242，下文简称为NPL1）进行控温过程中谐振腔温度采集，各温度计的布置如图2所示.通过采用多重筒体和防辐射屏及在温度计表面进行绝热、防辐射处理，减少与外界环境的影响，确保装置内部测温环境的独立与准确，该装置中涉及到的测量仪器具体信息及其精度如下表1所示.

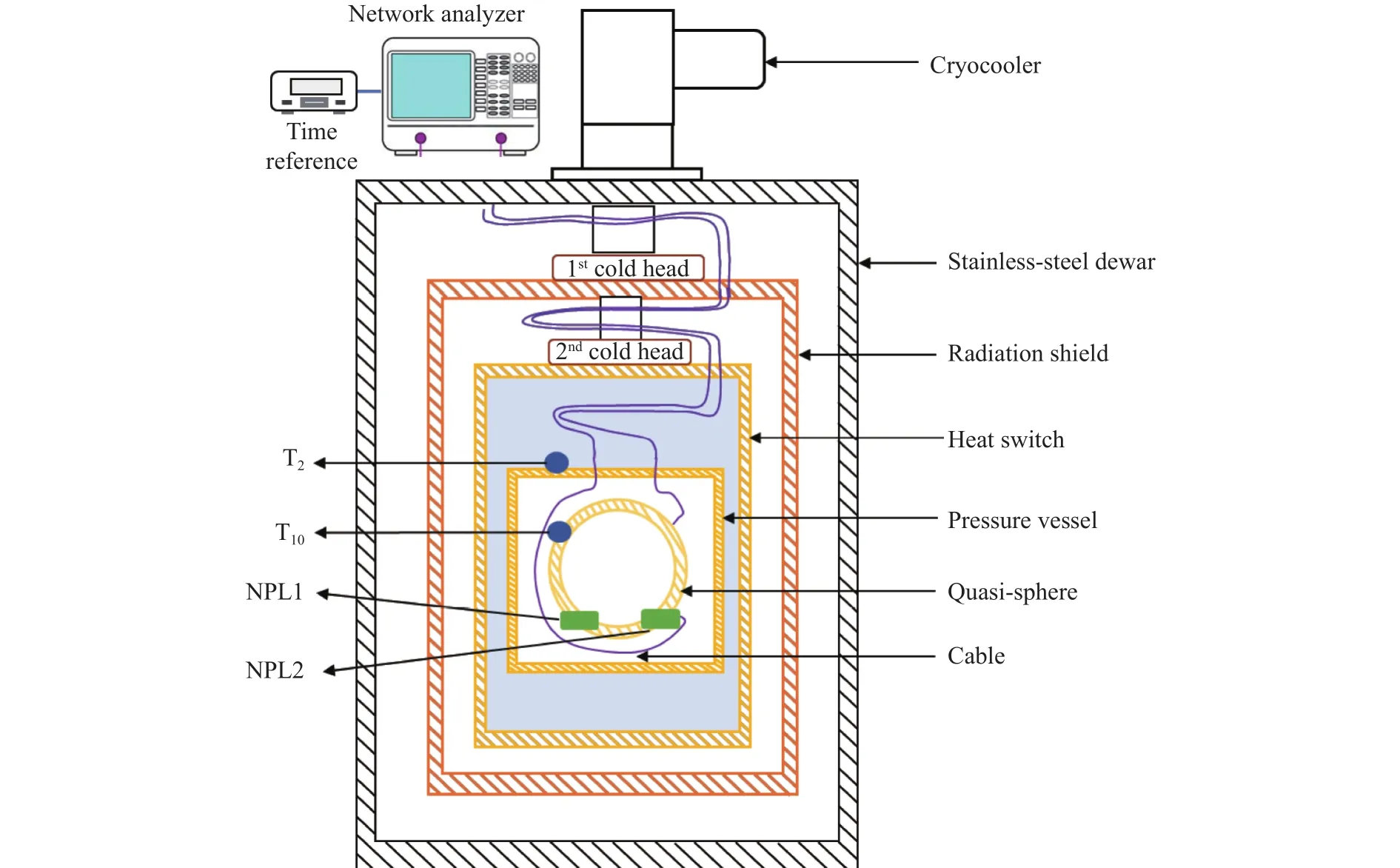
图2 线性热膨胀系数测量实验系统图Fig.2 The schematic of the linear thermal expansion experiment system

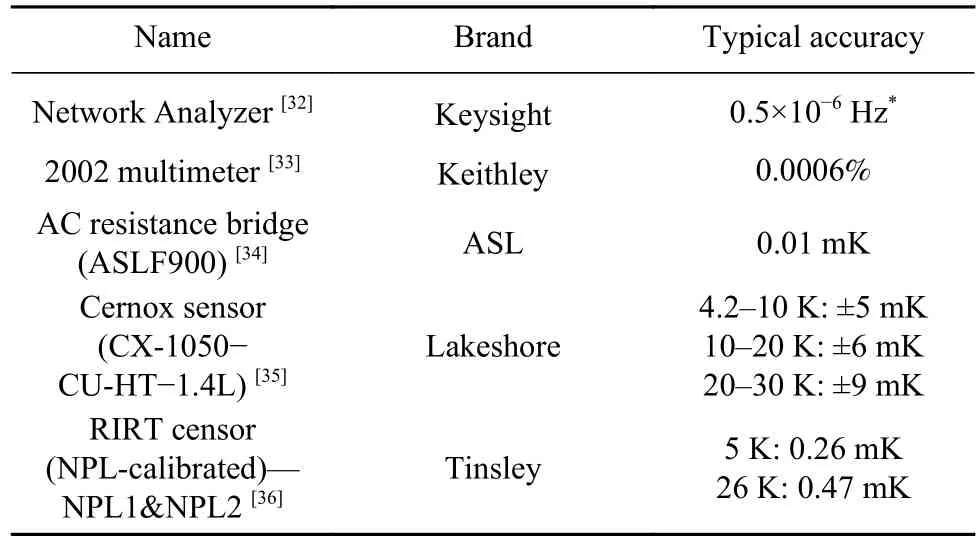
表1 本装置中的仪表信息Table 1 Instrument information in this cryostat

2.2 实验步骤

本文中微波谐振频率测量采用降温法（动态法）和控温法（静态法）两种实验测量方案.方案1：需要将整个恒温器从室温降温到低温并同时进行微波谐振频率采集；方案2：将准球形谐振腔降温到目标温度，并进行单个点的温度控制和微波谐振频率采集.

具体步骤如下：

(1) 记录系统中各个温度计的读数温度T.动态法中，谐振腔温度值由T10-Cernox温度计进行测量；静态法中，谐振腔温度值由NPL1标准铑铁电阻温度计确定，其由英国国家物理实验室标定，详见文献[36]第三章节部分.

(2) 微波发射功率为−10 dBm，多个微波模式下的S21数据按照微波谐振频率由低到高连续循环采集（比如，“TM11—TE11—TM12—TE13”，TM为横磁模式，TE为横电模式，后面的数字为区分的微波谐振频率范围）.动态测量时，谐振腔温度变化快，为实时响应温度变化、保证微波谐振频率拟合结果收敛，应加快频率扫描速度，扫描带宽设为50 Hz；静态测量时，为降低微波测量噪声，提高微波谐振频率测量精度，应降低频率扫描速度，扫描带宽设为5 Hz.

(3) 采用公式(1)实时拟合散射参数，并记录相应微波模式的微波谐振频率、半宽度等数据.对于静态法，完成一个目标温度的测量后，需重复上述相应测控过程，直到覆盖整个研究温区（4.3～26 K）.

为了检验系统的可靠性，本文中我们采用两种实验方案开展了多轮独立重复实验.

3 实验结果

3.1 降温实验结果

为了消除随机误差的影响，得到可靠的结论，我们多次重复了降温过程并进行计算，为了使整个实验装置降温到最低温度，需要在降温过程开始之前向实验装置中添加氦−4气体，如图2中蓝色部分所示.而所充入氦−4气体的量会影响降温速度，本文中研究的不同轮实验的降温过程如图3所示，可以看到从室温299 K到5 K的降温过程持续约30 h，具体时间由室温起始温度和所充入氦−4气体的量决定，当起始充入的氦−4气体越多时，实验装置降温越快.图中红线为Run12轮（第12次）实验，此时的降温过程中水冷机发生了短暂暂停后并重启，因此如图中所示重启后的降温速率有所减慢.Run9到Run17之间图中没有的其他轮（Run11、Run13～Run16）实验由于停电导致制冷机停机、降温中断，未传输、保存温度数据，降温过快导致个别微波模式数据不收敛等原因，在降温过程中均未采集完整、有效的降温数据，为此，本文中研究了如下四轮（Run9、Run10、Run12、Run17）降温数据.

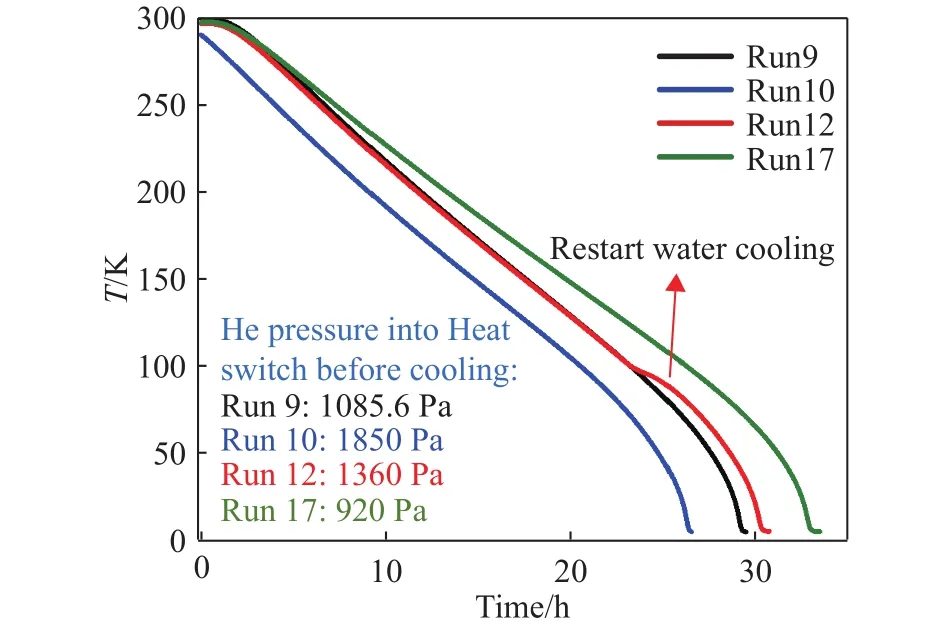
图3 各轮实验的降温过程Fig.3 The cooling procedure of different runs

3.1.1 谐振腔半径

在降温过程中，微波谐振腔的温度由Cernox低温电阻温度计（T10）采集，低温下该温度计具有灵敏度高和稳定性良好的优点，其测量不确定度详见其官方网站[35].按2.2章节实验方案，通过微波谐振频率测量，由公式(2)可得到降温过程中不同微波模式测得的微波谐振腔体半径.

图4为微波谐振腔半径的实验测量结果.其中，图4(a)描绘了Run9降温过程中不同微波模式计算的半径Rmode随温度的变化；并且，获得了不同微波模式半径计算值与第9轮平均值RRun9,avg的偏差，如图4(b)所示，最大偏差为0.37 μm，表明半径测量结果具有良好的微波模式一致性.

进一步，为考察半径测量的重复性，我们在长达两年零三个月的时间内进行了四轮独立降温实验（Run9、Run10、Run12、Run17），实验结果如图4(c)所示，可以看出，各轮半径测量值RRun,avg与四轮结果平均值Ravg之间的偏差均在Ravg的测量不确定度内，多次独立降温实验结果具有良好的重复性.

最后，我们将各次实验平均半径RRun,avg的平均值Ravg作为最终的测量半径值，图4(d)所示为半径Ravg测量标准不确定度u(Ravg)的分析结果.在整个测量温度范围内，半径测量的标准不确定度u(RTotal)小于0.27 μm，其最大的不确定度源自不同微波模式测量半径结果的一致性.在150 K～299 K之间，半径测量结果的重复性是其第二大来源，主要是由于四次独立实验的开机降温条件不同（室温温度、系统真空、热开关充气压力等参数），导致该温度区间降温速率不同；低于150 K的温度区间内，微波测量的非理想性超过半径测量重复性成为其第二大不确定度来源，可以看出，低温区半径测量结果几乎不受室温端开机实验条件的影响，从而更利于实现高准确度的半径测量.

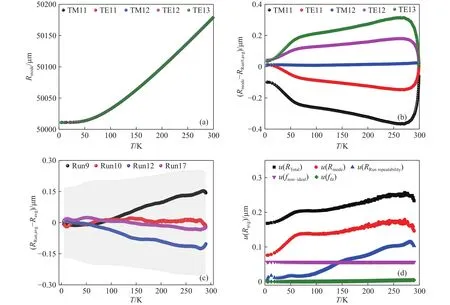
图4 降温过程中的谐振腔半径计算结果分析.(a) Run9单个微波模式测得的半径; (b) Run9单个微波模式测得的半径与平均半径的偏差; (c) 不同轮实验测得的半径平均值与最终半径平均值的偏差(灰色背景为半径平均值的标准不确定度误差带); (d) 降温过程中最终半径平均值的不确定度分析Fig.4 Analysis of the resonator radius during cooling: (a) radius of each microwave mode of Run9; (b) deviation of the single microwave mode and the average radius of Run9; (c) radius deviation in different runs and the average value (the gray background is the error bar of the standard uncertainty in the average radius value); (d) uncertainty analysis of the final average radius during cooling

3.1.2 线性热膨胀系数

为了降低拟合公式(5)的残差影响、获得合适的拟合阶数，我们采用不同的多项式阶数进行了拟合，拟合结果Rfitting与实验结果Rexperiment之间的对比结果如图5所示.其中，图5(a)为选取拟合阶数J为7到12时谐振腔半径的拟合残差，图5(b)为不同拟合阶数对应的残差标准差，当拟合阶数J=9时，残差小于半径测量不确定度且残差标准差不再随拟合阶数的增加而大幅变化，可满足计算要求.因此，在后续降温过程线性热膨胀系数的计算中，选取拟合阶数Jopt=9.

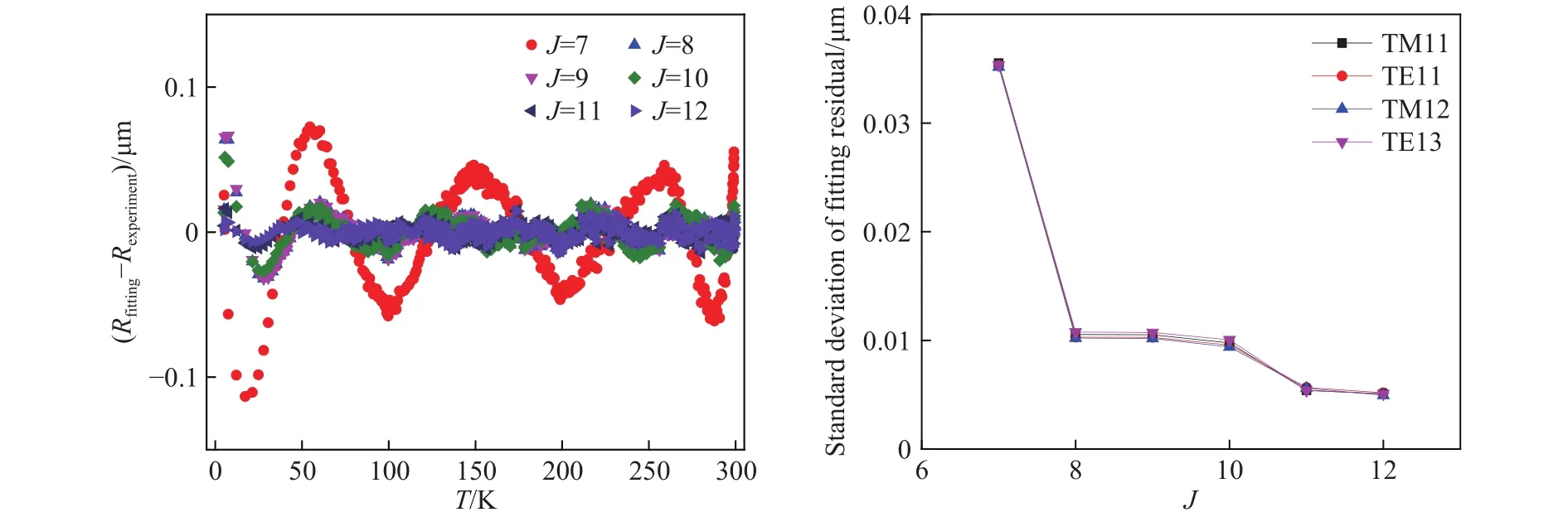
图5 不同拟合阶数的拟合结果.(a) 不同拟合阶数下半径实验值与拟合值相对偏差的变化; (b) 不同拟合阶数下拟合残差标准差的变化Fig.5 Fitting result of different fitting sequences: (a) deviation of the experimental and fitting values of the radius with different fitting order; (b) change of standard deviation of the fitting residual with different fitting order

图6为降温过程中测得的5～299 K的Cu-ETP线性热膨胀系数结果.其中，图6(a)为Run9不同微波模式计算结果αmode与文献[7]中高导无氧铜线性热膨胀系数数据αNIST（其中高导无氧铜热线性膨胀系数的关联方程适用范围为4 K≤T≤300 K，计算不确定度为 1.4×10−7K−1）的对比结果，可以看出，两者偏差几乎全部在文献计算结果的标准不确定度内，最大偏差仅为 1.6×10−7K−1，且不同微波模式的线性热膨胀系数实验结果具有良好的一致性.

进一步，基于四次独立降温实验，获得了线性热膨胀系数实验测量的重复性结果.图6(b)呈现了不同轮实验线性热膨胀系数平均值αRun,avg与多轮实验结果最终平均值αavg的偏差在5～299 K温度范围内的变化趋势.可以看出，室温附近不同轮实验结果的偏差较大，主要是由于四次独立实验的开机降温条件不同，导致室温至270 K温度范围内降温速率不同；在低于25 K的温区内，偏差再次变大，主要是因为低温下谐振腔比热变小，降温速度变快，可采集的实验数据点较少导致，这也说明了有必要采用控温法对该温区的线性热膨胀系数进行实验测量.整体而言，5～299 K温度范围内αRun,avg与αavg的偏差均小于 1.9×10−7K−1，这表明降温数据具有良好的重复性，结果可靠.

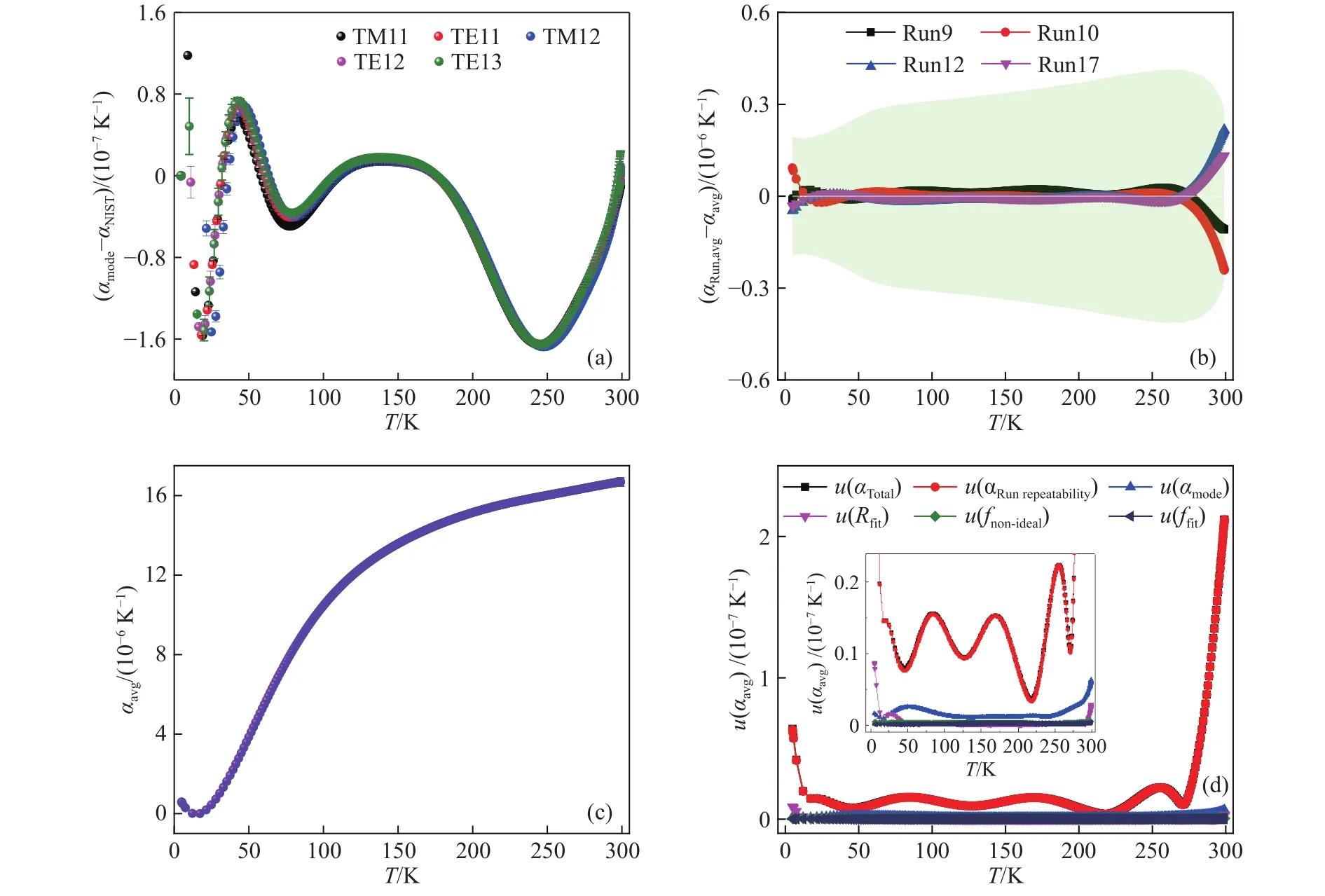
图6 Run9降温过程中线性热膨胀系数计算结果分析.(a) 各微波模式线性热膨胀系数计算值和文献值的偏差; (b) 不同轮实验线性热膨胀系数平均值与最终平均值的偏差; (c) 不同轮线性热膨胀系数的最终平均值; (d) 线性热膨胀系数的不确定度分析Fig.6 Analysis of the linear thermal expansion during the cooling of Run9: (a) deviation of linear thermal expansion of every microwave mode and the literature value; (b) deviation of the linear thermal expansions of different runs and the final average value; (c) final average value of the linear thermal expansion of different runs; (d) uncertainty analysis of the linear thermal expansion

最后，我们将各次实验αRun,avg取平均获得了线性热膨胀系数αavg，αavg及其标准不确定度u(αTotal)随温度的变化分别如图6(c)和图6(d)所示.可以看出重复性是影响不确定度的最主要来源，其影响比其他各分项大2到3个数量级，并且在270 K以上和24.5 K以下影响更大，这是由于刚开始降温时的降温速率很快，而低温下由于降温很缓慢，可采集的有效数据点数比较少；微波模式一致性是重复性以外的第二大影响因素，刚开始降温时和24.5 K以下的影响也比较大，因此，开展后续控温过程中的线性热膨胀系数计算很有必要，降温过程线性热膨胀系数最大标准不确定度为2.2×10−7K−1.

3.2 控温实验结果

3.2.1 谐振腔半径

受基准测温装置中制冷机冷量参数和加热器的功率峰值限制，目前低温区可控的温度范围为4.3～26 K，因此，在控温过程中主要开展此温度区间的热膨胀系数测量研究.同降温过程分析方法，图7(a)为Run10控温法各个微波模式测量的微波谐振腔半径Rmode结果，图7(b)为Run10各个微波模式测得的半径Rmode与Run10平均半径RRun10,avg之间的偏差.可以看出，不同微波模式测得的半径Rmode随温度的变化趋势并不完全相同，TE11模式的半径与RRun10,avg的偏差最小，而TM11模式的半径与RRun10,avg的偏差最大，在4.3～26 K温度范围内，四种微波模式半径与RRun10,avg的偏差量级是相同的，最大变化幅度为0.089 μm，半径测量结果具有良好的微波模式一致性.

图7(c)为多次独立重复实验中各微波模式的平均半径值RRun,avg与其最终平均值Ravg的偏差结果（其中，Run9实验在不拆机的情况下进行了两轮实验，分别表示为Run9-1和Run9-2如图中图例所示），偏差均在0.0056 μm内，小于半径测量标准不确定度u(Ravg)，具有良好的重复性.与降温法半径测量结果相比，控温法半径测量结果的重复性提升约2倍，主要是因为多个微波模式连续循环采集存在时间差，降温时各微波模式温度不一致引起.

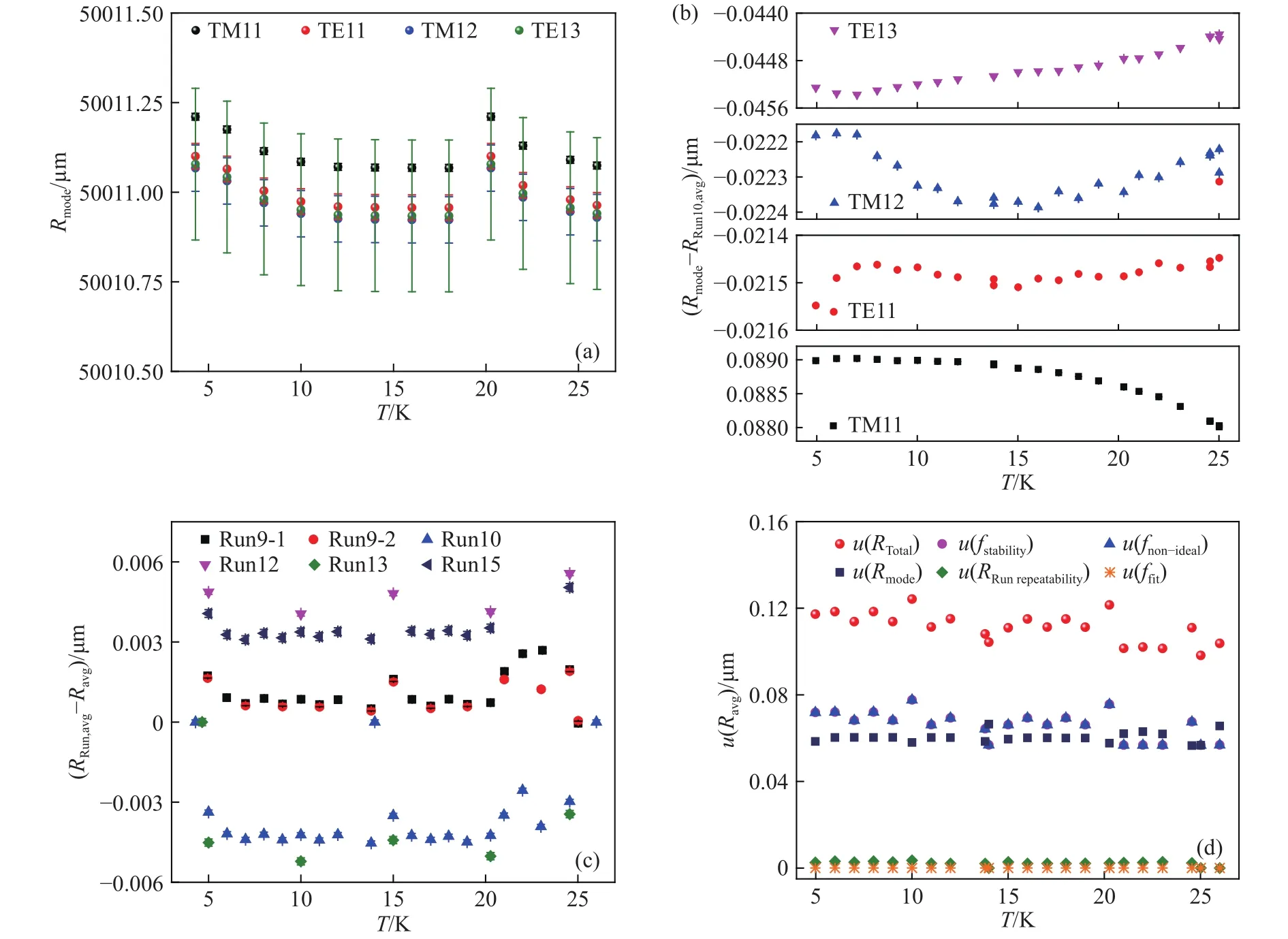
图7 控温过程中谐振腔半径计算结果分析.(a) Run10控温过程中各微波模式谐振腔半径计算结果; (b) Run10控温过程单个微波模式半径和平均半径的偏差; (c) 各轮控温过程中半径各模式平均值和最终平均半径值的偏差; (d) 控温过程中半径的不确定度分析Fig.7 Analysis of the resonator radius during temperature control: (a) resonator radii of different microwave modes in Run10; (b) deviation of single microwave mode and average radius in Run10; (c) deviation of the average radii of different modes in different runs and the final average value; (d)uncertainty analysis of the resonator radius

最后，我们将各次实验平均半径RRun,avg的平均值Ravg作为最终的测量半径值，其不确定度分析u(Ravg)及不确定度分量占比如图7(d)所示.可以看出，Ravg的合成标准不确定度u(RTotal)约为0.12 μm，这里列出了五个主要的不确定度分量.其中，非理想修正和频率稳定性是两个主要因素，占比近乎相同；其次，微波模式一致性的影响比上述两个分量小，但它们对半径的影响在同一量级；而半径测量重复性和频率拟合的影响很小，与其他三个因素相比可以忽略不计.为了更清楚地了解每个分量的占比，在表2中详细列出了半径Ravg在5、15和24.5 K时的标准不确定度结果.

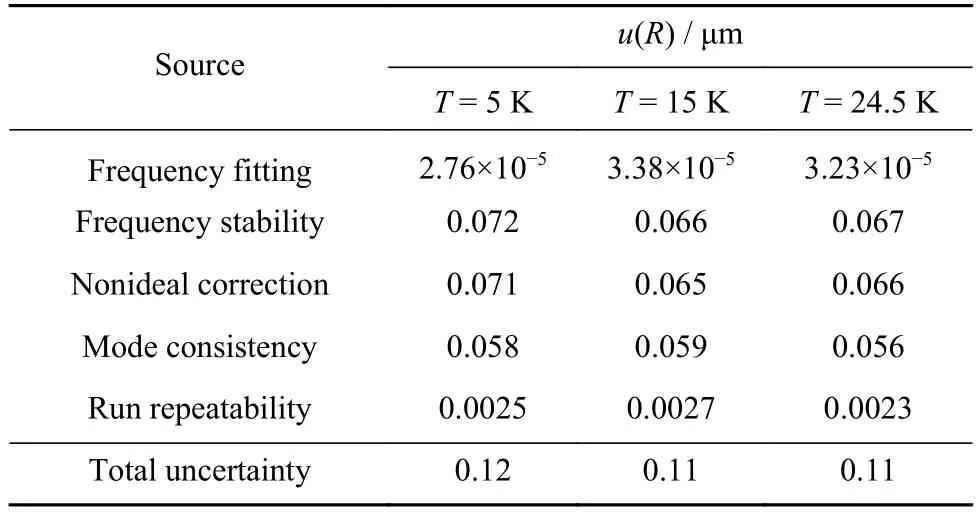
表2 5、15和24.5 K下准球形谐振腔半径的不确定度分析Table 2 Uncertainty analysis of the radius at 5, 15, and 24.5 K

3.2.2 线性热膨胀系数

我们首先对整个温区每个微波模式测得的半径数据作多项式拟合，与降温法分析思路一样，根据拟合残差、残差标准以及半径测量标准不确定度，确定最佳的多项式拟合阶数为Jopt=7，此时，拟合残差的影响相对测量半径的不确定度可以忽略不计.

4.3～26 K温区Cu-ETP线性热膨胀系数结果如图8所示.图8(a)为Run10各微波模式实验测量值αmode和文献值αNIST[9]的比较结果.在图8(a)所示的整个温度范围内，各微波模式线性热膨胀系数结果与文献值的偏差在2.1×10−8K−1范围内，比降温实验结果（图6(a)）小一个数量级，表明控温法测量结果具有更好的微波模式一致性.

图8(b)呈现了不同轮实验线性热膨胀系数各微波模式平均值αRun,avg与多轮实验最终平均值αavg的偏差在4.3～26 K温度范围内的变化趋势.可以看出，整个测量范围内αRun,avg与αavg的偏差小于 2.8×10−9K−1，这一结果比降温法小一个数量级，再次表明控温法测量结果具有更好的重复性.

图8(c)和图8(d)分别为各轮实验αRun,avg的平均值αavg及其标准不确定度u(αTotal)的分析结果，控温过程中线性热膨胀系数的最大标准不确定度为 2.9×10−9K−1.线性热膨胀系数测量不确定度的来源主要有两类：含有非理想修正的谐振频率的实验测量和多微波模式频率测量.在第一类中，主要包括由腔体非理想性导致的趋肤效应[37]，由气体管道和天线探针孔洞引起的波导修正[37]，准球腔特殊设计形状的二阶形状修正[38−39]以及基于相同温度分析的温度修正.第二类是多轮独立实验，多微波模式谐振频率测量等引入的不确定度.其最大的测量不确定度来源为多模式微波测量结果的一致性；其次，是多次独立实验的重复性，相比这两个因素，其他不确定度来源的影响可以忽略不计，表3中列举了5、15和24.5 K的αavg标准不确定度分析结果.

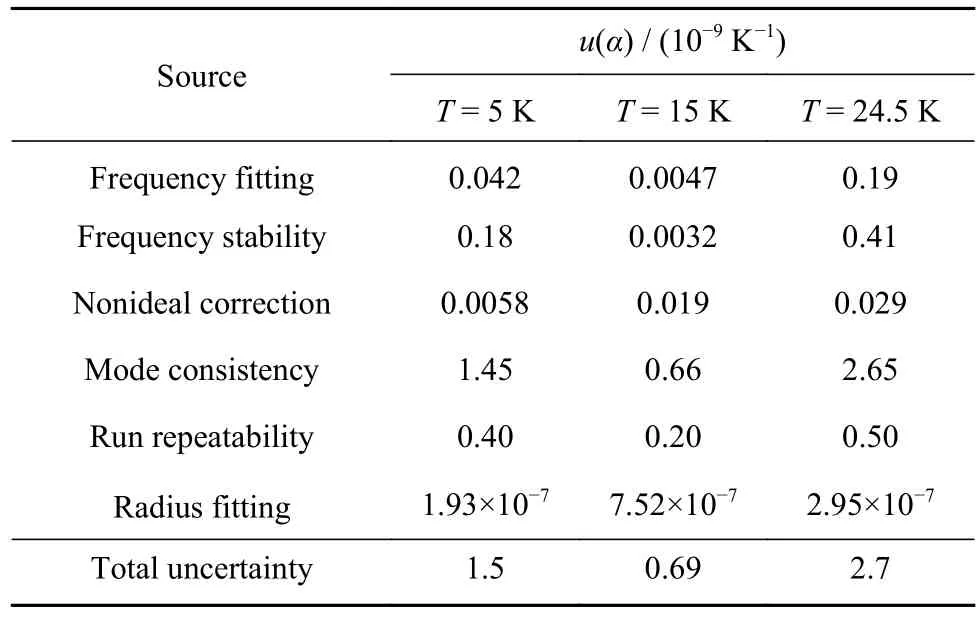
表3 5、15和24.5 K下线性热膨胀系数不确定度分析Table 3 Uncertainty analysis of linear thermal expansion at 5, 15, and 24.5 K

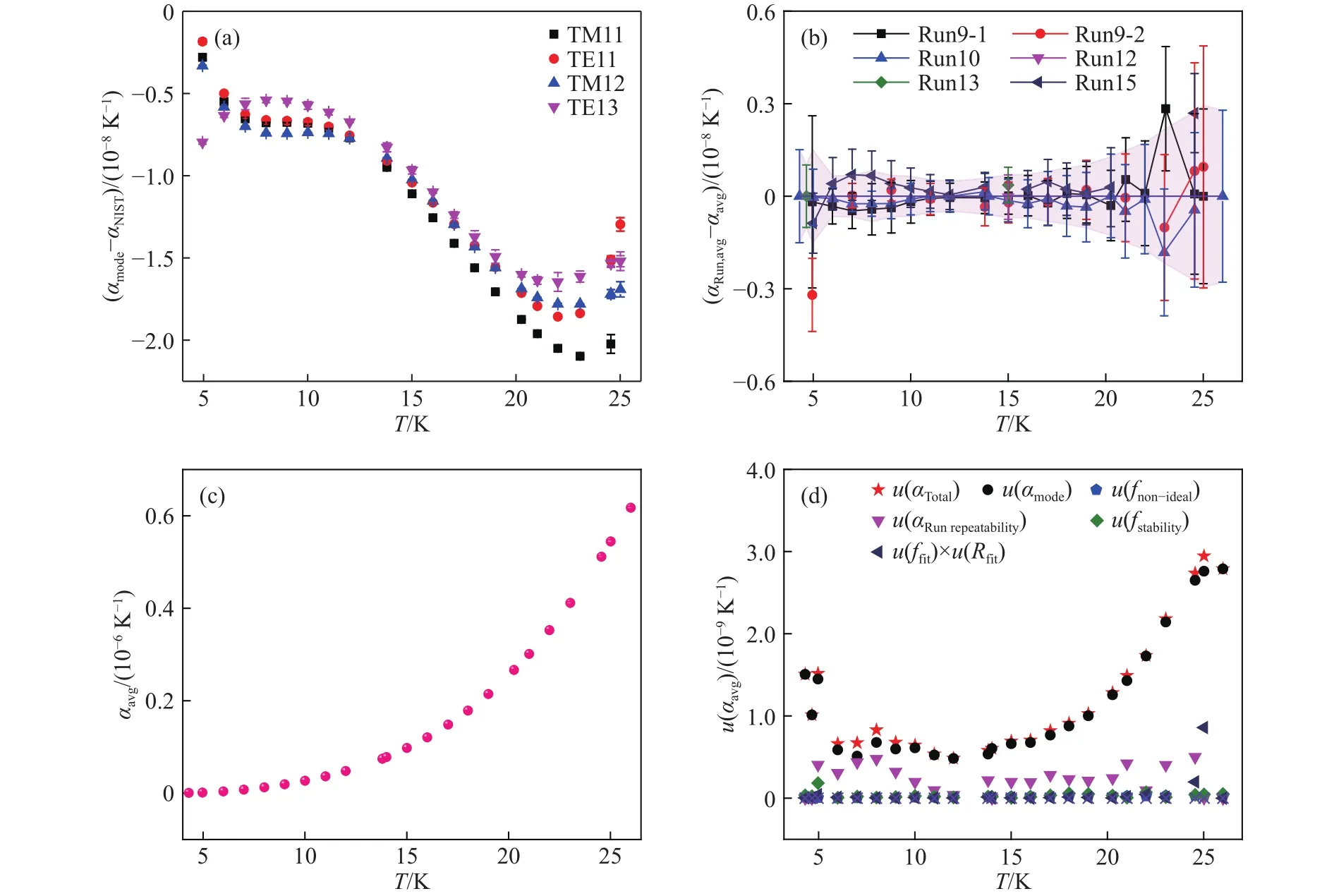
图8 控温过程中线性热膨胀系数计算结果分析.(a) Run10实验中各微波模式线性热膨胀系数计算结果与文献值的偏差; (b) 不同轮实验线性热膨胀系数平均值和最终平均值的偏差(粉色背景为平均值的标准不确定度误差带); (c) 多轮控温过程中线性热膨胀系数的最终平均值; (d) 控温过程中线性热膨胀系数的不确定度分量占比Fig.8 Analysis of the linear thermal expansion during temperature control: (a) deviation of experiment and reported linear thermal expansion of Run10 for microwave different modes; (b) deviation of average thermal expansion for different runs and the final average value (the pink background is the error bar of the standard uncertainty of the final average value); (c) final average value of linear thermal expansion for different runs; (d) uncertainty analysis of the final linear thermal expansion

3.3 线性热膨胀系数关联方程

在3.1和3.2章节中，我们基于多轮、多微波模式实验测量获得了定压气体折射率基准测温系统中Cu-ETP线性热膨胀系数，为便于应用，我们将所测得的线性热膨胀系数平均值αavg及其标准不确定度u(αavg)关联为温度的多项式函数，最佳的多项式阶数值Jopt的确定与上述章节中半径拟合时相同，这里不在赘述.为便于公式推广于适用于一般情况，本章节中下标αavg表示为α.

降温法5～299 K线性热膨胀系数α及其标准不确定度u(α)与温度的的拟合函数α(T)和u(α(T))分别为：

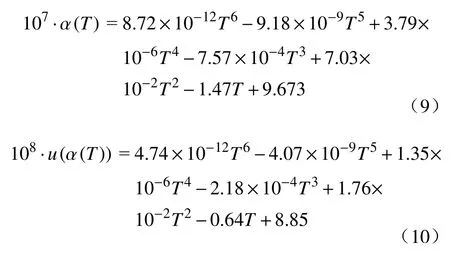
其中，公式(9)拟合残差的标准不确定度为3.3×10−8K−1，小于实验标准不确定度u(α)，公式 (9)拟合残差影响可以忽略不计；公式(10)计算的残差仅为实验标准不确定度u(α)的2.2%，具有很好的复现性.

控温法4.3～26 K线性热膨胀系数α及其标准不确定度u(α)的拟合函数α(T)和u(α(T))分别为：

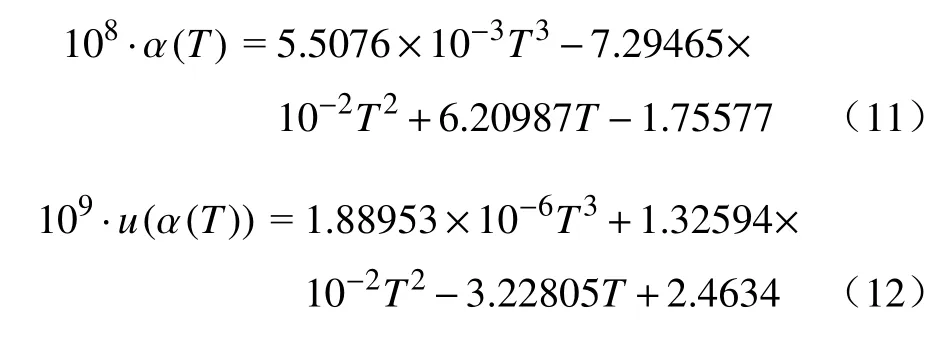
公式(11)的拟合残差的标准不确定度为4.1×10−10K−1，实验标准不确定度与温度的关系如公式(12)所示，由于4.3～26 K控温法测量结果更优，实际使用时在4.3～26 K温度区间内建议采用公式(11)进行计算，26～299 K温度区间内建议采用公式(9)进行计算.

上述方程不仅可以用于等温压缩系数和热力学温度的计算，还可以用于真空实验数据预处理，不同温度下微波谐振频率可由公式(13)相互转换.在真空实验中，如果在计划之外缺少了某个实验状态的微波谐振频率，我们就可以利用公式(13)结合线性热膨胀系数关联方程α(T)计算获得.

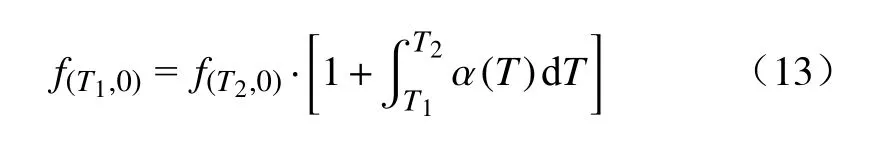
式中，f(T1,0)和f(T2,0)分别为真空状态下温度为T1和T2时所测得的微波谐振频率.

4 结论

基于多模式微波谐振法，本文原位测量了定压气体折射率基准测温系统中Cu-ETP线性热膨胀系数，采用降温法和控温法两种实验测量方法，获得了4.3～299 K范围内一组完整、高精度的Cu-ETP热膨胀系数数据.

降温法（5～299 K）线性热膨胀系数测量标准不确定度为 2.2×10−7K−1，其中，重复性是其测量不确定度的主要来源，室温区不确定度较大主要是由于重复实验的开机条件不同引起.控温法（4.3～26 K）线性热膨胀系数的测量标准不确定度为2.9×10−9K−1，其中，微波模式一致性和重复性是其测量不确定度的两大主要来源.这两种测量方法都采集了多个微波模式数据，计算结果也反映了良好的微波模式一致性.控温稳定性高、微波测量噪声低，控温法获得的线性热膨胀系数结果更为精确，与降温法相比，不确定度约小两个数量级，控温法更适用于高精度线性热膨胀系数的实验测量.

最终，发展了定压气体折射率基准测温系统中Cu-ETP材料的线性热膨胀系数方程，实现了线性热膨胀系数与温度的高精度关联，可用于低温计量领域等温压缩系数等物性测量计算、微波谐振频率测量的准确性检验以及真空条件下不同温度微波谐振频率的修正计算.