基于实测数据的多类型电动汽车充电负荷分析

蒋林洳，龙羿，李兴源，张元星，陈中

(1.中国电力科学研究院有限公司用电与能效研究所检测中心(北京市电动汽车充换电工程技术研究中心)，北京 100192； 2.国网重庆市电力公司营销服务中心，重庆 401123； 3.东南大学 电气工程学院，南京 210096)

0 引 言

自2012年制定《节能与新能源汽车发展规划(2011年～2020年)》后，我国电动汽车市场进入自主品牌快速发展的新阶段。2015年，我国新能源汽车累计产销突破50 万辆，对全球市场的贡献超过一半。2016年我国电动汽车的保有量达到109 万辆，已成为全球规模最大的新能源汽车制造国[1-2]。

考虑到其经济性及环境保护作用，电动汽车将成为未来各国经济增长的重要组成部分[3-4]，分析电动汽车用车行为，有利于电动汽车负荷预测以及有序充电策略的制定等。文献[5-6]从新能源汽车的发展历程切入，将2019年政府补贴下降的不利影响做了部分归纳，同时指出税收优惠等配套政策将给产业带来新的动力；文献[7-10]借助相关数学模型，对国外电动汽车用户出行行为进行研究，其中John G等人将Nissan LEAF电动汽车作为研究对象，进一步探讨了用户的充电行为特征；文献[11]采用探索性空间数据分析(ESDA)技术对上海市的出租汽车统计信息进行分析，利用莫伦值(Moran’s I)进行评估，表明出租汽车出行具有较强的空间正相关性，与中心商业区的活动高度相关，时空结构稳定；文献[12]对共享汽车这一新型出行方式进行了初步分析，基于EVCARD公司的订单数据，借助描述性统计量分析用户通勤时段出行特征；文献[13]利用数据挖掘等方法，分析了城市级物流电动汽车充电行为规律，得到了服从正态分布的充电前后SOC模型，为用户的出行策略提供科学支持；文献[14]采用聚类法，研究了共享汽车用户行为与企业利润间的关系，并借助多层感知神经网络对不同用户进行了分类预测；文献[15]基于蒙特利尔地区用户的用车数据，采用数据挖掘等方法按用户特征进行群体分类；文献[16]建立了数据驱动的线性回归模型，分析得出停车位的数量是影响用户出行的首要因素；文献[17]结合地理信息对电动汽车订单数据进行时空特性分析，利用线性回归的方法对订单量进行预测。

随着电动汽车行业发展，其带来的居民出行模式改变问题不容忽视，将成为城市交通领域的热点问题，探讨不同电动汽车车型的出行规律具有较高研究价值。基于实测用户订单数据，对某地2018年12月1日～12月30日的电动汽车数据进行分析，得到公交车、运输车、私家车、租赁车四种车型的出行预测规律，并采用蒙特卡洛法对区域电动汽车负荷进行建模预测。

1 数据预处理

1.1 数据采集格式

截止目前，采用的平台数据库存储了从2018年12月1日～2018年12月30日共计1 656 776条电动汽车数据，时间跨度为30天。筛选出其中数量较多的车型，最终得到1 541 923条初选数据，源数据保留率为93.07%。每条数据包含了用户的多维用车行为信息，包括车型、采集时间、车辆SOC、里程数以及行驶速度(见表1)。

表1 采集数据格式

表1中，车型包括电动公交车、电动运输车、电动私家车、电动租赁车四大类;数据采集时间包括采集起始时间(Time_start)与采集结束时间(Time_end)。车辆SOC包括车辆起始SOC(Soc_start)与车辆结束SOC(Soc_end)；里程数默认为车辆里程计数器计数，包括起始里程数(Mileage_start)与结束里程数(Mileage_end)；行驶速度包括最大速度(Speed_max)与最小速度(Speed_min)。

1.2 数据预处理流程

采集到数据中存在一定数量的异常数据与数据缺失情况(见图1)，按Step1～Step4对其进行预处理，删除异常数据并补充缺失部分。

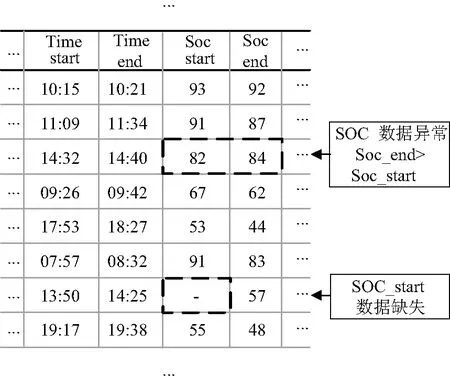
图1 异常数据与数据缺失

Step 1：输入数据，根据电动汽车公司统计数据得知，车辆启动到车辆停止至少需要4 min，各车型单次用车时间小于12 h，即满足条件4 min≤ (Time_end-Time_start)≤12 h，否则将其删除；

Step 2：由于采集的数据为用车信息，不包含电动汽车充电数据，若满足Soc_end>Soc_start且Soc_start≤100，否则将其删除；

Step 3：默认里程计数满足条件Mileage_end> Mlieage_start，根据用户用车经验值，单次行驶里程同时满足(Mileage_end- Mlieage_start)≤100 km，否则将其删除；

Step 4：假设采集到的数据为某一完整的行驶过程，则该过程中最小速度满足条件Speed_min=0，否则将其删除。

由于数据采集过程中会收到通信质量、收发端不稳定等因素影响，会有部分数据缺失关键信息或丢失等现象，针对此情况，本研究过程采用拉格朗日插值法[18]进行补充，。经过预处理后，异常数据占比最大不超过2%(见表2)。

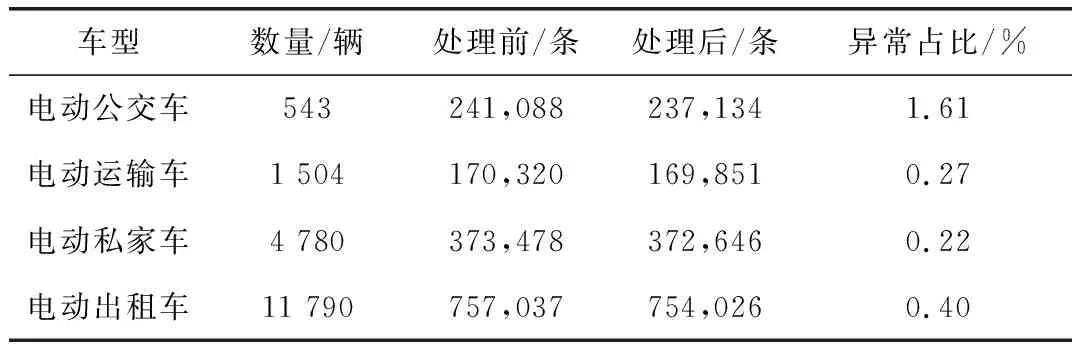
表2 各车型采集数据预处理结果

2 多类型电动汽车用车行为分析

基于数据预处理结果，采用数学统计方法对15 419 223条订单数据进行聚类分析，从用户出行里程、用户停车率量方面进行线性回归分析，分别按24 h(每日)的时间跨度进行用户出行规律归纳，并建立了相关用车行为模型(见图2)。

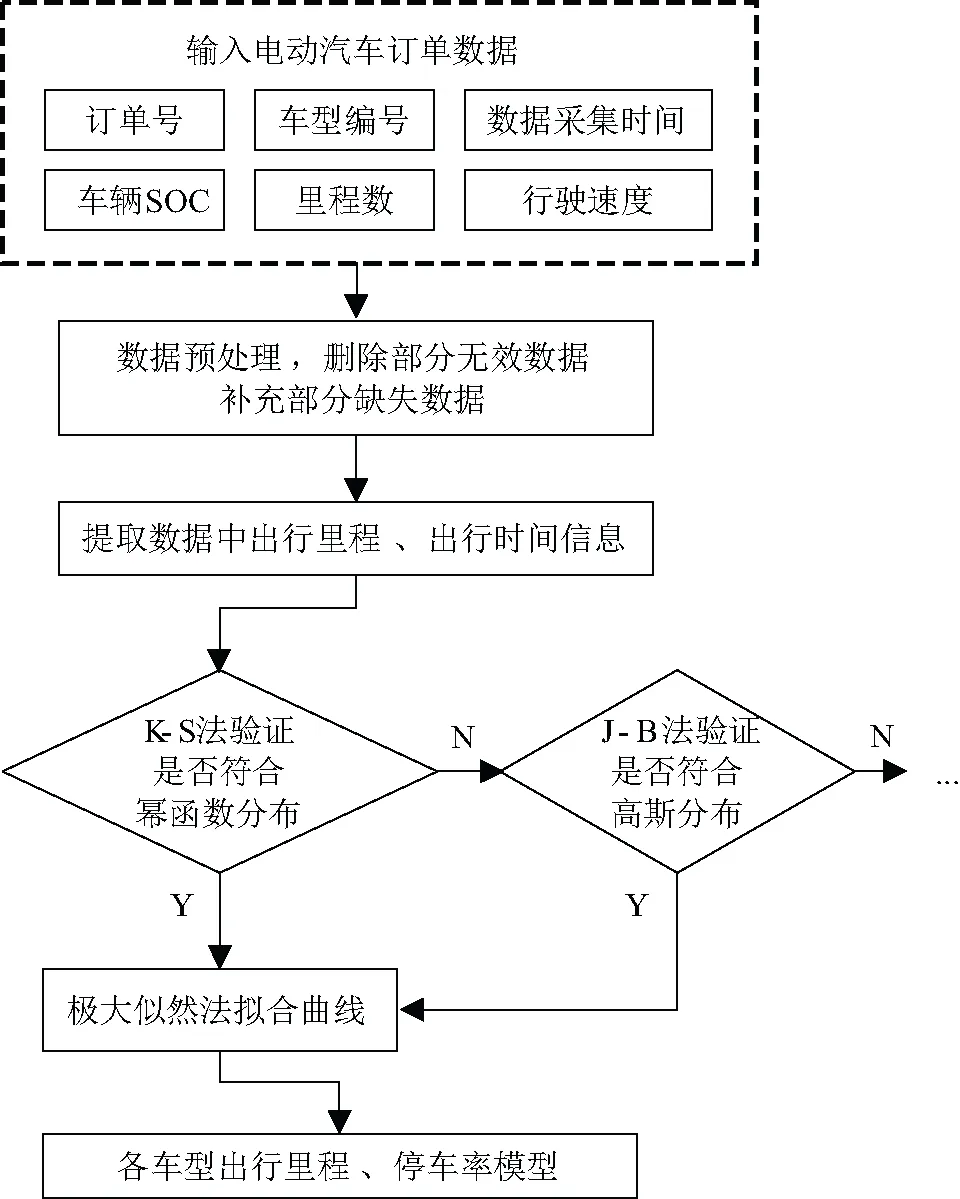
图2 多类型电动汽车用车行为分析流程

如图2所示，首先逐条输入采集到的的电动汽车订单数据，格式如表1所示；然后按1.2章节对数据进行预处理，删除部分无效数据并对部分缺失数据进行补充；提取数据中的出行里程与出行时间信息，分别采用K-S(Kolmogorov-Smirnov)法、J-B(Jarque-Bera)法等方法验证分布特性，并采用极大似然法拟合曲线，最后形成出行里程、停车率模型。

2.1 各车型用户出行里程分布

将订单数据按用户单次出行距离进行分类，即单次出行距离=(Mileage_end-Mileage_start)，分组间隔为5 km，得到所示的用户出行里程分布(见图3)。

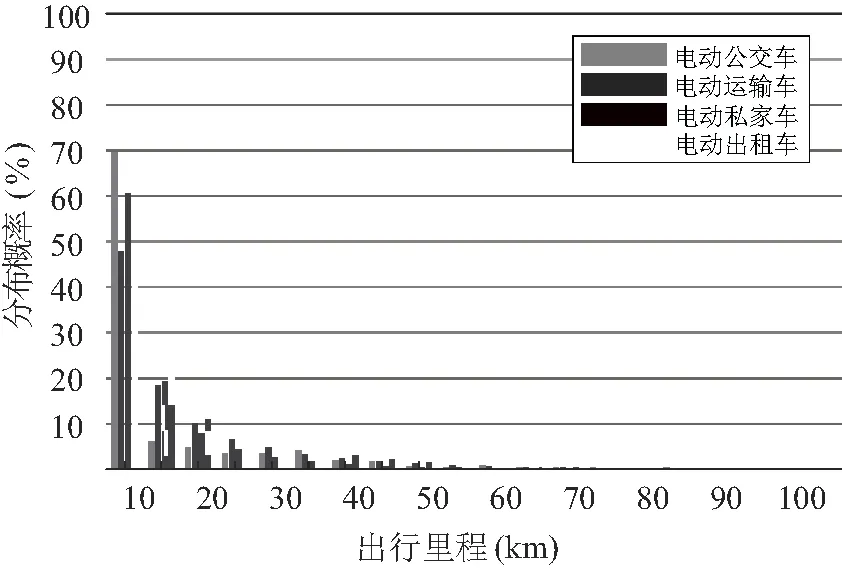
图3 用户出行里程分布图

分别对各车型用户数据采用K-S检验(Kolmogorov-Smirnov检验)方法进行检验，即：

(1)

(2)

(3)

式中Fn(x)为样本集的累计分布函数；F(x)为假设的理论分布函数；I为幂函数。基于Glivenko-Cantelli理论，若Xi服从理论分布F(x)，则n趋于无穷时Dn趋于0。本节假设用户用车里程服从幂函数分布，采用K-S方法检验，然后由极大似然法拟合曲线，得到分布模型(见表3)。

表3 多车型用户出行里程分布模型

2.2 各车型用户停车时间分布

数据经过预处理后，对每日的分时用车数量进行统计分析，间隔取1 h，可得每日0～24 h的用车数量分布(见图4)。

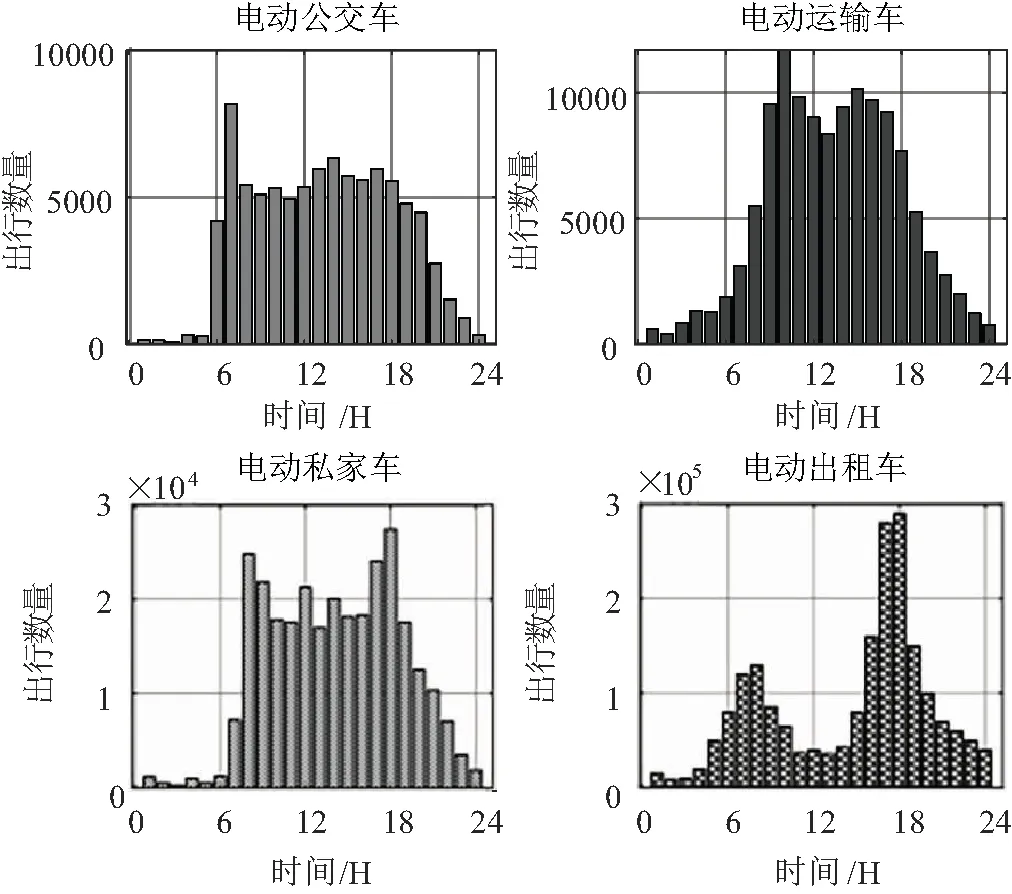
图4 多车型每日分时出行数量分布

将图4所示数据按式(4)进行处理，进一步得到各车型用户的分时停车率信息。

(4)

式中SCk(i)为i时刻第k种车型的停车率；CAk(i)为i时刻第k种车型的出行数量；CAk为统计数据中第k种车型的总数量，将图4所示的出行数量转化为用户停车率分布,如图5所示。

图5 多车型每日分时停车率分布

3 多类型电动汽车充电负荷建模

根据第2章的统计结果，已知电动汽车单日出行里程服从表3所示的分布函数。结合充电时间、电池参数等对电动汽车充电负荷进行模拟仿真。

3.1 电池参数设置

假设电动汽车为已知电动汽车车型、常规行驶电池耗量、以及充电桩功率，充电需求时间为：

(5)

式中e为该车型每公里耗电量(kWh/km)；Xcar为该车型每日的出行里程数(km)；Pcharge为该充电桩的充电功率(快充与慢充)；T为充电需求时间。参考市场上的具体车型数据，四类电动汽车车型具体参数如表4所示。

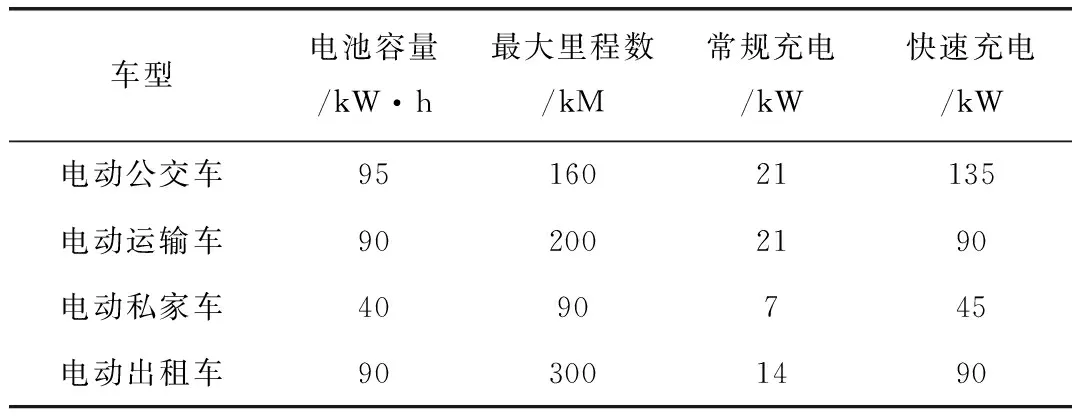
表4 四类电动汽车参数

3.2 充电时间概率分布

若当第i条数据的Soc_end小于第i+1条数据的Soc_start，则可认为第i条数据的Time_end为充电起始时刻。结合2.2节统计结果与车辆运行规律，对每日充电次数、充电类型选择、分布概率模型加以数学约束，则可估计多车型的充电时间概率分布(见表5)。

表5 多车型充电时间分布

电动私家车具有的非盈利特性，默认其充电不设限制时长，即每次充电直至充满电为止。

3.3 电动汽车充电负荷仿真

将表5的充电时间分布结合蒙特卡洛模拟法(Monte Carlo)，即可对区域集群性的电动汽车负荷进行模拟仿真，通过产生随机数来模拟具有不确定性的电动汽车充电行为(见图6)。

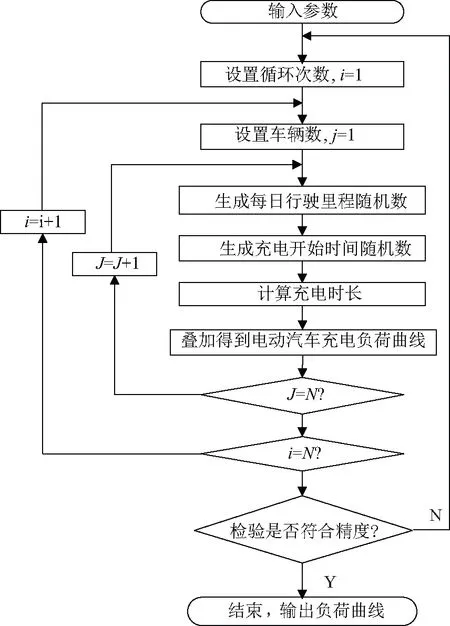
图6 电动汽车负荷仿真流程

为了简化计算流程，仿真设定了下列条件：

(1)由于在大部分电池的充电过程中，恒流充电占据了主导地位[19]，所有类型充电方式视为恒流充电，且忽略其他随机因素的影响；

(2)所有车辆只在表5所示的规定时段内充电，其他时段充电负荷量予以忽略；

(3)区域内的总负荷为独立车辆充电负荷的叠加，即对同时刻的不同车型充电负荷进行求和。

根据2030年中国汽车保有量按等比例设置电动公交车500 辆，电动运输车800 辆，电动私家车20 000 辆，电动出租车1 000 辆，不考虑私家车的工作日/休息日用车行为差异[20-21]。仿真结果精确至分钟，循环次数N=5 000。按图6的流程，抽取每日行驶里程与充电开始时间，并计算充电时长，形成各车型充电曲线(见图7)。

图7 各车型充电负荷仿真结果

为量化评价各车型的充电负荷，统计各车型充电量占比以及峰值最大负荷(见表6)。

根据图8与表6，由于电动私家车的数量较多，电动出租车默认采用快速充电模式，二者产生的负荷峰值远高于电动公交车与电动运输车，同时电动私家车、电动出租车为充电负荷的主要来源，分别占比54.51%与23.80%。将图8的各车型充电负荷累加，可得该区域内的电动汽车集群充电负荷。

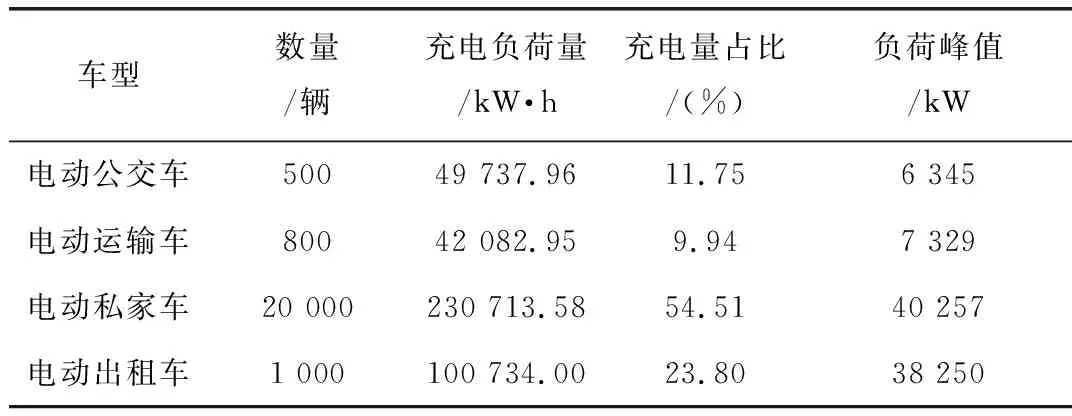
表6 各车型充电负荷占比

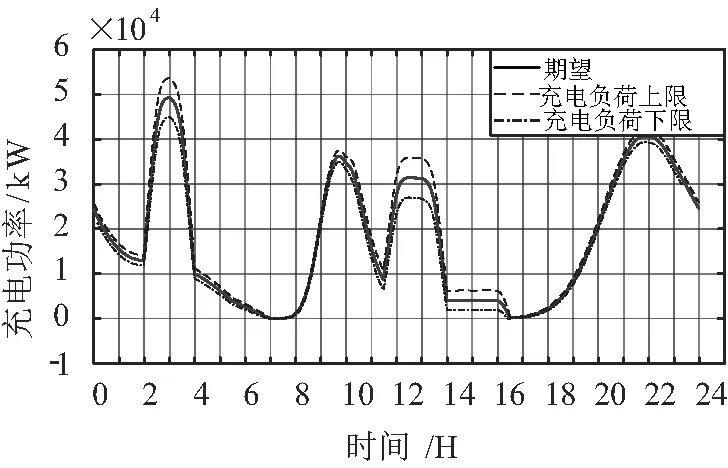
图8 电动汽车负荷仿真结果

为量化电动汽车集群对区域用电负荷的影响，结合某地区的典型日用电负荷(精确至分钟)，分析电动汽车负荷对电网的影响(见图9)。

图9 电动汽车负荷对电网的影响

图9中，由于四种类型的电动汽车均处于无序充电状态，9:00～15:00之间出现了“峰上加峰”现象，电网运行负荷进一步增加。同时，由于电动汽车的移动储能特性，23:00～05:00之间的谷时负荷得到了一定的补充。

4 结束语

基于电动汽车平台的实测数据，对数据进行了分析与处理，删除部分异常数据；通过分析电动汽车用户的用车里程与停车时间分布，得到不同用户的用车行为模型；通过蒙特卡洛模拟法对四种类型电动汽车的总充电负荷进行了仿真分析，得出以下结论：

(1)电动私家车、电动出租车的充电量占比较大，具有巨大的电网调度空间，结合具体运营模式，有潜力作为新能源并网的缓冲储能设施以及负荷侧削峰填谷的重要手段；

(2)针对具体区域的电动汽车负荷，在无序充电的情况下会产生不同程度的“峰上加峰”的情况，增加电网峰谷差，降低运行效率。可以结合分时电价、有序充电等策略引导负荷转移，减少电网运行压力与用户充电成本。