基于改进LSTM的电力设备状态融合预测模型

崔昊杨，周坤，胡丰晔，张宇，夏晟

(上海电力大学， 上海 200090)

0 引 言

掌握电力设备状态渐变规律，并从大数据的角度预估其后续趋势，是泛在电力物联网变电设备状态智能感知建设的内在要求[1]。虽然规模剧增的电力设备和日益丰富的检测手段，为设备状态内在趋势的挖掘和预测提供了丰富的数据基础[1-2]，但是传统的数据挖据方式需要建立复杂的数学、物理模型，在设备结构复杂性和运行状态不确定性高的背景下，海量数据分析面临低效化、片面化等问题。此外，部分老旧设备由于缺乏精细化管理，数据缺失、不规范的状况较多[3]。因此，全面且客观的从海量、残缺的历史检测数据中挖掘出有价值的状态变化规律、预判状态趋势发展，是电力大数据发展的核心问题。

目前，统计分析模型和机器学习模型利用多源异构检测数据从数据的角度揭示设备状态的变化规律，并且结合气象环境、运行环境等因素可对后续运行趋势进行个性化预估，已被广泛用于大数据背景下的设备状态评估及预测[4-5]。然而，以ARIMA为代表的统计分析模型虽然具有不需人为干预、架构简单、准确率高的优点[6]，但是只能处理线性关系显著、规律性和周期性较强的平稳数据。以LSTM为代表的机器学习模型虽然克服了传统机器学习因梯度消失而不能长期预测和预测准确率低的问题[7]，但对数据的时序性和完整性有着极高要求，运维人员的漏检、不定期检测使得检测数据不能严格按照固定的间隔分布在时间序列上，这些断层式的波动数据会损坏其“记忆细胞”，从而降低了泛化能力，导致内在规律预测的准确性难以保证。

针对目前电力大数据存在的问题以及上述两种常用模型的优缺点，提出一种基于改进LSTM的电力设备状态融合预测模型。该模型将数据映射到时间轴上进行平稳性分析和缺值检测，采用ARIAM模型根据缺失前的历史数据段进行缺值预测，并将预测得到的数值补充到原始数据中的对应空缺位置，从而得到平稳、完整的“新数据”；将“新数据”输入到改进LSTM模型和ARIMA模型中进行长期趋势和周期趋势预测；根据改进LSTM学习的准确率和ARIAM拟合趋势的吻合度分别对两个模型的预测值进行权重分配，通过加权融合方法对预测数据进行修正，达到状态趋势融合预测的目的。实验结果表明，提出的预测模型在负荷数据完整和缺失的情况下的预测准确率均高于ARIMA和LSTM单一模型。

1 电力大数据特性分析

电力设备的状态检测数据贯穿其建设、运行全寿命周期，然而，较早的设备状态检测数据只能靠人工记录，数据随机、漏检等情况时常导致状态数据的时序性、完整性较差，降低了状态趋势预测的准确度[8]。因此，重点研究了如何改善数据质量和提高预测准确率。实验的数据来源于2018年国内某市区历史负荷，采样周期为1 h，具备电力大数据的数量庞大、数据高速和数据价值等特性[9-11]，而且所采用数据通过计算机记录的方式使得数据具有较高的完整性。这里需说明，数据缺失的预测实验则通过人为方式随机的剔除部分数据，以验证文中模型相对于传统预测模型在数据残缺情况下的优越性。此外，本次用于训练和验证的负荷数据均为冬季的电负荷，不同月份的环境温度、节假日等因素对负荷的影响可视为等同的(春节除外)。

LSTM模型与ARIMA模型在负荷数据完整情况下和负荷数据残缺情况下的预测图及局部放大图如图1所示，其中的样本数据由训练数据P和测试数据p组成。为了便于比较，采用均方根误差(Root Mean Square Error , RMSE)作为预测准确性的评估依据，计算公式为：

(1)

式中p为测试数据真实值；p′a为预测值。从图1(a)中可知，数据完整情况下的LSTM模型预测的RMSE为392，误差率比RMSE为450的ARIMA模型低了13%。从图1(b)可知，ARIAM模型在历史数据残缺情况下的预测RMSE为699，增幅达到了57%，设备状态趋势的真实性难以保证，而LSTM甚至无法完成训练和预测功能。此外，从图1(b)还可知，残缺数据导致了ARIMA预测的趋势呈现出无序的周期性波动，这是由于ARIMA模型将每个割裂的数据段视为一个或多个完整周期内的数据，丧失了周期性趋势随长期趋势发展的变化规律。由此可见，完整、平稳的状态数据是保证趋势预测准确率的前提。

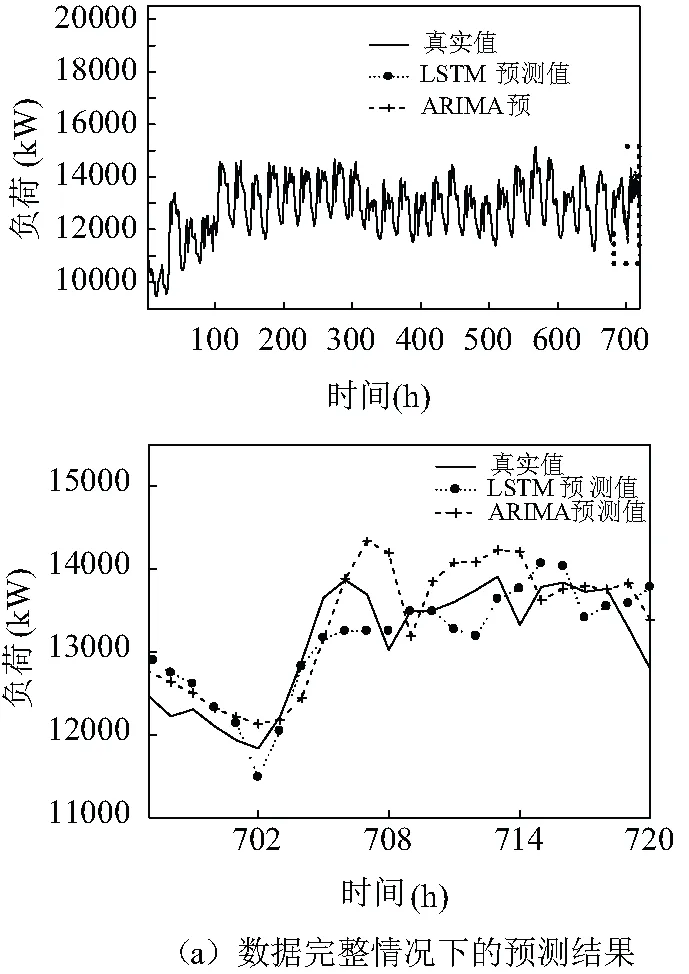
图1 LSTM、ARIAM模型在数据完整和数据残缺情况下的预测结果

2 基于改进LSTM的电力设备状态融合预测模型

针对数据残缺对趋势预测的影响，以及ARIAM模型和LSTM模型各自优势，文中提出了基于改进LSTM的电力设备状态融合预测模型。该模型主要包含基于ARIAM自适应分段预测的数据完整性提升、改进LSTM模型预测以及融合预测3个环节。

2.1 基于ARIAM自适应分段预测的数据完整性提升

预测前先对数据序列{D(t)}的平稳性进行检测，以数据缺失的位置作为分界点将数据分为s+1个数据段Ds，并记录数据缺失位置s，s=1,2…。将数据段D1输入到G(t)ARIMA模型中，用以预测第一个缺失数据d1。把得到的d1补全到D1和D2的缺失位置，得到的新数据段再次输入到G(t)ARIMA模型中，用以预测第二个缺失数据d2，以此类推直到将数据补齐，得到“新数据”序列{D′(t)}，即：

(2)

ds=GARIMA(D1+d1+…+Ds-1)

(3)

GARIMA(t)=θ0+φ1G(t-1)ARIMA+…+

φjG(t-j)ARIMA+εt-θ1εt-1-…-θjεt-j

(4)

式中φj(j=1, 2, …,s)和θj(j=1,2,…,s)为模型参数；εt为独立正太分布的白噪声。

2.2 改进LSTM模型预测

LSTM模型不仅有传统RNN不具备的输入门it、输出门ot和忘记门ft，还多了一条可长期记忆的信息流ct，在大数据预测的领域具有举足轻重的地位[12]。当“新数据”{D′(t)}输入到G(t)LSTM模型时，遗忘门会将其映射到[0,1]区间，然后与长期记忆的信息相乘对记忆中的数据进行筛选和更新，在经过输入门得到记忆的更新数据，最后通过输出门得到预测数值ht[13]，即：

(5)

G(t)LSTM=it=σ·wi·[ht-1,{D′(t)}]+σ·bi

(6)

但是，ARIMA预测得到的“新数据”{D′(t)}存在着部分数据失真的问题。为此，文中通过对遗忘门ft加权的方式对LSTM模型进行改进。计算缺失数据ds附近的原始数据段D(s)与ARIMA拟合数据段yARIMA(s)的平均绝对误差μs，以及原始数据段D(s+1) 与ARIMA预测得到的新数据段D′(s+1)的平均绝对误差μs+1,如图2所示。

图2 改进遗忘门后的LSTM预测模型

在获取上述平均绝对误差的基础上对遗忘门进行赋权，从逻辑上达到自适应去除误差保留全程长期记忆趋势的目的，此时的式(5)修改为：

(7)

(8)

2.3 状态趋势融合预测

为了增强文中模型的容错能力，缩小预测值与真实值之间的置信区间，从而提高状态预测的准确率，文中通过加权融合[14-15]的方法将ARIAM预测的周期趋势和改进LSTM预测的长期趋势进行融合，以此来降低预测误差。首先，建立“新数据”序列{D′(t)}在G(t)ARIMA模型的学习绝对误差函数矩阵E(t)和在G(t)改进LSTM模型中的拟合绝对误差函数矩阵E′(t)，即：

(9)

(10)

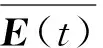
1=qk+q′k,k=1,2,…,T

(11)

(12)

(13)

(14)

(15)

将ARIMA和改进LSTM根据新序列{D′(t)}得到的预测数据p=[p1，p2,…,pm]、p’=[p′1，p′2,…,p′m]与周期内相对应的权重相乘[16]，得到最后趋势数据序列{y(t)}为：

{y(t)}=[y1,y2,…,ym]=p′×q′+p×q=[p1·q1+p′1·q′1,p2·q2+p′2·q′2,…,pT·qT+p′T·q′T,

pT+1·qT+1+p′T+1·q′T+1,…]

(16)

3 实验分析

为了验证文中模型在数据完整或数据残缺的情况下均具有较高的准确率和可靠性，进行了以下实验。实验分析分为两部分，第1部分为“数据质量对比”，选用绝对百分比误差作为补齐后数据和完整数据之间的失真对比指标；第2部分为“预测准确性对比”，采用RMSE作为文中模型、LSTM、ARIMA的性能对比指标。

3.1 数据质量改善对比

通过ARIAM对残缺的负荷数据进行预测，逐步弥补缺失数据，采用绝对百分比误差r(%)对修补数据的真实性进行评判：

(17)

式中PARIMA为ARIAM模型预测得到的用于填补缺失的数据，P为训练数据真实值。补齐后的数据及其误差如图3所示，与真实值的绝对误差均在15%以下，说明了ARIMA模型能较为准确地还原出数据规律，降低数据失真的可能性。并且补齐后的序列将数据之间的关系“串联”起来，有效地避免了“断层”数据对后续趋势预测的影响。由于初期数据较少，导致了前5个补充值的预测误差较大，但是随着数据逐渐增多，数据周期趋势和长期趋势更加清晰，有效抑制了后续预测误差。

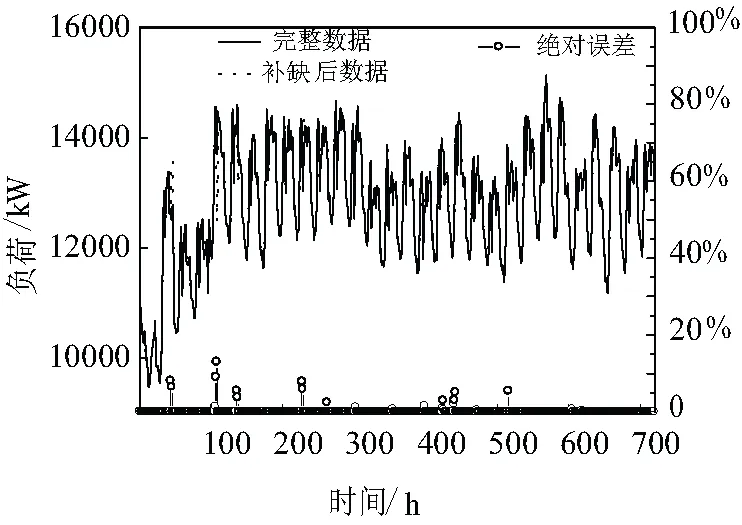
图3 “新数据”与原完整数据真实性对比

3.2 预测准确性对比

数据完整情况下ARIAM、LSTM和文中模型的预测结果和局部放大结果如图4所示，文中模型的预测结果RMSE为295，准确率相比于ARIAM和LSTM分别提高了52%、25%。这说明文中根据改进LSTM学习情况和ARIAM拟合情况，对一个周期里不同时刻预测值分配权重的方法能达到“取长补短”的效果，降低了误差较大数据的影响。

图4 数据完整情况下文中模型、ARIAM和LSTM预测对比

从图5和表1中可知，在数据残缺的情况下，经过文中模型处理后的“新数据”的平稳性得到了显著提升，并且数据的长期趋势和周期趋势会随着“串联”数据的增多而愈发显著，此时的LSTM完成了训练和预测任务预测的RMSE为862，而ARIMA预测的RMSE相比于数据缺失情况下降低了6%，为658。而文中模型利用“新数据”预测的RMSE为371，相对于同等情况下ARIAM预测和LSTM预测的准确率则分别高出了44%和57%，比数据缺失时的ARIAM预测提高了46%。以上对比数据说明，由于文中模型具备了ARIAM的周期预测趋势和LSTM的长期预测趋势，较好地呈现了周期趋势围绕长期趋势变化的规律，并且改进遗忘门后的LSTM降低了“新数据”失真所带来干扰。

另一方面，文中模型、ARIAM和LSTM利用“新数据”预测的准确率比数据完整情况下的准确率分别降低了26%、46%和120%，这是由于初期数据较少而导致ARIAM补缺时的误差较大，这样的误差在传统LSTM训练过程中被逐次放大，并且随着补缺数据的增多，误差也会逐渐增大，进而降低了预测准确率。然而，文中模型对LSTM遗忘门进行的改进有效降低了数据失真所带来的影响，抑制误差的能力会随着数据的增加而增强。因此，文中模型不仅通过改进LSTM遗忘门的方式有效缩小了预测值与真实值之间的置信区间，还采取融合预测的方法从全景的角度对数据进行分析，满足大数据背景下的设备状态全景掌控和状态趋势的精准预估。

图5 “新数据”情况下文中模型、ARIAM和LSTM预测对比

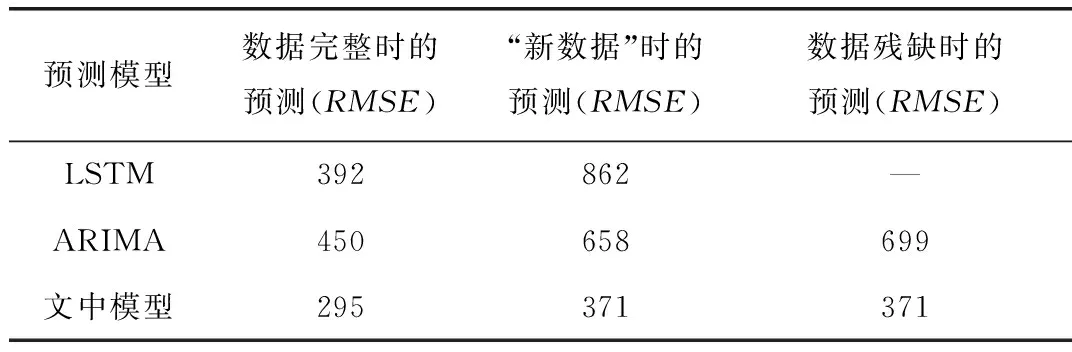
表1 数据完整、残缺和“新数据”情况下的文中模型、ARIAM和LSTM的RMSE对比

4 结束语

文中针对现有的电力大数据所存在完整性、规范性较差问题，以及传统LSTM模型与ARIMA模型各自的特点，开展了如下研究：

(1)使用ARIMA预测模型根据历史数据进行“查缺补漏”的方式解决了大数据的不规范、残缺问题，得到了有利于趋势预测的平稳、完整数据；

(2)对LSTM的遗忘门进行改进，有效地降低了误差数据对记忆细胞的影响，较好地呈现了数据的长期趋势；

(3)利用加权融合的方法对ARIMA和改进LSTM预测值进行修正，充分利用了全局趋势和周期趋势，能够更为准确地预测数据变化趋势。实验结果表明，不论是数据完整还是数据残缺的情况，文中模型相较于LSTM和ARIMA的预测精度都大幅提高。