基于WD-LSSVM-LSTM模型的短期电力负荷预测

赵倩，郑贵林

(武汉大学 电气与自动化学院， 武汉 430072)

0 引 言

随着经济社会的发展，电力需求呈现出不断飙升与峰谷差愈来愈显著的态势，因此，需求侧负荷预测成为电力系统源-网-荷协调调度的一项重要技术。准确的需求侧负荷预测，对于电力供需平衡、电力系统稳定、保障电力服务、有效地降低发电成本等有着重大意义。

许多学者对需求侧负荷预测开展了多方位的研究，提出了多种预测方法，如线性外推法、回归分析法、时间序列法、小波分析法、人工神经网络法、支持向量机法以及组合预测法等[1-8]。

由于电力需求侧的特点，千家万户、千变万化、千姿百态，具有随机变化性强，非线性显著，近年来，对于需求侧负荷预测的研究工作也倾向于先对负荷进行分解之后再进行预测，也产生了很多负荷分解方法，如小波分解法[9]、改进局域均值分解法[10]、频域分解法[11]等。

由于单一的预测方法都有其局限性，因此组合预测的方法应运而生。第一类方法是进行多组单一方法预测，将预测结果通过权重分配进行组合得到预测结果。但是，基于权重的组合预测算法中模型的拓展性较差。第二类方法即为负荷分解的方法，最常用的是小波变化和EMD分解。

小波分解适用于分解非平稳信号且分解速度较快，文中将电力负荷数据通过小波分解的方法分解为频率不同的若干分量，对较为平稳的低频分量建立PSO-LSSVM预测模型进行预测，对变化较大的高频分量通过LSTM网络进行预测，将所得结果叠加还原，得到最后的预测结果。

1 基本原理

1.1 小波变换

小波变换是在克服傅里叶变换缺点的基础上发展而来的一种新的变换方法。它是一种在时间和频域的局域变换，主要通过对信号的伸缩平移运算实现对信号的多尺度细化，它能够提供目标信号各个频率子段的频率信息，非常适用于非稳定信号的分析。

文中利用小波分解算法将用电量离散时间序列分解为不同频率的分量，但是分解后得到的分量长度不同，而且长度不同于原始数据，因此需要对这些分量进行小波重构[12]，进而得到和原始数据长度相等、频率不同的分量，如图1所示。

图1 小波分解与重构结果

图1中，s为原数据波形;a5为变化缓慢的低频分量，包含信号的低频信息；d1、d2、d3、d4、d5是变化迅速的高频分量，包含信号的高频信息。

1.2 支持向量机算法

对于训练集中的一个样(xi,yi)，其函数间隔为：

ri=yi(Wxi+b)

(1)

训练集的函数间隔等于所有样本点的函数间隔的最小值：

(2)

函数间隔只能表示分类预测的正确性，不能表示样本到分隔超平面的准确距离。

对于训练集中的一个样本(xi,yi),其几何间隔为：

(3)

训练集的几何间隔等于所有样本点的几何间隔的最小值：

(4)

几何间隔不但可以表示分类预测的正确性还能准确地表示样本到分隔超平面的距离。

SVM的优化问题转化为最大化训练样本的几何距离：

(5)

s.t.yi(Wxi+b)≥r,i=1,2,…m

(6)

函数间隔的取值不会影响最优问题的解，将训练样本的函数间隔取值为1，上述问题转化为：

(7)

s.t.yi(Wxi+b)≥1,i=1,2,…m

(8)

由此可知SVM的优化问题是一个带有分等式约束的QP(Quandratic Programming)问题。

1.3 最小二乘支持向量机

LSSVM将SVM优化问题的非等式约束用等式约约束替换，具体形式如下：

(9)

s.t.yi(Wxi+b)=1,i=1,2,…m

(10)

为了解决存在部分特异点的情况，给每一个样本引入误差变量ei，并在原始函数中加入误差变量的L2正则项，这样LSSVM的优化问题就转化为：

(11)

s.t.yi(Wxi+b)=1-ei,i=1,2,…m

(12)

式中C为正则化参数，对于非线性可分的训练样本，可以将原始样本从映射到更高的线性可分的空间中，φ(xi)将xi映射到更高维空间中。LSSVM的优化问题是一个带有等式的约束的QP问题，为求解该问题，先列出上述优化问题的Lagrange函数：

(13)

式中αi表示对应于xi的lagrange乘子。lagrange函数对各个变量进行求道，并使导数为零：

(14)

(15)

(16)

(17)

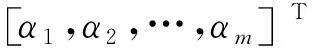
(18)

(19)

1.4 粒子群优化算法

粒子群优化算法(PSO)是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。

PSO初始化为一群随机粒子，然后通过迭代找到最优解，每次迭代粒子通过跟踪两个“极值”来更新自己，即个体最优解和种群最优解。所有的粒子通过一个适应度函数确定本身的适应值，用以判断目前位置的好坏。每个粒子仅具备速度和位置属性。

PSO的标准形式如式(20)、式(21)所示：

vi=ω×vi+c1×rand()×(pbestt-xi)+c2×rand()×(gbesti-xi),i=1,2,3…N

(20)

xi=xi+vi

(21)

(22)

式中ω为惯性权重；vi为粒子的速度；N为种群粒子数；rand()为介于(0,1)之间的随机数；xi为粒子的当前位置；c1和c2为学习因子；pbesti表示粒子经过的最好位置；gbesti表示种群所经历的最好位置。粒子通过pbestt和gbesti两个极值来更新自己。文章采用典型线性递减策略来确定惯性权重，如式(22)所示，ωmax为惯性权重最大值，ωmin为惯性权重最小值，t为当前迭代次数，tmax为总的迭代次数。

1.5 LSTM基本理论

LSTM网络是一种具有记忆的神经网络模型，使得处理时序的属性数据具有很好的效果。标准LSTM网络架构中的核心单元。主要通过通入门、遗忘门以及输出门这三个门达到了对网络具有记忆效果。基本的LSTM网络结构如图2所示。

图2 LSTM结构示意图

遗忘门决定从状态中丢弃什么信息，主要通过sigmoid函数去参考上一次的结果与当前的内容，其数学模型为：

ft=σ(Wf[ht-1,xt]+bf)

(23)

式中h为上一次输出的结果；x为当前输入的信息；ft为输出0到1的概率；Wf和bf为遗忘门权重矩阵和偏置项；σ表示sigmoid函数。

输入门作用是控制哪些信息被放入细胞状态值中，其数学模型如式(24)和式(25)所示：

it=σ(Wi[ht-1,xt]+bi)

(24)

(25)

(26)

式中ft表示遗忘门。

输出门确定细胞状态的哪个部分将输出，其数学模型为：

σt=σ(Wo[ht-1,xt]+bo)

(27)

ht=ot*tanh (Ct)

(28)

式中ot为输出门的输出；tanh为激活函数。

2 负荷预测方法研究

2.1 模型构建

该模型的主要思想是将用电量时间序列进行小波分解之后得到不同频率的分量，对各分量进行小波重构，然后对低频分量构建LSSVM预测模型，通过PSO算法找到LSSVM模型的最佳参数，对高频分量构建LSTM模型进行预测，将预测结果叠加在一起得到最终的预测结果。

2.2 LSSVM模型构建

如图3所示，在LSSVM建模过程中，重要的一个步骤是确定两个参数C和σ。只有设置合适的参数才能使模型得到较好的预测效果。

图3 WD-LSSVM-LSTM预测模型流程图

LSSVM建模的步骤如下：

步骤一：确定输入，对输入进行预处理并进行标准化；

步骤二：形成训练样本；

步骤三：确定参数C和σ；

步骤四：计算α、b参数，建立LSSVM预测模型；

步骤五：进行短期负荷预测。

2.3 PSO优化的LSSVM模型

为了使预测效果达到最大化，通过粒子群算法对LSSVM方法的核函数参数进行优化，建立PSO-LSSVM模型。

粒子群优化算法寻找最小二乘支持向量机最优参数的步骤如下：

步骤1：设定参数。设置粒子群优化算法的搜索范围：C∈[0.1,100],σ∈[0.1,10]；粒子数m=20；加速常数c1=c2=2；

步骤2:在速度区间和搜索空间上随机初始化粒子速度和位置；

步骤3:定义适应度函数。将pbesti和gbesti作为支持向量机的C和σ参数代入LSSVM模型，通过式(30)计算出每个粒子的适应值,式中fi为第i个粒子的适应值，n为样本个数，yij为第i个粒子的第j个样本的模型预测值，Yj为第j个样本的模型期望值。适应值最小的粒子的值记为前群体的最优位置。

(29)

步骤4:按照式(20)、式(21)更新粒子速度和位置。重复步骤3，计算更新后的每个粒子的适应值。最小值对应的粒子的两个极值作为LSSVM的最优参数；

步骤5:达到迭代次数后就结束搜索计算过程；

步骤6:将最优解作为LSSVM的参数，代入模型后进行负荷预测。

2.4 WD-LSTM预测模型

针对随机性较强的负荷分量，LSTM神经网络既有较强的非线性拟合能力，并且能够挖掘时间序列自身特征，使得预测结果尽可能准确。因此通过LSTM神经网络来预测负荷的高频分量。

WD-LSTM建模过程如下：

(1)采用WD分解技术将输入负荷分解成频率不同的分量；

(2)对分解后得到的负荷分量数据进行预处理，对数据进行归一化处理；

(3)实现LSTM模型，需要设置网络的相关参数。

文中选择当前时刻的前96个电力负荷数据作为网络的输入预测下一时刻的负荷数据，因此设置输入层节点数为96，输出层节点数为1。隐藏层采用LSTM细胞和Dropout搭建双层循环神经网络[13]。由于LSTM神经网络模块的层数越多，学习能力越强，但是层数过多又会造成网络训练难以收敛，因此训练过程中网络的层数一般不超过3层[14-15]，文中采用2层。文中隐藏层的每个LSTM层后面加入了一个Dropout层，在前向传播时让神经元的激活值以指定的概率停止工作，从而增强模型的泛化性，防止过拟合；

(4)对每个高频分量分别建立LSTM模型；

(5)在进行预测后，对预测值进行反归一化处理，然后将低频分量预测值和高频分量预测值进行叠加，得到最后的预测结果。

3 算例分析

3.1 试验数据和试验平台

试验以2016年电工数学建模竞赛[16]提供的2009年1月1日～2015年1月10日的电力负荷为数据，数据的采样周期为15分钟，每天产生96组数据。以2009年1月1日～2015年1月1日的数据为训练数据，以2015年1月2日～2015年1月9日的负荷数据为测试数据。预测1月10日的短期电力负荷，并与真实负荷进行对比。

3.2 电力负荷数据分析

选取连续三天的电力负荷数据做出变化曲线如图4所示。

图4 电力负荷变化曲线图

可以看出电力负荷数据有相似的波动规律，总体上与时间存在一定的周期关系。

3.3 数据预处理

对样本数据进行归一化处理，将其转化为无量纲的纯数值。这样不仅可以提升模型的收敛速度，还可以提升模型的精度。归一化公式如下所示：

(30)

式中Z′为归一化后的样本值；Z为原样本值；Zmax为原样本集中的最大值；Zmin为原样本集中的最小值。

3.4 实验仿真与结果

文中仿真实验使用matlab2016b编程软件进行分析。对归一化后的低频样本分量建立PSO-LSSVM预测模型进行预测，高频样本分量分别建立LSTM预测模型进行预存，得到各分量的初始预测值，之后对这些初始值进行反归一化得到实际预测值。最后，将各个样本分量的预测值进行叠加，得到最终的预测结果，做出预测值与实际值曲线的对比图，如图5所示。图5显示了基于小波分析的WD-LSSVM-LSTM预测模型的最终预测结果。

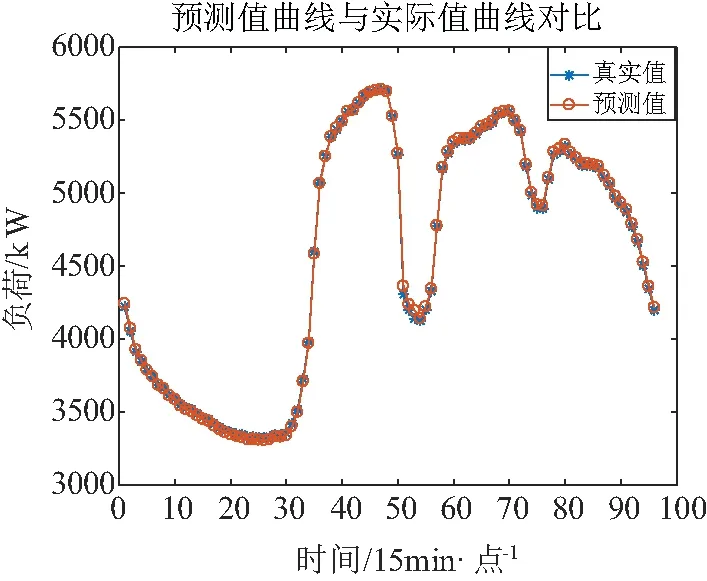
图5 基于小波分析的PSO-SVM模型预测结果

为了评估该模型的精确度，对负荷原始数据分别构建PSO-LSSVM预测模型、基于小波分析的PSO-LSSVM预测模型和BP神经网络预测模型进行预测，将所有预测模型的预测结果做出曲线对比图，如图6所示,并做出各模型的逐点相对误差如图7所示。

图6 几种预测模型预测结果

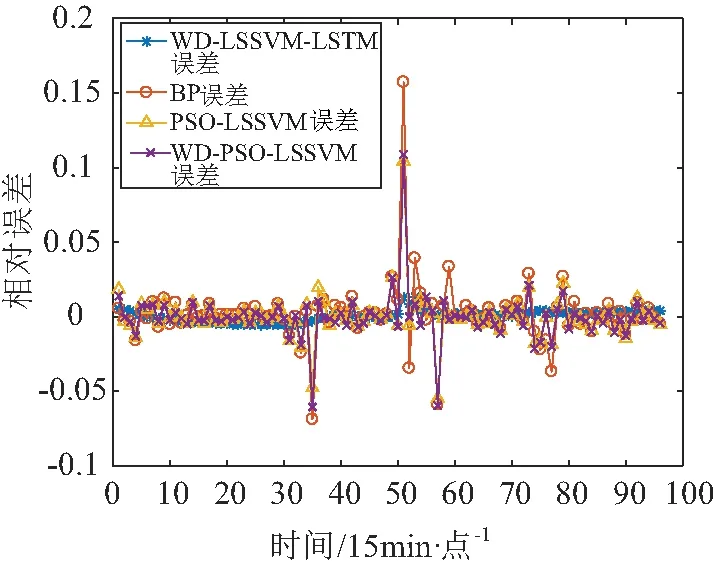
图7 逐点相对误差对比

为了比较这几种预测模型的精确性，选择平均绝对误差和均方根误差作为评价标准，有：

(31)

(32)

式中n为预测样本数量；xi为实际用电量；x′i为预测用电量。

经计算，得到几种预测模型预测结果的MAE值和RMSE值，如表1所示。

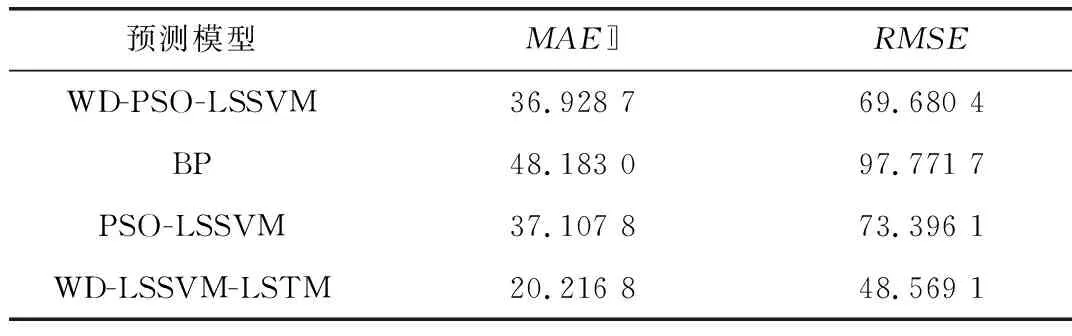
表1 几种预测模型预测结果的比较

可以看出WD-LSSVM-LSTM预测模型误差降低，精度有一定提升。

4 结束语

文中针对电力负荷预测提出了基于小波分析的LSSVM-LSTM预测模型。由于电力负荷随机变化性强，非线性显著，文章采用小波分析方法对电力负荷做了小波分解和重构，为优化的LSSVM模型和LSTM模型得到更高的预测精度提供了保障。对电力负荷进行WD分解，得到不同频率的分量，随后，分别采用PSO-LSSVM与LSTM网络对分解后的低频与高频负荷数据进行预测，将预测结果进行叠加，得到电力负荷预测结果。实验结果表明，该预测模型有较高的预测精度，整体上对电力负荷的趋势预测较为准确。文中研究的方法仍然需要进一步完善和改善，使预测的效果更加符合实际的需求。