静压转台油膜微倾斜参数下的热影响仿真研究

倪世钱， 张志全

(1. 南京交通职业技术学院 轨道交通学院，江苏 南京 211188；2. 哈尔滨理工大学 机械动力工程学院，黑龙江 哈尔滨 150080)

十九世纪初，科学家Navier和Stokes推算出研究黏性流体的一般性运动方程，确立了流体润滑支撑的理论基础，从此以后，流体动静压支撑的理论研究不断发展并在静压转台等领域得到广泛应用.Osman T A等[1]分别通过有限差分法和有限元法数值迭代求解了环形和扇形油腔推力轴承的油膜压力分布方程，得到了静态载荷下轴承的承载能力、流速和阻尼系统随着油膜厚度变化的曲线.孟曙光等[2]简化了深浅动静压混合轴承的油膜压力分布，利用数值解析算法模拟了轴承的承载能力和温升.马建刚等[3]为了提高热变形仿真的精度，通过优化发热量等计算方法以及合理设计分析流程，研究了同一转速下各热源处温升随时间的变化曲线.于晓东等[4]研究了不同工况下静压推力轴承对流换热不同，进一步导致工作台和底座热变形不均匀.张艳芹等[5]研究了从轴承摩擦副润滑机理出发，斜面式矩形油垫静压轴承油膜热油携带现象.刘志峰等[6]利用有限差分法建立了不同转速下油垫温度分布与重载静压转台承载性能的变化关系.

采用静压转台的数控装备多为重型装备，其转台结构尺寸较大，线速度高，特别是极端工况下转台润滑油膜的温升效应将直接影响到转台的加工精度，因此，准确预测出转台润滑油膜热场成为提高数控装备的关键难题.本文对微倾斜油垫静压转台油膜热场进行仿真研究，从理论上揭示出不同微倾斜参数下高速极端工况下的油膜温度分布规律，为静压转台润滑设计提供理论依据.

1 数学模型

1.1 32号液压油黏-温模型

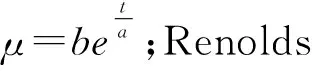
表1 32号液压油黏温数据

本研究选取以上8组数据来构造和拟合Vogel黏温方程，得到黏温方程表达式：

(1)

式中μ为动力黏度(Pa·S)，T为平均温度(℃).

1.2 油膜热计算控制方程

油膜运行中，依据能量守恒定律，能量方程基本表达方式为：

(2)

上式可写为：

(3)

其中：Cp为比热容(j/kg·K)；k为导热系数；T为温度(K)；ST为热源项,本研究中无外部热源项，即式中ST=0.

2 静压转台结构及油垫微倾斜参数

静压底座及油垫实物图如图1所示，由于油垫在导轨上呈周期性均匀分布，每个油垫间设有阶梯状的回油槽，因此在仿真计算时取整体油膜的1/12油垫进行计算分析，通过solidworks三维软件建立底座及油垫1/12几何模型如图2所示.

图1 静压底座与油垫实物图

图2 底座与微倾斜油垫1/12模型

在三维图中，对双矩形腔的周向进行剖析(图3).可以看出将液压油从输油管路从两个进油口流入到双矩形油腔内，随后从封油边流出双矩形腔，进入回油槽中.在整个过程中，会有一部分液压油从双矩形腔中溢出，流到两个矩形腔中间的凹槽中，最后流出到回油槽.原始的平行平板油膜高度为0.1 mm，油垫微倾斜后，最大倾斜高度为h2，最小倾斜高度为h1，则微倾斜参数用Δh=|h1-h2|表示，其中h1依次取值0.10 mm、0.09 mm、0.08 mm、0.07 mm、0.06 mm、0.05 mm，对应h2依次取值0.10 mm、0.11 mm、0.12 mm、0.13 mm、0.14 mm、0.15 mm.

图3 可倾式油垫周向剖面图

3 油膜微倾斜参数下热场计算

3.1 微倾斜参数对油膜发热的影响

通过计算不同楔形高度油膜热场探索出微倾斜参数对楔形油膜温度场的影响规律.本研究静压转台为顺时针旋转且转速为100 r/min，经计算油膜流态为层流，初始油膜厚度为0.01 mm，在此条件下，分别对0～30 t载荷范围内0 mm、0.02 mm、0.04 mm、0.06 mm、0.08 mm、0.10 mm时的油膜热场进行数值模拟，图4为负载20 t的油膜热场分布.由图4可以看出，油膜的热场温度值分布不均匀，局部有明显的高温区，且高温区主要集中在油垫径向封油边区域，最大值集中在径向外侧封油边处，并且随着倾斜值的变大，封油边处高温区集中的越发明显.分析原因为工作台旋转时存在库埃特流动现象，造成温度场不均匀；油膜受剪切流和压差流的影响，高温出现在径向外侧封油边处；另外，由于油膜楔形的影响，高温侧膜厚较小，使得高温油液在此处聚集，形成顺流侧径向外侧处的局部高温.

图4 油膜微倾斜参数下的热场分布

为显示油腔温度值变化情况，经后处理分析得出周向、径向对称面上温度值，如图5所示.可以看出随着油膜楔形高度的变大，油膜最高温度值有所增加，这是因为楔形长度不变的情况下，楔形高度越大，润滑油流进(出)油腔内的流速越慢，进入油腔的室温(流出油腔的高温)润滑油稍少一些，热油很难带走.其中顺流侧的平均温度低于逆流侧的平均温度，主要由于逆流侧封油边剪切流和压差流流向相反导致油腔内部的热油不能及时的疏散造成的.

图5 油膜的温度分布散点图

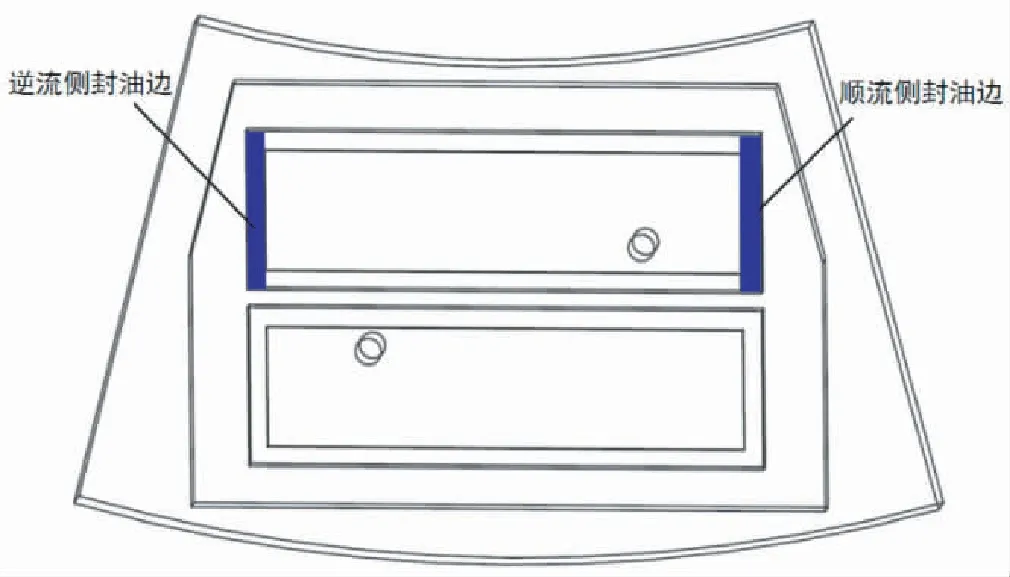
图6 封油边处温度分析区域

3.2 油膜热场计算结果分析

静压转台顺时针旋转时，如图6所示，油膜楔形参数值较小的一侧为顺流侧封油边，反之为逆流侧封油边，通过CFD-Post后处理模块创建顺、逆流侧封油边油膜温度监测区域，提取该区域数据，得到不同楔形参数所影响各区域的温度值，其中顺、逆流侧平均及最高温度的变化曲线如图7、图8所示.

图7 油膜微倾斜参数下顺流侧处温度随负载变化曲线

图8 油膜微倾斜参数下逆流侧处温度随负载变化曲线

从以上数据可以得出载荷20 t时，油膜微倾斜参数与封油边处平均和最高温度之间的关系曲线如图9所示.通过对油膜热场计算结果曲线分析可知，转速一定时，轴承油膜温升与载荷呈反比关系；低载荷工况，各倾斜参数下封油边处平均温度值相差不大，随着载荷的增加平均温度变化明显；而低载荷时油膜最高温度在各倾斜参数下差值较大，随着载荷的增加油膜最高温度值相差反而不大.整体可看出，油膜微倾斜参数对油膜平均温度值影响不大，但对油膜最高温度值影响很大，且顺流侧的最高温度值较逆流侧最高温度值大较多，且随着倾斜度增加其差值逐渐增大，分析原因主要是由于受微倾斜影响，静压转台运行形成的倾斜油膜有封压及憋流的现象，且顺流侧形成了最薄油膜区域，此处液流液阻增加导致流量减小，从而对润滑油形成的剪切热不能有效疏散导致顺流侧最高温度值较大.

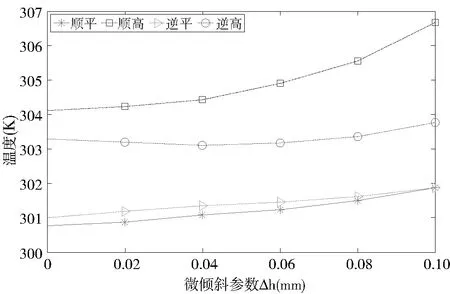
图9 油膜温度随微倾斜参数变化曲线

本研究得到不同微倾斜参数下的各工况油膜平均温升约5 K，最薄油膜处的油膜最高温升约14 K左右，从油膜温度值变化曲线及油膜热场综合分析可知，微倾斜参数下油膜润滑较适用于重载工况条件.

4 结论

(1) 通过对静压转台0～30 t载荷工况油膜热场计算，发现油膜的热场温度值分布不均匀，局部有明显的高温区，且高温区主要集中在油垫径向封油边区域，最大值集中在径向外侧封油边处，并且随着倾斜值的变大，封油边处高温区集中的越发明显.

(2) 转速一定时，轴承油膜温升与载荷呈反比关系；低载荷工况，各倾斜参数下封油边处平均温度值相差不大，随着载荷的增加平均温度变化明显；而低载荷时油膜最高温度在各倾斜参数下差值较大，随着载荷的增加油膜最高温度值相差反而不大.

(3) 油膜微倾斜参数对油膜平均温度值影响不大，但对油膜最高温度值影响很大，且顺流侧的最高温度值较逆流侧最高温度值大较多，且随着倾斜度增加其差值逐渐增大，不同微倾斜参数下的各工况油膜平均温升约5 K，最薄油膜处的油膜最高温升约14 K.