基于车辙试验的路面数值计算加载方式研究

李飞林

(广西壮族自治区高速公路发展中心，广西 南宁 530022)

0 引言

据统计，截至2021年年底，我国高速公路总里程已经达到17万km，其中沥青路面结构形式占比高达95%以上，已成为我国目前公路运营阶段中最常见的高等级路面形式。而沥青路面由于其材料的粘弹特性在高温与重载的耦合作用下易产生车辙病害，其不仅影响了驾驶人的行驶体验，对行车安全产生危害，也影响了路面的使用寿命。因此，针对新建沥青路面高温抗车辙性能的研究一直是从业者关注的重点。现行规范《公路工程沥青及沥青混合料试验规程》(JTG E20-2011)中沥青混合料车辙试验是评价沥青混凝土路面高温稳定性的主要方式。然而，沥青混凝土路面在使用过程中受温度、行车荷载等多种因素共同作用，其路面车辙病害往往会出现与室内车辙试验不相符的情况[1-2]。单一采用车辙试验评价混合料高温性能并不能反映材料真实工况下的路用性能，但通过计算机仿真技术可以消除以上因素的制约。本文通过研究不同加载方式对车辙试样的数值模拟效果，对室内车辙试验进行仿真计算，旨在获取更合理更接近实际受力工况的加载方式，对后期实际应用的模拟具有一定的参考意义。

1 试验研究

1.1 原材料及油石比

试验采用实际工程中较常用的沥青上面层SMA-10结构形式，沥青采用高弹改性沥青，粗集料为玄武岩碎石，细集料由石灰岩加工而成，矿粉为石灰石磨细矿粉，纤维为聚酯纤维。相应指标见表1～4。

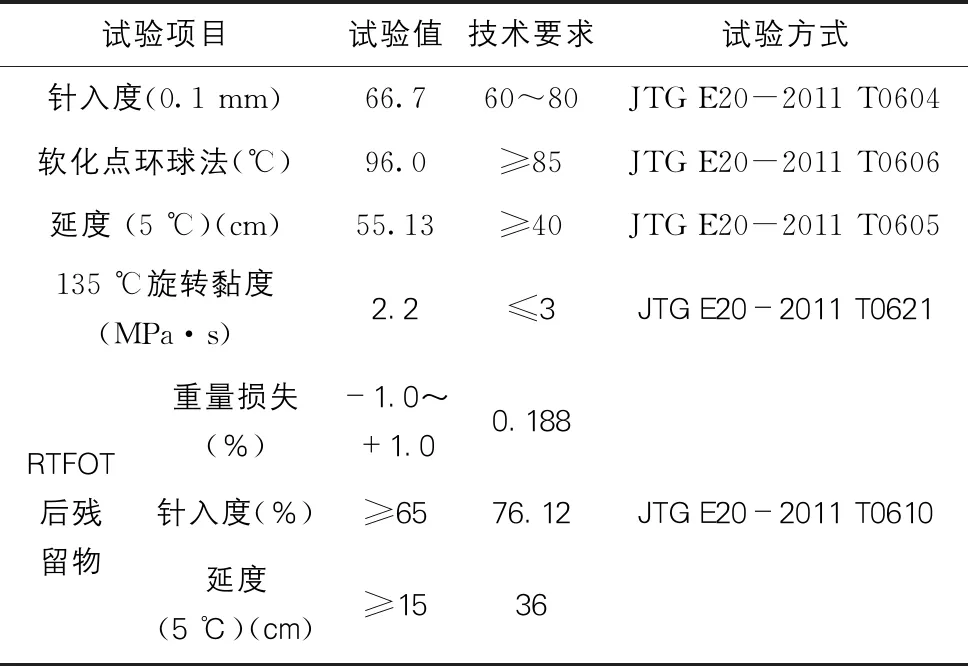
表1 高弹改性沥青基本物理指标表

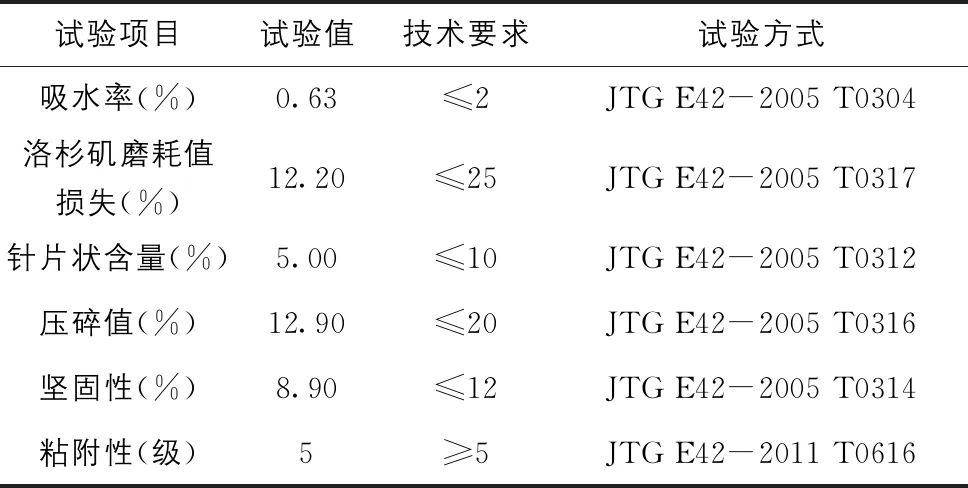
表2 粗集料主要性能指标表

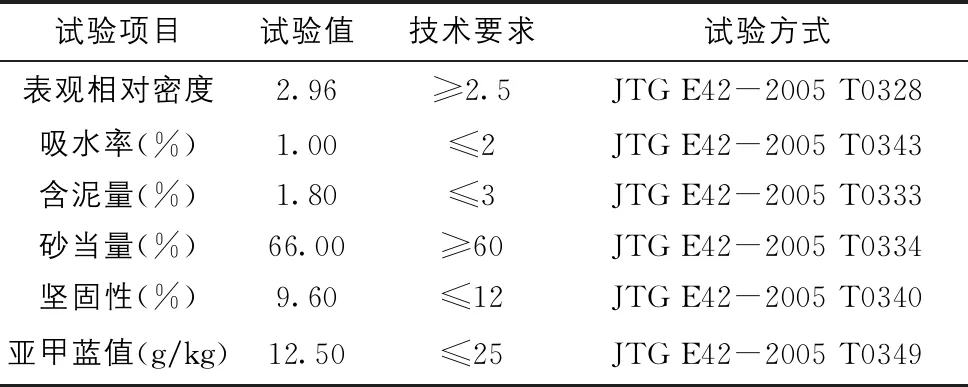
表3 细集料主要性能指标表

表4 矿粉基本物理特性数值表

根据粗细集料筛分通过率，得到SMA-10合成级配，见图1。

图1 SMA-10级配曲线图

1.2 试验准备

采用轮碾法成型300 mm×300 mm×50 mm的车辙试块，在常温环境下静置48 h。试验前试件在恒温室60 ℃保温8 h，再将试样在温度为60 ℃、轮压为0.7 MPa的条件下对试样进行车辙试验。为降低试验数据的变异性，提高精确度，进行三次平行试验，分别命名为平行试验A、B、C，将三组试验数据及其平均值变化曲线绘图，如图2所示。

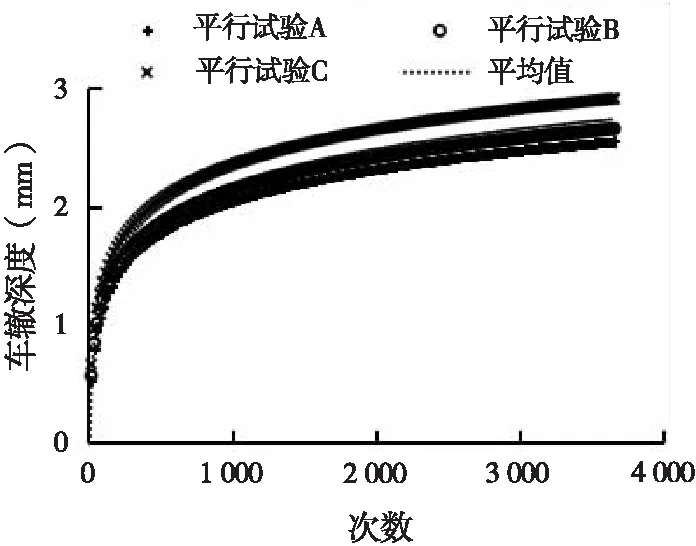
图2 车辙试验数据曲线图

1.3 试验结果

根据规范要求[3]，动稳定度应按式(1)计算：

(1)

式中：DS——沥青混合料动稳定度(次/mm);

d1、d2——通常对应试验进行45 min、60 min时的变形量(mm)；

C1——试验及类型系数，取1.0；

C2——试件系数，本试验取1.0；

N——往返碾压速度，通常为42次/min。

根据计算结果可知，三组车辙试验动稳定度最大值与最小值相差9%，小于规范规定的20%，试验合格。采用其平均值作为动稳定度，结果如表5所示。

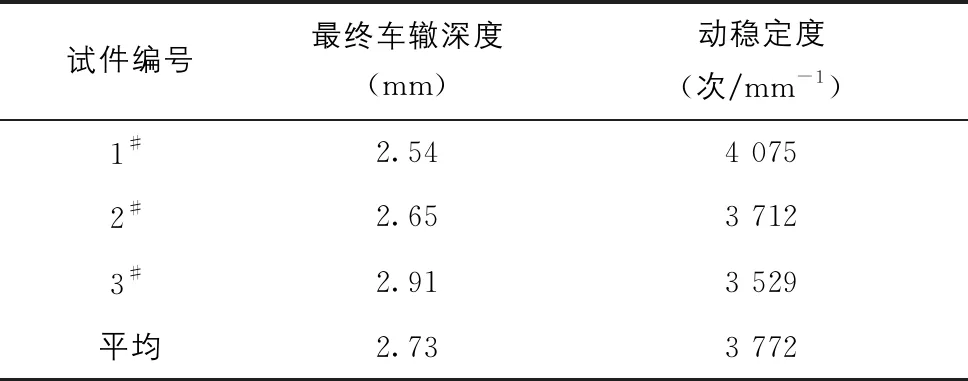
表5 三组沥青混合料车辙试验结果表

2 数值计算

2.1 加载方式

目前国内外在沥青混合料车辙试验中采用的加载方式大致可归类为三种，分别是以静代动法、等效荷载法、实际频率加载法。

2.1.1 以静代动法

该方式认为车辙成因为恒定荷载加载引起的蠕变变形，为此，可将实际多次重复加载等效为累积加载[4-5]。计算公式为：

T总=NT0

(2)

式中：T总——有限元中加载时间；

T0——加载一次的等效静载时间；

N——加载总作用次数，即60×42=2 520。

其中，换算轮载作用于车辙板上的矩形分布荷载图形长度为：

则单次静载作用时间为：

根据式(2)计算的加载作用时间为549.36 s。

2.1.2 等效荷载法

该方式以冲量守恒原则，把车辙试验作用时间看作一恒载作用[6]，其认为轮载加载形式为正弦波形式，转化原理见下页图3。

计算等效荷载为：

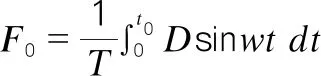
萆薢分清丸联合左氧氟沙星在多重耐药菌尿路感染中的治疗效果…………………… 尹小燕 朱健 范玉丽 等（2）218

(3)

图3 等效荷载转化示意图

式中：F0——等效静载；

T——荷载作用周期，取60 s/42 s；

t0——轮载作用时间，取22.6/v=22.6/(230/T)=161 mm/s；

D——正弦荷载幅值，取0.70 MPa；

ω——荷载作用频率，取1/T。

经式(3)计算，等效荷载为0.22 MPa。

2.1.3 实际频率加载法

按照实际加载方式施加于有限元模型中，根据相关研究成果，当荷载距某一点的距离超过6r时，荷载对该点不产生影响[6-7]，则轮载作用时间可表示为：

(4)

式中：V——速度；

r——轮胎接触半径；

t——荷载作用单次时间。

试验过程见图4(a)，试验轮从A点开始碾压至E点，距离为230 mm。轮行至B点对关注点C开始产生影响，根据式(4)，BD距离为12r=51 mm，其中包括轮载接地长度22.6 mm，AB及DE段长度为(230-51)/2=89.5 mm。整个加载过程可看成梯形波加载，如图4(b)所示。

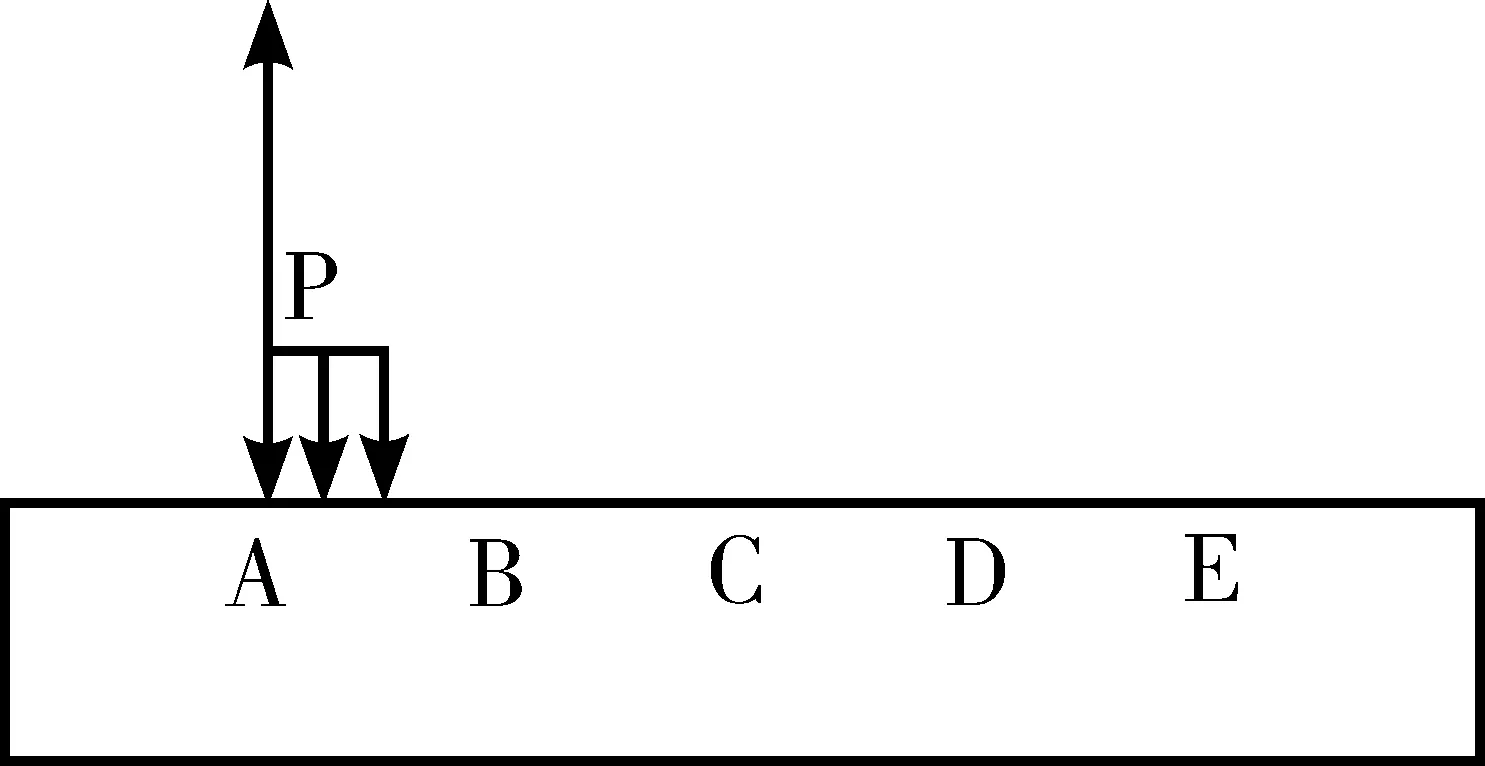
(a)车辙试验

(b)荷载作用形式

因车辙试验采用动态加载的过程，为方便后续数据处理，需对碾压过程进行简化：将单次碾压长度五等分(如图5所示)，AB1=B1B2=D2D1=D1E=46 mm，利用面积等效原理，图5所示的梯形面积与新形成的梯形B1B2D2D1面积相等，则简化后的压力为：P1=0.471 7 MPa。

图5 荷载简化示意图

2.2 计算模型

建立有限元模型时，为避免材料差异对模型结果造成影响，采用与车辙试验相同的材料同步进行单轴3 600 s蠕变试验，基于修正burgers[8]本构模型对蠕变试验数据进行拟合，得到的物理参数转化为prony级数[9]以方便有限元计算。有限元参数见表6。

表6 有限元参数表

由于车辙试验试件高度比长度小，可将其视为平面应变模型。为减小模型占用的计算内存与时间，将车辙试验简化为二维平面模型，建立尺寸为300 mm×50 mm的二维车辙试验模型，单元类型为plane182。为保证结果的准确性，在靠近加载区域对网格进行局部加密。其有限元模型如图6所示。

图6 三维车辙试验模型图

3 结果分析

对三种不同加载方式下的最终变形量和动稳定度作为比较参数进行分析。由于以静代动法加载时间与实际时间不同，对该方式加载时间在60 min内等比例线性扩大。三种不同加载方式在45 min及60 min的变形量及动稳定度的计算结果见表7及图7。

表7 计算结果与试验值对比表

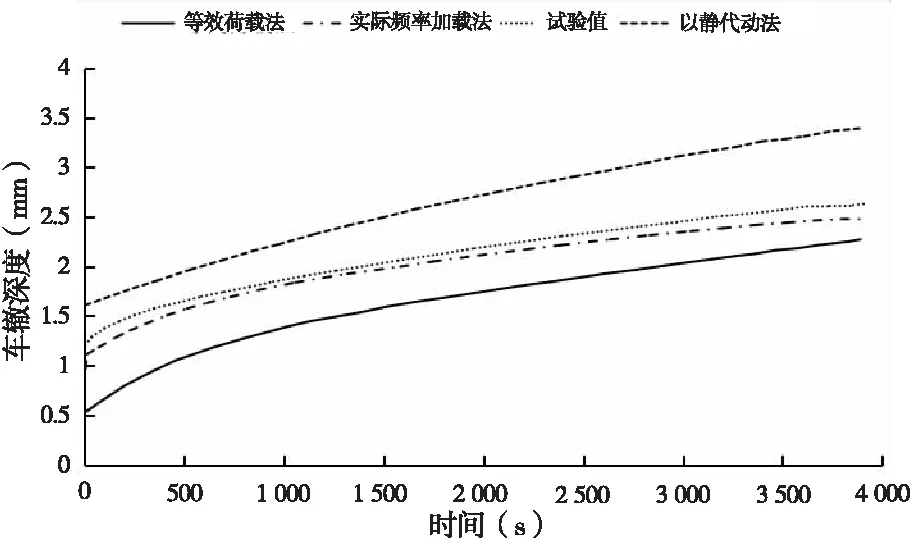
图7 计算结果与试验结果对比曲线图

由表7、图7可知：

(1)采用以静代动法模拟计算获得的最终变形量比室内车辙试验结果大24.2%，动稳定度比室内试验结果小37.9%。分析认为：由于模拟计算时加载时间比室内

试验时间短，沥青混合料蠕变尚处于“上升”阶段，变形斜率较大，而以静代动法简化了沥青混合料加载初期蠕变过程，以恒定持续加载代替了动荷载作用，加剧了沥青混合料的变形。

(2)采用等效荷载法模拟计算获得的最终变形量比室内车辙试验结果小16.8%，动稳定度比室内试验结果小22.8%。分析认为：采用等效荷载法时，由于是持续加载，不能反映实际试验过程中卸载阶段的材料蠕变恢复，因此在45～60 min时变形增长较快，因此动稳定度值比试验值小。

(3)采用实际频率加载法模拟计算的最终变形量较试验值大9.1%，动稳定度比试验值大12.2%。该方式计算的最终变形量与动稳定度值均在合理范围内，说明采用实际频率加载法可有效反映沥青混合料变形特性，在不具备试验条件的情况下可采用该方式模拟常规车辙试验加载结果。

4 结语

本文通过对三种不同车辙试验加载方式进行有限元模拟试验，对比实际车辙试验数据，得出以下结论：

(1)采用以静代动法对SMA-10沥青混合料车辙拟合效果较差，其最终变形量和动稳定度值与试验值差异分别高达24.2%、37.9%;采用等效荷载法模拟计算的最终变形量与试验值差异<20%;采用实际频率加载法模拟计算的最终变形量和动稳定度值与实际试验值均有较好的拟合效果。

(2)建议当关注车辙试验变形量时，可采用等效荷载法；分析试件车辙动稳定度时，采用实际频率加载方式更加合理。