基于Mindlin解的隧道施工引发的附加荷载及接收井变形分析

傅鹤林，张凯源，邓皇适，陈足

(中南大学 土木工程学院，湖南 长沙，410075)

在城市盾构隧道工程中，盾构机的始发、接收以及调头等工序通常在接收井或者始发井中进行，特别是盾构隧道埋深较大或位于城市内时，始发(接收)井具有占地面积小和对周边环境扰动小等特点，故其被广泛运用于盾构机始发及接收工作。随着地铁的大力建设，盾构隧道的接收基坑开挖深度及平面尺寸越来越大，难度也越来越明显，如何保证其安全性也成为众多学者研究的重点。

孙凯等[1]根据滑动体力学模型和竖向弹性地基梁模型进行了深基坑支护结构设计，并对施工进行动态数值模拟，验证了围护结构的受力和变形特征。徐中华等[2]通过收集上海地区93 个采用地下连续墙作为围护结构的工程实例，研究了支撑结构对基坑变形的影响。俞建霖等[3]采用有限元法研究了基坑围护结构在开挖时的变形特征及主要影响因素。FINNO等[4]通过对150个深基坑的变形模拟，得出了影响基坑变形的主要因素，并提出了规则长方形基坑的周边沉降空间分布模型。尹盛斌等[5]通过对基坑开挖过程的有限元数值模拟，得到了围护结构在不同受力特征下的基坑外地表沉降分布曲线。VERRUIJT 等[6-8]依据Peck 公式，结合大量的实际工程监测资料进行分析总结，得出了盾构隧道地表变形的弹性解。邓皇适等[9]根据Mindlin 解得出注浆压力空间非均匀分布引发的地表沉降计算公式并对比现场监测数据验证其适用性。倪小东等[10]结合现场监测信息分析基坑变形诱因，并建立参数弱化模型验证，得出影响基坑变形的不利因素。在现有研究中，人们主要对盾构施工对周围地表或临近建筑物的影响进行了研究[11-12]，而针对盾构机接收过程中对接收井变形的影响研究较少。若盾构机在临近接收井的过程中引起接收井变形过大，则可能导致支撑结构移位脱空甚至发生失稳破坏，因此，必须确定盾构机各施工因素对接收井受力及变形影响。

1 附加应力公式推导

在盾构施工中，扰动周边环境的主要因素有盾构机附加推力、盾壳与周边土体的摩阻力、盾尾附加注浆压力等。针对上述因素引起的周边环境扰动，本文基于Mindlin 解进行计算和分析。Mindlin 解可反映某点在水平或竖向荷载作用下引起半无限体内其他点的应力及位移变化情况。Mindlin 解力学模型简明，计算所需确定的参数数量较少[13]，童星等[14-18]用其研究土体内开挖对周边土体的扰动情况并验证了其可靠性。本文基于Mindlin 解，推导盾构施工引发周边环境的附加应力计算公式，分析盾构前方土体断面的附加应力分布情况，进而推出盾构施工引发的接收井变化情况。

Mindlin解的计算模型如图1所示。图1中，整个范围为半无限空间体，荷载作用点的坐标为(ε，η，ζ)，半无限体内任意一点的坐标为(ε0，η0，ζ0)。在荷载作用点分别施加沿x方向的水平向荷载Ph和竖直向荷载Pv。在施工过程中，接收井变形主要以水平方向即x方向的变形为主，因此，在公式推导中推导x方向的应力。

图1 Mindlin解示意图Fig.1 Mindlin's solution schematic diagram

在点M(ε，η，ζ)施加竖向荷载Pv及水平荷载Ph引起点M0(ε0，η0，ζ0)分别产生沿x方向的正应力σv和σh，其计算公式为

基于式(1)和(2)分别推导在盾构机施工中盾构掌子面附加推力、盾壳两侧与周边土体的摩擦力、盾尾处附加注浆压力引发的附加应力计算公式。

盾构掌子面附加推力相当于在刀盘面上施加水平方向荷载，单位作用面积为drdθ，刀盘中心点坐标为(0，0，H)，刀盘半径为R，如图2所示。

图2 附加推力计算模型Fig.2 Calculation model of additional thrust

假定盾构机在掘进过程中轴线偏移量较小，即盾构机沿x方向直线掘进，且盾构机推力在刀盘上均匀分布，作用点坐标为(0,Rcosθ,H-Rsinθ)，θ为作用点与水平面夹角。根据式(2)对盾构掌子面附加推力积分可得作用于周边某点(ε0，η0，ζ0)的附加应力σp为

盾壳摩阻力相当于在盾壳上作用的水平方向荷载，单位作用面积为Rdsdθ，如图3所示。

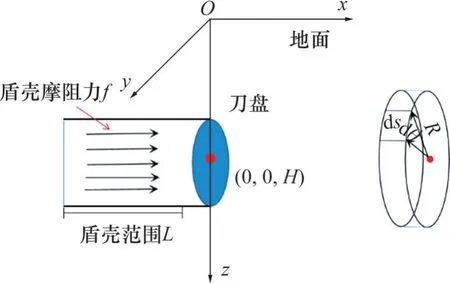
图3 摩阻力计算模型Fig.3 Calculation model of friction

假定盾壳与周边土体的摩阻力均匀分布，作用点坐标为(s,Rcosθ,H-Rsinθ)。根据式(2)对盾壳摩阻力积分可得作用于周边某点(ε0，η0，ζ0)的附加应力σf为

盾尾处附加注浆压力相当于在盾尾作用沿管片法向的作用力，单位作用面积可分解为水平方向Rcosθdadθ及竖直方向Rsinθdadθ，单环管片长度为l，如图4所示。

图4 附加注浆压力计算模型Fig.4 Calculation model of additional grouting pressure

假定注浆压力均匀分布，作用点坐标为(a-L,Rcosθ,H-Rsinθ)，水平方向作用力沿y轴方向。将式(2)的两坐标轴转换后再积分，得到盾尾注浆压力水平方向引起周边某点(ε0，η0，ζ0)的附加应力σq1为

根据式(1)对盾尾注浆压力竖直方向积分可得附加应力σq2为

在盾构施工过程中，掌子面附加推力、盾壳摩阻力以及盾尾注浆压力引起的周边地层任意一点的附加应力σx为

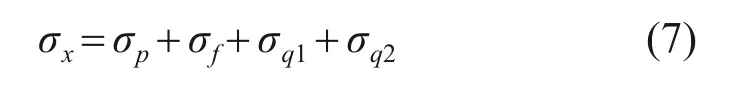
2 接收井变形计算模型

本文主要研究盾构施工对接收井的变形情况，计算得到盾构施工引起的围护结构的附加荷载，再将其施加到围护结构上得到围护结构的变形情况。接收井一般采用地下连续墙作为围护结构[16]，本文采用竖向地基梁法对盾构施工各因素进行分析计算。计算模型采用两层支撑结构，将围护结构视为由2 个不可变形支承支撑的梁体即两端铰接。本文采用的模型见图5。

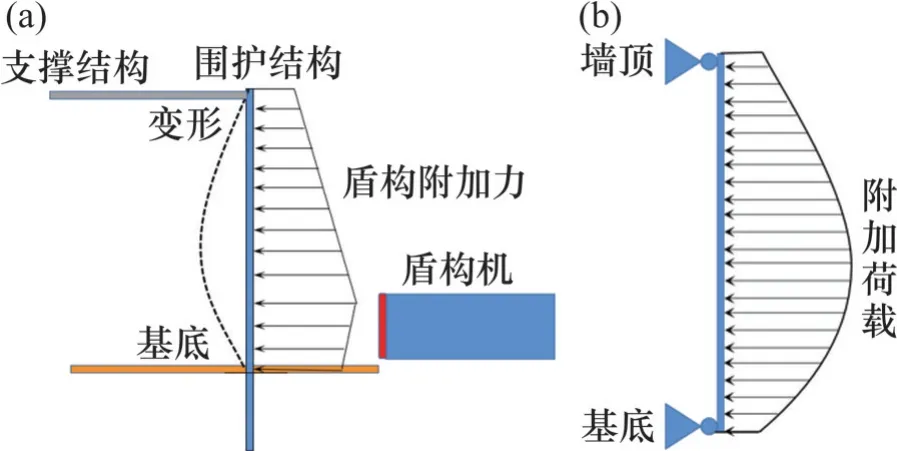
图5 变形计算模型Fig.5 Calculation models of deformation

3 理论公式计算结果及分析

以某地铁盾构施工工程为背景，隧道拱顶埋深为12.4～14.2 m，管片宽度l为1.5 m，盾壳长度L为5.0 m，接收井区域面积为10.0 m×20.0 m，围护结构采用C30现浇地下连续墙支护，混凝土支撑与围护结构连接稳固，不发生相对移动。盾构机及接收井尺寸位置关系见图6及图7。

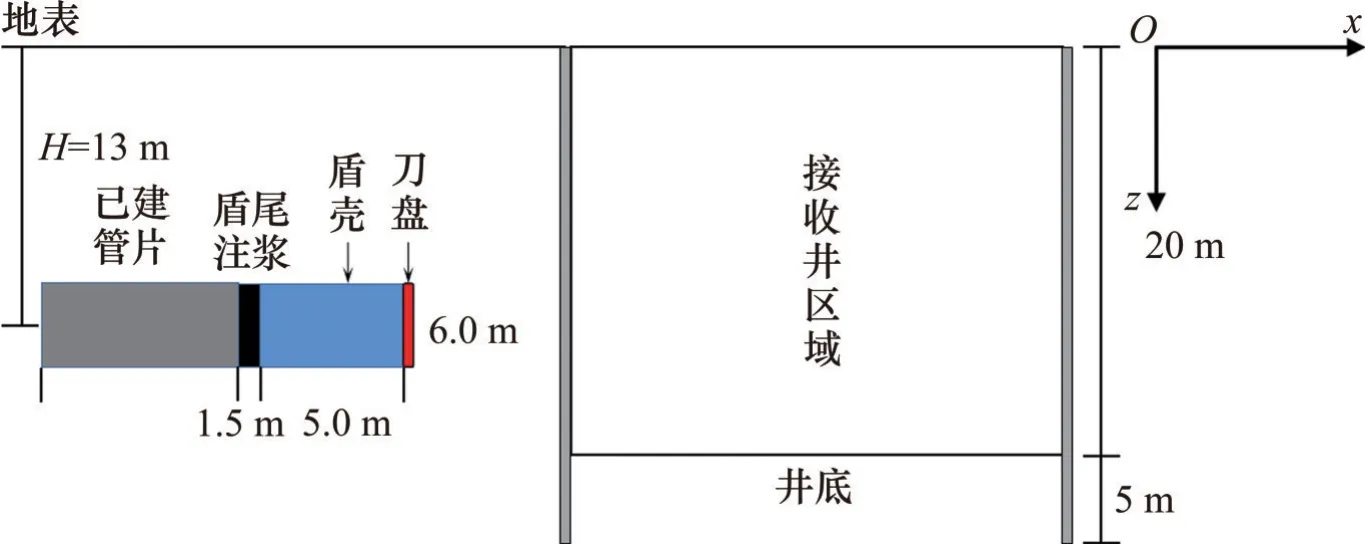
图6 盾构机与接收井纵断面图Fig.6 Longitudinal section view of shield machine and receiving shaft

图7 盾构机与接收井俯视面图Fig.7 Top view of shield machine and receiving well

土体强度参数及各施工参数由区域内土体的平均参数综合确定，各计算参数见表1。

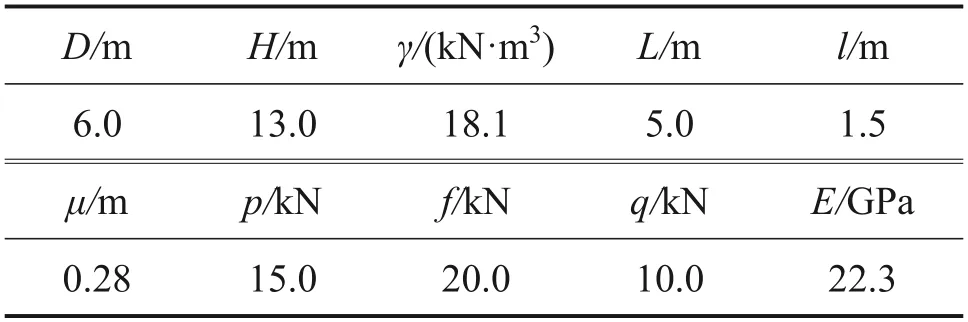
表1 计算参数Table 1 Calculation parameters

本文采用MATLAB构建5点Gauss-Legendre数值积分函数，将式(3)～(6)作为输入函数，分别计算出当盾构机刀盘距离接收井侧墙5，10，20和30 m时，各施工因素导致H=13 m 处周边100 m 区域范围内的附加荷载。

图8(a)所示为附加推力引发的附加荷载在y方向的分布情况。从图8(a)可见：在掌子面上距隧道轴线越远，附加推力引发的附加荷载越小；在隧道轴线左右两侧10 m 范围内的附加荷载较大，当距离大于10 m 时，附加荷载明显减小；附加荷载随着盾构机掌子面与围护结构的距离减小而增大，当掌子面与围护结构距离从10 m 减以到5 m 时，附加荷载增幅约200%，随着掌子面与围护结构的距离减小，附加推力引发的附加荷载更大。图8(b)所示为附加推力引发的附加荷载在x方向的分布情况。从图8(b)可见：附加推力引起的附加荷载在x方向以刀盘平面为对称中心呈反对称分布，即附加推力对刀盘平面土层不会产生附加荷载；盾构机刀盘在不同位置引起的附加荷载的最大值基本一致。

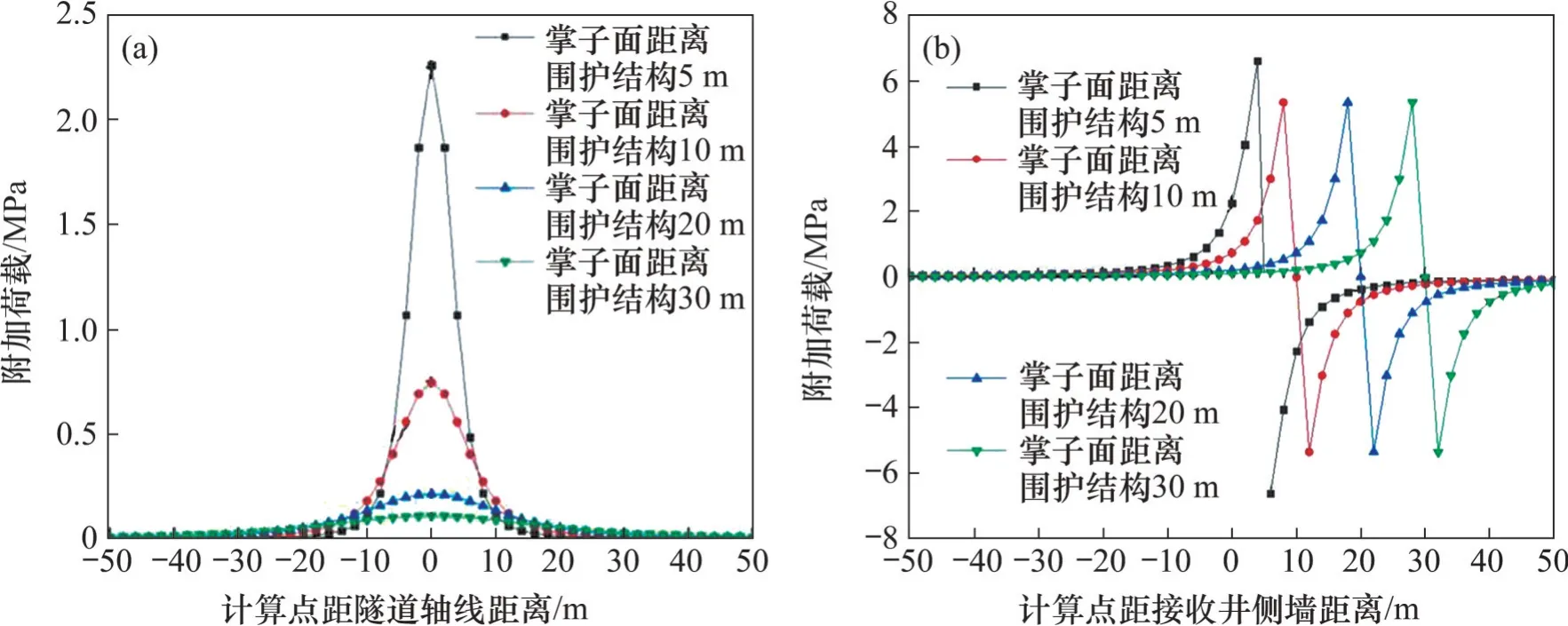
图8 附加推力引发的附加荷载Fig.8 Additional load caused by additional thrust

图9 所示为盾壳摩阻力作用下y和x方向的附加荷载。从图9(a)可见：盾壳摩阻力的附加荷载在y方向的值比附加推力引发的更大，这是由于盾壳摩阻力的作用范围及大小比附加推力的大；当掌子面距围护结构的距离为5 m时，在隧道轴线处附加荷载突然减小，这是由于盾壳两侧的环状摩阻力在接近围护结构时，对围护结构上环状区域的影响逐渐减弱；从图9(b)可见，盾壳摩阻力的附加荷载在x方向的分布情况与附加推力引发的附加荷载的分布情况基本一致，都是以盾壳中线为对称中心呈反对称分布，但范围比附加推力的分布范围更宽。由于盾壳前半部分产生的反向荷载与后半部分产生正向荷载叠加，导致此截面附加荷载为0。

图9 盾壳摩阻力引发的附加荷载Fig.9 Additional load caused by the friction of the shield shell

图10所示为附加注浆压力作用下y和x方向附加荷载，在y方向呈非对称分布，最大值约在注浆位置处，且相比于其他因素影响基本可以忽略；附加注浆压力影响范围在注浆位置前后三环管片内，在掌子面前方影响极小。

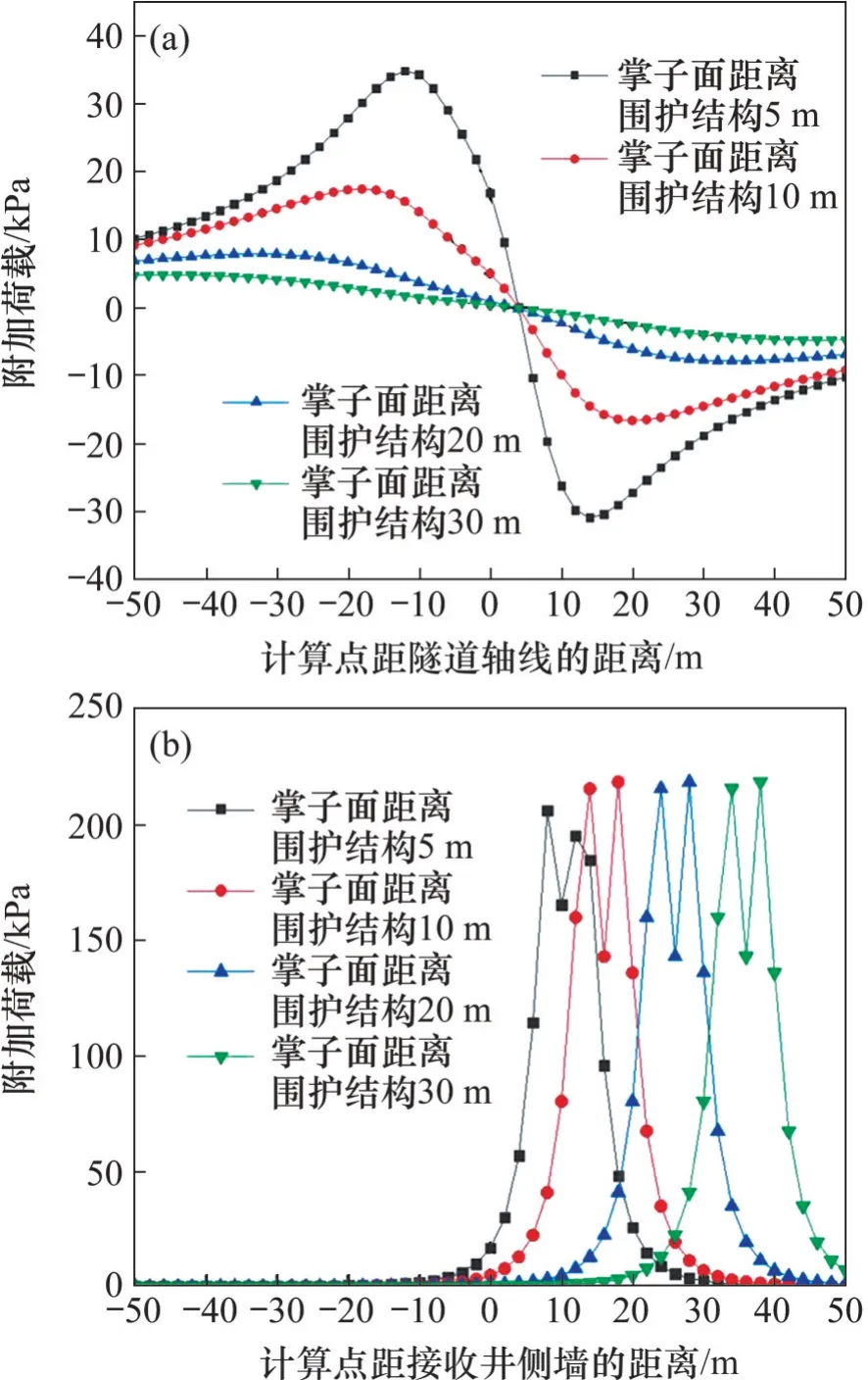
图10 附加注浆压力引发的附加荷载Fig.10 Additional load caused by additional grouting pressure

改变计算点深度，研究深度及盾构机距离对附加荷载的影响。取计算点深度变化范围为0～30 m，接收井侧墙与盾构机刀盘距离为5，10，20和30 m，计算得到y=0 m时盾构刀盘附加推力、盾壳摩阻力以及盾尾附加注浆压力引发的附加荷载。

图11 所示为附加推力作用下附加荷载沿深度方向的变化情况。从图11 可见：附加荷载沿深度方向先增加后减小，最大值在刀盘中心处；附加荷载随盾构机刀盘与围护结构的距离减少而显著增加。

图11 附加推力引发的附加荷载Fig.11 Additional load caused by additional grouting pressure

图12 所示为盾壳摩阻力作用下附加荷载沿深度方向变化情况。从图12 可见：与掌子面附加推力的分布规律基本一致，在盾构机刀盘中心点位置处的附加荷载达到最大值；随着盾构机接近围护结构，在围护结构中心产生突变，这是由于环状的盾壳摩阻力与围护结构上环状中心距离不断减小，影响也逐渐减弱；盾壳摩阻力导致的附加荷载明显大于掌子面附加推力产生的附加荷载。

图12 盾壳摩阻力引发的附加荷载Fig.12 Additional load caused by the friction of shield shell

图13 所示为附加注浆压力作用下附加荷载沿深度方向变化情况。从图13 可见：附加荷载近似以刀盘中心深度为对称点呈反对称分布，附加荷载随着盾构机刀盘与围护结构的距离减小而增大，但与附加推力和盾壳摩阻力相比可以忽略不计。

图13 注浆压力引发的附加荷载Fig.13 Additional load caused by grouting pressure

将掌子面附件推力、盾壳摩阻力以及附加注浆压力引起的附加荷载叠加，计算接收井侧墙与盾构机刀盘距离为5 m 和20 m 时，围护结构在y=0 m处的变形。

图14 所示为接收井侧墙中线y=0 m 处的变形情况。从图14 可见：产生变形的主要因素是盾壳摩阻力，其次是附加推力，附加注浆压力对围护结构变形的影响较小；当刀盘距围护结构5 m 时，围护结构的最大变形约为18 mm，位移较大，可能会导致支撑结构失效，发生脱落，影响基坑的整体稳定性；变形在刀盘的环状范围内产生突变，与盾壳摩阻力引起的附加荷载分布情况一致；当刀盘距围护结构20 m 时，围护结构的最大变形仅为0.8 mm，说明当盾构机距离围护结构较远时，对围护结构的影响很小，基本可以忽略。

图14 接收井侧墙中线处变形情况Fig.14 Deformation at the center line of the side wall of the receiving well

4 数值模拟

通过数值模拟对理论结果进行验证，使用Midas GTS得出单线隧道分析盾构掘进中接收井侧墙的变形，如图15所示。

图15 单线盾构隧道临近接收井模型Fig.15 Single-line shield tunnel near the receiving shaft model

随着盾构掘进，接收井侧墙在y=0处的最大变形见图16。从图16可见：当盾构机掘进40 m即刀盘距围护结构10 m 时，最大变形开始剧增，约占总变形的80%；在盾构临近接收井时，需要调整盾构机推力、掘进速度等参数以保证接收井围护结构的稳定性；在模拟过程中，当盾构机刀盘距围护结构5 m 时，最大变形(约22 mm)与理论计算结果(18 mm)误差较小，验证了理论计算结果的正确性和适用性。

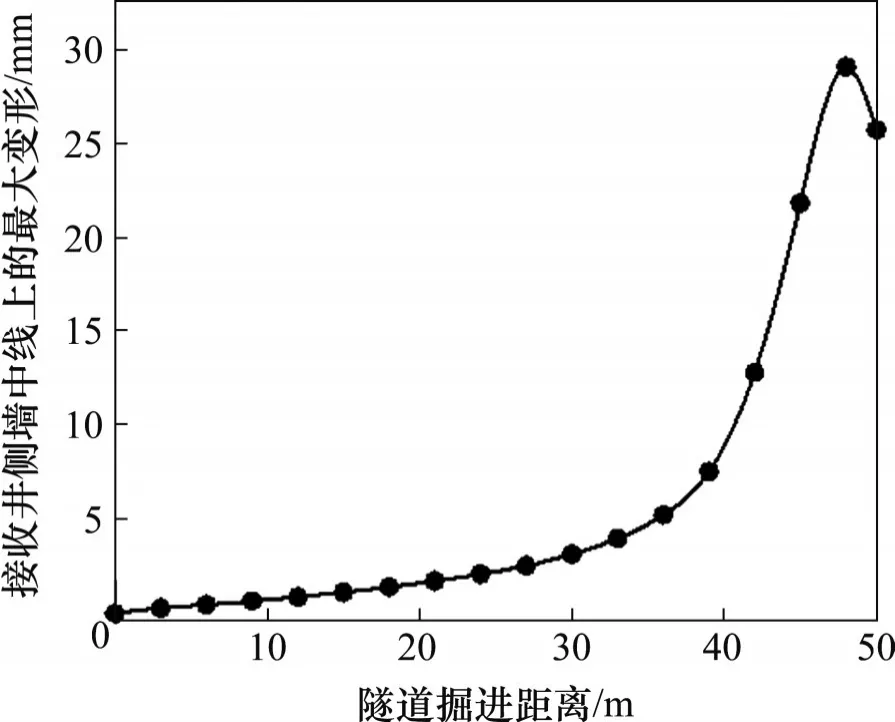
图16 接收井侧墙中线处最大变形Fig.16 The maximum deformation at the center line of the side wall of the receiving well

当盾构机刀盘距离接收井侧墙10 m和5 m时，对y=0 m处接收井的变形云图进行分析并对变形数值模拟结果与理论计算结果进行对比，分别如图17和图18所示。从图17和图18可见：围护结构变形数值模拟结果与理论结果在大小和变化趋势上大致相似，数值模拟结果偏大，且在距离为5 m时，变形在环形范围内突变消失。其原因是：1) 理论计算中将接收井侧墙视为梁单元，而在模拟中作为板单元更接近工程实际；2) 在理论计算中，仅考虑盾构机的影响并进行弹性计算，没有将土体塑性区的形成以及对接收井的影响考虑在内。

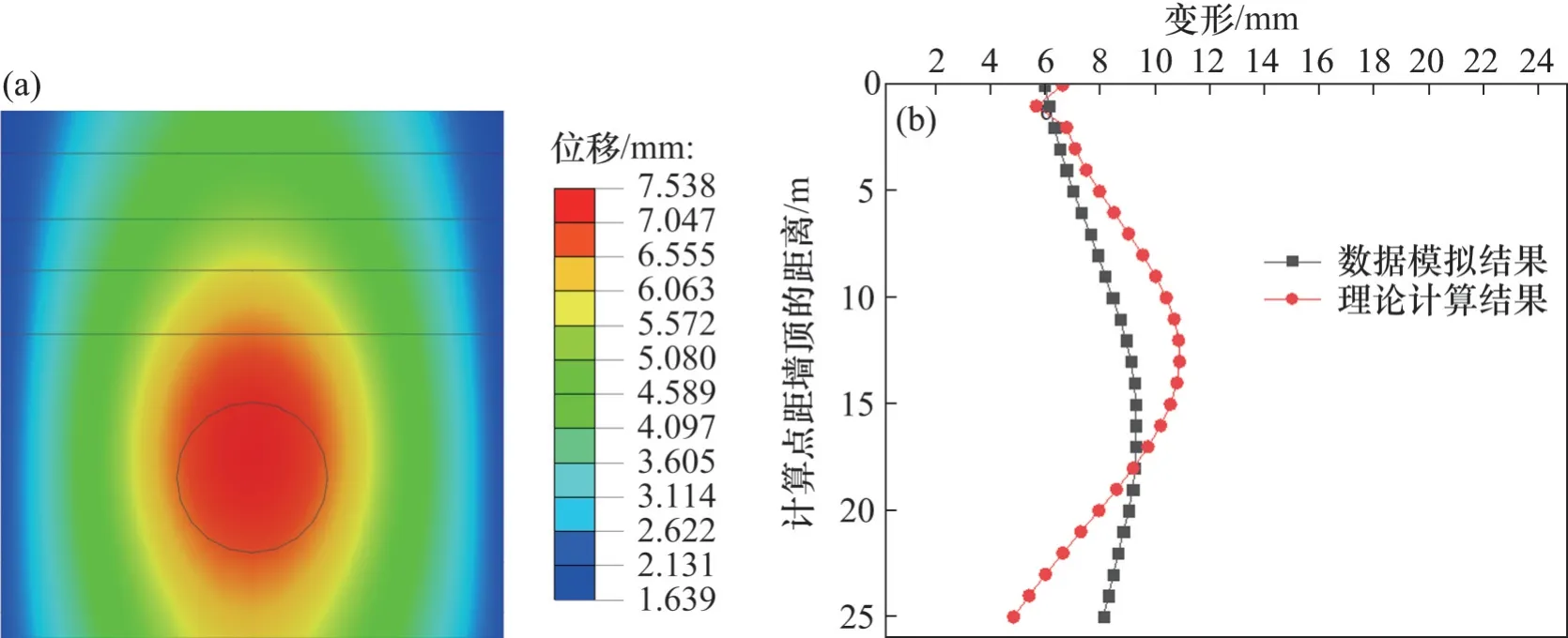
图17 刀盘距接收井10 m时接收井的变形Fig.17 Deformation of the receiving well when the cutter head is 10 m away from the receiving well

图18 刀盘距接收井5 m时接收井的变形Fig.18 Deformation of the receiving well when the cutter head is 5 m away from the receiving well

5 结论

1) 基于Mindlin解，推导了在盾构机掘进过程中，掌子面附加推力、盾壳摩阻力以及附加注浆压力对接收井围护结构产生的附加应力的计算公式；基于竖向地基梁模型，对接收井围护结构的变形进行了计算。

2) 盾壳的摩阻力导致接收井围护结构的附加荷载在埋深方向的分布规律为先增大后减小；当掌子面与围护结构距离较近时，盾壳摩阻力产生的附加荷载在刀盘中心深度产生突变，其原因是盾壳摩阻力接近围护结构时对环形中心范围影响逐渐降低；掌子面附加推力产生的附加荷载在埋深方向随深度增加先增大后减小；附加注浆压力导致接收井围护结构附加荷载在埋深方向呈反对称分布。

3) 导致接收井围护结构产生变形的主要因素为盾壳的摩阻力，其次为掌子面附加推力。盾尾附加注浆压力对围护结构产生的变形可以忽略。

4) 盾构机临近接收井时的围护结构变形比理论变形偏大，其原因是理论计算时没有考虑接收井周围土体等的因素对围护结构的影响。