一种基于DWT-HD-SVD的数字图像水印算法

张丽艳，温万钦

(大连交通大学 电气信息工程学院，辽宁 大连 116028) ①

随着互联网技术的飞速发展，数字信息的复制、传播、引用也随之泛滥，由此引发了严重的侵犯版权问题，数字知识产权的保护已成为迫切需要解决的问题.数字水印作为多媒体认证和防伪的重要工具，对数字知识产权保护有着重大的现实意义和实用价值.

目前各类水印算法主要研究水印的隐蔽性和鲁棒性问题. 李云亚等[1]探讨了当前国内外各类抗攻击的图像水印技术，随着新的攻击形式的出现，图像水印面临新的挑战，神经网络与深度学习技术在图像领域的发展使图像水印的抗攻击性能和算法的复杂程度有了改进的空间. 张帅等[2]利用图像信息熵与边缘熵的理论，确定了适合水印嵌入的分块，提高了水印的隐蔽性. 赵睿琦[3]基于DWT-SVD(离散小波变换，Discrete Wavelet Transform，DWT；奇异值分解，Singular Value Decomposition，SVD)技术提出非盲水印和盲水印两种水印算法，对提出的两种算法分别进行JPEG压缩、均值滤波、高斯噪声等攻击，该算法在较强的均值滤波和椒盐噪声攻击下的鲁棒性均表现不佳，还有很大的改进空间. 程艳艳[4]基于DCT变换对选择的子块进行分解，通过构建粒子群算法的适应度函数，迭代获取最优的嵌入强度，将水印信息隐藏到上Hessenberg矩阵中，生成水印图像，取得了理想的隐蔽性和鲁棒性.为此本文将参考文献[3-4]的方法结合起来，在文献[3]的基础上提出了一种基于DWT-HD-SVD的水印方法，增强水印的鲁棒性.

1 算法理论基础

1.1 离散小波变换

离散小波变换是一种信息保持型的可逆变换，信号的信息保留在小波变换的系数中[5].小波变换将图像分解成不同空间、不同频率的子图像，使得原图像或信号的能量重新分配，得到一种能量紧凑的图像表示方式，图像信息的局部特征可通过小波系数而改变.小波变换后可将图像划分为4个子带：低-低、低-高、高-低和高-高，图像经过一级DWT后包含的大部分信息集中到低-低子带中.

1.2 Hessenberg分解

Hessenberg分解(Hessenberg decomposition，HD)是一种矩阵分解方法，具有较低的时间复杂度，可用于方阵分解[6].利用HD分解可以得到更精确的宿主图像分量，提高嵌入水印图像的鲁棒性.对n×n的方阵X进行HD分解，见式(1)：

PHPT=HD(X)

(1)

式中：P为酉矩阵；H为上Hessenberg矩阵.假设h(i,j)表示H矩阵的元素，当i>j+1时，h(i,j)=0.HD通常由Householder正交矩阵Q计算，见式(2)：

(2)

式中：μ是Rn中的一个非零向量；In是一个n×n的单位矩阵.HD的计算见式(3)：

P=(Q1Q2…Qn-2)TX(Q1Q2…Qn-2)

⟹H=PTXP

⟹X=PHPT

(3)

1.3 奇异值分解

奇异值分解可通过对角化将矩阵中行或列的相关性保存在奇异值中[7].由于奇异值具有较高的稳定性，图像在遭受小的干扰变化时，它的奇异值基本保持稳定，这对提高数字水印算法的鲁棒性具有重要意义.另外SVD的尺度不变性使其可以对任意尺寸大小的图像矩阵进行分解.

SVD将对称矩阵分解为两个正交矩阵U、V和一个对角矩阵S，奇异值以对角阵的形式分离出来.对称矩阵Y进行SVD分解，见式(4)：

USVT=SVD(Y)

(4)

式中：S=diag(σ1,σ2,…,σr,0,…,0)，对应降序排列的奇异值系数.

2 水印方案

2.1 水印嵌入方案

在水印嵌入方案中，宿主图像C和水印图像W作为输入，嵌入水印的图像C*作为输出.该水印算法适应多种尺寸的水印图像，且宿主图像采用R级小波变换进行分解.水印的嵌入过程见图1.

图1 水印嵌入流程图

Step1：基于R级DWT将宿主图像C分解为低-低、低-高、高-低和高-高4个子带，其中R=log2(M/N).

Step2：对DWT变换得到的低-低子带进行Hessenberg分解.

PHPT=HD(LL)

(5)

Step3：对Hessenberg分解得到的H矩阵进行SVD分解.

HUwHSwHVwT=SVD(H)

(6)

Step4：将水印图像W进行SVD分解.

UwSwVwT=SVD(W)

(7)

Step5：将HSw和Sw加入一个适当的嵌入强度α，由此计算嵌入的奇异值HSw*.

HSw*=HSw+α·Sw

(8)

Step6：利用逆SVD运算构造一个新的子带H*.

H*=HUwHSw*HVwT

(9)

Step7：基于逆Hessenberg分解构造一个新的LL*.

LL*=PH*PT

(10)

Step8：执行逆R级DWT变换获得嵌入水印的图像C*.

2.2 水印提取方案

在水印提取方案中，嵌入水印的图像C*作为输入，提取到的水印W*作为输出.提取出的水印大小与原始水印大小相同.水印的提取过程见图2.

图2 水印提取流程图

Step2：对DWT变换得到的LLw子带进行Hessenberg分解.

PwHwPwT=HD(LLw)

(11)

Step3：对Hessenberg分解得到的Hw矩阵进行SVD分解.

HUw*HSbw*HVw*T=SVD(Hw)

(12)

Step4：计算提取水印所需的奇异值Sw*.

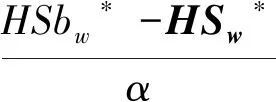
(13)

Step5：通过逆SVD分解重构提取出的水印W*.

W*=UwSw*VwT

(14)

2.3 水印评价指标

水印的隐蔽性是指原始作品与嵌入水印后的作品在视觉效果上的相似度，前后产生的变化越小隐蔽性越好[8-9].为了定量地描述隐蔽性，把嵌入的水印作为加载到载体图像上的噪声，通过图像质量评价指标——峰值信噪比(Peak Signal-to-Noise Ratio，PSNR)和结构相似性(Structural Similarity，SSIM)来评估水印算法的隐蔽性，见式(15)～式(17)：

(15)

(16)

式中：MSE表示宿主图像和嵌入水印的图像之间的均方误差；Ci,j2为宿主图像中的最大像素值.

通常情况下，水印嵌入前后峰值信噪比低于30 dB，说明水印的隐蔽性比较差，如果高于37 dB，肉眼很难看出水印嵌入前后的差别，说明水印的隐蔽性较好，总之,PSNR值越大说明隐蔽性越好[10].

(17)

式中：μC和μC*分别是C和C*的平均值；σC2和σC*2分别是C和C*的方差值；σCC*是C和C*的协方差；d1和d2是两个用来维持稳定的常数.嵌入水印的图像与宿主图像的相似度越高，SSIM值越趋近于1[11].

这几年，李敬益和社区同事在处理矛盾纠纷上又想出了新方法。他们在社区范围内发放“彩云社区无忧卡”和“彩云社区民情联系卡”。这两张卡的正面是诉求者的基本信息与诉求内容，背面是社区工作人员的手机号码。

水印的鲁棒性是指数字作品在经过某种有意或无意的处理后，嵌入的水印信息仍能保持部分完整性，并能被准确鉴别. 评估鲁棒性可利用原始水印与提取出的水印之间的归一化相关系数(Normalized Cross Correlation，NC)，见式(18).

(18)

NC值越接近 1 说明提取出的水印越接近原始水印，在未受攻击的情况下该值应该是 1，在受到攻击的情况下该值越高说明算法的鲁棒性越好.

3 算法仿真与结果分析

本文基于英特尔单核2.6 GHz的CPU和8.0 GB的RAM计算机硬件平台，Matlab R2020b软件环境，来进行仿真实验.选用512×512的Lena图像作为宿主图像，256×256、128×128、64×64的“大连交大”字样的图像作为水印，仿真中用到的图像攻击类型及规格参数见表1，其中QF为品质因数; CR为分解率 ; HE为直方图均衡化.

表1 图像攻击类型及规格参数

3.1 寻找最佳嵌入强度

在水印算法中，不同图像的嵌入强度有所差异，如果设置了最佳嵌入强度，可优化算法性能[12].本文分别对256×256、128×128、64×64 3种不同尺寸的水印图像进行测试，选取嵌入强度α的范围为[0,0.2]，以256×256的水印图像为例，不同嵌入强度下的仿填性能见图3.

(a) NC值

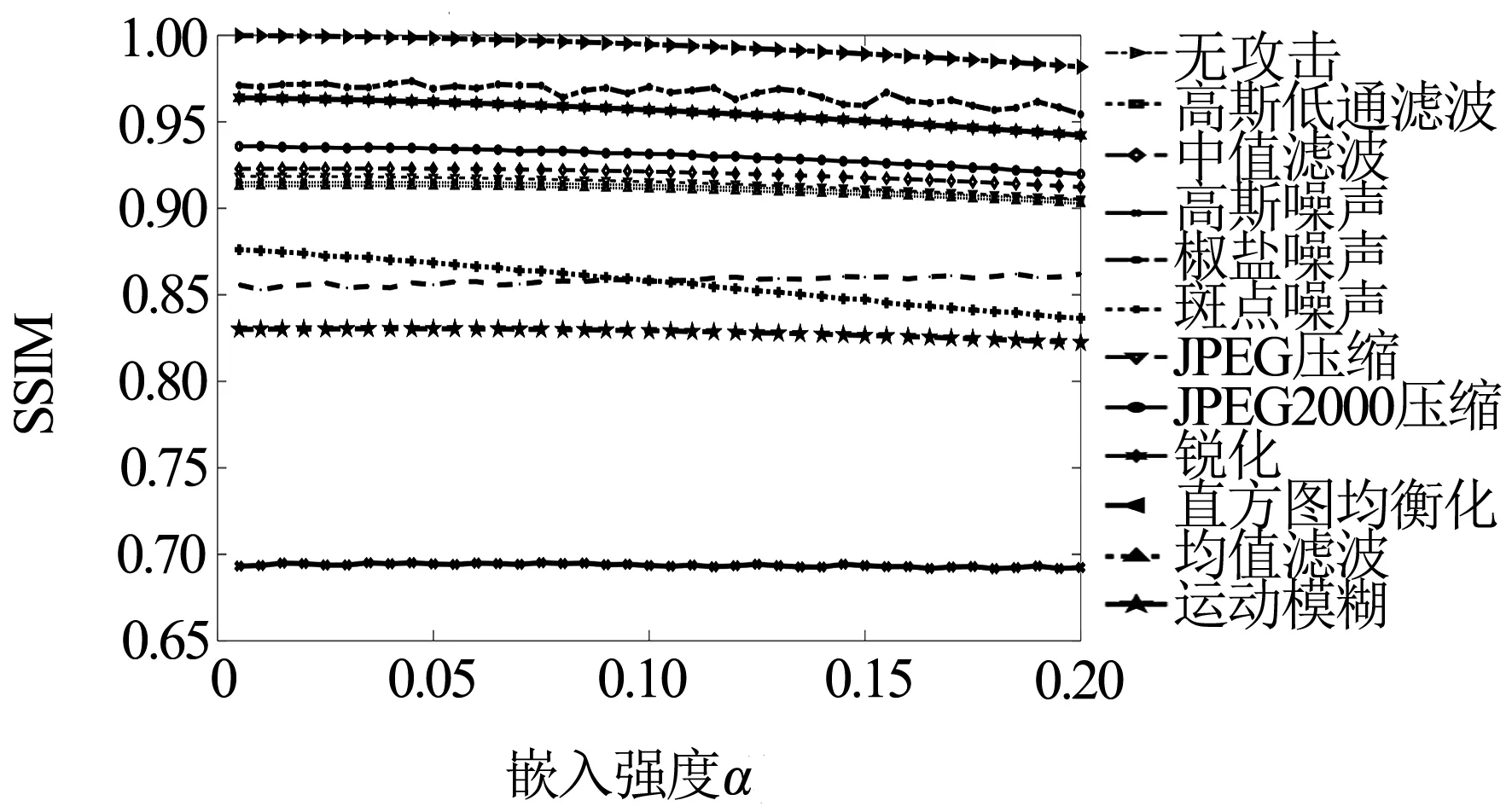
(c) SSIM值续图3 256×256水印不同嵌入强度下的仿真性能

仿真结果表明：在α的动态变化范围内，PSNR值呈递降趋势，考虑到算法的隐蔽性，取一个PSNR的适当值作为评价标准；SSIM值在α变化范围内基本维持稳定，SSIM值越大，嵌入水印的图像与宿主图像差异较小；除直方图均衡化攻击外，其余类型攻击的NC值均与α呈正相关性，嵌入强度在0.02之前增幅较大，随后逐渐趋近于1.高斯低通滤波、均值滤波和运动模糊类型的收敛速度较慢.综合3个评价指标，确定256×256、128×128、64×64 3种尺寸水印的最佳嵌入强度分别为0.05、0.10、0.12.

3.2 隐蔽性分析

水印算法的隐蔽性建立在不受攻击的基础上，嵌入后的水印必须是人眼不可见的.未受攻击的水印嵌入与提取结果见图4.仿真结果表明，该水印算法在主客观分析上均满足隐蔽性要求.

图4 未受攻击的水印嵌入与提取结果

3.3 鲁棒性分析

表2给出了在各类攻击下提取的水印质量分析结果.

表2 不同水印在不同攻击下的NC值

从表中可以看出，NC值随着水印尺寸的减小而增大，且NC值较高.此外这些攻击所提取的水印几乎在视觉上都是清晰的，即使运动模糊下提取的水印有轻微的模糊，但水印的主要信息仍然是可识别的.3种尺寸的水印在滤波、噪声、压缩和锐化攻击下，NC值均在0.985之上，表明该水印算法在这些攻击下具有良好的鲁棒性.

为了进一步验证该算法的鲁棒性，本文考虑并测试了攻击参数动态变化下的情况，见图5.

图5(a)显示了JPEG压缩攻击下不同品质因子的水印算法鲁棒性，QF越小图像被压缩的越多，即使QF=10，3种水印的NC值都高于0.995.图5(b)显示了JPEG2000压缩攻击下不同压缩强度的水印算法鲁棒性，CR越大图像压缩的越多，即使CR=36，3种水印中最差的NC值也大于0.993.图5(c)和5(d)分别测试了不同参数的高斯低通滤波和中值滤波的水印算法鲁棒性，结果表明，3种水印高斯低通滤波器的NC值均大于0.96，中值滤波NC值缓慢下降，但均大于0.945.图5(e)显示了高斯噪声攻击下不同方差参数水印算法的鲁棒性，256×256的水印NC值降幅较大.图5 (f)显示了阈值为1，不同锐化强度下水印算法的鲁棒性，3种水印的锐化攻击NC值在0.985之上.

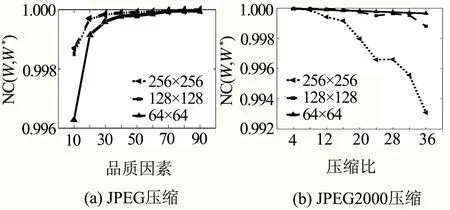
图5 3种水印不同参数攻击下的NC值

良好的NC值代表优越的鲁棒性，即使是不同大小的水印，也能抵御这几种类型的攻击，尤其是JPEG压缩、JPEG2000压缩和锐化攻击.特别是对于64×64的水印，除了JPEG压缩攻击的鲁棒性略微较低外，其他情况下的鲁棒性均优于另外两种尺寸的水印，且NC值大于0.98，因此该水印算法具有很好的隐蔽性和鲁棒性.

3.4 对比实验分析

使用相同的宿主图像和水印图像，在相同规格的攻击类型下，将本文提出的水印算法与文献[3]和文献[4]中的算法的鲁棒性做进一步对比分析，对比结果见表3.本文提出的算法在椒盐噪声、中值滤波及JPEG压缩中相比文献[3-4]的抗攻击性均表现出一定的优势.在旋转几何攻击下本文算法的性能略优于文献[3]，但不及文献[4]，还有较大的改进空间.

表3 相关文献算法与本文算法的鲁棒性对比

4 结论

本文提出了一种基于DWT-HD-SVD变换的数字图像水印算法.首先对不同尺寸水印的算法性能指标进行分析，找到适当的不同水印嵌入强度，在此基础上通过多种规格参数的模拟攻击，对该算法的隐蔽性和鲁棒性进行了仿真分析，最后与相关文献算法的鲁棒性进行了对比.实验结果表明，该算法得到的嵌入水印图像不仅具有良好的视觉质量，而且在不同的攻击下均可提取出清晰的水印图像，表现出更强的鲁棒性，即使是不同尺寸的水印，该算法也具有很好的隐蔽性和鲁棒性.