带有量子修正的Zakharov方程的精确非线性波解

吴沈辉，宋明

带有量子修正的Zakharov方程的精确非线性波解

吴沈辉，宋明*

（绍兴文理学院 数理信息学院, 浙江 绍兴 312000）

利用动力系统定性理论和分支方法，研究了带有量子修正的Zakharov方程的精确非线性波解，给出了不同参数条件下的相图，沿相图中的特殊轨道进行了积分，得到量子Zakharov方程的4个孤立波解、7个奇异波解和24个周期波解共3类非线性波解。当参数取特殊值时，对部分周期波解取极限，给出了周期波解演化为相应的孤立波解和奇异波解的过程。

分支方法；修正Zakharov方程；非线性波解

0　引言

1972年，ZAKHAROV［1］提出了可用于描述高频Langmuir波和低频等离子波之间非线性相互作用的Zakharov方程，此为等离子体物理中的重要方程组。在一维情况下，经典的Zakharov方程为

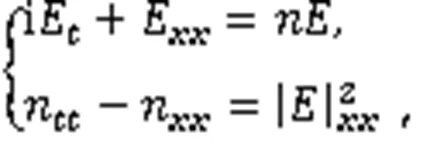
近年来，众多学者致力于研究经典等离子体中的物理现象。考虑量子效应，用经典模型进行描述不够精确，GARCIA等［2］利用量子流体方法得到带有量子修正的Zakharov方程：

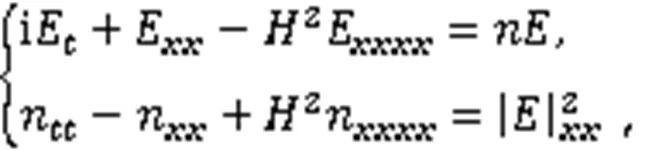
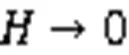
首先，利用动力系统分支方法和定性理论［10-20］研究量子Zakharov方程的非线性波解，讨论不同参数取值范围内行波解的存在性。其次，通过行波变换将方程转至平面系统，确定不同参数条件下奇点的类型，并借助Mathematica软件得到系统的分支相图，分别对相图中的同宿轨道、异宿轨道和周期轨道进行积分，得到对应的孤立波解、奇异波解和周期波解。最后，给出当参数取极限时周期波解演化为孤立波解和奇异波解的过程。

1　相图

采用变换：

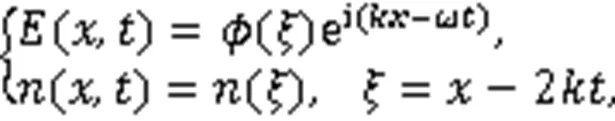
将式（2）转化为

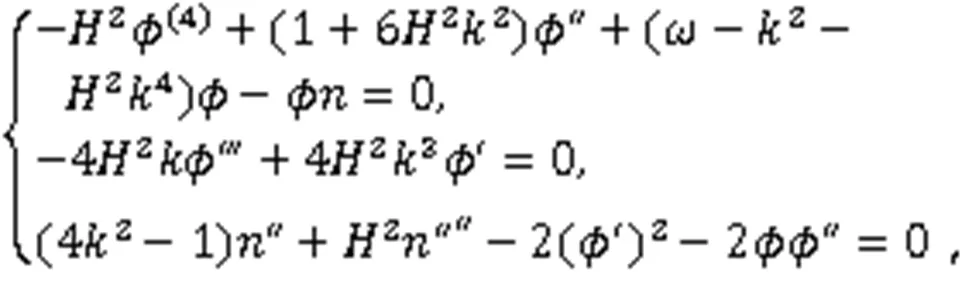
将式（4）的第2式求导后代入第1式，并对第3式积分2次，得

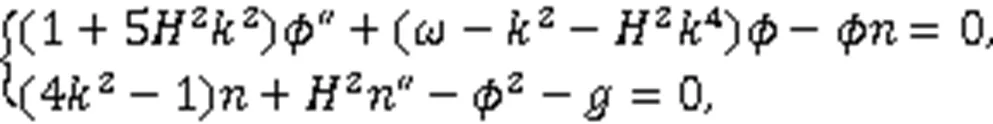
设

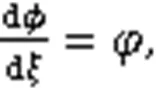
将式（6）代入式（5）的第1式，得

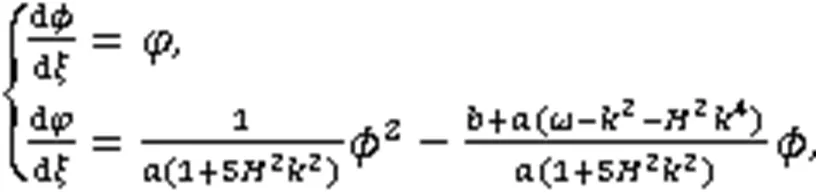
将式（6）代入式（5）的第2式，得

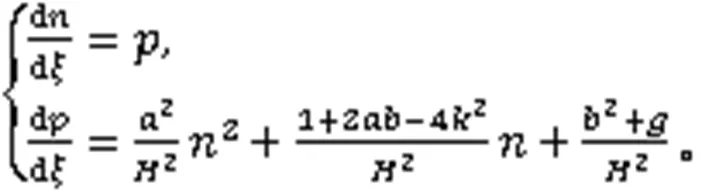
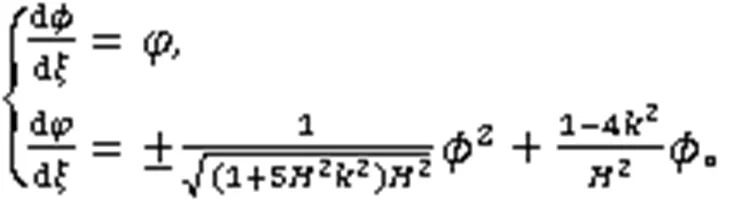
对式（9）积分，得到2个哈密顿函数：

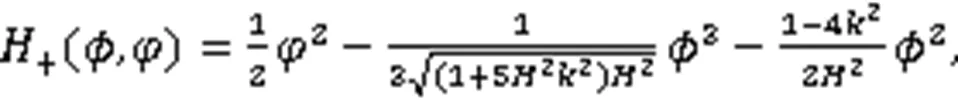
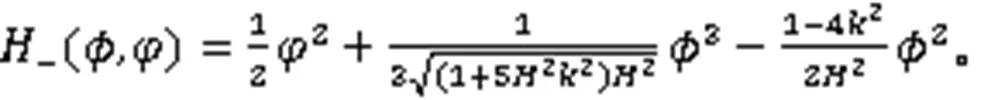
令

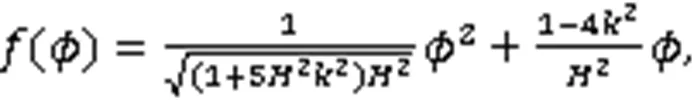
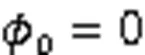
根据动力系统定性理论，利用Mathmatica软件，得到式（9）的相图（图1）。

2　非线性波解

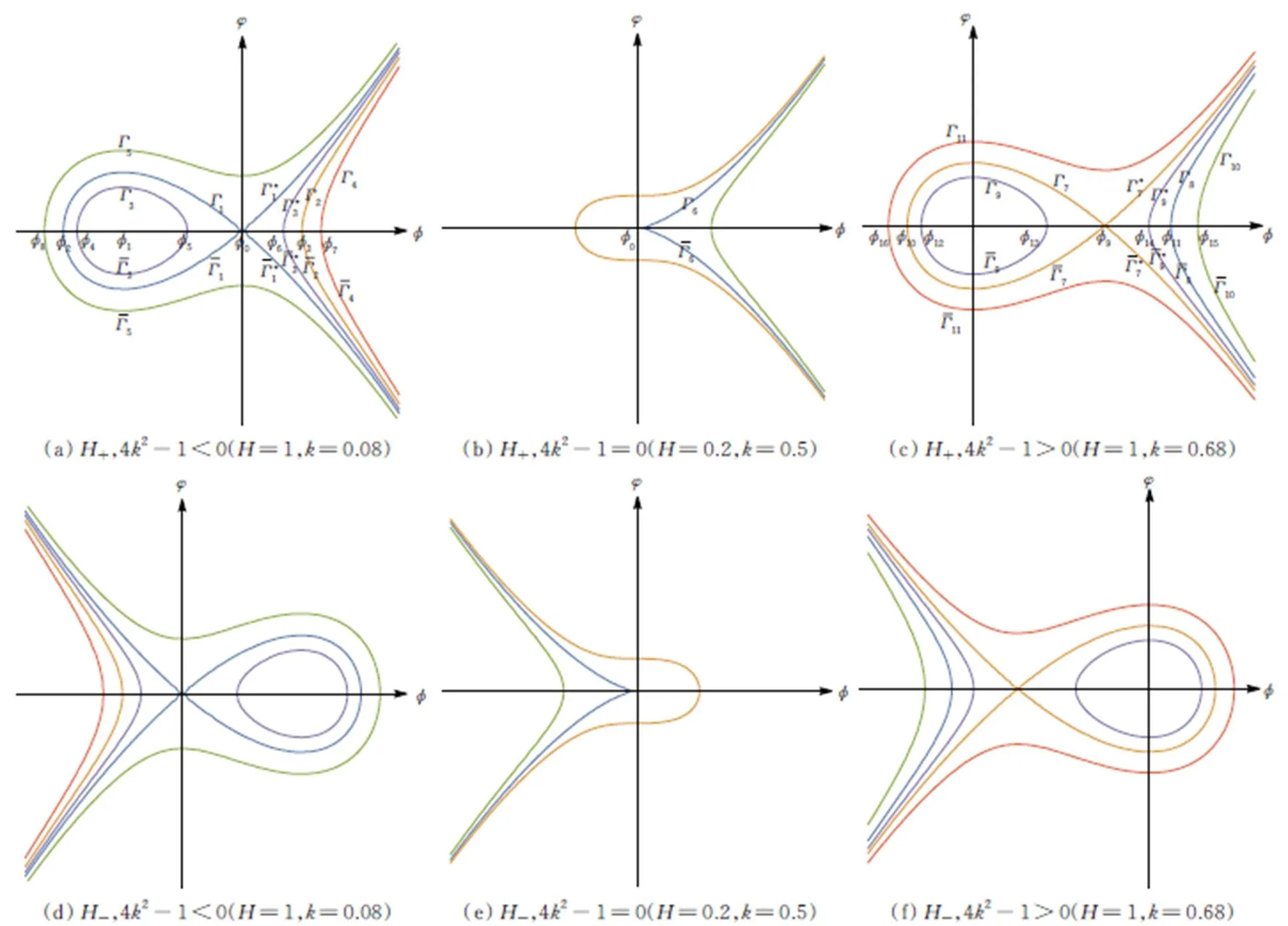
图1　在不同参数下式（9）的相图

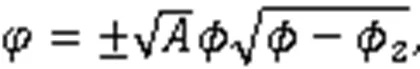
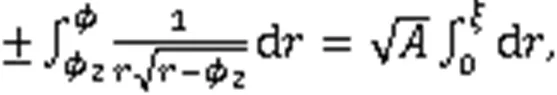
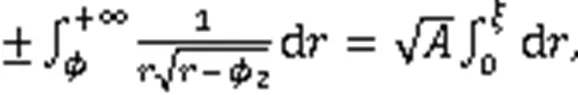
由式（3），得到2个孤立波解：

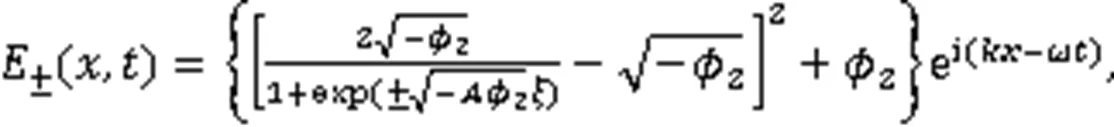
2个奇异波解：

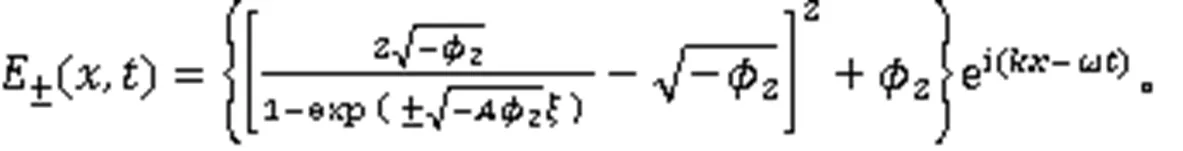
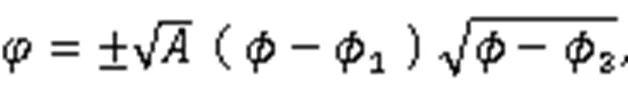
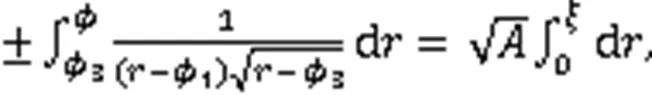
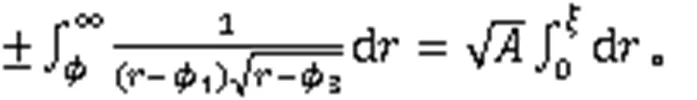
利用式（3），得到2个周期波解：

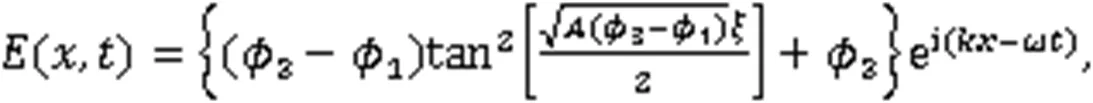
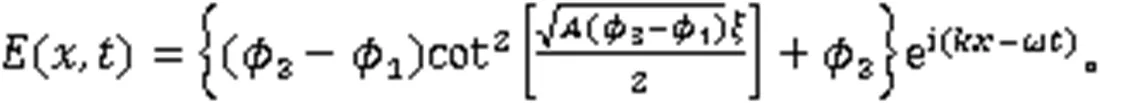
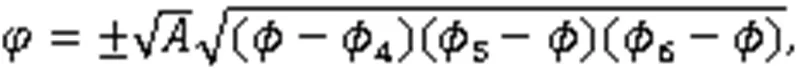
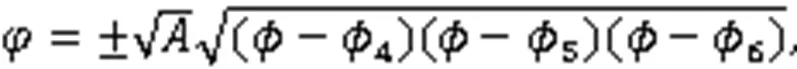
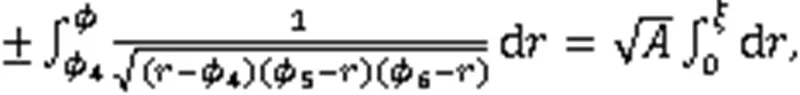
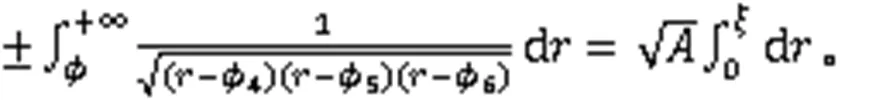
利用式（3），得到2个周期波解：

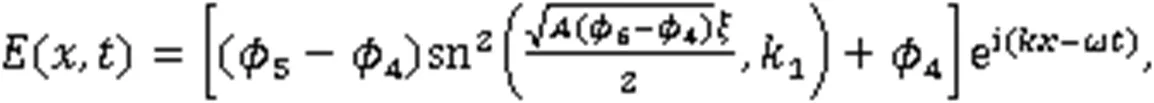
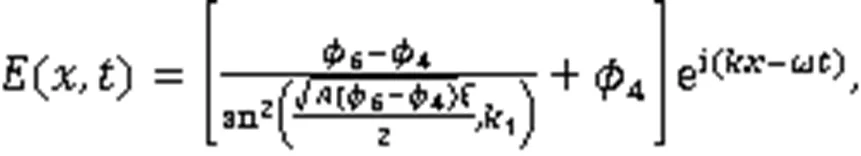
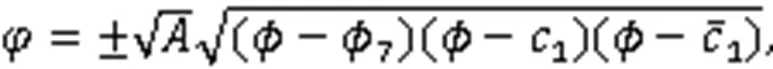
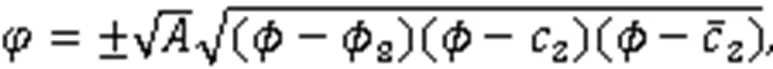
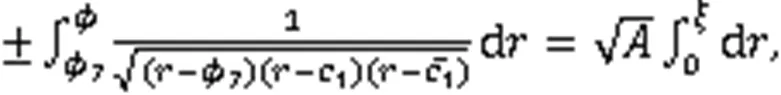
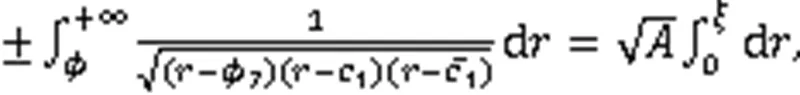
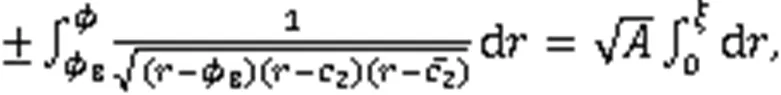
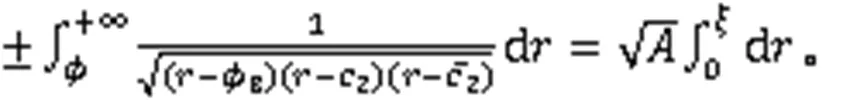
利用式（3），得到8个周期波解：

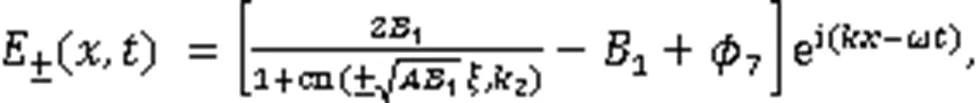
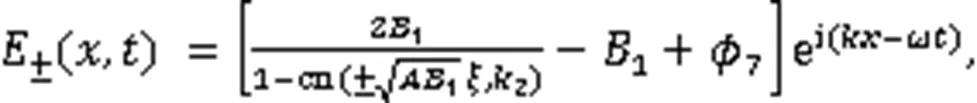
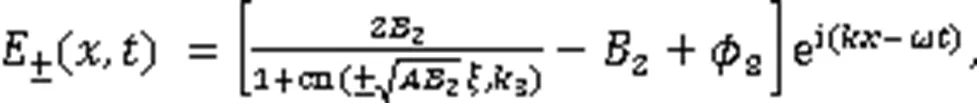
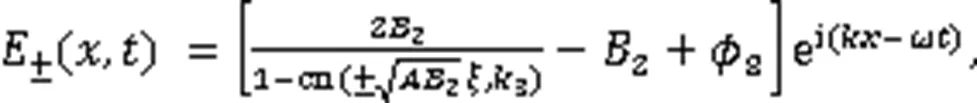
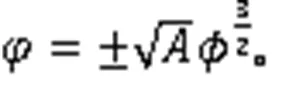
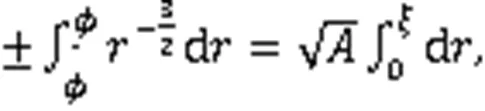
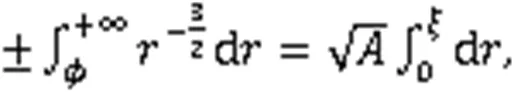
利用式（3），得到3个奇异波解：

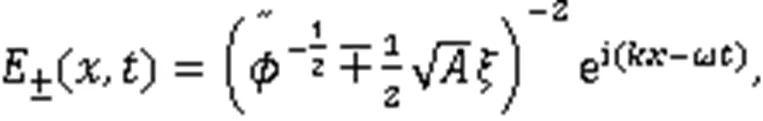
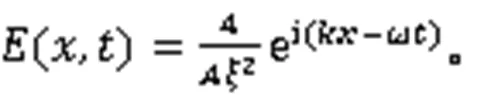
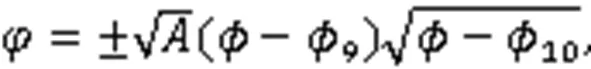
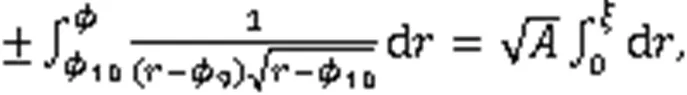
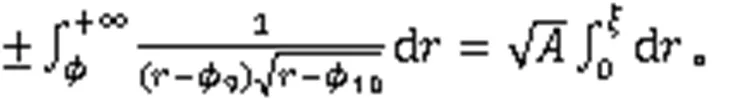
利用式（3），得到2个孤立波解：

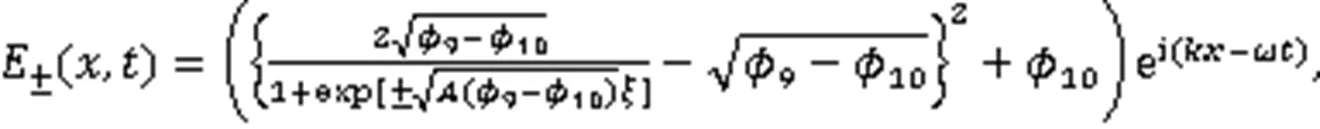
2个奇异波解：

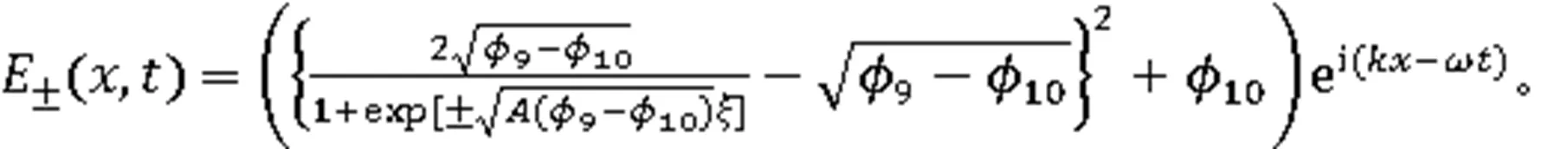
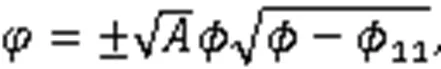
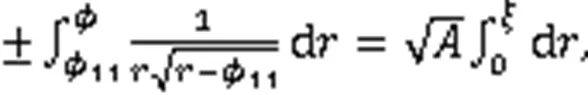
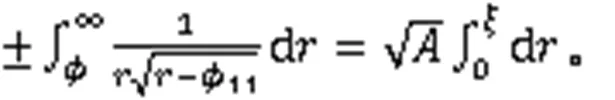
利用式（3），得到2个周期波解：

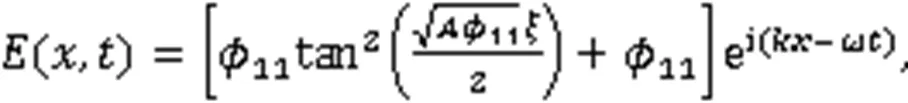
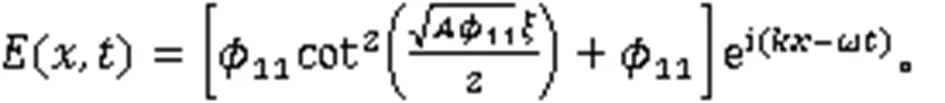
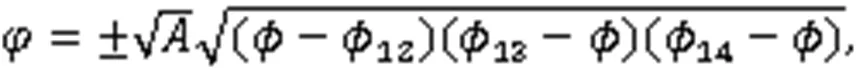
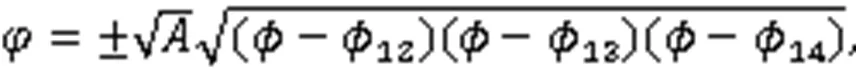
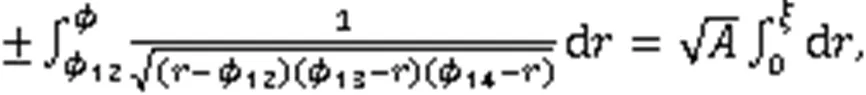
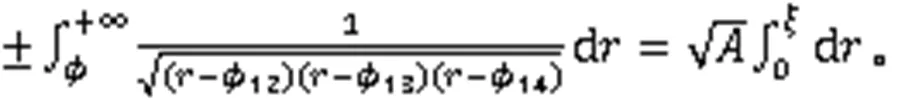
利用式（3），得到2个周期波解：

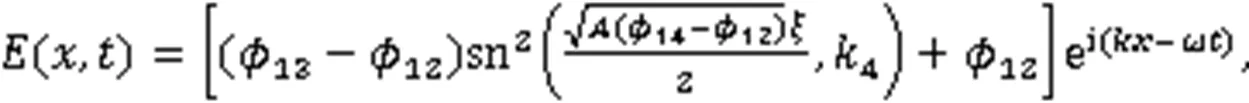
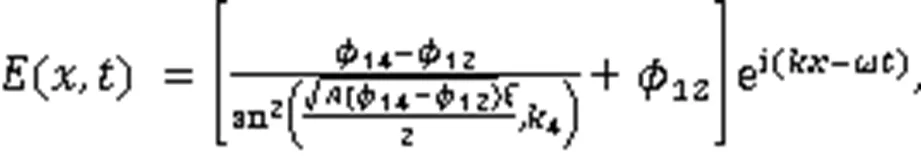
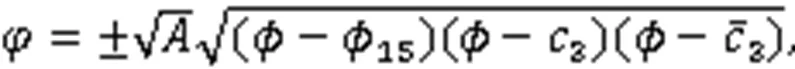
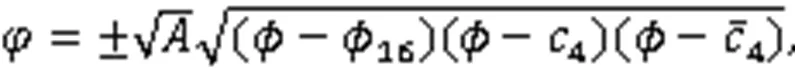
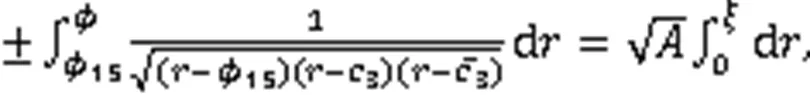
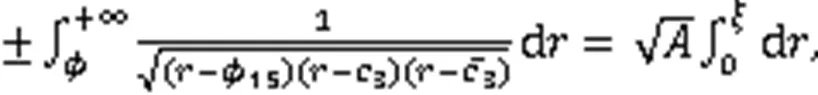
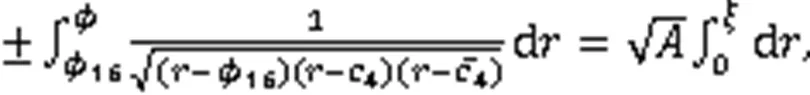
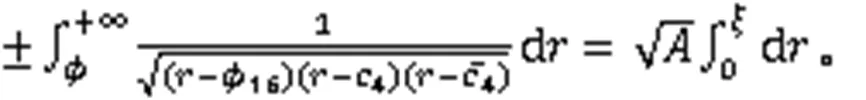
利用式（3），得到8个周期波解：

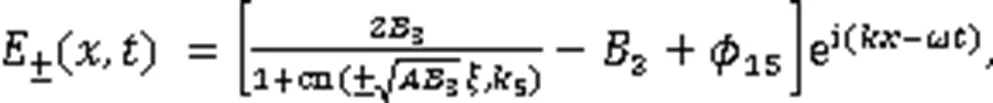
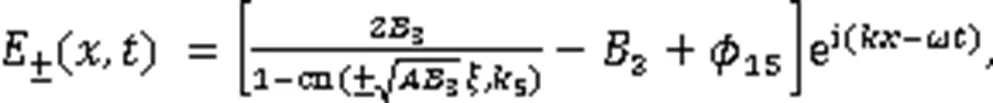
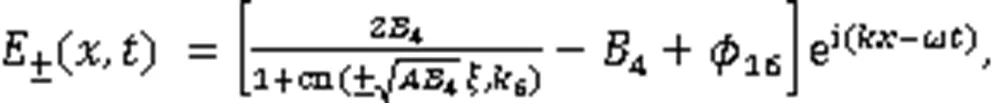
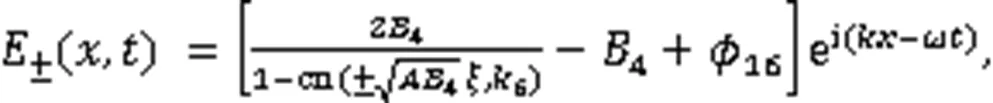
3　周期波解的演化过程

当参数取特殊值时，对周期波解取极限，得到相应的孤立波解和奇异波解。

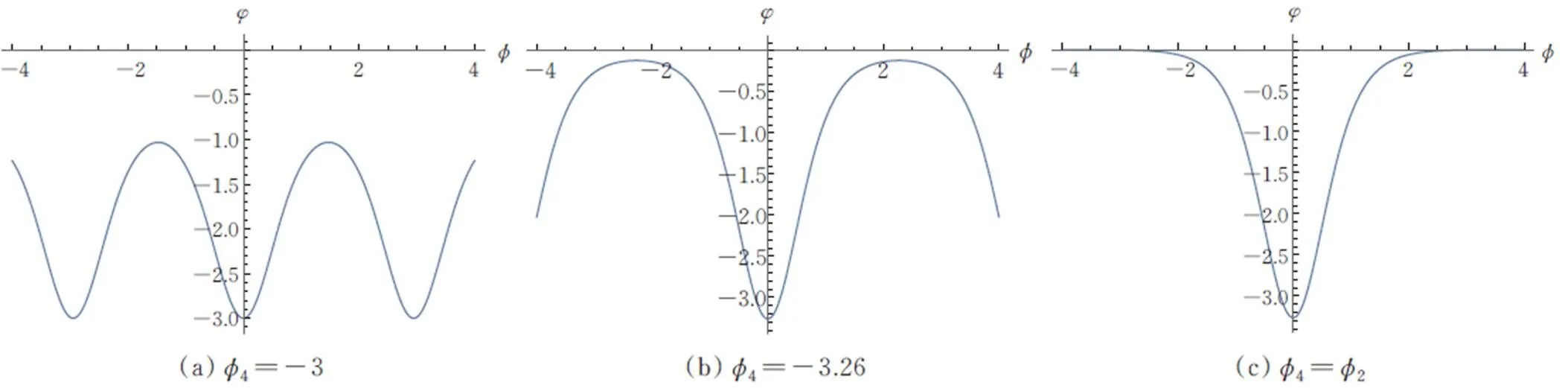
图2　当时，周期波解式（27）孤立波解式（16）

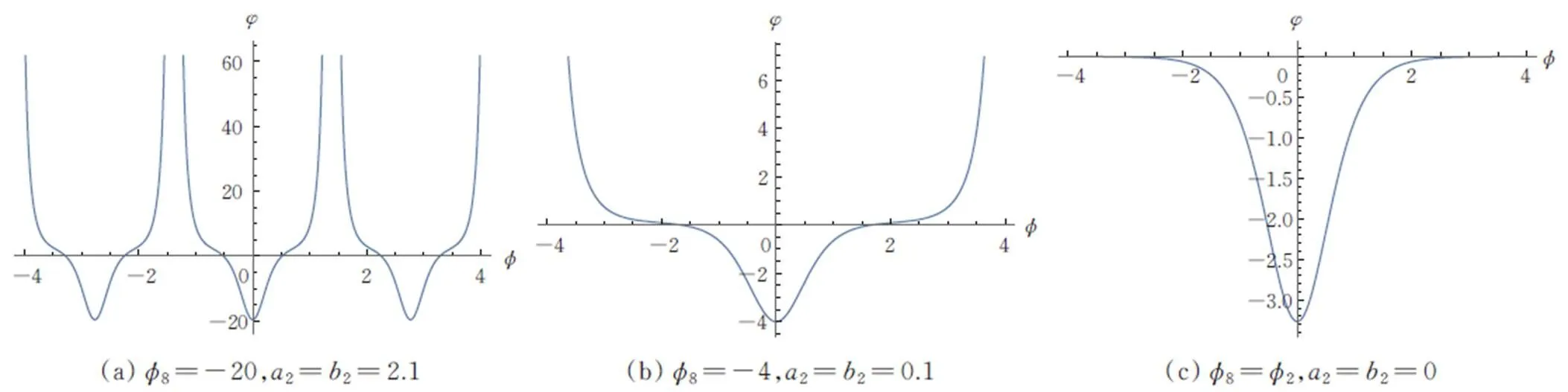
图3　当时，周期波解式（37）孤立波解式（16）

图4　当时，周期波解式（28）奇异波解式（17）

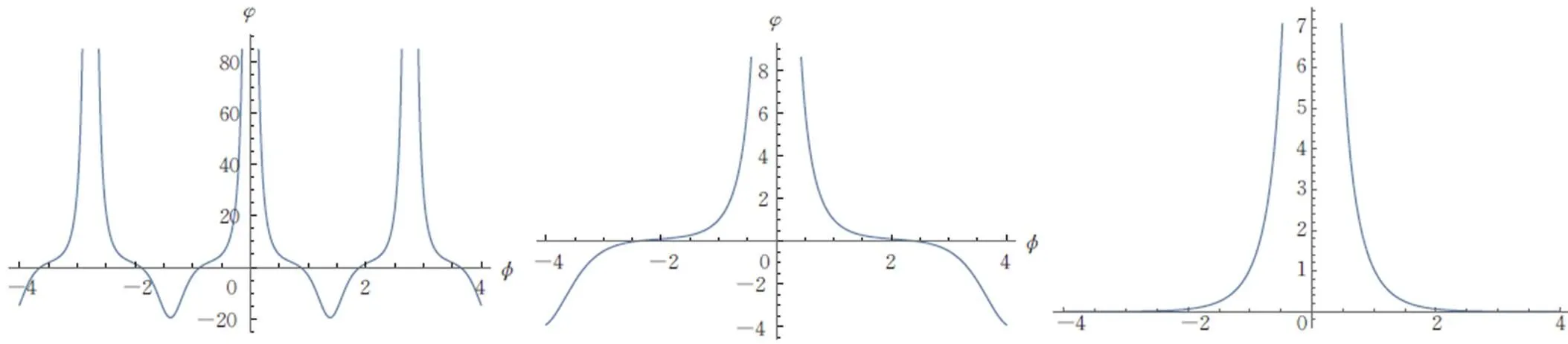
图5　当时，周期波解式（38）奇异波解式（17）

4　结论

［1］ ZAKHAROV V E. Collapse of Langmuir waves［J］. Soviet Physics JETP， 1972， 35（5）： 908-914.

［2］ GARCIA L G， HAAS F， OLIVEIRA L P L， et al. Modified Zakharov equations for plasmas with a quantum correction［J］. Physics of Plasmas， 2005， 12（1）： 3842. DOI：10.1063/1.1819935

［3］ 游淑军，郭柏灵，宁效琦. Langmuir扰动方程和Zakharov方程：光滑性与近似［J］. 应用数学和力学， 2012， 33（8）： 1013-1022. DOI：10.3879/j.issn.1000-0887.2012.08.009

YOU S J， GUO B L， NING X Q. Equations of Langmuir turbulence and Zakharov equations： Smoothness and approximation［J］. Applied Mathematics and Mechanics， 2012， 33（8）： 1013-1022. DOI：10.3879/j.issn.1000-0887.2012.08.009

［4］ LI L， FANG S M. The initial boundary value problem for modified Zakharov system［J］. Advances in Pure Mathematics， 2015， 5（5）： 278-285. DOI：10.4236/apm.2015.55028

［5］ YANG Q， DAI C Q， WANG Y Y， et al. Quantum soliton solutions of quantum Zakharov equations for plasmas［J］. Journal of the Physical Society of Japan， 2005， 74（9）： 2492-2495. DOI：10.1143/JPSJ.74.2492

［6］ 王悦悦，杨琴，戴朝卿，等. 考虑量子效应的Zakharov方程组的孤波解［J］. 物理学报， 2006， 55（3）： 1029-1034. DOI：10.3321/j.issn：1000-3290.2006.03.006

WANG Y Y， YANG Q， DAI C Q， et al. Solitary wave solution of Zakharov equation with quantum effect［J］. Acta Physica Sinica， 2006， 55（3）： 1029-1034. DOI：10.3321/j.issn：1000-3290.2006.03.006

［7］ ZHENG X X， SHANG Y D， DI H F. The time-periodic solutions to the modified Zakharov equations with a quantum correction［J］. Mediterranean Journal of Mathematics， 2017， 14（4）： 152. DOI：10.1007/s00009-017-0952-4

［8］ FANG S M， GUO C H， GUO B L. Exact traveling wave solutions of modified Zakharov equations for plasmas with a quantum correction［J］. Acta Mathematica Scientia， 2012， 32（3）： 1073-1082. DOI：10.1016/s0252-9602（12）60080-0

［9］ HAN L J，KONG Y，XIN L， et al. Exact periodic wave solutions for the modified Zakharov equations with a quantum correction［J］. Applied Mathematics Letters， 2019， 94： 140-148. DOI：10.1016/j.aml. 2019.01.009

［10］LI J B， LIU Z R. Smooth and non-smooth traveling waves in a nonlinearly dispersive equation［J］. Applied Mathematical Modelling， 2000， 25（1）： 41-56. DOI：10.1016/s0307-904x（00）00031-7

［11］LIU Z R， YANG C X. The application of bifurcation method to a higher-order KDV equation［J］. Journal of Mathematical Analysis and Applications， 2002， 275（1）： 1-12. DOI：10.1016/s0022-247x（02）00210-x

［12］SONG M， LIU Z R， ZERRAD E， et al. Singular soliton solution and bifurcation analysis of Klein-Gordon equation with power law nonlinearity［J］. Frontiers of Mathematics in China， 2013， 8（1）： 191-201. DOI：10.1007/S11464-012-0252-Z

［13］SONG M， LIU Z R. Periodic wave solutions and their limits for the ZK-BBM equation［J］. Applied Mathematics and Computation， 2014， 232（1）： 9-26. DOI：10.1016/j.amc.2014.01.048

［14］SONG M， LIU Z R， YANG C X. Periodic wave solutions and their limits for the modified KDV-KP equations［J］. Acta Mathematica Sinica （English Series）， 2015， 31（6）： 1043-1056. DOI：10.1007/s10114-015-3362-1

［15］WEN Z S. The generalized bifurcation method for deriving exact solutions of nonlinear space-time fractional partial differential equations［J］. Applied Mathematics and Computation， 2020， 366（1）： 124735. DOI：10.1016/j.amc.2019.124735

［16］SONG M， WANG B D， CAO J. Bifurcation analysis and exact traveling wave solutions for （2+1）-dimensional generalized modified dispersive water wave equation［J］. Chinese Physics B， 2020， 29（10）： 100206. DOI：10.1088/1674-1056/ab9f27

［17］SHI L J， WEN Z S. Bifurcations and dynamics of traveling wave solutions to a Fujimoto-Watanabe equation［J］. Communications in Theoretical Physics， 2018， 69（6）： 631-636. DOI：10.1088/0253-6102/69/6/631

［18］LIU Q S， ZHANG Z Y， ZHANG R G， et al. Dynamical analysis and exact solutions of a new （2+1）-dimensional generalized Boussinesq model equation for nonlinear Rossby waves［J］. Communications in Theoretical Physics， 2019， 71（9）： 1054-1062. DOI：10.1088/0253-6102/71/9/1054

［19］LI J B， CHEN G R， ZHOU Y. Bifurcations and exact traveling wave solutions of two shallow water two-component systems［J］. International Journal of Bifurcation and Chaos， 2021， 31（1）： 2150001. DOI：10.1142/S0218127421500012

［20］LIANG J L， LI J B， ZHANG Y. Bifurcations and exact solutions of an asymptotic Rotation-Camassa-Holm equation［J］. Nonlinear Dynamics， 2020， 101（4）： 2423-2439. DOI：10.1007/s11071-020-05868-0

Exact nonlinear wave solutions for the modified Zakharov equation with a quantum correction

WU Shenhui, SONG Ming

（，，312000，，）

bifurcation method; the modified Zakharov equation; nonlinear wave solutions

O 175.29

A

1008⁃9497（2023）01⁃030⁃08

2021⁃09⁃23.

国家自然科学基金资助项目（11775146）.

吴沈辉（1997—），ORCID：https：//orcid.org/0000-0002-8633-0769，男，硕士研究生，主要从事微分方程非线性波解研究，E-mail：wsh56314@163.com.

通信作者，ORCID：https：//orcid.org/0000-0003-4176-4923，E-mail：songming12_15@163.com.