一类二阶非齐次边值问题正解的存在性与多解性

石轩荣

一类二阶非齐次边值问题正解的存在性与多解性

石轩荣

（西北师范大学 数学与统计学院,甘肃 兰州 730070）

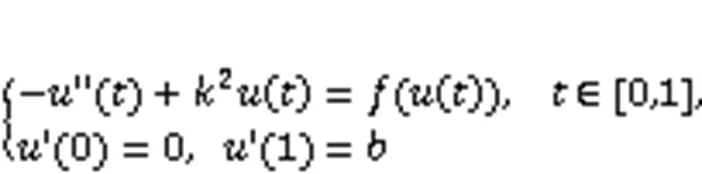
正解；多解性；上下解方法；拓扑度理论

0　引言

Neumann边值问题在数学物理中有重要应用，如平衡梁问题、流体流向问题、热传导问题等，因此备受关注，并在特定条件下验证了其解的存在性［1-7］。JIANG等［8］研究了二阶Neumann边值问题：

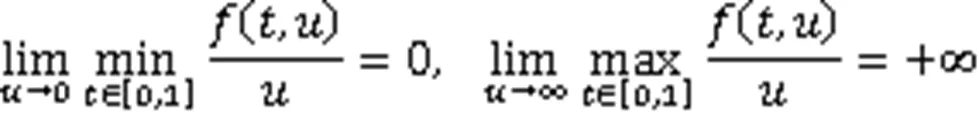
或

SUN等［9］研究了二阶Neumann边值问题

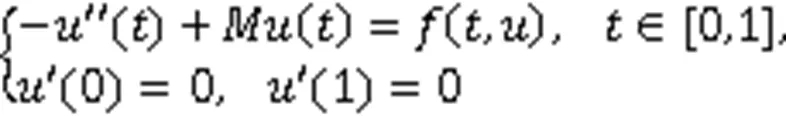
值得注意的是，文献［8-9］研究了齐次边界条件下二阶Neumann边值问题正解的存在性。涉及非齐次边界条件下二阶微分方程边值问题的研究较少，当二阶Neumann边值问题的边界条件为非齐次时是否存在正解？本文将给出一个肯定的回答。

1　预备知识

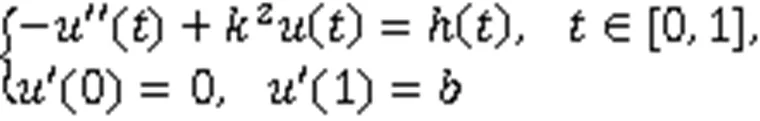
有唯一解：

其中，

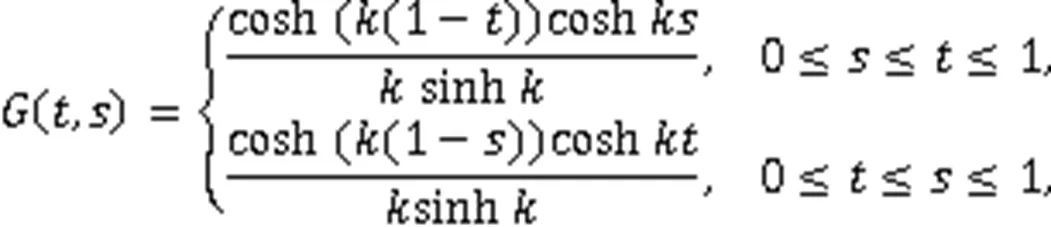
证明由文献［8-9］，易得

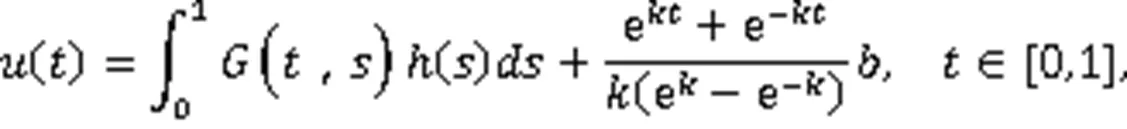
定义

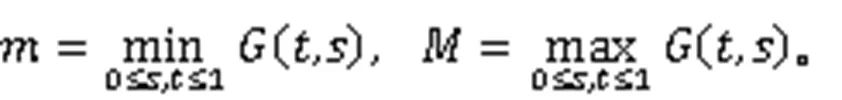
有唯一解：

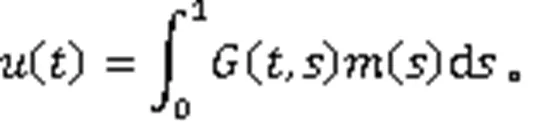
证明由引理1易证。

2　主要结果及其证明

假设：

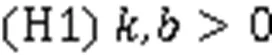
考察问题

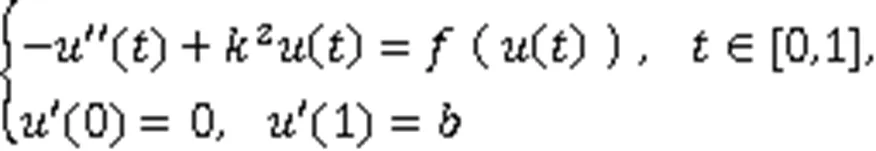
正解的存在性与多解性，则有以下主要结果。

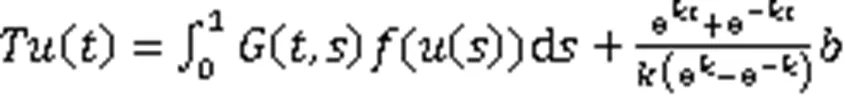
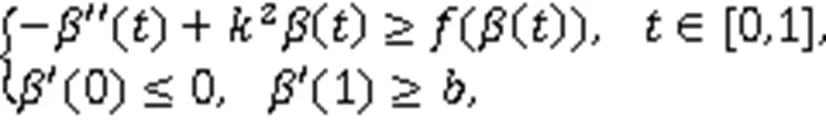
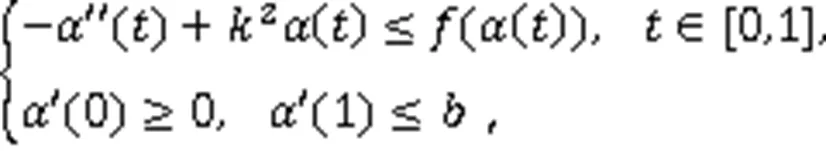
证明考察辅助问题：

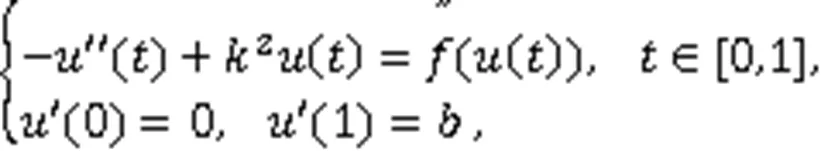
定义

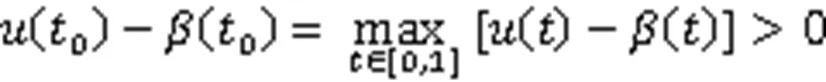
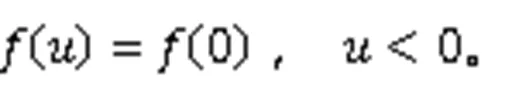
定理2的证明主要分为4步。

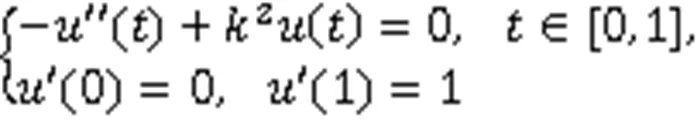
的解，易得

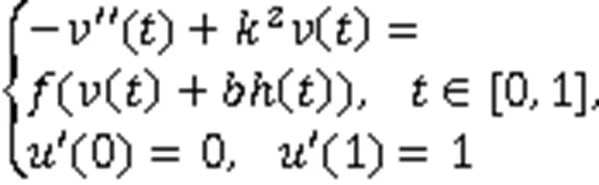
的正解。

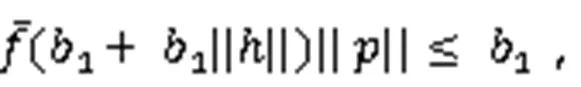
的唯一解。

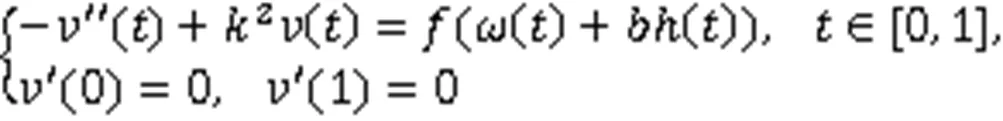
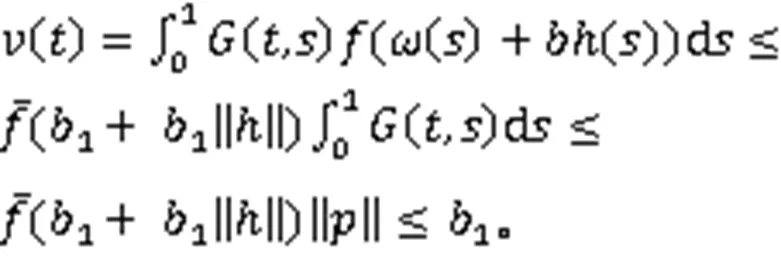
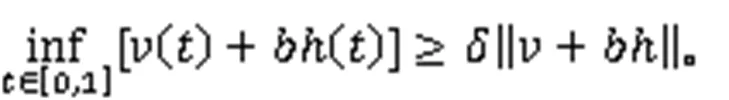
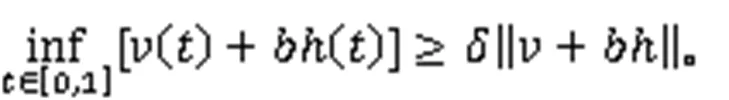
可得

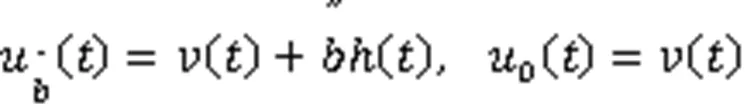
定义

令

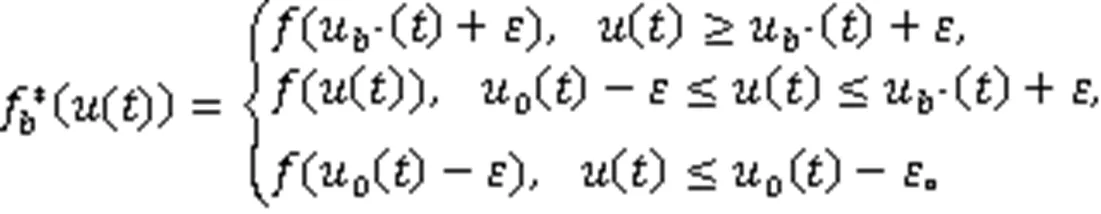
令

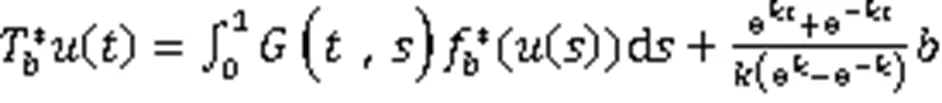
所以

且

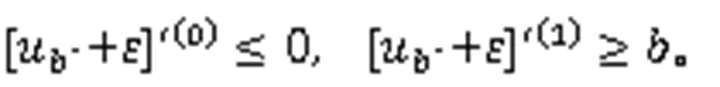
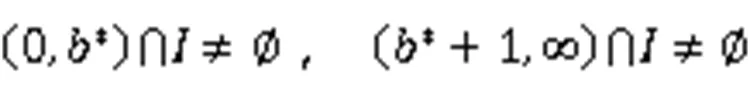
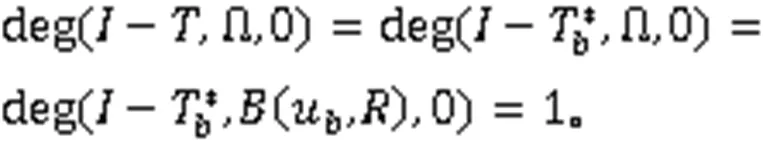
此外，由于式（5）的所有解有界，所以

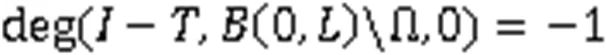
［1］ TARIBOON J， SITTHIWIRATTHAM T. Positive solutions of a nonlinear three-point integral boundary value problem［J］. Boundary Value Problems， 2010， 24（5）： 1-11. DOI：10.1155/2010/519210

［2］ CHU J F， SUN Y G， CHEN H. Positive solutions of Neumann problems with singularities［J］. Journal of Mathematical Analysis and Applications， 2008， 337（2）： 1267-1272. DOI：10.1016/j.jmaa.2007.04.070

［3］ WANG H Z， LI Y. Neumann boundary value problems for second-order ordinary differential equations across resonance［J］. SIAM Journal on Control and Optimization，1995， 33（5）： 1312-1325. DOI：10.1137/S036301299324532X

［4］ JIANG D Q， YANG Y， CHU J F， et al. The monotone method for Neumann functional differential equations with upper and lower solutions in the reverse order［J］. Nonlinear Analysis： Theory， Methods & Applications， 2007， 67（10）： 2815-2828. DOI：10. 1016/j.na.2006.09.042

［5］ MA R Y， GAO C H， CHEN R P. Existence of positive solutions of nonlinear second-order periodic boundary value problems［J］. Boundary Value Problems， 2010， 2012： 1-18. DOI：10.1155/2010/626054

［6］ WANG F， ZHANG F， WANG F L. The existence and multiplicity of positive solutions for second-order periodic boundary value problem［J］. Journal of Function Spaces and Applications， 2012， 2012： 1-13. DOI：10.1155/2012/725646

［7］ ZHANG Z X， WANG J Y. On existence and multiplicity of positive solutions to periodic boundary value problems for singular nonlinear second order differential equations［J］. Journal of Mathematical Analysis and Applications， 2003， 281（1）： 99-107. DOI：10.1016/S0022-247X（02）00538-3

［8］ JIANG D Q， LIU H Z. Existence of positive solutions to second-order Neumann boundary value problem［J］. Journal of Mathematical Research and Exposition， 2000， 20（3）： 360-364.

［9］ SUN J P， LI W T. Multiple positive solutions to second-order Neumann boundary value problems［J］. Applied Mathematics and Computation， 2003， 146（1）： 187-194. DOI：10.1016/S0096-3003（02）00535-0

［10］MA R Y. Existence of positive radial solutions for elliptic systems［J］. Journal of Mathematical Analysis and Applications， 1996， 201（2）： 375-386. DOI：10.1006/jmaa.1996.0261

［11］ERBE L H， WANG H Y. On the existence of positive solutions of ordinary differential equations［J］. Proceedings of the American Mathematical Society，1994， 120（3）： 743-748. DOI：10.2307/2160465

［12］JIANG D Q， CHU J F， ZHANG M R. Multiplicity of positive periodic solutions to superlinear repulsive singular equations［J］. Journal of Differential Equations， 2005， 211（2）： 282-302. DOI：10.1016/j.jde.2004.10.031

Existence and multiplicity of positive solutions for a class of second-order nonhomogeneous boundary value problems

SHI Xuanrong

（，，730070，）

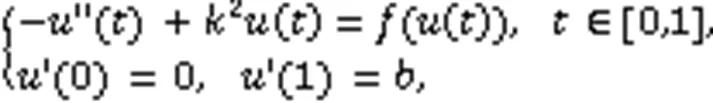
positive solutions; multiplicity; upper and lower solutions; topological degree theory

O 175.8

A

1008⁃9497（2023）01⁃038⁃05

2022⁃01⁃08.

国家自然科学基金资助项目（12061064）.

石轩荣（1998—），ORCID：https：//orcid.org/0000-0002-7496-6348，男，硕士研究生，主要从事常微分方程与动力系统研究，E-mail： SXR15209336785@163.com.