基于DE-ELM算法的配电网电力系统负荷预测研究
洪 宇 , 高 骞, 杨俊义, 梁永青
(1. 国网江苏省电力有限公司 连云港供电分公司, 江苏 连云港 222000;2. 国网江苏省电力有限公司, 南京 210024; 3. 北京国电通网络技术有限公司, 北京 100085)
0 引 言
配电网电力系统负荷预测作为保障电力系统安全运行、 维护配电网的输电质量、 实现持续供电的重要手段之一, 在电力运行中起到巨大的作用[1]。随着智能电网的快速发展, 如何制定科学决策, 高效地对配电网进行电力负荷精度的预测, 成为当今电力系统急需解决的问题[2]。
陈先飞等[3]提出基于MGM(1,n,r)的主动配电网中长期负荷预测。该方法首先对配电网电力系统增长负荷影响因素进行分析, 依据分析结果确定相关模型参数; 再依据灰度预测方法建立配电网的多变量灰色负荷预测模型; 最后通过该模型计算电力系统的最优参数解, 实现电力系统的负荷预测。该方法由于未能在电力负荷预测前, 对电力数据进行缺失值插补处理, 导致该方法电力负荷的预测精度低。李颖等[4]提出自下而上的主动配电网负荷曲线化预测方法。该方法通过对预测区域用电量性质的分析, 将预测区域分割成若干小区域块, 并利用分类算法对其进行分类处理; 再通过处理结果建立负荷曲线调控模型, 制定相关管理策略; 最后通过模型计算小区域块电力负荷, 根据制定的管理策略整合电力负荷结果, 实现对配电网电力负荷的预测。该方法在进行区域分割时存在一些不足, 预测性能较差。赵凤展等[5]提出基于变分模态分解-BA-LSSVM(Bat Algorithm-Least Squares Support Vector Machine)算法的配电网短期负荷预测。该方法通过模态分解法将电力系统原始负荷序列分解成不同频率的子序列; 依据支持向量机建立电力系统负荷预测模型; 最后将分解的子序列放入模型中进行求解, 根据求解结果实现电力系统负荷的短期预测。该方法在建立负荷预测模型时存在偏差, 导致其预测时间长。
为解决上述电力系统负荷预测过程中出现的问题, 笔者提出一种基于DE-ELM(Differential Evolution-Extreme Learning Machine)算法的配电网电力系统负荷预测研究方法。
1 配电网电力系统数据预处理
在对配电网电力系统进行负荷预测前, 需要利用相关方法对电力系统数据进行处理。
1.1 配电网电力系统数据去噪
在对配电网电力系统数据进行采集时, 会将杂乱的电力噪声数据一并采集, 从而影响电力系统负荷的预测精度。因此对配电网电力系统进行去噪处理, 是电力负荷预测的重要流程之一[6]。
电力数据的噪声信号为g(x), 小波变换流程如下

(1)
其中Sβz(c,p)为电力数据噪声信号的小波变换结果,c为信号的尺度因子,p为平移因子,Sβz(c,p)为共轭函数, dt为信号尺度。
基于上述变换过程, 建立噪声信号的小波变换条件, 以此还原噪声信号, 结果如下

(2)
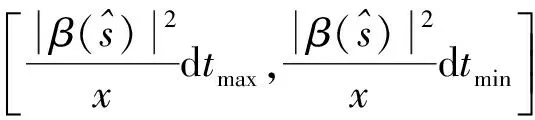

(3)
其中I2(E)为变换结果,j和k分别为常数。最后依据变换结果完成电力系统数据的去噪处理。
1.2 电力系统数据缺失值插补
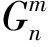
1) 设定网络时间片滤波为εn(i), 对电力系统数据的当前隐藏状态进行估计, 并初始化网络结构的各项参数值, 过程如下

(4)

2) 依据上述计算结果, 对网络数据先验概率、 条件概率以及数据状态信息进行迭代计算, 获取贝叶斯网络在时间片n时的数据隐变量状态转移概率Yn-1。
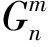
4) 依据上述流程依次对不同时间片状态转移概率进行计算, 寻找其中缺失数据。若网络时间片中存在缺失数据, 基于上述流程完成电力数据的缺失值插补, 若无缺失数据, 转入流程6)。
5) 对式(4)进行计算, 利用计算结果获取概率分布函数集, 实现缺失数据的插补, 过程如下

(5)
其中β(Yn+1,Gn+1)为电力缺失值插补结果。
6) 辨别时间片是否迭代完成, 停止计算。
具体数据插补流程如图1所示。

图1 电力缺失数据插补流程图Fig.1 Flow chart of interpolation of missing power data
2 配电网电力系统负荷预测
依据上述获取的完整电力系统数据, 基于DE-ELM算法实现配电网的电力系统负荷预测。
2.1 算法描述
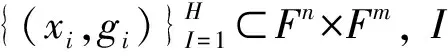
首先, 在隐藏层中随机选定一组神经元参数(ci,di),c为数据的输入权重,d为阈值, 建立隐藏层的输出矩阵, 获取电力负荷输出函数值, 过程如下
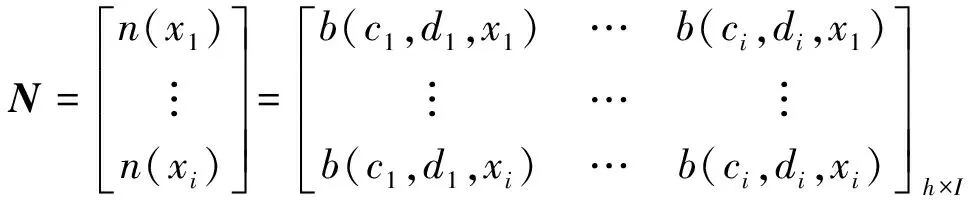
(6)
其中N为隐藏层输出矩阵,b(ci,di,xi)为电力负荷输出函数。基于获取的电力输出函数, 计算隐藏层与输出层之间的权值, 过程如下
δ=N+H
(7)
其中H为电力系统数据样本的实际输出,N+为伪逆矩阵。最后依据上述计算结果, 完成电力负荷的输出预测, 并由相关阈值辨别预测精度, 过程如下

(8)
其中Sj为电力负荷[9]的预测值,Gj为实际负荷值, |Sj-Gj|为绝对误差,A(c,d)为实际误差值,θ为常数。
2.2 算法改进
由于传统ELM算法在进行电力负荷预测时, 预测误差较大, 所以将全局寻优法(DE: Differential Evolution)引入ELM算法中对算法进行优化。依据蚁群算法对ELM算法中的输入权重c, 阈值d进行寻优搜索, 基于最小化的预测误差, 获取电力负荷的最佳期望网络模型。从而实现电力负荷的高精度预测。
全局寻优方法[10]是通过对种群的初始化, 对随机个体的预测差值进行加权处理生成新的群体, 随机挑选新个体进行交叉、 变异操作获取新的个体值, 最后通过适应度函数值的计算, 确定将其保留或剔除。过程如下。
1) 初始化群体。设定蚁群群体为Q, 维度为W, 迭代次数为T, 群体变异因子为B, 区间为[0,2]; 交叉因子为C, 在[0,1]之间,t为当前时刻迭代次数, 种群个体描述过程如下

(9)
其中Si,0为种群的初始形式,Si,t为种群个体,E为种群数量,i为常数。
2) 评价种群个体值。建立相应的适应度函数f(Si,t), 对种群中个体的适应度值进行计算。
3) 交叉、 变异操作。在种群中随机生成不同的新个体, 并对其进行交叉、 变异操作, 获取新的训练个体值Ji,t。
4) 选择。将进行变异操作的个体进行适应度值的对比, 保留适应度较大的个体值, 过程如下
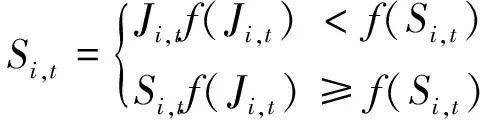
(10)
其中f为适应度函数。
5) 停止条件。依据迭代次数判断是否完成迭代, 基于终止条件则停止迭代, 完成输出, 获取电力负荷预测值。最后依据输出的电力负荷训练值, 实现配电网电力系统负荷预测。
2.3 预测流程
配电网电力系统具体负荷预测流程如下:
1) 基于配电网电力系统采集电力数据, 进行去噪、 缺失值插补处理, 获取完整电力数据集;
2) 将数据集划分成训练集、 测试集两部分;
3) 使用DE-ELM算法计算训练数据集, 建立网络模型, 再将测试集放入模型中进行迭代训练, 依据模型输出结果实现配电网电力系统负荷预测。
3 实 验
为验证上述配电网电力系统负荷预测方法的整体有效性, 需要对此方法进行测试。
3.1 实验结果及分析
分别采用基于DE-ELM算法的配电网电力系统负荷预测研究、 基于MGM(1,n,r)的主动配电网中长期负荷预测[3]、 基于变分模态分解-BA-LSSVM算法的配电网短期负荷预测[5]进行测试。
在进行配电网电力系统负荷预测过程中, 适应度值的高低、 预测误差的大小都会影响预测效果。采用上述所提方法, 对3种预测影响指标进行测试, 从而检测3种方法的预测性能。
1) 预测精度测试。预测误差的高低对预测效果的影响巨大。设定均方根误差RMSE(Root Mean Square Error)和最大相对误差max_Error为电力负荷预测误差指标, 计算过程如下

(11)
其中h为电力数据样本数量,x′为预测电力负荷值,xi为实际负荷值。基于上述预测误差指标, 测试3种负荷预测方法的预测精度, 测试结果如图2所示。
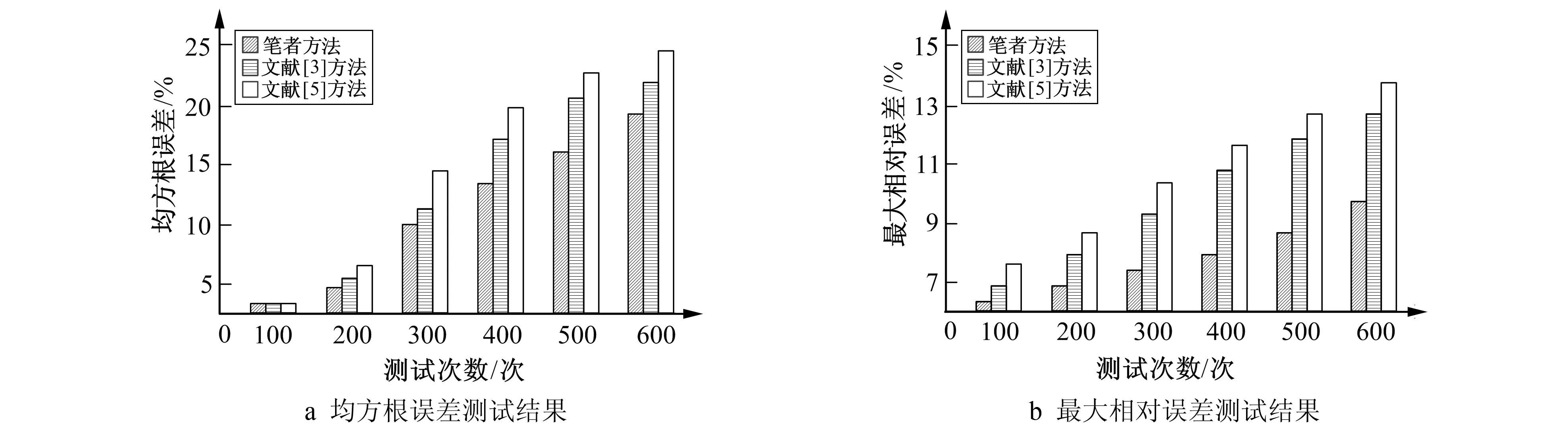
图2 不同电力负荷预测方法的预测精度测试结果Fig.2 Forecast accuracy of different power load forecasting methods

图3 不同预测方法的预测时间测试结果Fig.3 The prediction time of different prediction methods
分析图2可知, 测试次数的不同, 检测出的预测误差也不相同。笔者方法不管是均方根误差的测试还是最大相对误差的测试, 检测结果都低于其他两种电力负荷预测方法。这主要是因为笔者方法在进行电力负荷预测时, 对电力数据进行了缺失值插补, 所以笔者方法在预测电力负荷时的预测精度高。
2) 预测时间测试。基于上述测试结果, 测试笔者、 文献[3]以及文献[5]方法电力负荷预测时间, 测试结果如图3所示。
电力负荷预测次数的不同, 测试出的电力负荷预测时间也不相同。分析图3可知, 笔者方法测试得出的电力负荷预测时间少于文献[3]和文献[5]方法测试结果。这主要是因为笔者方法在进行电力负荷检测前, 对电力负荷数据缺失值进行了插补处理, 所以笔者方法在进行电力负荷预测时的预测时间短。由此可佐证笔者方法的预测性能好。
4 结 语
配电网技术的不断更新, 使传统的电力负荷预测方法无法有效的完成电力的负荷预测任务, 针对其中出现的问题, 笔者提出了基于DE-ELM算法的配电网电力系统负荷预测研究方法。该方法首先对电力数据进行预处理, 并基于处理结果插补电力缺失值; 再依据DE-ELM算法对电力数据进行计算, 从而实现对配电网电力系统的负荷预测。
参考文献:
[1]林君豪, 张焰, 赵腾, 等. 基于改进卷积神经网络拓扑特征挖掘的配电网结构坚强性评估方法 [J]. 中国电机工程学报, 2019, 39(1): 84-96,323.
LIN Junhao, ZHANG Yan, ZHAO Teng, et al. Structure Strength Assessment Method of Distribution Network Based on Improved Convolution Neural Network and Network Topology Feature Mining [J]. Proceedings of the CSEE, 2019, 39(1): 84-96,323.
[2]张莉, 高岩, 朱红波, 等. 考虑用电量不确定性的智能电网实时定价策略 [J]. 电网技术, 2019, 43(10): 3622-3631.
ZHANG Li, GAO Yan, ZHU Hongbo, et al. Real-Time Pricing Strategy Based on Uncertainty of Power Consumption in Smart Grid [J]. Power System Technology, 2019, 43(10): 3622-3631.
[3]陈先飞, 何山, 王杰, 等. 基于MGM(1,n,r)的主动配电网中长期负荷预测 [J]. 太阳能学报, 2020, 41(2): 188-193.
CHEN Xianfei, HE Shan, WANG Jie, et al. Mid-Long Term Load Forecasting of Active Distribution Network Based on MGM(1,n,r) [J]. Acta Energiae Solaris Sinica, 2020, 41(2): 188-193.
[4]李颖, 张跃, 吴琳, 等. 自下而上的主动配电网负荷曲线化预测方法 [J]. 电力系统及其自动化学报, 2019, 31(2): 106-111.
LI Ying, ZHANG Yue, WU Lin, et al. Bottom-Up Active Distribution Network Load Curve Forecasting Method [J]. Proceedings of the CSU-EPSA, 2019, 31(2): 106-111.
[5]赵凤展, 郝帅, 张宇, 等. 基于变分模态分解-BA-LSSVM算法的配电网短期负荷预测 [J]. 农业工程学报, 2019, 35(14): 190-197.
ZHAO Fengzhan, HAO Shuai, ZHANG Yu, et al. Short-Term Load Forecasting of Distribution Network Based on Variational Modal Decomposition-BA-LSSVM Algorithm [J]. Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(14): 190-197.
[6]屈星, 李欣然. 考虑配电网结构的电力系统综合负荷建模 [J]. 电力系统自动化, 2020, 44(12): 117-123.
QU Xing, LI Xinran. Synthesis Load Modeling of Power System Considering Distribution Network Structure [J]. Automation of Electric Power Systems, 2020, 44(12): 117-123.
[7]杨柳依, 马社祥, 孟鑫. 基于双树复小波变换的单通道盲源分离算法 [J]. 计算机仿真, 2019, 36(10): 248-252,264.
YANG Liuyi, MA Shexiang, MENG Xin. Single-Channel Blind Source Separation Based on Dual-Tree Complex Wavelet Decomposition [J]. Computer Simulation, 2019, 36(10): 248-252,264.
[8]骆小满, 阮江军, 邓永清, 等. 基于多物理场计算和模糊神经网络算法的变压器热点温度反演 [J]. 高电压技术, 2020, 46(3): 860-866.
LUO Xiaoman, RUAN Jiangjun, DENG Yongqing, et al. Transformer Hot-Spot Temperature Inversion Based on Multi-Physics Calculation and Fuzzy Neural Network Algorithm [J]. High Voltage Engineering, 2020, 46(3): 860-866.
[9]张志, 杜延菱, 崔慧军, 等. 考虑关联因素的智能化中长期电力负荷预测方法 [J]. 电力系统保护与控制, 2019, 47(2): 24-30.
ZHANG Zhi, DU Yanling, CUI Huijun, et al. Intelligent Mid-Long Electricity Load Forecast Method Considering Associated Factors [J]. Power System Protection and Control, 2019, 47(2): 24-30.
[10]陈经伟, 刘新贵, 孙傲辉, 等. 全局寻优的点状地名自动匹配方法研究 [J]. 测绘科学技术学报, 2020, 37(5): 525-530.
CHEN Jingwei, LIU Xingui, SUN Aohui, et al. Research on Automatic Matching Method of Point-Like Toponyms Based on Global Optimization [J]. Journal of Geomatics Science and Technology, 2020, 37(5): 525-530.

