基于贝叶斯的核磁共振T2谱成像方法
王 琦, 杜海龙, 高 威, 刁 庶
(1. 吉林大学 通信工程学院, 长春 130012; 2. 无锡职业技术学院 控制技术学院, 江苏 无锡 214121)
0 引 言
核磁共振(NMR: Nuclear Magnetic Resonance)作为一种快速、 无损的探测技术, 被广泛应用于食品科学、 高分子材料和石油勘探等领域[1-3]。通常, 背景场强度大于0.5 T的情况为高场核磁共振, 低于0.5 T为低场核磁共振。相对于高场核磁共振, 低场核磁共振具有成本低、 原位测试等优点。目前, 低场核磁共振主要是基于T2谱分析方法, 通常用于检测物质的物理性质[4-5]。因此,T2谱成像精度对提高检测结果的准确性十分重要。
近年来, 国内外针对NMR的T2谱成像进行了大量研究[6-7]。主要有非负最小二乘法、 罚函数法和非负奇异值分解法(SVD: Singular Value Decomposition) 等算法[8-9]。但通过上述方法得到的T2谱通常是连续分布的, 不适用于具有不光滑的T2值的样品。为此, 蒋川东等[10]提出了基于L1范数的T2谱成像方法, 实现了稀疏模型的高分辨率成像。但对不均匀分布随机的T2谱, 上述方法会导致部分细节丢失。
贝叶斯方法是其中一种概率性算法, 其采用马尔可夫链蒙特卡罗(MCMC: Markov Chain Monte Carlo)策略在先验空间进行采样, 该方法不仅可以量化成像的不确定度, 并且能统计预测模型的后验概率[11]。因此, 笔者研究了基于贝叶斯的核磁共振T2谱成像方法。
1 基于贝叶斯的核磁共振T2谱成像方法
1.1 低场核磁共振原理
低场核磁共振通过施加射频脉冲(CPMG: Carr-Purcell-Meiboom-Gill)序列, 激发介质中的氢质子1H 发生共振, 发射脉冲停止后1H释放能量,横向磁化矢量迅速衰减(横向磁化矢量衰减的时间即为横向弛豫时间T2), 此时通过接收线圈即可采集得到NMR回波曲线, 表示为

(1)
其中τ为半回波间隔时间,n为回波个数,Am和T2m分别为第m个弛豫分量的幅值和横向弛豫时间,M为弛豫分量个数。一一对应的Am和T2m即构成了样品的T2谱。
1.2 基于贝叶斯的核磁共振T2谱成像方法
由贝叶斯原理,T2谱成像的框架可表示为[12]

(2)
其中P(s|j)为似然函数,P(j)为横向弛豫时间T2的先验概率密度函数,P(s)为NMR观测回波数据的概率密度函数。P(j|s)则为待求的T2后验概率密度函数, 根据后验分布可获得T2成像结果的期望、 不确定度等统计信息[13]。
假设NMR观测回波数据的噪声服从高斯分布, 且与T2相互独立, 则NMR贝叶斯反演的似然函数可表示为一种多维正态分布
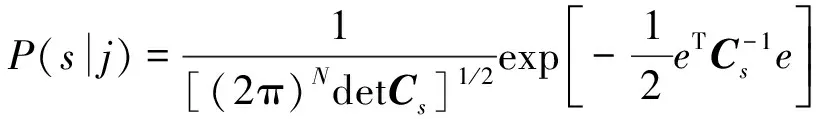
(3)
其中e为观测数据与迭代模型下的NMR正演响应下的差值;Cs为观测数据的协方差矩阵, detCs为其行列式。
适当的先验信息对于贝叶斯反演的准确性至关重要, 而弛豫时间T2符合多峰高斯分布, 表示为

(4)
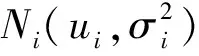
使用改进的Metropolis方法求解式(2), 即得到T2谱成像结果, 具体步骤如下。

2) 基于先验样本进行随机游走, 生成新的建议模型Tp, 计算其似然函数P(Tp)。
3) 判断新的建议模型是否取代当前模型。计算接受概率

(5)
判断是否接受新样本, 如果接受, 则马尔科夫链发生从模型Tc到Tp的状态转变。否则, 重新进行1)~3)[14-15]。进一步, 笔者结合序贯Gibbs采样策略, 在原模型变量的基础上进行随机扰动进而产生新的模型, 扰动“步长”设置成跟随迭代次数自适应减小。同时, 利用模拟退火方法调节马尔科夫链中建议模型的接受概率[16]。
2 实验结果及分析
为验证核磁共振贝叶斯成像方法的有效性, 笔者随机构造服从多峰的混合高斯概率密度函数的T2谱模型, 即以30%的概率服从N(8,82)、 以70%的概率服从N(2,12), 如图1中星花曲线所示。T2的布点数为40, 在10-3~10 s间呈等对数间隔分布。回波间隔2τ=5 ms, 回波数n=1 000, 利用式(1)计算得到NMR回波曲线, 并加入高斯噪声, 信噪比为40 dB, 如图2中虚线所示。利用改进的Metropolis方法, 对数据进行T2谱成像。假定先验模型假设为20%的概率服从N(8,82)、 以80%的概率服从N(2,22)。归一化最大值和最小值0.001和30, 并行运算4条Markov链, 每条链的采样次数为5万次, Markov链的初始状态随机生成。其中序贯Gibbs采样初始步长设置为0.5, 模拟退火初始温度为3 ℃, 终止温度为1 ℃。

图1 T2谱模型及贝叶斯成像结果 图2 NMR数据Fig.1 Model of T2 spectral and Bayesian imaging results Fig.2 NMR data
利用

(6)
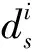
4条Markov链对应的NMR数据拟合的均方根误差(RMSE)如图3所示。可以看出经过2万次采样后, 4条链的RMSE均达到稳定。经过5万次采样后, 3条链的RMSE均在0.04以下, 其中第2条链的RMSE最小, 为0.24。同时给出了Chain 3对应的贝叶斯成像结果, 如图1中误差棒曲线所示, 误差棒为利用后1万次采样结果计算得到的不确定度。可以看出对随机模型, 基于贝叶斯方法得到的T2谱结果与模型基本一致, 不存在伪影, 仅在1~10 ms间5个T2值存在一定误差。

图3 NMR数据拟合误差 图4 贝叶斯成像数据误差概率统计 Fig.3 Fitting error of NMR data Fig.4 Probability statistics of data errors for Bayesian imaging
利用图1中Chain 3得到的贝叶斯T2谱成像结果, 计算得到对应的NMR数据如图2中实线所示, 可得出数据与仿真模型数据吻合度较高, 基本重合, 进一步验证了基于贝叶斯T2谱成像方法的有效性。
图4给出了NMR数据误差的统计结果, 如图4中直方图所示, 与仿真加入的高斯噪声的概率(虚线)分布一致。综上可以得出, 对T2随机模型, 贝叶斯方法能准确反应其T2谱分布。
3 结 语
笔者针对不均匀分布的随机的T2谱, 传统方法会导致部分细节丢失的问题, 研究了基于贝叶斯的核磁共振T2谱成像方法。该方法在贝叶斯理论的基础上, 构建NMR信号的似然函数及后验概率密度分布。并利用改进的Metropolis方法实现了T2谱的成像, 计算了成像结果的不确定度。最后, 通过对实验结果分析, 得出对应不均匀分布的随机的T2谱, 该方法不会导致细节的丢失。
参考文献:
[1]邓冬艳, 邓鹏翅, 宋红杰, 等. 核磁共振法测定蛋黄中磷脂酰胆碱含量的实验研究 [J]. 实验技术与管理, 2018, 35(10): 50-53.
DENG Dongyan, DENG Pengchi, SONG Hongjie, et al. Experimental Study on Determination of Phosphatidylcholine Content in Egg Yolk by NMR [J]. Experimental Technology and Management, 2018, 35(10): 50-53.
[2]任伟建, 于雪, 霍凤财, 等. 基于贝叶斯网络的油田管道失效概率计算 [J]. 吉林大学学报(信息科学版), 2021, 39(1): 66-76.
REN Weijian, YU Xue, HUO Fengcai, et al. Calculation of Failure Probability of Oil Field Pipeline Based on Bayesian Network [J]. Journal of Jilin University (Information Science Edition), 2021, 39(1): 66-76.
[3]张明. 基于贝叶斯网络的集中化IT运维信息检索算法 [J]. 吉林大学学报(信息科学版), 2021, 39(5): 576-582.
ZHANG Ming. Centralized IT Operation and Maintenance Information Retrieval Algorithm Based on Bayesian Network [J]. Journal of Jilin University (Information Science Edition), 2021, 39(5): 576-582.
[4]李宏磊, 丛玉良, 任柏寒. 基于隐朴素贝叶斯分类方法的垂直切换算法 [J]. 吉林大学学报(信息科学版), 2019, 37(3): 238-244.
LI Honglei, CONG Yuliang, REN Baihan. Adaptive Vertical Switching Algorithm Based on Hidden Naive Bayesian Classification [J]. Journal of Jilin University (Information Science Edition), 2019, 37(3): 238-244.
[5]胡云鹏, 王世刚. 基于支持向量机与朴素贝叶斯的犯罪度理论研究 [J]. 吉林大学学报(信息科学版), 2017, 35(1): 20-25.
HU Yunpeng, WANG Shigang. Research on Crime Degree Theory of Internet Speech Based on Support Vector Machine and Naive Bayes [J]. Journal of Jilin University (Information Science Edition), 2017, 35(1): 20-25.
[6]林君, 慧芳, 孙淑琴, 等. 基于不等式约束的磁共振信号T2谱多指数分解法及算法改进 [J]. 吉林大学学报(地球科学版), 2013, 43(6): 2018-2025.
LIN Jun, HUI Fang, SUN Shuqin, et al. MRS SignalT2Inversion by Multi-Exponential Decomposition with Inequality Constraint [J]. Journal of Jilin University (Earth Science Edition), 2013, 43(6): 2018-2025.
[7]杨玉晶, 叶瑞, 赵汗青, 等. 基于自旋回波探测的地面磁共振T_2谱正反演策略 [J]. 物理学报, 2021, 70(6): 186-196.
YANG Yujing, YE Rui, ZHAO Hanqing, et al. A Modeling and Inversion Method of Spin Echoes to Measure Magnetic Resonance Sounding Transverse Relaxation Time in Surface Applications [J]. Acta Physica Sinica, 2021, 70(6): 186-196.
[8]林峰, 王祝文, 刘菁华, 等. 核磁共振T2谱奇异值反演改进算法 [J]. 吉林大学学报(地球科学版), 2009, 39(6): 1150-1155.
LIN Feng, WANG Zhuwen, LIU Jinghua, et al. An Improved Algorithm for Singular Value Decomposition Inversion ofT2Spectrum in Nuclear Magnetic Resonance [J]. Journal of Jilin University (Earth Science Edition), 2009, 39(6): 1150-1155.
[9]陈珊珊, 汪红志, 杨培强, 等. 低场核磁共振弛豫谱反演算法研究 [J]. 生物医学工程学杂志, 2014, 31(3): 682-685.
CHEN Shanhan, WANG Hongjie, YANG Peizhi, et al. Study of the Algorithm for Inversion of Low Field Nuclear Magnetic Resonance Relaxation Distribution [J]. Journal of Biomedical Engineering, 2014, 31(3): 682-685.
[10]蒋川东, 常星, 孙佳, 等. 基于L1范数的低场核磁共振T_2谱稀疏反演方法 [J]. 物理学报, 2017, 66(4): 239-250.
JIANG Chuandong, CHANG Xing, SUN Jia, et al. Sparse Inversion Method ofT2Spectrum Based on theL1Norm for Low-Field Nuclear Magnetic Resonance [J]. Acta Physica Sinica, 2017, 66(4): 239-250.
[11]CHRISTIAN P, ROBERT GEORGE CASELLA. Monte Carlo Stastistical Methods [M]. New York, USA: Springer Verlag, 2004.
[12]余小东, 陆从德, 王绪本. 时间域航空电磁数据的自适应变维贝叶斯反演研究 [J]. 地球物理学进展, 2020, 35(5): 2023-2032.
YU Xiaodong, LU Congde, WANG Xuben. Adaptive Trans-Dimensional Bayesian Inversion of Airborne Time-Domain Electromagnetic Data [J]. Progress in Geophysics, 2020, 35(5): 2023-2032.
[13]刘辉, 李静, 曾昭发, 等. 基于贝叶斯理论面波频散曲线随机反演 [J]. 物探与化探, 2021, 45(4): 951-960.
LIU Hui, LI Jing, ZENG Zhaofa, et al. Stochastic Inversion of Surface Wave Dispersion Curves Based on Bayesian Theory [J]. Geophysical and Geochemical Exploration, 2021, 45( 4): 951-960.
[14]MOSEGAARD KALUS, TARANTOLA ALBERT. Monte Carlo Sampling of Solutions to Inverse Problems [J]. Journal of Geophysical Research, 1995, 100: 12431-12447.
[15]徐琳, 陈雨泽, 刘家昊. Monte-Carlo法模拟二维Ising模型----Metropolis、Swendsen-Wang与Wolff算法的对比 [J]. 大学物理, 2022, 41(1): 79-83.
XU Lin, CHEN Yuze, LIU Jiahao. Monte-Carlo Simulation of 2-D Ising Model-Application of Metropolis, Swendsen-Wang and Wolff Algorithm [J]. College Physics, 2022, 41(1): 79-83.
[16]李元香, 蒋文超, 项正龙, 等. 基于弛豫模型的模拟退火算法温度设置方法 [J]. 计算机学报, 2020, 43(11): 2084-2100.
LI Yuanxiang, JIANG Wenchao, XIANG Zhenglong. et al. Relaxation Model Based Temperature Setting Methods for Simulated Annealing Algorithm [J]. Chinese Journal of Computers, 2020, 43(11): 2084-2100.

