基于多尺度变形卷积的特征金字塔光流计算方法
范兵兵 葛利跃 张聪炫 李 兵 冯 诚 陈 震
光流是指图像序列中运动目标或场景表面像素点的二维运动矢量,其不仅包含了物体或场景的运动参数,还携带了图像中运动目标丰富的结构信息,因此,针对图像序列光流计算技术的研究一直是图像处理、计算机视觉等领域的研究热点.相关研究成果广泛应用于目标跟踪[1]、图像配准[2]、表情识别[3]、运动遮挡检测[4]和机器人视觉导航[5]等高级视觉任务.
自 Horn和 Schunck 提出变分光流计算技术以来,图像序列光流计算技术在光流计算精度和鲁棒性方面已经取得显著提升[6].然而,随着图像序列包含的场景任务日益复杂,光流计算的难度越来越大.例如,当图像序列中包含运动遮挡、大位移以及非刚性形变等困难复杂场景时,当前光流计算方法在精度与鲁棒性方面仍亟需进一步提高.特别在图像与运动边缘区域,现有光流计算方法普遍存在较为严重的信息丢失与模糊问题.针对该问题,传统变分光流计算方法通常采用在能量泛函中附加约束项[6]或设计边缘保护策略来改善该问题[7].例如,Zhang 等[8]提出一种基于三角网格的遮挡检测约束项并将其与变分能量泛函耦合,通过补偿光流计算中损失的遮挡信息,显著提升了图像与运动边缘区域光流计算精度.Mei 等[9]将局部优化策略与全局优化策略相结合,提出一种局部与全局耦合的加权正则变分光流计算模型,提高了光照变化场景光流计算的精度与鲁棒性.针对大位移运动场景光流计算准确性较低问题,Chen 等[10]将块匹配策略与由粗到细的光流计算方案相结合,提高了大位移运动光流计算精度,但该方案易导致边缘模糊和细节结构信息丢失.为此,Deng 等[11]提出一种新颖的可微邻域搜索上采样模块,并将其与由粗到细光流计算方案结合,较好地保护了图像与边缘结构.后续,文献[12] 在光流金字塔分层优化过程中集成结构引导滤波,利用结构引导滤波具有边缘保护的作用,实现光流计算运动边缘的保护.Dong 等[13]进一步将滤波技术与非局部项相结合,提出一种非局部传播的滤波光流优化方案,在减少光流计算异常值的同时保留了丰富的上下文信息.
近年来,随着人工智能与深度学习技术的飞速发展,基于深度学习的光流计算技术得到广泛关注.Dosovitskiy 等[14]率先将卷积神经网络引入光流计算,提出 FlowNet 深度学习光流计算模型,该模型通过采用编码-解码结构极大地缩短了光流计算所需的时间,同时也奠定了深度学习光流计算网络的基本结构.然而,FlowNet 的网络结构比较简单,光流计算精度较低.后续,Ilg 等[15]将FlowNet 网络结构进行多次堆叠,并将堆叠后的网络命名为 Flow-Net 2.0,与 FlowNet 相比,FlowNet 2.0 网络深度更深,光流计算精度也更高.但多次堆叠操作使得FlowNet 2.0 网络结构过于臃肿复杂,模型训练不仅困难而且易陷入过拟合.为了在光流计算精度与模型尺寸之间寻求平衡,Sun 等[16]将特征金字塔、变形操作、成本体积代价集成在统一的光流计算网络框架中,提出 PWC-Net 光流计算方法.该方法在简化网络尺寸的同时大幅提高了光流计算的精度与鲁棒性.然而,上述方法均为有监督深度学习光流计算方法,需要提供大量具有真实标签的样本数据用于模型训练,因此难以应用于真实任务场景.受传统变分光流中的能量泛函启发,Yu 等[17]通过设计基于数据项与平滑项相结合的损失函数,实现了基于无监督学习的光流计算.这在一定程度使深度学习光流计算模型摆脱了对标签样本数据的依赖,但光流计算精度大幅落后于有监督学习方法.为此,Liu 等[18]借鉴知识蒸馏思想,提出一种基于数据驱动的蒸馏学习无监督光流计算模型 DDFlow.该方法通过数据驱动自动学习和预测光流,在提高光流计算精度的同时实现了实时无监督光流计算.
现阶段,基于深度学习的光流计算方法虽然已取得较大进展,光流计算精度不断提高.但是,由于大位移、运动遮挡以及非刚性运动违背了网络模型设计的先验知识,因此光流计算在图像与运动边缘区域存在模糊的问题仍未得到妥善解决.Hur 等[19]通过引入遮挡真实值,设计一种遮挡解码器对遮挡区域特征学习并利用学习到的遮挡信息约束遮挡区域的光流计算,一定程度缓解了该问题.然而,包含遮挡真实值的数据集较少,难以满足大规模使用.为了克服该问题,Zhao 等[20]提出一种不需要遮挡真实值的非对称特征匹配模块学习遮挡掩膜,以约束遮挡区域光流计算.Meister 等[21]借鉴变分遮挡光流计算策略,设计一种前后一致性损失函数用于指导网络学习遮挡特征信息,有效保护了图像与运动边缘.
当前,基于深度学习的光流计算网络模型大多都致力于研究新的先验知识来设计光流计算网络结构.然而,相对于之前的网络,这些网络结构往往非常复杂且难以训练,不仅大幅增加了深度学习光流计算的难度,而且还进一步提高了计算成本.针对上述问题,本文从图像特征提取网络模型的设计入手,提出一种基于多尺度变形卷积的特征提取模型,并将其与特征金字塔光流计算网络耦合,在少量增加原有网络结构复杂度的同时提高编码器网络的特征提取能力,从而获取更加准确的图像特征.此外,为了保护图像与运动边缘,本文又设计一种结合图像与运动边缘约束的混合损失函数,来指导模型学习更加精准的边缘信息.实验结果证明,本文方法具有更高的光流计算精度,有效解决了光流计算的边缘模糊问题.
1 基于多尺度变形卷积的特征金字塔光流计算模型
1.1 多尺度变形卷积特征提取网络
当前,深度学习光流计算网络模型普遍采用标准卷积实现图像特征提取.然而,标准卷积具有较为显著的平滑作用,导致提取的图像特征过于平滑.同时,标准卷积对规则区域的特征信息捕获较为准确,在不规则区域往往无法获取完整的图像特征.因此,仅利用标准卷积构建图像特征提取网络难以获取准确的图像特征信息.
针对该问题,本文从图像特征提取策略出发,提出一种多尺度变形卷积特征提取网络.通过聚合多尺度图像特征信息,让多尺度变形卷积感受野可以拟合不同尺寸和形状的目标,从而更加精准地提取出图像特征.图1 展示了标准卷积与变形卷积在运动目标翅膀区域图像特征提取示意图与对应模型光流计算结果.从图1(a)、图1(b) 中可以看出,标准卷积相对变形卷积捕获了更多非目标的像素点信息,而变形卷积通过拟合翅膀区域形状捕获了更加准确的图像特征,特别是边缘区域更贴近真实图像边缘.图1(c)和图1(d) 分别展示了使用两种卷积提取特征后的模型光流计算结果,图中右上角为光流真实值.从图中可以看出,在运动目标的翅膀区域,使用变形卷积提取特征的光流计算结果与真实值更加接近且未出现中断.而使用标准卷积的光流计算结果在翅膀区域与真实值存在较大差异且存在明显的中断.说明变形卷积通过拟合翅膀区域形状捕获更加准确的图像特征信息,对提高光流计算的精度具有较好的促进作用.
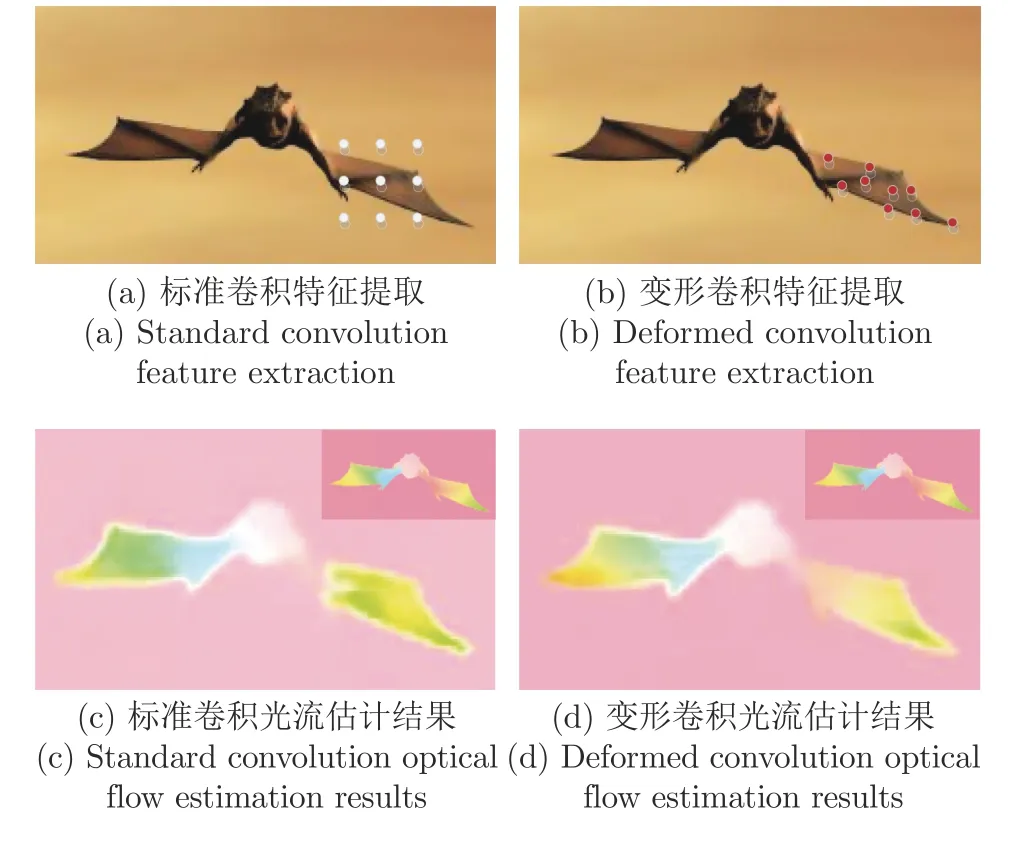
图1 标准卷积与变形卷积图像特征提取示意图与对应模型光流计算结果Fig.1 Schematic diagram of standard convolution and deformed convolution image feature extraction and corresponding model optical flow estimation results
图2 展示了本文所提的多尺度变形卷积特征提取网络结构示意图.从图中可以看出,在输入原始图像序列后,首先使用标准卷积获取稠密的初始图像特征,该步骤一定程度起到图像预处理作用.然后,使用不同尺度的变形卷积对稠密的初始图像特征进行细化,以提取不同尺寸的目标特征信息.其中,变形卷积特征提取网络包含3 条并行的分支,每条分支均包含1 个变形卷积层.且变形卷积核尺寸分别为 3×3、5×5和 7×7,每条分支的输出均为12 通道的特征图.最后,对每个变形卷积提取的特征使用 3×3 标准卷积,并通过1 个标准 3×3 卷积层将每条分支的输出特征图进行通道拼接,以聚合所有分支捕获的图像特征信息.由于在连续帧的图像序列中,即使是相同运动目标,它的大小和形状也有可能不同.因此,本文通过引入变形卷积使卷积层的感受野可以灵活改变,以适合运动目标不同的大小和形状,从而获取不同范围内不同尺度的图像特征信息.

图2 多尺度变形卷积特征提取网络结构示意图Fig.2 Schematic diagram of multi-scale deformed convolution feature extraction network structure
在图2 中虚线方框区域,本文先使用变形卷积再使用标准卷积的原因有两方面:一方面,尽管变形卷积对目标有更好的适应性,但是在多尺度特征提取网络模型中,随着图像尺度的减小,图像中目标的形态轮廓信息逐渐损失变得模糊.此时变形卷积难以准确地拟合不同尺寸和形状的目标,并且随着拟合精度的下降还会引入大量噪声与异常值.因此,为了缓解进而改善该问题,本文在变形卷积之后对应增加了 3×3 标准卷积操作,其作用是在提高低分辨率特征提取精度的同时进行滤波以去除提取特征中的噪声与异常值.另一方面,变形卷积由于具有拟合不同尺寸和形状的目标的特性,因此,变形卷积相对传统卷积包含更多的参数.如果单一使用变形卷积构建多尺度特征提取模型将大幅增加模型尺寸,训练参数也将大幅增加,导致模型训练困难,难以收敛拟合.
将上述过程公式化:令Fin表示多尺度变形卷积特征提取网络的输入,多尺度变形卷积特征提取网络的3 条平行分支的输出计算公式可以表示为

式 (1) 中,F1,F2,F3分别代表第1、2、3 条分支的输出,运算符号 C onv1,C onv2,C onv3代表第1、2、3条分支的标准卷积运算,运算符号 D econv1,D econv2,Deconv3代表第1、2、3 条分支对应的变形卷积运算,运算符号 C onv 代表3 条并行分支之前的标准卷积运算.将各条分支的输出特征拼接起来进行信息聚合,多尺度变形卷积特征提取网络的最终输出可以表示为

式(2)中,C onvf是一个 3×3 标准卷积,代表最终聚合信息的卷积操作,c oncatenate 是通道拼接操作.图3 展示了本文方法特征提取结果与仅使用标准卷积特征提取结果的可视化对比,其中,标签A、B、C 分别对应运动目标不同的三个边缘区域.从图3(e)中可以看出,仅使用标准卷积构建的多尺度特征提取网络模型,所获取的图像特征在边缘区域明显模糊,且异常值较多.而本文所提的多尺度变形卷积特征提取网络获取的图像特征在边缘区域更为清晰,异常值与噪声也较少,并且获取的图像特征值更大.

图3 本文方法特征提取与标准卷积特征提取结果可视化对比Fig.3 Visual comparison of feature extraction results of the method in this paper and standard convolution feature extraction results
1.2 基于多尺度变形卷积的特征金字塔光流计算网络
本文将多尺度变形卷积特征提取网络与特征金字塔光流计算网络耦合,构建基于多尺度变形卷积的特征金字塔光流计算模型,以实现高精度的光流计算.图4 展示了本文提出的基于多尺度变形卷积的特征金字塔光流计算网络模型.从图中可以看出,网络模型主要由编码器网络与解码器网络组成.其中,编码器网络由基于多尺度变形卷积的特征提取网络和编码器组成.解码器网络由解码器和上下文信息聚合网络组成.在光流计算过程中,首先将连续两帧图像输入多尺度变形卷积特征提取网络进行图像特征提取,然后将获取的图像特征输入下采样因子为0.5 的编码器进行更加细化的特征提取.最后,从最小分辨率特征图所在的金字塔顶层计算相关度,并将相关度输入解码器计算光流.
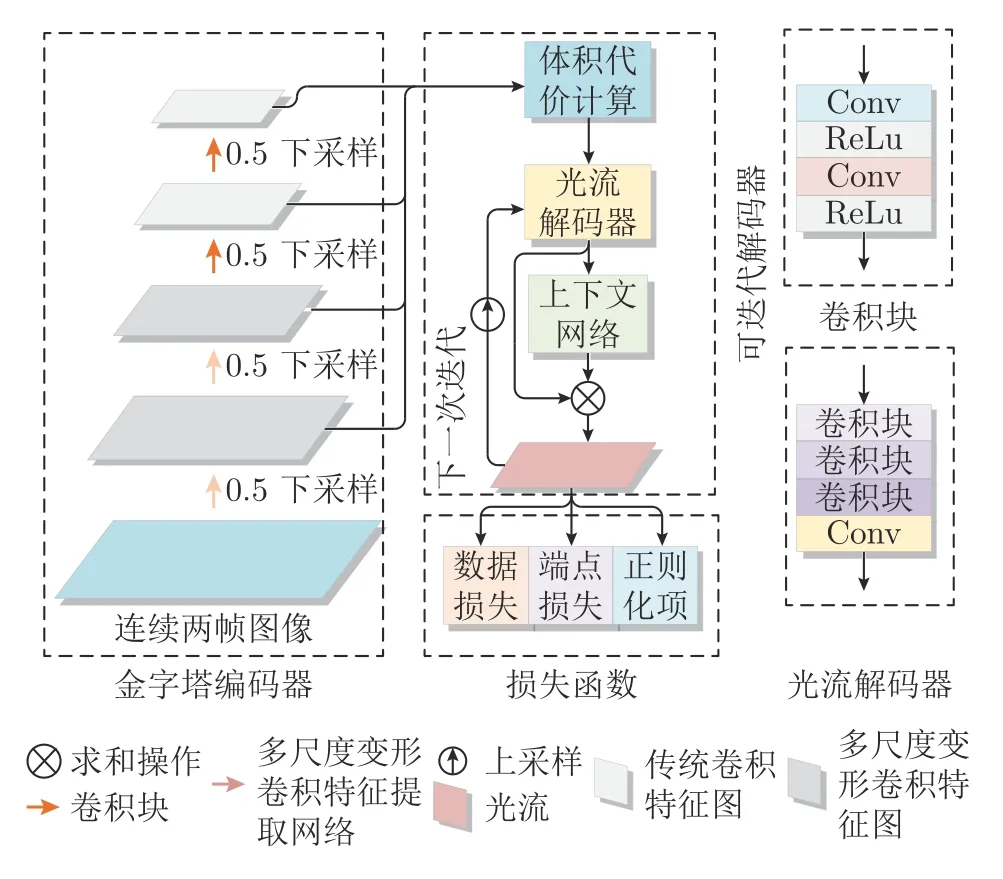
图4 基于多尺度变形卷积的特征金字塔光流计算网络模型Fig.4 Feature pyramid optical flow computing network model based on multi-scale deformed convolution
在金字塔的每一层,本文首先计算第一帧图像特征图与第二帧经上一层光流变形后的特征图的相关度,然后通过光流解码器计算该层的光流,并使用上下文网络进行优化.该层光流经过上采样后作为初始光流送入金字塔下一层,进行下一层的光流计算.经过对应特征金字塔层数的迭代后,模型将输出原分辨率1/4 大小的光流计算结果,最后通过插值上采样运算,将光流计算结果恢复为输入图像的原始分辨率.
在实际计算过程中,本文只在分辨率最大的底部两层使用了多尺度变形卷积特征提取网络.这是因为变形卷积改变感受野是通过偏置因数来实现的,偏置因数对运动目标的轮廓较为敏感,而下采样操作会丢失图像中大量的空间信息,使得运动目标轮廓会变得模糊,甚至丢失.图5 展示了不同层数多尺度变形卷积对光流计算在运动边缘的影响.图中标签区域为边缘轮廓区域与其对应放大图.从图中可以看出,使用4 层多尺度变形卷积模型与使用2 层多尺度变形卷积模型相比,其光流计算结果在标签区域中的手部存在明显的模糊与边缘扩张,手指边缘轮廓计算效果明显低于使用2 层多尺度变形卷积模型的光流计算效果.因此,本文只在分辨率最大的底部两层使用,以发挥多尺度变形卷积特征提取的能力,提高运动边缘处光流计算精度.

图5 不同层数多尺度变形卷积模型光流计算结果对比Fig.5 Comparison of optical flow calculation results of multi-scale deformed convolution models with different layers
2 混合损失函数
现阶段,大部分深度学习光流计算网络模型的损失函数由端点误差函数构成.由于端点误差损失函数更关注光流计算的整体效果,难以对运动边缘区域进行引导训练,导致光流计算结果易产生边缘模糊现象.为了约束运动边缘处光流计算,本文设计了一种结合图像与运动边缘约束的混合损失函数,该损失函数由端点误差损失、数据项损失以及根据图像与运动边缘控制光流扩散方式的正则化项共同组成.计算公式如下

式 (3) 中,Lepe代表端点误差,Ldata代表数据项损失,Lsmooth代表正则化项 (平滑项).端点误差的计算公式如下
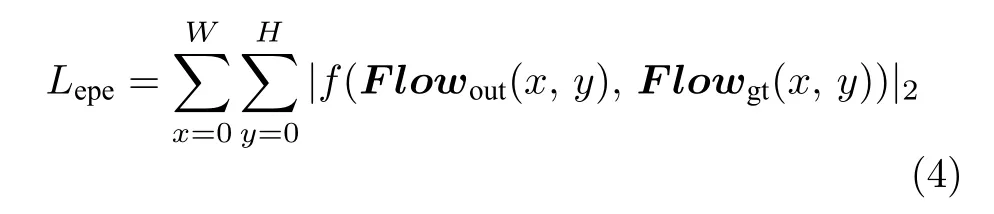
式 (4) 中,Flowout(x,y)和Flowgt(x,y) 分别代表光流计算值和真实值在像素点坐标 (x,y)T处的值,|·|2代表L2范数运算.f(x,y) 是一种广义的鲁棒 Charbonnier 惩罚函数,主要作用是惩罚异常值,计算公式如下

为了使惩罚函数能够发挥最佳性能,本文依据文献[22]的参数设置方法,将参数ε和κ分别设置为ε=0.001,κ=0.4.
数据项损失计算公式如下

式 (6) 中,X=(x,y)T表示在图像区域 Ω 中的像素点坐标,I(X+F lowgt(X),t+1) 代表使用真实光流值变形的第二帧图像在像素点X处的亮度值.I(X+F lowout(X),t+1)代表使用计算光流值变形的第二帧图像在像素点X处的亮度值.真实光流与计算光流变形第二帧图像时,通常会在错误的光流计算区域出现较大差别,因而使用数据损失的目的是对错误的大位移运动区域进行二次监督,以提高模型的光流计算精度.
正则化项计算公式如下

式 (7) 中,∇d表示在d方向上进行求导,α是控制光流平滑的边缘系数,I(t) 是第一帧图像的亮度值.正则化项通过控制光流的扩散形式保护运动边缘,当运动边缘处的图像导数较大时使 e-α|∇dI(t)|变小,以减少光流扩散,从而保护运动边缘.当运动边缘处的图像导数较小时使 e-α|∇dI(t)|变大,以增加光流扩散程度,保护背景光流.通过将该正则化项与端点误差损失、数据项损失联合指导光流计算模型训练,使模型学习到更加精准的边缘信息.
图6 展示了使用不同损失函数对模型训练的影响.从图中可以看出,使用数据项与平滑项作为损失函数训练模型,可以引导模型收敛但模型收敛速度较慢,收敛效果不佳.其原因在于数据项与平滑项组成的损失函数参考了变分光流能量泛函的设计,其在最小化过程中需要一定的迭代计算且易陷入局部最优,因而收敛速度较慢,收敛效果也相对较差.使用端点误差损失函数训练模型,模型收敛速度和收敛效果优于数据项与平滑项损失函数.其原因是端点误差损失本质上就是求解计算值与真实值之间的最小误差,其计算过程简单、耗时较少且又有真实值作为参考,所以收敛效果优于前者.使用本文所提的混合损失函数训练模型,模型整体不仅收敛速度较快,而且收敛效果也明显优于前两种损失函数.因此,通过将端点误差损失、数据项损失与平滑项损失结合,既可以加快模型收敛速度又可以提高模型训练效果.

图6 不同损失函数训练模型Fig.6 Training models with different loss functions
为了展示混合损失函数不同组成部分对边缘区域的保护效果,图7 展示了不同损失函数训练模型后的光流计算结果可视化对比.其中,图中第二行为第一行图像标签区域的局部放大图.从图中可以看出,使用数据项与平滑项损失函数训练后的模型光流计算结果可以计算出目标的完整轮廓与边缘,但结果中包含较多异常值且存在明显的模糊现象.使用端点误差损失函数训练后的模型光流计算精度相对较高,但仍然存在较为明显的边缘模糊,例如图7(d) 中的A 区域.而使用混合损失函数训练后的模型光流计算结果达到了最佳的光流估计效果,特别在标签区域的边缘,既消除了异常值又实现了高精度的边缘保护.说明将端点误差损失、数据项损失与平滑项损失结合用于模型训练,不仅可以加快模型收敛速度,还可以学习到更多边缘信息.
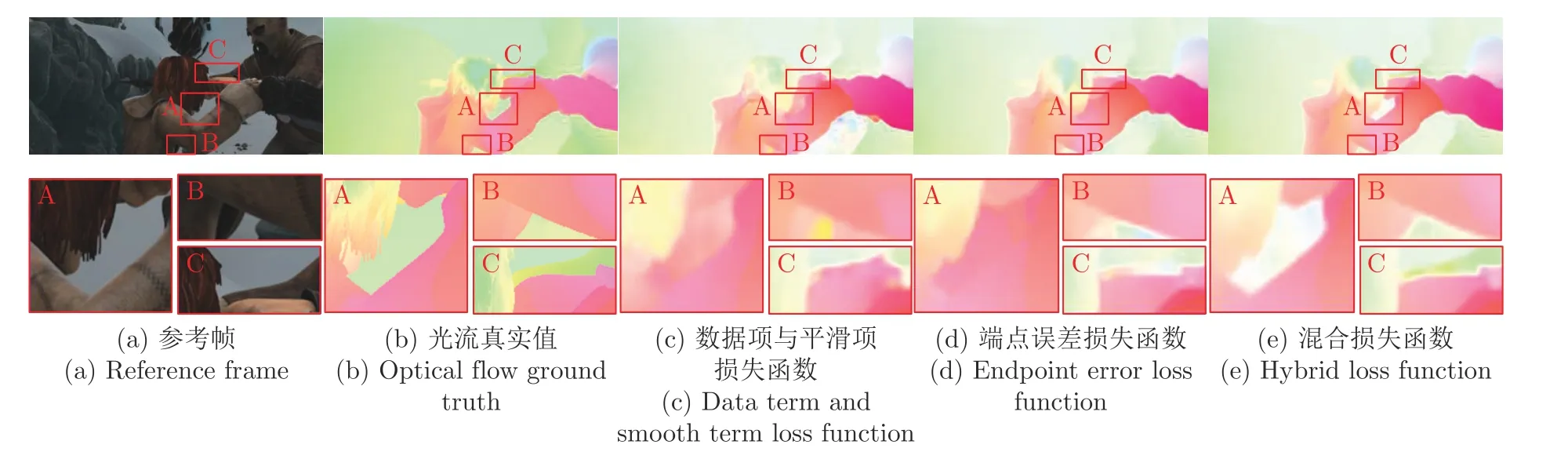
图7 不同损失函数训练模型后的光流计算结果可视化对比Fig.7 Visual comparison of optical flow calculation results after training models with different loss functions
3 实验与分析
3.1 评价指标
实验采用当前光流计算技术研究领域内具有权威性的 MPI-Sintel[23]与 KITTI2015[24]测试图像数据集进行算法性能测试.分别采用端点误差和异常值百分比两种量化评价指标对本文方法光流计算的准确性和鲁棒性进行量化评价.其中,端点误差是光流计算领域评价光流精度最常用的一种指标,表示的含义是计算光流与真实光流的几何距离误差.其计算公式如下

上式中,N是整张图像中总的像素点数量,ugt是水平方向上的真实光流值,uout是水平方向上的计算光流值,vgt是垂直方向上的真实光流值,vout是垂直方向上的计算光流值.
异常值百分比指标常用于 KITTI2015 测试图像数据集的光流计算结果评价,计算公式如下
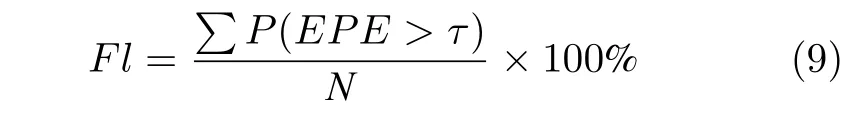
式中,N是整张图像中总的像素点数量,Fl表示光流异常值百分比,P(EPE >τ) 表示光流端点误差大于τ的像素点,其中τ=3.
3.2 对比方法
为了验证本文方法光流计算精度和边缘保护效果,分别选取具有代表性的 FlowNet 2.0[15]、PWCNet[16]、IRR-PWC_RVC[19]、FastFlowNet[25]、Lite-FlowNet[26]、FlowNet3[27]、Semantic_Lattice[28]、OAS-Net[29]、LSM_RVC[30]以及 FDFlowNet[31]等深度学习光流计算方法进行综合对比分析.其中,FlowNet 2.0 通过堆叠多个 FlowNet 结构提高网络深度,成为首个超越传统变分光流计算精度的深度学习光流计算方法.PWC-Net 通过将特征金字塔、变形操作以及成本体积代价集成于统一框架,在简化网络结构减少训练参数的同时显著提升了光流计算精度.IRR-PWC_RVC 是首个采用遮挡真实值计算遮挡掩膜来提高遮挡区域光流计算精度的方法.FastFlowNet 采用新的增强池化金字塔特征提取器增强高分辨率金字塔特征,并引入中心密集扩张相关层构建紧凑的代价量,在保持精度的同时极大地提升了光流计算速度.LiteFlowNet 通过使用短程匹配产生一个光流场对原始光流场进行优化,提高了大位移运动区域的光流计算精度.FlowNet3 将遮挡、光流和视差进行联合学习,提出了一种有效的可学习的遮挡区域计算方法,不仅大幅提高光流计算精度也有效保护了运动边缘.Semantic_Lattice 定义了一种广义的卷积方式,并将这种广义的卷积方式应用到解码器中减少边缘伪影,保护光流的运动边缘.OAS-Net 提出了一个新的遮挡感知采样模块,抑制噪声对遮挡区域的影响,从而提高遮挡区域的光流计算精度,以实现光流运动边缘保护.LSM_RVC 提出了学习子空间最小化框架,利用卷积神经网络生成一个子空间约束取代正则化项,增强了网络模型的泛化能力.FDFlowNet 使用 U 形网络融合特征代替原有的金字塔特征,并提出一种新的局部全连接结构,平衡了模型的尺寸、计算成本和网络性能,显著提升了光流计算精度与速度.
3.3 MPI-Sintel 测试图像数据集实验
MPI-Sintel[22]测试图像数据集是一种开源的合成光流数据集,包含了大位移、运动遮挡以及非刚性大形变等困难场景.该测试集分为 Clean和 Final两个数据集,其中 Final 数据集相对 Clean 数据集包含了大量的运动模糊、光照变化以及大气效果等挑战性元素,光流计算难度较大.表1 展示了本文方法与对比方法针对 MPI-Sintel 测试图像数据集的光流计算结果.其中,All 代表所有像素点的平均端点误差,Matched 代表图像序列中非遮挡像素点的端点误差,Unmatched 代表图像序列中遮挡像素点的端点误差.
从表1 可以看出,本文方法在 Clean和 Final子数据集的 All和 Matched 指标上均取得了最优表现,IRR-PWC_RVC 在 Unmatched 指标取得最佳的光流计算精度.OAS-Net 方法在 Clean 数据集的光流估计精度除低于本文方法外,整体性能优于其他对比方法,这源于该模型的遮挡感知采样模块既抑制了噪声又提高了遮挡区域的光流估计精度.在 Final 数据集上,IRR-PWC_RVC 方法的光流计算精度与本文方法接近,主要原因是 IRRPWC_RVC 方法在图像特征提取骨干网络中引入遮挡检测模块,通过在特征提取的过程中加入遮挡信息以补偿运动遮挡产生的信息丢失,进而提高图像特征提取精度.此外,该方法在端点误差损失函数的基础上设计了一种包含遮挡损失项的复合损失函数,使得遮挡信息能够引导模型得到充分训练.本文方法通过构建多尺度变形卷积图像特征提取模型,并设计包含边缘结构信息的混合损失函数,使得光流估计模型的特征提取精度与边缘保护效果得到有效改善.二者的相同点在于都遵循了相似的网络模型设计思路,通过提高图像特征提取精度和利用率的方式实现高精度光流估计.区别在于本文方法侧重于光流边缘结构的保护,而 IRR-PWC_RVC方法关注于遮挡区域光流信息的获取.因此,虽然本文方法与 IRR-PWC_RVC 方法的光流估计精度相近,但两种方法提高光流估计性能的具体方式和侧重点具有很大区别.
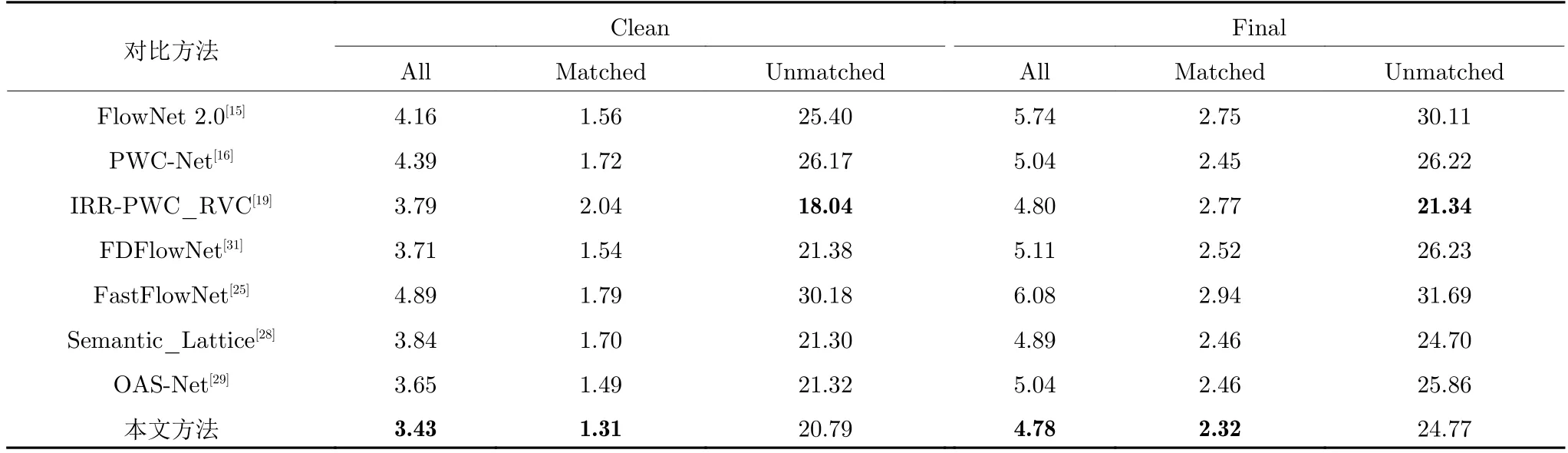
表1 MPI-Sintel 数据集图像序列光流计算结果Table 1 Optical flow calculation results of image sequences in MPI-Sintel dataset
上述指标从宏观角度对比了各方法光流计算性能,为了更加细化地对各方法光流计算效果进行对比分析,本文使用 MPI-Sintel 测试图像数据集提供的 d0-10,d10-60,d60-140以及 s0-10,s10-40,s40+指标进行量化对比分析.其中,d0-10,d10-60,d60-140代表距离运动边缘不同距离像素点的端点误差,s0-10,s10-40,s40+代表不同位移速度像素点的端点误差.实验结果如表2 所示,从表2 可以看出,针对 Clean 子数据集,本文方法在 d0-10,d10-60,d60-140等衡量运动边缘光流计算效果的指标上取得了最佳的光流计算精度.在挑战性较大的 Final数据集,本文方法在 d0-10,d10-60,d60-140指标上的整体性能仍然优于其他对比算法.说明本文方法在运动边缘区域具有较高的光流计算精度与鲁棒性.此外,在 Clean 数据集的 s10-40,s40+指标和Final 数据集的 s10-40指标也显著优于对比方法,说明本文方法针对大位移运动场景也具有较高的光流计算精度.但在 s0-10指标上,本文方法未取得最优的光流计算精度,这说明在小位移运动光流计算方面,本文方法仍然存在一定限制.此外,在具有挑战性的 Final 数据集,本文方法在 d60-140和 s40+指标存在一定性能下降,产生该现象的原因可能是图像序列中的运动模糊效果导致本文方法难以捕捉更加精准的像素运动信息.
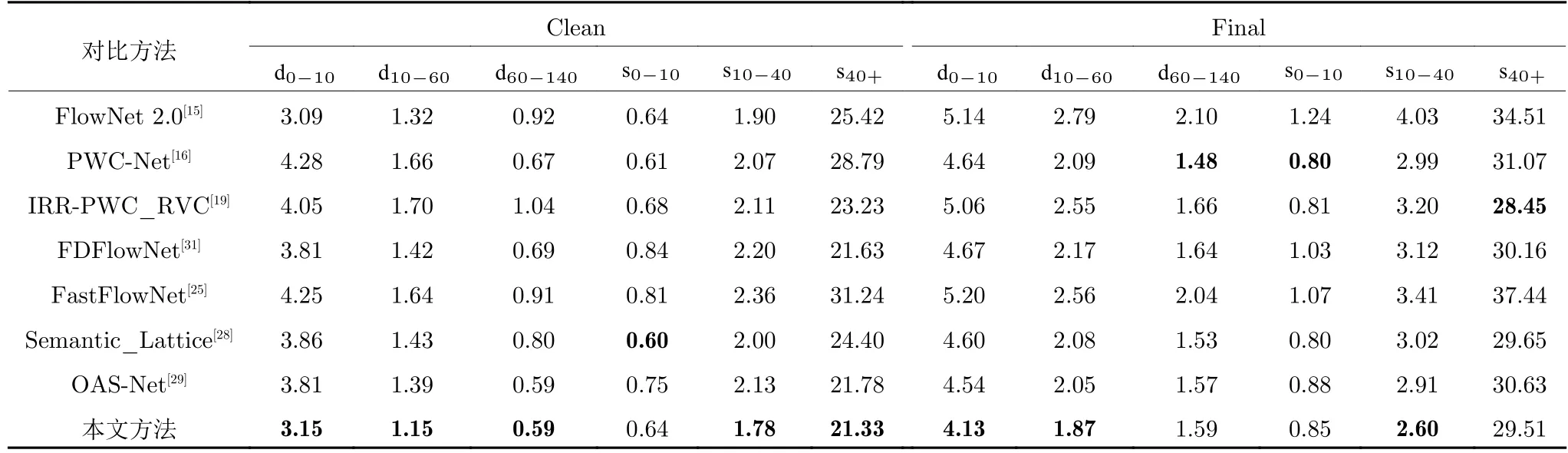
表2 MPI-Sintel 数据集运动边缘与大位移指标对比结果Table 2 Comparison results of motion edge and large displacement index in MPI-Sintel dataset
为进一步定性对比分析本文方法光流计算效果,本文分别选取如图8 所示的图像序列进行光流结果可视化展示.其中方框区域为典型的运动边缘区域,并且为了便于观察对比,本文对该区域进行局部放大.从图中可以看出,FlowNet 2.0 光流计算结果在运动边缘区域呈现过度平滑,这是因为FlowNet 2.0 堆叠了多个包含大量标准卷积操作的FlowNet 结构所致;PWC-Net 光流计算结果存在明显边缘扩张;OSA-Net 光流计算精度较高,但在Bamboo3 人物身体和 Market4 龙的尾部区域光流计算存在明显的错误估计;IRR-PWC_RVC 方法在标签区域存在明显信息丢失.与各对比方法相比,本文方法光流计算精度最优,特别在 Ambush3 标签区域、Bamboo3 人物的身体区域、Cave3 龙角处、Market1 人腿部区域和 Market4 龙的尾部区域,本文方法不仅更加准确地计算出上述区域光流信息,而且还有效缓解了运动边缘模糊问题.

图8 MPI-Sintel 数据集光流结果可视化对比图Fig.8 Visualization comparison of optical flow results in MPI-Sintel dataset
3.4 KITTI2015 测试图像数据集实验
KITTI2015[23]测试图像数据集是包含大量真实道路场景的数据集,其主要用于测试算法针对真实场景任务时光流计算的准确性与鲁棒性.因此,对算法的性能要求较高,挑战性更大.表3 展示了本文方法与对比方法针对 KITTI2015 数据集图像序列光流计算异常值百分比结果对比.表中 Fl-bg代表图像中背景光流异常值百分比,Fl-fg 代表图像中前景光流异常值百分比,Fl-all 代表图像中平均光流异常值百分比.从表3 可以看出,FlowNet 2.0光流计算精度最低,说明仅通过堆叠网络提高模型深度方式,难以应对真实复杂场景光流计算的需求.LSM_RVC 光流计算精度与本方法较为接近,但在Fl-fg 指标误差明显高于本文方法.相对于其他方法,本文方法整体光流计算精度较高,仅 Fl-fg 指标略低于对比方法,产生该现象的原因是真实场景包含较为强烈的光照变化与阴影等情况,使得运动目标轮廓信息发生一定变化,致使本文方法所使用的变形卷积在拟合目标形态时产生一定的偏差.为了验证本文方法针对真实场景图像序列光流计算在运动边缘区域的保护效果,选取 KITTI2015 数据集中具有代表性的4 帧连续图像序列对本文方法和对比方法进行综合对比.

表3 KITTI2015 数据集计算结果Table 3 Calculation results in KITTI2015 dataset
图9 展示了本文方法与各对比方法针对测试图像序列的光流计算误差可视化对比,标签区域为运动边缘区域.为了更好地观察图中各对比方法在运动边缘区域光流计算效果,本文对标签区域进行了局部放大.从图中可以看出,在光照不足且边缘轮廓信息缺乏的 KITTI15_000000 序列,本文方法取得了最佳的光流计算效果,在汽车边缘轮廓区域异常值面积占比最小.在 KITTI15_000005 序列,本文方法在左侧汽车顶部区域光流计算效果较好,FlowNet3 在右侧白色背景区域取得了最佳的光流计算效果,说明本文方法针对缺乏纹理信息的场景光流计算存在一定限制.在包含大位移运动的KITTI15_000006和 KITTI15_000014 序列,本文方法取得了最佳的光流计算精度,特别在汽车边缘轮廓区域包含了较少的异常值.说明在真实场景光流计算中,本文方法仍然能够表现出较高的光流计算准确性,且对运动边缘具有较好的保护效果.

图9 KITTI2015 数据集光流误差结果对比图Fig.9 Comparison of optical flow error results in KITTI2015 dataset
表3 列出了本文方法与对比方法在 KITTI2015数据集的平均光流计算时间.从表3 中可以看出,FDFlowNet 方法的计算效率最高,本文方法提出的多尺度变形卷积特征提取网络由于使用了较多变形卷积操作,因此时间消耗相对较长.在基于深度学习的光流计算中,随着网络复杂度和参数量的增加,光流估计模型往往牺牲计算效率换取光流计算精度的提高,而本文方法在不大幅增加时间消耗的基础上显著提升了光流计算精度,综合性能较优.
3.5 消融实验
为了进一步分析本文提出的多尺度变形卷积特征提取网络模型和混合损失函数对光流计算性能提升的作用,本文采用消融实验进行综合对比分析.实验采用 MPI-Sintel 数据集中的 Clean 子数据集对各消融实验模型进行测试对比分析,各消融实验模型实验数据结果如表4 所示.其中,baseline 为基准模型,baseline_loss 为基准模型加混合损失函数模型,baseline_md 为基准模型加多尺度变形卷积特征提取网络模型,full model 是基准模型加上混合损失函数和多尺度变形卷积特征提取网络模型.从表4 可以看出,相比于单独去除多尺度变形卷积特征提取网络的 baseline_loss 模型和单独去除边缘损失函数的 baseline_md 模型,全模型在Clean 数据集的所有指标上取得了最好的光流计算效果.并且从 d0-10,d10-60,d60-140运动边缘指标可以看出,通过分别增加多尺度变形卷积特征提取网络和混合损失函数,可以有效提升光流运动边缘计算精度.当多尺度变形卷积特征提取网络与混合损失函数共同作用时,可以显著提高网络光流计算精度,二者的协同作用进一步提升了 d60-140指标精度.这进一步说明,本文所提方法各模块可以有效提高网络的光流计算精度,保护运动边缘.此外,从baseline_loss 模型数据可以看出,在全模型之外,该模型得到了最高的光流计算精度.反映出本文提出的混合损失函数对模型光流计算精度的提升具有明显的积极作用.

表4 MPI-Sintel 数据集上消融实验结果对比Table 4 Comparison of ablation experiment results in MPI-Sintel dataset
同样,为了更直观地展示各模块的工作性能,同时,定性分析本文提出的模型各组成模块对光流计算运动边缘的保护效果.本文将消融实验中各模型针对 Cave3 序列光流计算结果进行可视化对比,结果如图10 所示.其中,图10 中标签区域为图像序列场景中对应的图像与运动边缘区域.从图10中可以看出,本文方法所提各模块在去除异常值方面均具有较好的效果,相对于 baseline 模型较为准确地计算出人腿部附近区域的光流信息.同时,本文提出的各模块对于图像与运动边缘区域光流计算精度均具有明显提升.例如,图中龙角与人物腿部的中间区域图像边缘模糊现象得到有效抑制,并且光流估计结果边缘结构更加清晰.这也从侧面说明本文提出的多尺度变形卷积特征提取网络可以捕获更加准确的图像特征信息,所提出的混合损失函数能够更好地约束运动边缘区域的光流计算.

图10 各消融模型光流计算结果可视化对比图,第2、4 行为标签区域放大图Fig.10 Visual comparison of optical flow calculation results for each ablation model,the second and fourth rows are enlarged images of the label area
4 结论
本文通过构建多尺度变形卷积特征提取网络并将其与特征金字塔光流估计网络模型耦合,提出了一种基于多尺度变形卷积的图像序列光流计算方法.该方法首先通过多尺度变形卷积特征提取网络获取准确的图像特征信息.然后,设计了一种新的混合损失函数,将图像与运动边缘约束正则化项、数据项损失和端点误差结合,用以指导网络模型学习更加精准的图像与运动边缘信息,使损失函数可以更好地约束图像与运动边缘区域光流计算.通过大量实验对比分析,表明本文方法具有较高的光流计算精度,特别在运动边缘区域具有较好的保护效果.

