考虑全局和局部帕累托前沿的多模态多目标优化算法

李文桦 明梦君 张 涛,2 王 锐,2 黄生俊,2 王 凌

多目标优化问题 (Multi-objective optimization problems,MOPs) 在现实世界中广泛存在[1].对于该类优化问题,往往需要考虑存在互斥关系的多个优化目标,并且不存在一个解能够最优化所有优化目标.因此该类问题的最优解通常为一组互不支配的Pareto 最优解集.在工业应用和现实工程问题中,决策者经常遇到多个不同的最优解其目标函数值相同的一类问题,例如脑功能成像[2]、柴油机设计问题[3]、游戏地图生成问题[4]等.对于Pareto 前沿上的某个目标向量,在决策空间中可以找到多个对应的决策向量.这类问题通常称为多模态多目标优化问题[5](Multimodal multi-objective optimization problems,MMOPs).图1 展示了一个两目标两决策变量的MMOP,从中可以看到,A点和B点都对应于Pareto 前沿上的P点.对于决策者来说,如果能够获得待优化问题的全部最优解,一方面可以更深入地了解该问题,对于刻画问题属性、提出改进方向、寻找最优解等具有重要作用;另一方面,一旦其中一个最优解因环境变化等因素导致不可用,决策者可以方便快速地转变到另一个最优解.对于工业生产来说,多个最优解意味着有更多的生产方案可供选择.在某些情况下,决策者甚至会接受目标值稍劣的解[6].例如某个解决方案要达到的加工条件较为苛刻,或者对加工精度要求极高,那么决策者将偏向于选择对条件要求不苛刻的解而接受其目标函数值上的劣势.因此,如何获得MMOPs的全部最优解成为亟待解决的问题之一.

图1 两目标两决策变量多模态问题示意图 (左图和右图分别表示问题的决策空间和目标空间)Fig.1 Diagram of a two-objective two-decision-variable MMOP (the left figure and right figure are decision space and objective space respectively)

多目标进化算法 (Multi-objective evolutionary algorithms,MOEAs) 在求解非线性、决策类型多样、决策空间复杂的MOPs 上的有效性已经得到了广泛的验证[7-8].鉴于MOEAs 在MOPs 的标准测试问题和实际工程问题上的优异性能,多种MOEAs 被拓展以用于解决MMOPs.研究者将种群多样性保持机制与现有MOEAs 结合,以获得问题的全部最优解集,这类算法统称为多模态多目标进化算法 (Multimodal multi-objective evolutionary algorithms,MMEAs).但由于MMOPs 比传统的MOPs 具有更复杂的决策空间和映射关系,目前所提出的MMEAs 在求解MMOPs 时仍存在许多困难[9],例如,如何平衡决策空间的多样性和目标空间的收敛性,如何保留目标向量相似而决策向量相差较大的个体.

前期围绕MMOPs 的大部分工作是获得此类问题的多个全局最优解集,不考虑问题的局部最优解集.在火箭任务规划问题[6]中,对于相距较远的两个火箭发射窗口,其空间飞行时间和有效载荷相差非常小,因此对于决策者来说,获得这两个不同的解具有重要意义.最新的研究也指出,在现实问题中,存在多个全局最优Pareto 区域较为罕见.更普遍的情况是,多个全局最优与局部最优区域同时存在.从另一个角度来说,多个全局最优是存在局部最优的一种特殊情况,因此,同时获得问题的全局最优和局部最优区域更为重要[10].遗憾的是,针对此类问题的研究目前还比较少,仍处于初期阶段.为了进一步提升MMEAs 在具有局部最优解集的MMOPs 上的性能,本文进行了积极的探索,创新性体现在以下几个方面:

1) 提出了一种局部收敛性指标 (ILC).具体来说,区别于全局收敛性指标,局部收敛性指标只要求个体与它附近的个体进行对比.在进化过程中,基于局部收敛性指标可以保留问题的局部最优解.另外,该指标可以方便地嵌入到已有的MOEAs 中,从而使算法具有搜索问题局部最优Pareto 区域的能力.

2) 为了增强算法保持种群多样性的能力,提出了一种考虑目标空间和决策空间多样性的指标,并以此为依据,设计了一种能够同时获得问题的全局和局部Pareto 最优解的环境选择策略.

3) 结合局部收敛性指标和环境选择策略,提出了一种多模态多目标优化算法用以获得MMOPs的全局和局部Pareto 解集.通过对比其他代表性算法在测试问题上的表现,验证了所提算法的有效性.

本文内容安排如下:第1 节介绍多模态多目标优化的相关概念以及该类问题的求解难点;第2 节详细介绍本文所提的局部收敛性指标以及基于该指标的多模态多目标优化算法;第3 节通过实验对所提算法的有效性进行验证;第 4 节对本文研究进行总结,并提出未来可能的研究方向.

1 研究背景

1.1 多目标优化问题

现实世界中的许多工程应用问题,往往需要考虑多个优化目标.通常来说,不同的目标是互相制约的,只能通过权衡来获得令决策者满意的解.不失一般性,MOPs[11-12]可以表示如下

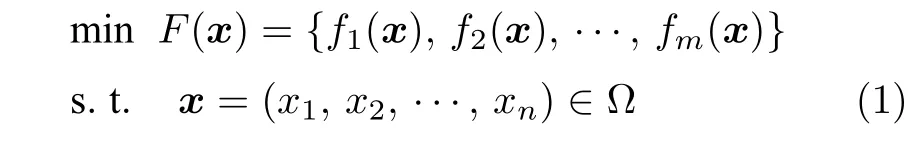
其中,Ω 为问题的可行域,fm(x) 为决策向量x的第m个目标函数值.与具有单个全局最优值的单目标优化问题不同,在多目标优化问题中,存在多个非支配解,称为Pareto 最优解集.解xA支配解xB当且仅当

一般来说,MOEAs 会给出一组互不支配的解集,称为Pareto 最优解集 (Pareto solution set,PS),并且不存在一个解能在所有目标函数上都优于其他解.而PS 在目标空间上的映射称为Pareto 最优前沿 (Pareto front,PF).

1.2 多模态多目标优化问题

多模态多目标优化问题可以定义[5,9]如下:

定义 1.如果一个多目标优化问题满足以下两个条件之一,则称该问题为多模态多目标优化问题.

1) 问题至少有一个局部Pareto 最优解集;

2) 问题至少有两个等效全局Pareto 最优解集,它们对应相同的PF.

定义 2.对于解集SL中的任意解x,如果不存在x的邻居解y,其中‖x-y‖≤δ,使得yPareto支配x,那么SL称为局部最优解集.

定义 3.对于解集SG中的任意解x,如果不存在解y,使得yPareto 支配x,那么SG称为全局最优解集.

从定义中可以看出,MMOPs 存在两种情况.情况1 可由图1 简单表示,即在决策空间中存在多个相距较远的PS 对应于相同的PF.换句话说,在目标空间Pareto 前沿上的一个目标向量,可以在决策空间上找到距离较远的多个最优解.情况2 可由图2 表示,其中B点对应目标空间中的P1点,A点对应局部PF 上的P2点.在情况1 的基础上,问题还存在一个或多个局部PF.

图2 具有局部帕累托前沿的两目标多模态问题 (左图和右图分别表示问题的决策空间和目标空间)Fig.2 A two-objective MMOP with local Pareto front (the left figure and right figure are decision space and objective space respectively)

由上述定义可知,对于MMOPs,只存在一个全局PF,而局部PF 可能有多个,且全局PF和局部PF 对应至少一个PS.图3 展示了MMF12 问题和MMF15 问题的PF和PS.从中可以直观地看到,MMF12 存在一个全局PF 对应于4 个等效全局PS,一个局部PF 对应于4 个等效局部PS;而MMF15则只有一个全局PS和一个局部PS.

图3 MMF12 (左)和MMF15 (右)问题的PF和PS 示意图Fig.3 Diagram of PF and PS for MMF12 (left) and MMF15 (right)

传统的MOEAs 的目标是获得一组靠近Pareto最优前沿的均匀分布的解集.这一目标包含两个重点:1) 解集具有良好的收敛性,其目标向量接近于Pareto 前沿;2) 解集在Pareto 前沿上均匀分布.为了达成这一目标,NSGA-II 算法先后使用了两个评价指标,即快速非支配排序和目标空间的拥挤距离.类似于NSGA-II,其他MOEAs 总是以收敛性为第一准则,辅以目标空间的均匀性选择策略,从而获得性能较好的解集.以图1 为例,在利用MOEAs求解MMOPs 问题时,假设算法已经通过搜索获得解A(对应于目标空间的点P),在新的迭代搜索中,算法得到解B′(对应于目标空间的点P′).那么,对于传统的MOEAs 来说,P与P′在目标空间将变得 “拥挤”.由于目标空间均匀性指标的存在,P′将不会在迭代过程中得到保留,因此算法难以同时获得解A和解B.即传统以收敛性为第一准则的算法难以求解多模态多目标优化问题.另外,对于存在多个局部PF 的MMOPs 来说,由于MOEAs以收敛性作为第一准则,在没有其他种群多样性策略的辅助下,算法将迅速收敛到问题的全局PF,因此不会保留该问题的局部PF.

为了获得MMOPs 的全部最优解集,近年来学者们提出了许多MMEAs.Omni-optimizer[13]可能是最具代表性的MMEA,它基于NSGA-II[14]引入了保持决策空间解的多样性的策略,包括基于拉丁超立方体采样的种群初始化方法、限制交配选择策略和替代拥挤距离.其中,替代拥挤距离旨在评估目标空间和决策空间中解的多样性.受此启发,基于niching 的协方差矩阵自适应 (Covariance matrix adaptation,CMA) 方法[15]在目标和决策空间中引入了聚合距离度量,可以将解集划分为多个niches.另外,双niches 进化算法 (Double-niched evolutionary algorithm,DNEA)[16]和基于决策空间的niching NSGA-II (Decision space-based niching NSGA-II,DN-NSGAII)[17]是两种基于Omnioptimizer 的增强算法,经实验证明,这两个算法在MMF 测试问题上表现优异.与传统采用模拟二元交叉算子 (Simulated binary crossover,SBX) 不同,MO_PSO_MM[18]和MO_Ring_PSO_SCD[19]使用粒子群优化 (Particle swarm optimization,PSO) 算子[20]来生成新的解并在传统MMOPs 上获得了良好的性能.此外,差分进化 (Differential evolution,DE) 算子[21]也被用来促进决策空间的多样性,例如MMODE[22]、DE-RLFR[23]等.然而,前期的工作为了更直观地展示算法获得不同PS 的能力,测试问题的决策变量通常被设计为2～3 个,并且问题的搜索难度较小,通常能够在10～50 代内找到最优解.

最近,Liu 等[24]考虑到现有的测试问题中,搜索不同PS 时难度一样,而在现实问题中,获得不同区域的解集难度往往是不同的.基于此,作者提出了一种新的测试问题集IDMP (Imbalanced distance minimization benchmark problems).这个测试集的主要特点是,搜索不同的区域需要的解的评价次数不同.经过实验,已有的算法在这类问题上表现较差,往往只能找到一个Pareto 解集.因此,该测试问题能够更加准确地衡量算法保持多样性和搜索不同PS 的能力.为了解决这类问题,Liu 等提出了一种基于距离的收敛性惩罚方法,并选择每次只更新一个解的steady 策略对种群进行更新,形成了CPDEA 算法.受基于指标的进化算法 (Indicatorbased evolutionary algorithm,IBEA) 启发,Li 等[25]提出了一种加权指标,可以衡量个体的局部收敛性.Fan 等提出了一种自适应分区搜索 (Zoning search with adaptive resource allocating,ZS-ARA)[26]策略,将整个搜索空间分成几个子区域进行搜索,从而提高算法保持多样性的能力.经过验证,这些算法在IDMP 问题上表现良好.

总体来说,MMEAs 的有效性得到了广泛的实验验证,但是目前的MMEAs 更多地关注于找到MMOPs 的全局最优解.在现实问题中,存在多个等效全局最优Pareto 区域往往是比较少的情况,更普遍的情况是,全局最优与局部最优同时存在.因此研究同时获得问题的全局最优和局部最优区域更为重要.遗憾的是,针对此类问题的研究目前还比较少.其中,PQ,ϵ-MOEA[6]是专门针对空间任务设计问题而设计的算法,其使用ϵ-dominance[27]进行后代选择;MMOPIO[28]基于Pareto 支配关系设计,能在一定程度上获得局部最优解;eMOEA/D-ADA[29]是基于分解方法的算法,通过给不同参考向量分配多个个体,也具有一定的局部最优搜索和保留能力;DIOP[30]则给出一种多样性的指标,并使用基于集合的多目标优化算法框架对问题进行求解,能够获得问题的局部最优解集;DNEA-L[10]则通过使用一种多前沿档案集更新方法来获取局部PS.但是,由于没有系统地讨论这类问题,因此在性能上仍有提升的空间.

Liang 等[31]提出了具有局部PF 的MMOPs 测试问题,并举办了相关的竞赛.在这之后,Lin 等[32]提出了使用基于DBSCAN 的双重聚类的方法来维持种群的多样性,能够获得问题的局部最优解集.然而,由于基于密度的聚类方法在对不同的解集区域进行聚类时存在误差,因此容易出现性能不稳定的情况.Li 等[33]则提出了一种基于分层选择的多目标优化算法 (Hierarchy ranking method based evolutionary algorithm,HREA) 来获取问题的全局和局部Pareto 解集.Tanabe 等[9]和岳彩通等[5]针对多模态多目标优化进行了较为详细的综述总结,总的来说,虽然获取MMOPs 的全局和局部最优解具有重要意义,但是相关的算法设计仍然处于起步阶段,设计一种鲁棒性高、性能好的考虑局部PS 的MMEA 成为MMOPs 研究领域的前沿问题.

2 基于局部收敛性指标的多模态多目标优化

2.1 局部收敛性指标

传统的MOEAs 更多地关注解集的收敛性,因此绝大多数算法都选择收敛性作为第一准则进行后代个体的选择[14].基于传统MOEAs 设计的多模态多目标优化算法考虑了决策空间的多样性,因此能够获得更多的等效PS.然而,传统算法往往只关注获得全局PS,从而舍弃局部PS 的搜索.为了加强算法对局部PS 的搜索能力,参考SPEA2 算法[34]中所提的元适应度值,本文提出一种局部收敛性指标,对于解xi,其局部收敛性指标计算如下

图4 为本文所提的局部收敛性指标计算示意图.与SPEA2 算法所提的元适应度值需要跟种群中所有的个体进行比较不同,在局部收敛性指标的计算中,个体只跟自己的邻居解进行比较,从而提高局部最优解的收敛能力.具体来说,对于决策空间中的解A来说,其处于局部PS (圆圈区域)中.在传统的MOEAs 中,由于全局PS (C点所在线条)的收敛性更好,因此解A和解B被解C支配,在进化过程中不会被保留.在局部收敛性指标的计算中,解A在计算支配关系时,只跟自身的邻居解(在当前示意图中,邻居只有解B) 进行比较,此时解A属于非支配解,能够保留并顺利进入下一次的进化.局部收敛性指标的计算中使用了邻居的概念,而决策空间中邻居解的定义是偏主观的,需要引入参数[4].不失一般性,在本文中,称两个解xi和xj为邻居,当且仅当它们的欧几里得距离小于V,计算如下

图4 局部收敛性指标示意图Fig.4 Diagram of local convergence indicator

其中,D表示决策变量的个数;分别代表第d个决策变量的最大值和最小值.

2.2 算法框架

前面具体介绍了局部收敛性指标的思想以及计算过程,基于该指标,本文提出了一种基于局部收敛性指标的多模态多目标优化算法 (MMEA based on local convergence indicator,ILC-MMEA).ILC-MMEA 的算法框架由算法1 表示.与大多数MOEAs一样,ILC-MMEA 由以下步骤组成:种群初始化,交配选择,后代生成,环境选择.本文引入了局部收敛性指标来搜索全局和局部的PS.并且在挑选父代个体时 (步骤 3)),使用了局部收敛性指标作为二元竞争的准则,从而加快算法的收敛速度和提升局部探索能力.具体来说,首先从当前种群Pop里随机挑选两个解并比较它们的局部收敛性指标值,较好的个体将被选择;如果它们的局部收敛性指标值一致,则拥挤距离小的个体被选择;这一过程将被重复执行,直到挑选出N个个体.之后,被挑选的父代个体将使用SBX和多项式变异 (Polynomial mutation,PM) 产生后代个体 (步骤 4)).另外,针对局部PS 的搜索问题,本文设计了一种新的环境选择策略.

算法 1.ILC-MMEA 算法框架

2.3 环境选择策略

在这一节中,将详细讨论基于ILC的环境选择策略,其基本思路由算法2 表示.

算法2.环境选择策略

首先,将种群与新生成的后代个体进行合并,并计算合并后种群的局部收敛性指标ILC(步骤 1)、步骤 2)).根据式 (3),当=0 时,表明解xi不被它的任何邻居解支配.因此本文设计了一种二次选择策略,具体为:当局部非支配解的个数小于种群大小N时,按照ILC的值对种群进行排序,随后选择前N个个体进入下一代 (步骤 4));否则,算法将首先挑选出局部非支配解,然后计算它们的拥挤距离,随后删除拥挤距离较大的解,从而保持新种群的大小为N(步骤 5)、步骤 6)).

ILC-MMEA 使用拥挤距离作为第二准则对种群中的个体进行挑选.一般来说,传统的MOEAs更多地关注目标空间中解集分布的均匀性,而MMEAs 则更多地关注决策空间的均匀性[5,9],这一点可以通过图5 对目标空间和决策空间的分布性进行说明.图5 中左边表示解在决策空间的分布性很好,但是在目标空间的分布性较差,对应于传统的MMEAs;图5 中间表示解在决策空间的分布性很差,但是在目标空间的分布性很好,对应于传统的MOEAs;理想状态的解分布应该如图5 中右边所示,即解在决策空间和目标空间的分布性都很好.为了实现这一目标,本文提出了一种改进的种群拥挤距离计算方法,具体如下

图5 目标空间和决策空间的分布均匀性Fig.5 Distribution uniformity in the objective space and the decision space

其中,‖xj -xi‖表示xi和xj的欧氏距离,f(xi) 则代表解xi对应的目标向量归一化之后的值.值得注意的是,在计算之前,需要对xi和xj的值进行归一化.

新提出的拥挤距离充分考虑了解集在目标空间和决策空间的相对位置,因此可以获得在两个空间中分布更加均匀的解集.另外,为了更好地平衡两个空间的差异,算法对两个空间的向量使用了统一的归一化策略.

2.4 算法计算复杂度分析

本节将讨论ILC-MMEA 在最坏情况下的计算运行时间复杂度.对于每一代,主要执行三个步骤:交配选择,个体交叉变异,环境选择.假设种群大小、问题的目标数量和决策变量的数量分别为N,M,D.对于每一代,交配选择需要 O (MN2) 的时间复杂度.采用SBX 来执行交叉操作,需要的运行时间为 O (DN). 另外,对于环境选择,算法需要计算ILC,其时间复杂度为 O (MN2/2);而二次选择的时间复杂度为 O (D2);因此环境选择的总复杂度为max{O(MN2/2),O(D2)}. 那么,ILC-MMEA 算法的最终时间复杂度为 m ax{O(GMN2/2),O(GD2)},其中G表示迭代次数.通常有N＞D,因此,可以确定ILC-MMEA 的运行时间复杂度为 O (GMN2).作为比较,Two_Arch2、IBEA和NSGA-III 的运行时间复杂度分别为 m ax{O(),O(MN2)},O(N2),O(MN2)}[35].从理论分析来看,ILC-MMEA 的计算效率很高.此外,在后续实验部分,算法的运行时间将与其他代表性MMEAs 进行比较.

3 实验

3.1 实验设置

3.1.1 测试问题和对比算法

为了测试ILC-MMEA 在求解传统MMOPs和具有局部PS 的MMOPs 时的性能,本节将使用IDMP 测试集[24]和IEEE CEC 2019 MMOP 测试集[31].相比于其他的MMOPs 测试集,IDMP 测试集在搜索不同的PS 时搜索难度不同,在某种程度上来说,此类问题更能显示出算法保持种群多样性的能力;另外,IEEE CEC 2019 MMOP 测试集中的部分测试问题 (MMF10～MMF13,MMF15) 具有局部PS,因此被选择用来测试所提算法获得局部PS 的能力.

为了验证ILC-MMEA 在解决MMOPs 中的有效性,本文选择Omni-optimizer[13]、DN-NSGAII[16]、MO_Ring_PSO_SCD[19]、MMEA-WI[25]、CPDEA[24]、DNEA-L[10]和MMOEA/DC[32]作为对比算法.具体来说,Omni-optimizer、DN-NSGAII和MO_Ring_PSO_SCD 都是求解MMOPs 的代表性算法,其性能已经得到了广泛验证;MMEAWI和CPDEA 是专门为解决不平衡MMOPs 提出的算法;DNEA-L和MMOEA/DC 则是最新关注于获得全局和局部PS 的算法.

为了保证对比的公平性,对于所有算法,设置种群大小N=100D,函数评估的最大次数设置为NF E=5 000D,其中D是决策变量的数量.此外,除了MO_Ring_PSO_SCD 采用PSO 算子,其他算法均使用SBX和PM 算子用于生成后代,其中交叉概率和变异概率分别为1和 1 /D,ηc=ηm=20.对比算法中的具体参数均按照原论文设置.所有实验均基于PlatEMO v1.6[36],计算机配置为Intel i9-9900X @ 3.50 GHz,64 GB RAM.为方便多模态多目标相关领域研究人员的后续研究工作,本文开放了ILC-MMEA 的源代码,相关代码可从以下网站获取:https://gitee.com/wenhua-li/ilcmmea.

3.1.2 性能评价指标

针对MOEAs 性能的评价指标包括超体积 (Hypervolume,HV)[37]、世代距离 (Generation distance,GD)[38]和反世代距离 (Inverted generation distance,IGD)[38]等.它们中的大多数是用来衡量解集在目标空间中接近真实Pareto 前沿的程度和解集分布的均匀程度.由于MMEAs 旨在获得所有PS,因此还应衡量解集在决策空间中的性能.因此,在本文中采用IGDX[39]作为评价指标,以评价获得的解集与真实PF和真实PS 的近似程度.对于一个解集X,IGDX 的计算过程可以表示如下

其中,ED(x,y) 表示解x和解y的欧氏距离,X*代表真实Pareto 集合中的均匀采样,|X*|表示集合X*中解的总个数.IGDX 的值越小,表示解集的收敛性和均匀性越好,当IGDX 值为0 时,表示获得的解集能完全覆盖参考解集.

3.2 传统MMEAs 性能对比

为了测试ILC-MMEA 在求解传统MMOPs 时的性能,本文使用了IDMP 测试集.具体来说,相比较前期提出的MMOPs 测试问题,获得IDMP 测试问题的全部Pareto 最优解集更加困难,因此更能够体现出MMEAs 保持种群多样性和获取不同PS的能力.表1 列出了所有算法31 次独立运行的IGDX 的平均值和方差.另外,本文使用Wilcoxon 秩和检验来比较ILC-MMEA 与每个对比算法的性能差异,其中显著性水平p设置为0.05.在表1 的最后一列中,符号 “+”和 “–” 表示当前算法与ILC-MMEA 相比,能获得更好和更差的性能的测试问题数量.此外,符号 “=” 表示该对比算法与ILC-MMEA 之间没有显著差异的测试问题数量.

从表1 中可以观察到,ILC-MMEA 在所选测试问题上表现出比其他代表性算法更好的性能.具体来说,12 个测试问题中,ILC-MMEA 在8 个问题上表现出了最佳性能.此外,MMOEA/DC、MMEA-WI和CPDEA 分别在2 个、1 个和1 个测试问题上获得了最好的IGDX 值.从表1 中可以看出,ILC-MMEA、MMOEA/DC、MMEA-WI和CPDEA 相较于其他对比算法性能更强,其在IGDX指标值上有跨越量级的领先.这是因为,CPDEA和MMEA-WI 是专门为了解决IDMP 问题提出的,考虑了搜索不同PS 时的不平衡性问题;ILC-MMEA和MMOEA/DC 则是考虑到了决策空间中存在局部PS 的情况,因此在求解PS 不平衡问题时依然能够获得问题的全部PS.但是,随着目标个数的提升,只有ILC-MMEA和MMOEA/DC 能够获得较好的结果,其他算法均不能够获得问题的全部PS.虽然DN-NSGAII和Omni-optimizer 是为多模态多目标优化设计的,但似乎它们在所选基准问题上表现不佳.IDMP 测试问题在搜索不同PS 时存在不平衡,因此一般的MMEAs 很难获得所有PS.DN-NSGAII和Omni-optimizer 是MMOPs 早期研究中的两个代表性算法,其思想启发了众多针对MMOPs 的算法和相关工作,但是在IDMP 测试问题上表现较差.

表1 不同算法在IDMP 测试问题上31 次独立运行的IGDX 平均值和方差Table 1 Mean and variance of 31 independent runs of IGDX for different algorithms on IDMP test problems

图6 展示了所有算法在IDMPM3T4 问题上获得的PS和PF (挑选出每个算法最接近平均IGDX值的运行结果进行展示).从图中可以看出,ILC-MMEA和MMOEA/DC 能够获得所有的PS,而DNEA-L、CPDEA、MMEA-WI和MO_Ring_PSO_SCD 只能获得其中的部分PS;DN-NSGAII和Omni-optimizer 只能获得其中一个PS.另外,图7展示了所有算法在具有4 个决策变量的IDMPM4T3问题上获得的PS.可以看到,仅有考虑了局部PS的DNEA-L、ILC-MMEA和MMOEA/DC 能够获得全部的PS,并且ILC-MMEA和MMOEA/DC获得的解集分布均匀性明显更好.此外,可以明显地看到,ILC-MMEA和MMOEA/DC 最终获得的解集中包含了非支配解.这是因为这两个算法都考虑了获得问题的局部PS,因此还有少量的个体继续在决策空间进行探索.

图6 不同算法在IDMPM3T4 问题上获得的PS和PFFig.6 PS and PF obtained by different algorithms on IDMPM3T4 problem

图7 不同算法在IDMPM4T3 问题上获得的PS (蓝色实线)和真实PS (红色虚线)Fig.7 True PS (red dotted lines) and obtained PS (blue solid lines) by different algorithms on IDMPM4T3 problem

总体来说,在IDMP 测试问题上,ILC-MMEA、MMOEA/DC、MMEA-WI和CPDEA 表现良好,而随着目标个数和决策数量的增加,ILC-MMEA和MMOEA/DC 的性能优势更加凸显,且ILC-MMEA性能更佳.

3.3 考虑局部最优算法性能对比

本节展示了ILC-MMEA和对比算法在具有局部PS 的MMOPs 上的性能.具体来说,实验挑选了IEEE CEC 2019 MMOP 中的部分测试问题,包括MMF10、MMF11、MMF12、MMF13和MMF15.为了降低随机性带来的影响,所有实验均独立执行31 次.与上一节相同,使用Wilcoxon 秩和检验来表示不同算法相比于ILC-MMEA 的性能好坏.

表2 列出了所有对比算法在测试问题上获得的IGDX 的平均值和方差.从表中可以看出,在全部5 个测试问题中,ILC-MMEA 在4 个测试问题上表现出最好的性能,MMOEA/DC 在1 个测试问题上表现最好.DNEA-L、MMOEA/DC和ILC-MMEA 相比于其他算法表现更加出色 (IGDX 值更小).这是因为,这三个算法均采取了一定的策略对局部PS 进行搜索并保留.对于本节选择的测试问题,这三个算法都能找到并保留局部PS,因此其性能表现优异.

表2 不同算法在具有局部PS 测试问题上31 次独立运行的IGDX 平均值和方差Table 2 Mean and variance of 31 independent runs of IGDX for different algorithms on MMOPs with local PS

图8 直观地展示了所有算法在具有局部PS 问题上的表现.可以看到,MMOEA/DC和ILC-MMEA能够找到问题的全局和局部PS.DNEA-L 在MMF11问题上能够找到全局和局部PS,但是在MMF12上只能获得部分PS,且解集分布的均匀性较差.对于早期提出的MMEAs 而言,由于算法没有考虑局部PS 的搜索,因此无法对局部PS 进行保留.ILC-MMEA 获得的PF 分布性更加均匀.这是因为,ILC-MMEA 引入了全新的种群拥挤度计算方式,能够更好地平衡目标空间和决策空间分布的均匀性.在MMF12 问题上,MMOEA/DC 获得的PF相比于ILC-MMEA 更加均匀,而PS 情况则相反.由于篇幅限制,算法在其他问题上的PF和PS 没有全部画出,感兴趣的读者可以在论文代码开源地址获得所有数据结果.总体来说,ILC-MMEA和MMOEA/DC 均能够获取问题的全局和局部PS,DNEA-L 能够获取问题的部分局部PS,且ILC-MMEA 获得的解集分布性更好.

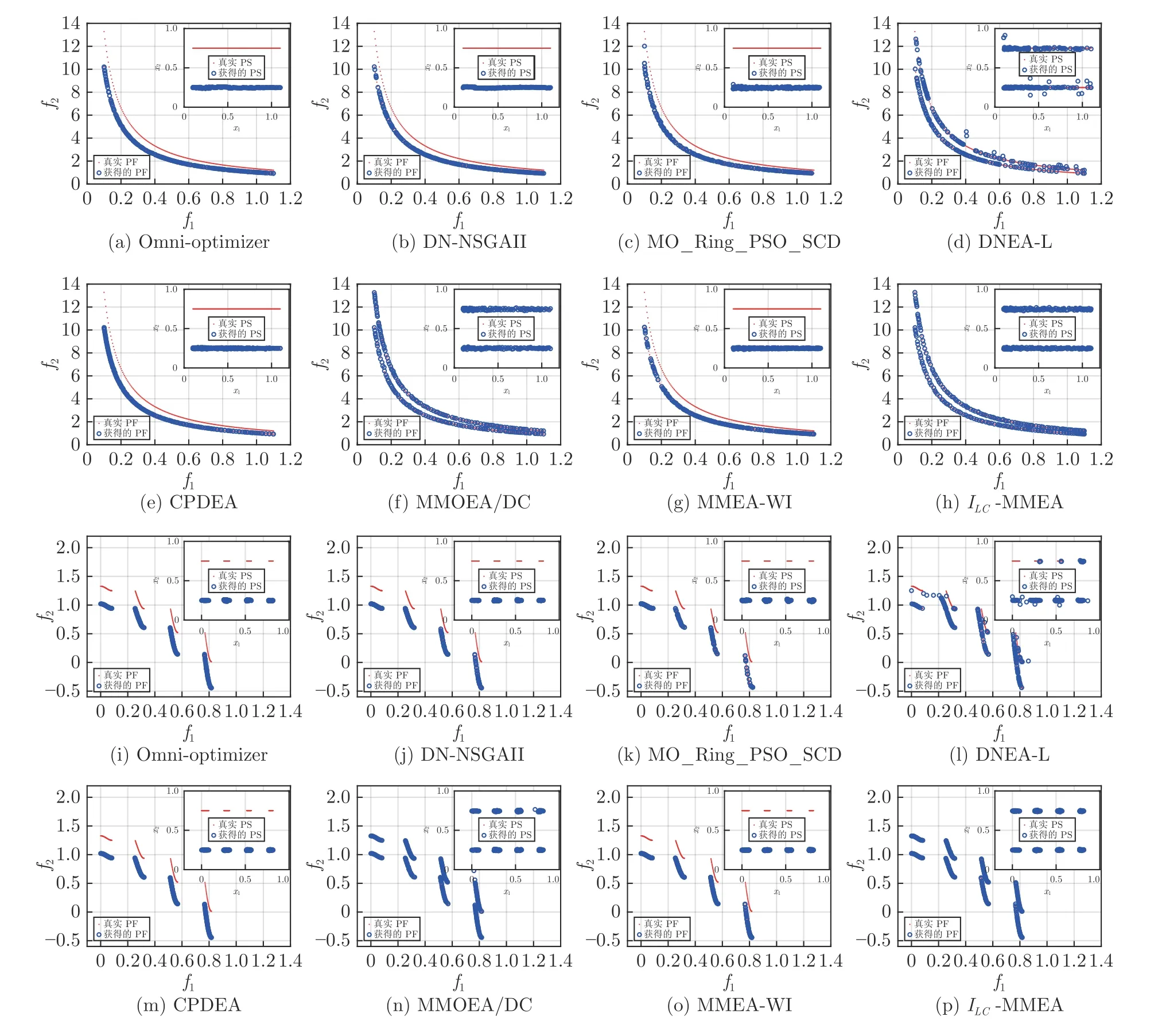
图8 不同算法在MMF11 问题 (前两行)和MMF12 问题 (后两行) 上获得的PS和PFFig.8 PS and PF obtained by different algorithms on MMF11 (first two rows) and MMF12 (last two rows) problems

3.4 算法运行时间对比

前文在理论上给出了ILC-MMEA 算法的计算时间复杂度,为了更加直观地展示不同MMEAs 算法的计算耗时,本节将使用实验的方法对时间复杂度进行分析.具体来说,将使用Multi-polygon 作为基准测试问题.该测试问题可以方便地扩展到高维,因此,设置目标函数个数M分别为3、4、8、10,D=4 ,并统一使用N=200 ,NF E=20 000 进行31 次独立实验,取结果的平均值进行比较.

图9 展示了不同算法在目标个数不同的测试问题上的计算时间.可以看到,MMOEA/DC、MMEAWI和ILC-MMEA 的计算复杂度随着目标个数的提升并没有明显的增大.对于DN-NSGAII和Omni-optimizer 来说,求解目标个数为4 时的优化问题所用时间甚至小于目标个数为3 时的求解时间.进一步分析可以知道,这两个算法的计算复杂度与当前种群中非支配解占比息息相关.当目标个数增大时,算法运行前期种群中非支配解的占比较低,这导致了计算时间的下降.另外,CPDEA、DNEA-L和MO_Ring_PSO_SCD 的计算时间随着目标个数的增大有微小增加.总体来说,ILC-MMEA 的计算时间在所有对比算法中处于中间位置,具备较好的计算效率.

图9 不同算法在不同目标个数测试问题上的计算时间Fig.9 Computational time of different algorithms on test problems with different number of objectives

4 结论

获得MMOPs 的全部PS 对于决策者具有重要意义.然而,由于目标空间多样性与决策空间多样性存在一定的冲突,因此,获得全部PS 仍然是进化计算领域面临的一个巨大挑战.此外,搜索并保留决策者能接受的局部最优PS 可以认为是保留全部全局PS 的更普遍情况.这是因为,拥有多个全局最优PS 的问题是具有局部最优PS 的一个特例.研究具备搜索局部PS 能力的算法可以更好地解决MMOPs.在本文中,提出了局部收敛性指标和基于双空间的拥挤距离,并通过实验验证了所提方法的有效性,说明关注问题的局部PS 可以更好地解决MMOPs.

目前,针对MMOPs 的研究大多聚焦在连续型优化上[5,9],且问题的决策空间较小 (决策变量个数较少),已有算法重点考虑了解集的分布性而没有重视算法的搜索能力.然而实际问题的决策变量可能是多类型或大规模的.近期,CEC 会议举办了针对路径规划的多模态多目标竞赛[40-41],公开了一系列测试集,研究了多模态多目标优化算法在离散型问题上的性能,取得了较多的关注.另一方面,针对多模态多目标优化算法的实际应用还比较少.这是因为,决策者难以确定待优化问题是否属于多模态优化问题;并且,已有的MMEAs 在实际问题上的效果还有待检验.因此决策者更倾向于选择传统的MOEAs 对问题进行求解,这对理解问题的决策空间属性造成了一定的障碍.因此,如何快速表征某个问题是否为多模态多目标优化问题是推广此类算法的关键.另外,未来的研究方向将聚焦于提升多模态多目标优化算法在大规模决策变量问题上的性能以及推动多模态多目标优化算法的实际应用.