基于流模型的缺失数据生成方法在剩余寿命预测中的应用

张博玮 郑建飞 胡昌华 裴 洪 董 青

对于锂电池、轴承、航空发动机和陀螺仪等复杂关键设备,由于受到内部应力或外界环境的影响,其设备的健康状态会不可避免的出现退化,最终引发设备及所在系统的失效,甚至导致人员和财产的损失[1-2].为切实掌握设备的健康性能,保障设备安全可靠运行,预测与健康管理 (Prognostics and health management,PHM) 技术[3-4]近年来受到了广泛关注.作为PHM 技术的关键环节,剩余寿命(Remaining useful life,RUL) 预测旨在通过分析状态监测收集的退化数据,来预测设备的剩余寿命.随着先进传感、物联网技术的进步和监测工艺的发展,当代设备复杂化、自动化以及智能化水平不断提升,推动数据驱动的剩余寿命预测技术进入了 “大数据”时代.

在工程实际中,由于机器故障 (如测量传感器故障) 或人为因素 (如未记录) 不可避免地导致部分数据缺失[5-7].若利用这类不完整数据预测设备剩余寿命,将面临难以准确描述设备退化规律的现实问题,进而将影响设备的健康管理和维修决策.因此,针对缺失数据统计特性的多样性随机退化设备剩余寿命预测问题得到了大量学者的关注.

随着深度神经网络在计算机视觉、密度估计、自然语言和语音识别等领域的兴起[8],深度生成模型[9]开始应用于时间序列的生成,其基本思路是通过捕捉时间序列的分布特征,对时序数据进行再生成,从而填补数据.Yoon 等[10]首次提出了一种基于生成式对抗网络 (Generative adversarial network,GAN) 框架的缺失数据输入方法获得了较好的填充效果.张晟斐等[11]基于柯尔莫可洛夫—斯米洛夫检验 (Kolmogorov-Smirnov test,K-S test) 检验的思想,改进卷积生成对抗网络 (Deep convolutional generative adversarial network,DCGAN),获得了更高精度的生成结果,但是存在生成器和判别器模式崩溃、难以训练的风险.Nazabal 等[12]融合基本的变分自编码器 (Variational autoencoder,VAE)和高斯过程,利用变分推断在多维时间序列填充问题上得到了更理想效果.在基于深度学习的框架下,现有研究集中在GAN和VAE 的改进和优化方面.根据处理极大似然函数方法的不同,GAN 采用网络对抗和训练交替的方式,避免优化似然函数,虽然生成精度高但是训练过程困难,VAE 采用似然函数的变分下界代替真实的数据分布,只能得到真实数据的近似分布.因此,亟需研究一种既能保证模型精度又容易训练的深度生成模型.

近年来,为了克服模型精度和训练速度方面的局限性,可逆网络构造似然函数的流模型 (Flowbased model,Flow) 及改进模型[13-16]被应用于图像、音频生成领域效果显著.其中,非线性独立成分估计(Non-linear independent component estimation,NICE) 是首个基于Flow 模型的变体[13].针对完整的一维时序数据生成问题,Ge 等[17]提出了一种基于NICE 框架的生成网络来模拟配电网络的一维日常负载曲线.相比于GAN 与VAE,NICE 的生成效果能够更好地捕捉日常负载曲线的时空相关性.薛阳等[18]提出了基于NICE 框架的生成网络来增强分布式光伏窃电数据曲线,通过对比GAN 与VAE的生成效果,NICE 具有准确的似然估计,生成的样本更接近真实数据曲线.尽管NICE 面向完整时序数据时表现出良好的生成效果,但应用于缺失时序数据情形下的数据生成则鲜见报道.因此,如何利用NICE 挖掘出缺失数据的演变规律,以克服传统GAN和VAE 所面临的模型精度较低以及训练速度过慢的难题,是有待进一步研究的重要问题.同时,训练过程中如何优化NICE 模型参数是影响生成效果的关键因素,需予以重点考虑.

本文依靠NICE 网络的生成优势,提出了一种改进NICE 网络的缺失数据生成方法.该方法充分利用NICE 强大的分布学习能力,通过粒子群优化(Particle swarm optimization,PSO) 算法,将生成序列与真实序列之间的分布偏差融入NICE 采样生成样本的退火参数中,在提升训练速度的同时保证生成序列与真实序列的一致性.在此基础上,本文利用融合注意力机制的双向长短期记忆网络 (Bidirectional long short term memory with attention,Bi-LSTM-Att),建立了设备退化趋势预测模型进行剩余寿命预测.最后,通过锂电池的退化数据,对所提方法生成数据和预测数据的可靠性进行实例验证.

1 基于PSO-NICE 的数据生成

1.1 流模型

流模型的基本思路是:复杂数据分布一定可以由一系列的转换函数映射为简单数据分布,如果这些转换函数是可逆的并且容易求得,那么简单分布和可逆转换函数的逆函数便构成一个深度生成模型.

具体地,流模型假设原始数据分布为PX(x),先验隐变量分布为PZ(z) (一般为标准正态分布),可逆转换函数为f(x) (z=f(x)),生成转换函数为g(x)(g(x)=f-1(x)),基于概率分布密度函数的变量代换法可得:

其中,D是原始数据的维度,是可逆转换函数f(x) 在x处的雅可比行列式 (Jacobian),而更高维度的监测数据会增加Jacobian 的计算复杂度,导致模型拟合的负担多于求解可逆函数的反函数的过程.因此,流模型除了转换函数f(x) 可逆易求外,还需确保其Jacobian 易于计算.基于最大对数似然原理,流模型的训练优化目标为:

当流模型训练过程结束时,通过采样概率分布Z～PZ(z)得到随机数,其中采样分布一般为标准正态分布,然后通过可逆转换函数的反函数g(z)=f-1(z)生成新的数据分布.从生成模型的出发点来看,流模型可以提供精确的估计,能够生成高质量的样本.

NICE 是首个基于流模型的无监督深度神经网络生成模型[13].其优势在于能够得到精确的对数似然估计,易于训练,且基于可逆操作无需单独构建生成网络,它与训练网络共享同一套参数,最后从标准正态分布中采样随机数来生成样本.然而,实际上对于训练好的NICE 模型,采样标准差并不一定是1,因为更小的方差可以通过牺牲样本多样性增加样本真实性,所以理想的采样标准差一般比1稍小.最终采样的正态分布标准差,被称为退火参数[19].因此,当NICE 深度生成模型处理时间序列样本时,选择合适的退火参数是决定生成样本精度高的关键性因素.

1.2 PSO-NICE 模型

为了降低NICE 模型生成分布与原始分布的偏差,利用粒子群优化 (PSO) 算法快速迭代找到退火参数全局最优解,从而改进NICE 反向生成模型.

具体地,PSO-NICE 网络结构如图1 所示.NICE 由多个分块加性耦合层 (交错混合方式)和一个尺度压缩层组成,每一个分块加性耦合层模拟一个可逆变换函数f(x),通过交错混合来连接两个相邻的分块加性耦合层.如图1 所示,按照向右箭头的方向为正向训练过程,向左箭头的方向为反向生成过程.NICE 作为一类无监督向量变换模型,能够确保将输入数据的分布转化为标准正态分布,在反向生成时,从标准正态分布中采样随机数来生成样本,采用PSO 来对退火参数进行优化,提升NICE模型的反向生成能力.

以图1 为例,分别介绍分块加性耦合层、交错混合和尺度压缩层的结构和参数.

图1 PSO-NICE 网络框架图Fig.1 PSO-NICE network frame diagram

NICE 通过分块加性耦合层来拟合可逆变换函数f(x). 具体地,将维度为D的原始数据输入样本划分为两部分x1和x2,不失一般性,将x的各个维度打乱后重新排列,选取x1=x1:d为前d维元素组成的向量,x2=xd+1:D为后 (D-d) 维元素组成的向量,并作如下变换:

其中,Id和Id+1:D分别表示d维单位矩阵和(D-d)维单位矩阵,根据分块矩阵的结构,由式 (5) 可以得到J(f(x)) 是一个下三角矩阵形式,并且对角线元素全部为1.分块加性耦合层巧妙的设计不仅使得变换函数的逆函数易于求解,而且它的Jacobian 结果固定为1.

NICE 通过交叉耦合来连接两个相邻的分块加性耦合层,将分块加性耦合层1 输出的两部分直接交换作为分块加性耦合层2 的输入:

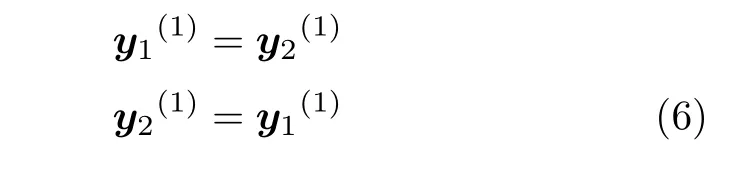
由式 (6) 知,分块加性耦合层的耦合操作只作用在第二部分,第一部分是恒等的变换.交错混合的操作简单,即前一个分块加性耦合层等价变换的向量可以在下一个分块加性耦合层进行非等价变换,可使信息充分融合.

其中,s各元素是要训练优化的非负参数向量,可识别维度的重要程度 (其大小决定了维度的重要程度),起到压缩流形的作用.代入上一节流模型的优化目标式 (2),NICE 模型的训练优化目标为:

上述优化目标即为NICE 模型训练的损失函数,经过堆叠多个分块加性耦合层和一个尺度压缩层,在流模型的框架下,降低了可逆函数的反函数和Jacobian 的计算复杂度,NICE 完成了网络构建.

在NICE 网络基础上,PSO 首先初始化一群随机粒子 (随机解),每个粒子的维度与原始样本保持一致,退火参数初始化为1,然后通过迭代找到最优解.在每一次的迭代中,粒子通过跟踪两个 “极值”(个体最优值pbest,群体最优值gbest) 实现更新.PSO 的标准形式如下:

其中,i=1,2,···,N,N是粒子群中粒子的总数,vi是粒子的速度,rand() 是介于 ( 0,1) 之间的随机数.vi是粒子当前的速度,xi是粒子当前的位置,c1和c2是学习因子,一般c1=c2.vi的最大值为vmax(通常大于0),如果vi大于vmax,则vi=vmax.

PSO 的优化目标选择生成分布与原始分布的推土机 (Earth-mover,EM) 距离,又称Wasserstein 距离.EM 距离相对KL 散度与JS 散度的优势在于平滑性更好,即使对两个分布很远几乎无重叠的情况,仍能反映两个分布的远近.该优点可保证PSO 迭代过程的初始阶段能够快速收敛.EM 距离越小,表明生成分布与原始分布越接近.EM 距离可表示为:

其中,Π (P1,P2) 是P1和P2分布组合起来的所有可能的联合分布的集合.对于每一种可能的联合分布γ,可从中采样 (x,y)～γ得到一个样本x和y,并计算出该对样本的距离‖x-y‖,进而可计算该联合分布γ下,样本对距离的期望值 E(x,y)-γ[‖x-y‖].在所有可能的联合分布中能够对这个期望值取到的下界即为EM 距离.

综上,在NICE 反向生成过程引入PSO,优化采样分布的退火参数,可以充分利用流模型的可逆生成模型,增加对生成结果的反馈,提升网络模型的生成效果.

2 基于Attention 的Bi-LSTM 的RUL预测

双向长短期记忆网络 (Bi-LSTM) 通过堆叠前向LSTM 层和后向LSTM 层,来提取序列的深度特征.与单个LSTM 层相比,能够充分利用监测数据过去与未来的潜在信息.反映设备退化信息的长时间序列在输入Bi-LSTM 网络时会通过滑动时间窗处理划分为时间步Xi对应的短序列,而不同时间步的短序列所蕴含的设备退化特征往往不同.

为了捕捉对预测结果贡献度较高的特征,引入注意力机制 (Attention) 层,将对预测结果贡献度高的特征赋予更高的权重,贡献度低的特征赋予较低的权重,对Bi-LSTM 的提取后的特征进行再次融合.

具体地,融合注意力机制的双向长短期记忆网络Bi-LSTM-Att 结构如图2 所示,X1,X2,X3,···,Xn为一组输入随机退化的监测数据经过滑动时间窗处理后的短时间序列,前向LSTM 层和后向LSTM 层对输入的短时间序列进行前向和后向的特征提取得到隐藏状态yi=[y1,y2,y3,···,yn],Attention 层对提取的特征分配不同的权重ai=[a1,a2,a3,···,an],最后连接一个全连接层,得到预测结果y.Attention 层的计算过程如下:

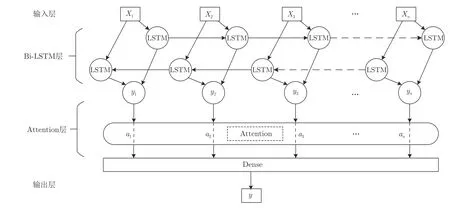
图2 Bi-LSTM-Att 网络框架图Fig.2 Bi-LSTM-Att network frame diagram

其中,t anh(·) 为非线性激活函数,其范围为 (-1,1),Wi和bi分别为隐藏状态yi=[y1,y2,y3,···,yn] 的权值矩阵和偏置矩阵,ai为Attention 层分给不同隐藏状态的权重,y为对所有隐藏状态加权求和后得到的综合特征.

综上,在Bi-LSTM 层后引入Attention 层,对不同的退化特征有不同的侧重,可以充分利用每个时间步的隐藏状态,提取有用信息,提升网络模型的预测效果.

3 基于PSO-NICE 缺失数据生成的RUL预测

基于PSO-NICE和Bi-LSTM-Att 的监测缺失数据生成和RUL 预测方法流程如图3 所示,具体的步骤为:

图3 缺失数据生成和RUL 预测流程图Fig.3 Missing data generation and RUL prediction flowchart

1) 样本各维度归一化:为了后期深度学习模型能够高效训练、挖掘深层次特征,需要对训练的原始数据进行必要的预处理操作,将含有缺失数据的监测原始退化监测数据每个样本的各个维度分别线性归一化到 ( 0,1) 区间,得到PSO-NICE 模型的训练样本,反归一化是归一化的逆操作,归一化与反归一化公式如下:

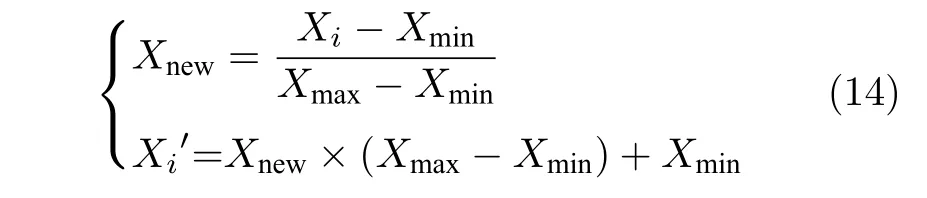
其中,Xmax和Xmin为某个维度样本的极值 (最大值和最小值),i为样本个数.

2) 搭建NICE 网络模型:根据样本量的大小,配置NICE 正向训练过程参数.将归一化后的训练样本作为模型的输入,进行深度无监督学习.

其中,NICE 网络结构模型参数主要是对分块加性耦合层的处理,包括分块加性耦合层的层数,耦合层的数量及其每一层的神经元数量.一般地,以4 个分块加性耦合层为基础建立模型,耦合层一般选择全连接层.随着输入数据分布的复杂度提高,由于交叉耦合的处理方式,分块加性耦合层的数量需要以偶数倍增加.同时,也可以加深耦合层的数量和增加每层神经元的数量来拟合复杂数据的分布.

3) 搭建PSO 迭代模型:引入一群与训练样本维度相同的粒子群,对NICE 反向生成过程模型的生成分布效果进行迭代优化,得到NICE 反向生成过程模型最优的退火参数.

其中,粒子的维度即为样本维度,粒子群的大小应不少于2,初始化的位置和最大速度可以根据优化目标的经验值设置参数,否则需要更多的迭代次数.最后,通过实验观察迭代效果,优化目标趋于稳定时停止训练,选择保证训练效果的最低迭代次数.

4) 缺失数据填补:选择最优退火参数下正态分布的随机数,作为NICE 反向生成过程模型的输入,将模型生成的全部样本反归一化到原始样本的变化区间,将与缺失数据的时间维度最接近的样本数据作为填补值,与原始数据一起组成完整的退化时间序列样本.

5) 构建Bi-LSTM-Att 预测模型:将填补后的数据与历史数据再次线性归一化,按照Bi-LSTM的输入格式,进行时间滑动窗口处理,作为Bi-LSTMAtt 的输入.训练调整Bi-LSTM-Att 预测模型的结构参数和训练参数,最后通过迭代预测得到RUL的预测值.

4 实验与分析

为了验证本文提出的基于PSO 改进NICE 的缺失数据生成方法和基于Attention 改进Bi-LSTM的RUL 预测方法,本文采用美国马里兰大学先进寿命周期工程中心 (Center for Advanced Life Cycle Engineering,Calce) 提供的CS2 类型电池容量退化数据集[6],共包含四块电池退化数据:CS2_35,CS2_36,CS2_37,CS2_38.这四组电池容量退化的完整曲线如图4 所示.

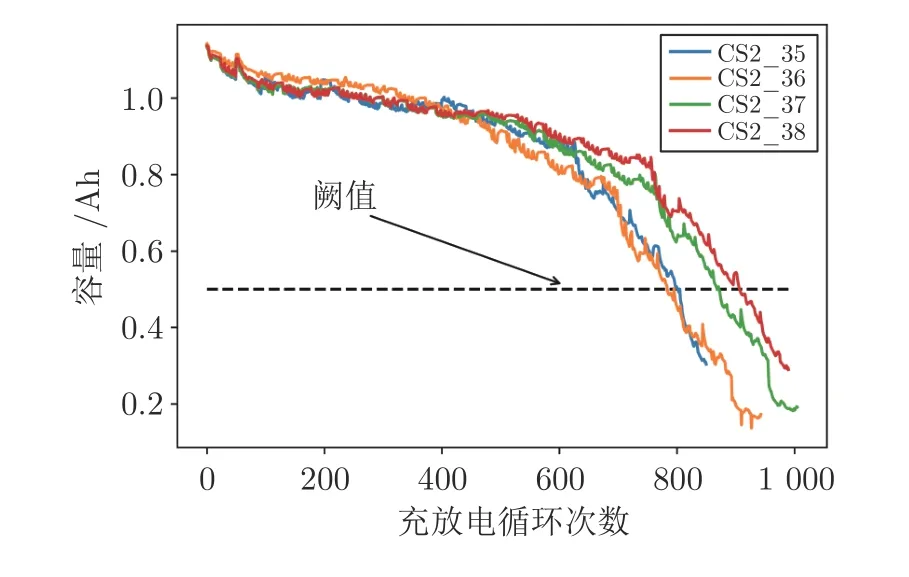
图4 CS2 电池组容量退化轨迹Fig.4 CS2 battery pack capacity degradation trajectory

图4 中,电池容量可以有效反映电池健康状况,实际应用中通常采用在一定充放电条件下电池容量衰减到失效阈值时所经历的充放电周期次数来描述电池的RUL,因此选择该指标进行锂电池RUL 预测.其中,失效阈值选择0.5 Ah.锂离子电池的RUL指从当前时刻开始至锂离子电池容量不能维持设备正常工作所经历的充放电周期次数.

为确保对比的公正性,本文采用文献[11] 中DCGAN-KS 模型的缺失数据设置模式.主要体现在缺失机制与缺失率两个方面,缺失机制设定为完全随机缺失 (Missing completely at random,MCAR),即数据的缺失概率与缺失变量以及非缺失变量均不相关[20].不同于MCAR,随机缺失 (Missing at random,MAR) 指的是数据的缺失不是完全随机的,即该类数据的缺失依赖于其他完全变量.在实际生产过程中,由于设备复杂和环境恶劣,大多缺失类型属于MCAR.不失个体差异性,生成数据实验以CS_37 电池为例.缺失率是在CS2_37数据的前850 个充放电循环基础上,分别选择10%、30%、50%和70% 四种模式.本文通过调用python 的random 库,选择缺失率分别为10%,30%,50%和70% 的sample 函数,用于产生生成模型的训练数据.由CS2_37 构造的原始数据和训练数据如表1 所示.

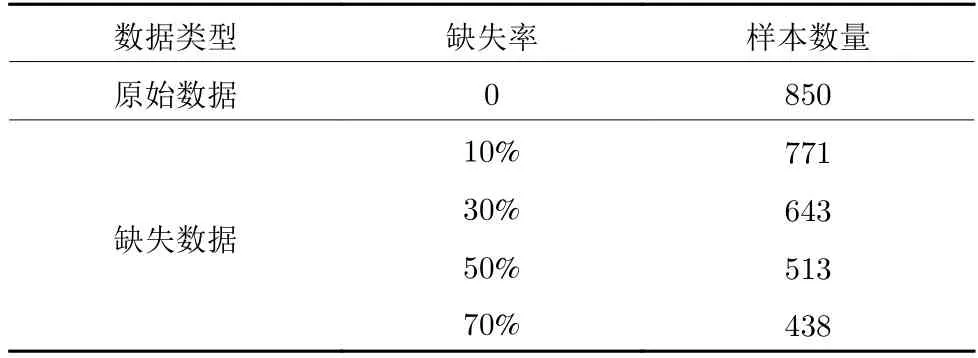
表1 CS2_37 构造的原始数据和不同缺失率下的训练数据Table 1 Original data constructed by CS2_37 and training data with different missing rates

进一步,根据生成数据设置预测所需的数据集模式,将编号为CS2_35、CS2_36、CS2_38 电池的完整数据和CS2_37 截止到600 个循环周期的容量数据作为训练样本,将CS2_37 的600 个循环周期之后的406 个循环周期作为验证样本来评估预测性能.由CS2 电池构造RUL 预测的训练样本和验证样本如表2 所示.

表2 CS2 数据集构造RUL 预测的训练样本和验证样本Table 2 CS2 dataset constructs training samples and validation samples for RUL prediction

根据本文第3 部分所提方法步骤进行数据生成.将训练数据归一化处理后,依次搭建NICE 网络模型和PSO 迭代模型.其中,随着缺失率的提高,可以适当减少 (偶数个) 分块加性耦合层的数量和降低NICE 模型的训练批处理量.粒子的维度为2(充放电循环维度和容量维度),粒子群大小可以设置为2,通过多次生成实验选择保证训练效果的最低迭代次数为15.表3 给出了不同缺失率下的PSONICE 模型参数.其中,第二、三、四列为NICE 模型的结构参数,第五、六列为NICE 模型的训练参数,第七、八列为PSO 的训练参数.

表3 不同缺失率下的PSO-NICE 模型参数Table 3 PSO-NICE model parameters with different missing rates

图5 展示了70% 缺失率下VAE 模型、GAN模型、NICE 模型和PSO-NICE 模型的生成效果图.通过对比不难发现,VAE和PSO-NICE 模型生成数据相较于GAN和NICE 模型更平滑,而在数据分布上,NICE和PSO-NICE 模型对原始数据的拟合度更高.总体上,NICE和PSO-NICE 模型两种方法都可以很好地覆盖锂电池容量整个数据的退化趋势和分布特性,且PSO-NICE 模型生成的数据更接近真实分布.

为研究PSO 算法随机性优化的效果,图6 绘制了不同缺失率下PSO 迭代次数的变化.

从图6 中可以得到,70%和10% 缺失率下的PSO 迭代的优化目标较快稳定,表明缺失率较小或者较大时数据的分布属性较简单,PSO 的优化目标更容易收敛.最终,根据缺失率的大小,PSO-NICE模型生成的数据分布与原始数据的分布误差 (EM距离) 均不同程度稳定在0.02 以下.

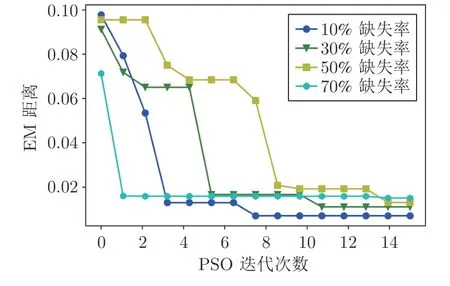
图6 不同缺失率下PSO 迭代优化过程Fig.6 Iterative optimization process of PSO under different missing rates

进一步,为了与VAE、GAN 及DCGAN[11]的生成效果对比,表4 通过EM 距离量化不同缺失率下各方法生成样本与完整样本的误差.由表4 可见,在不同缺失率下,本文所提方法得到的EM 距离均小于其它方法.并且随着缺失率的增大,PSO-NICE模型EM 距离的增幅相对较小,表明其生成分布更接近原始分布.

表4 不同缺失率下各方法生成样本与完整样本的EM 距离Table 4 The EM distance between generation sample and the complete sample under different missing rates

根据PSO-NICE 模型生成的样本数据,选择与缺失值的时间维度最接近的值作为填充值对缺失数据填补,图7 分别绘制不同缺失率下的填补效果.

由图7 可见,在10%和30% 低缺失率的情况下,PSO-NICE 模型对缺失数据填补的精确性较高.在50%和70% 高缺失率的情况下,PSO-NICE 模型对缺失数据填补的精确性较低,某些结果与缺失数据有较大差距.总体上,不论缺失率高低,PSONICE 模型的填补效果均可以保持与原始数据分布的一致性.

图7 不同缺失率下的填补效果Fig.7 Generation effect under different missing rate

为验证预测效果,将PSO-NICE 模型填补后的时序数据按照表2 构造样本,并且全部时序数据要经过滑动时间窗处理.具体地,滑动时间窗统一设置为200,预测步长为1.针对现有常用预测网络(RNN、GRU、LSTM、Bi-LSTM和Bi-LSTMAtt 等),损失函数选择均方误差 (Mean squared error,MSE),优化器选择Adam,调整网络结构和训练参数使各个方法达到最优,相关结果如图5 所示.

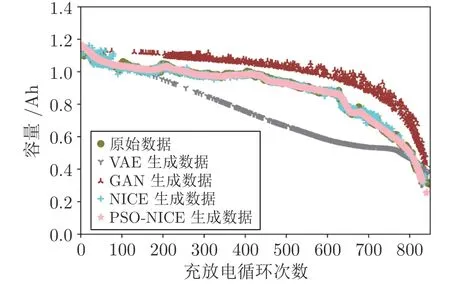
图5 70%缺失率下不同方法的生成效果Fig.5 The generation effect of different methods under 70% missing rate

表5 分别展示了RNN、GRU、LSTM、Bi-LSTM和Bi-LSTM-Att 等现有常用预测网络的参数.需要注意地是,每次预测实验均设置了随机种子,固定预测结果.训练好各类网络后,首先在0%缺失率 (即不缺失) 情况下,从预测起始点迭代预测406 次.预测效果如图8 所示.

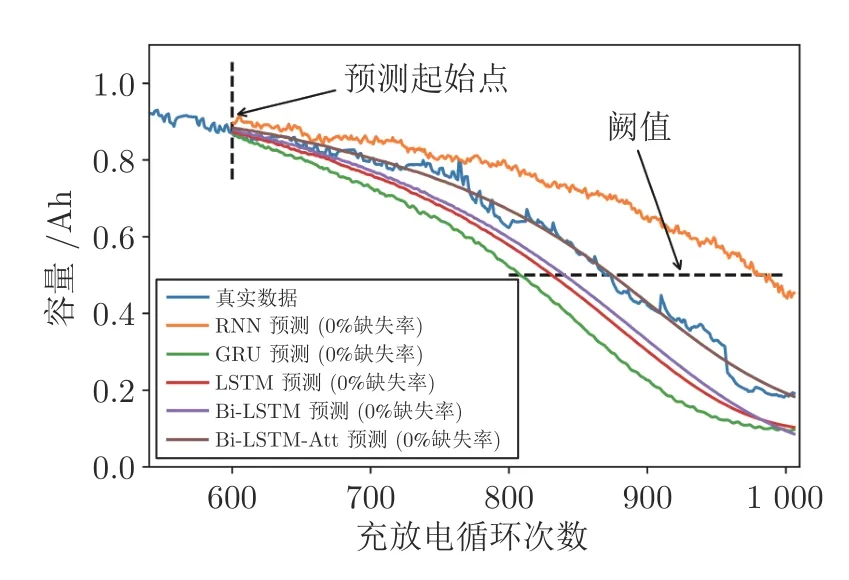
图8 0%缺失率下现有常用方法的预测效果Fig.8 Prediction effect of existing common methods under 0% missing rate

表5 现有常用预测网络的参数Table 5 Parameters of existing common prediction networks

由图8 可见,在0% 缺失率下,对比真实数据,RNN 网络的退化趋势差距较大,并且预测结果滞后,GRU、LSTM和Bi-LSTM 网络的预测退化趋势较好,但预测结果均提前,Bi-LSTM-Att 的预测结果最接近原始数据,且预测趋势更吻合.预测对比实验说明RNN 网络无法捕获长距离的信息,而LSTM-based 方法具有长记忆性,能够获得比GRU更好的预测效果,增添Attention 层后使得整个预测网络关注影响退化趋势的部分重要数据,增加了预测网络可解释性.因此,选择Bi-LSTM-Att 网络来进行剩余寿命预测.

为研究不同缺失率下的填补效果对剩余寿命预测的影响,以10%、30%、50%和70% 四种缺失率为例,图9 展示了同一Bi-LSTM-Att 网络的预测效果.

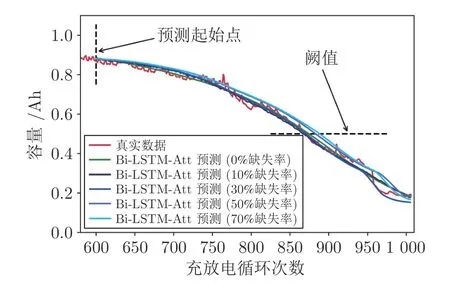
图9 不同缺失率填补后Bi-LSTM-Att 的预测效果Fig.9 The prediction effect of Bi-LSTM-Att after filling with different missing rates

为了更清晰地量化预测效果,采用均方根误差(Root mean square error,RMSE)和决定系数 (Rsquared,R2) 两个指标衡量预测的准确性,并将结果绘制于表6.RMSE是逆向指标,该值越小越好,而R2是正向指标,该值越大越好,范围为 ( 0,1).计算公式如下:其中,yi是各个时刻的真实值,是各个时刻的预测值,是各个时刻的均值.

表6 不同预测方法的效果评估Table 6 Effectiveness evaluation of different forecasting methods

由表6 不难看出,Bi-LSTM-Att 模型的RMSE和R2均小于其他方法,但是运行时间较长.此外,随着缺失率的增加,Bi-LSTM-Att 预测精度增大幅度较小,再一次表明所提缺失数据生成方法能够高效捕捉时间序列的退化信息的优越性.

进一步,考虑到样本的完全随机缺失机制,需要讨论其对预测结果影响的稳定性分析,检验模型的鲁棒性.具体地,仍然以10%、30%、50%和70%四种缺失率为例,仅仅改变真实数据的缺失位置,再通过PSO-NICE 网络和Bi-LSTM-Att 网络进行缺失数据生成填补、剩余寿命预测任务,重复试验,得到预测相关效果如图10 所示.

同时,为了量化预测效果,采用RMSE衡量预测的准确性,相关量化结果如表7 所示.

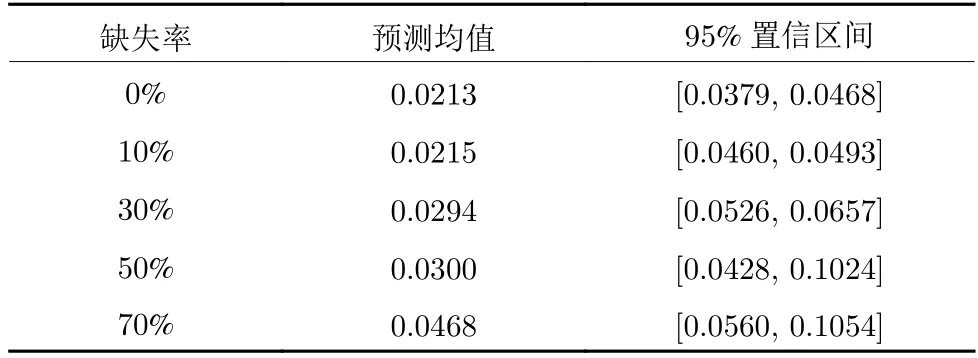
表7 不同缺失率填补后Bi-LSTM-Att 重复预测量化结果Table 7 Quantification results of Bi-LSTM-Att repeated prediction after imputation with different missing rates

通过对比观察图10 不难看出,四种缺失率下,Bi-LSTM-Att 模型重复实验95% 的预测置信区间均能够很好地覆盖真实数据,且预测均值与真实数据拟合程度较高,表明PSO-NICE 模型对缺失数据生成的稳定性和鲁棒性较好.

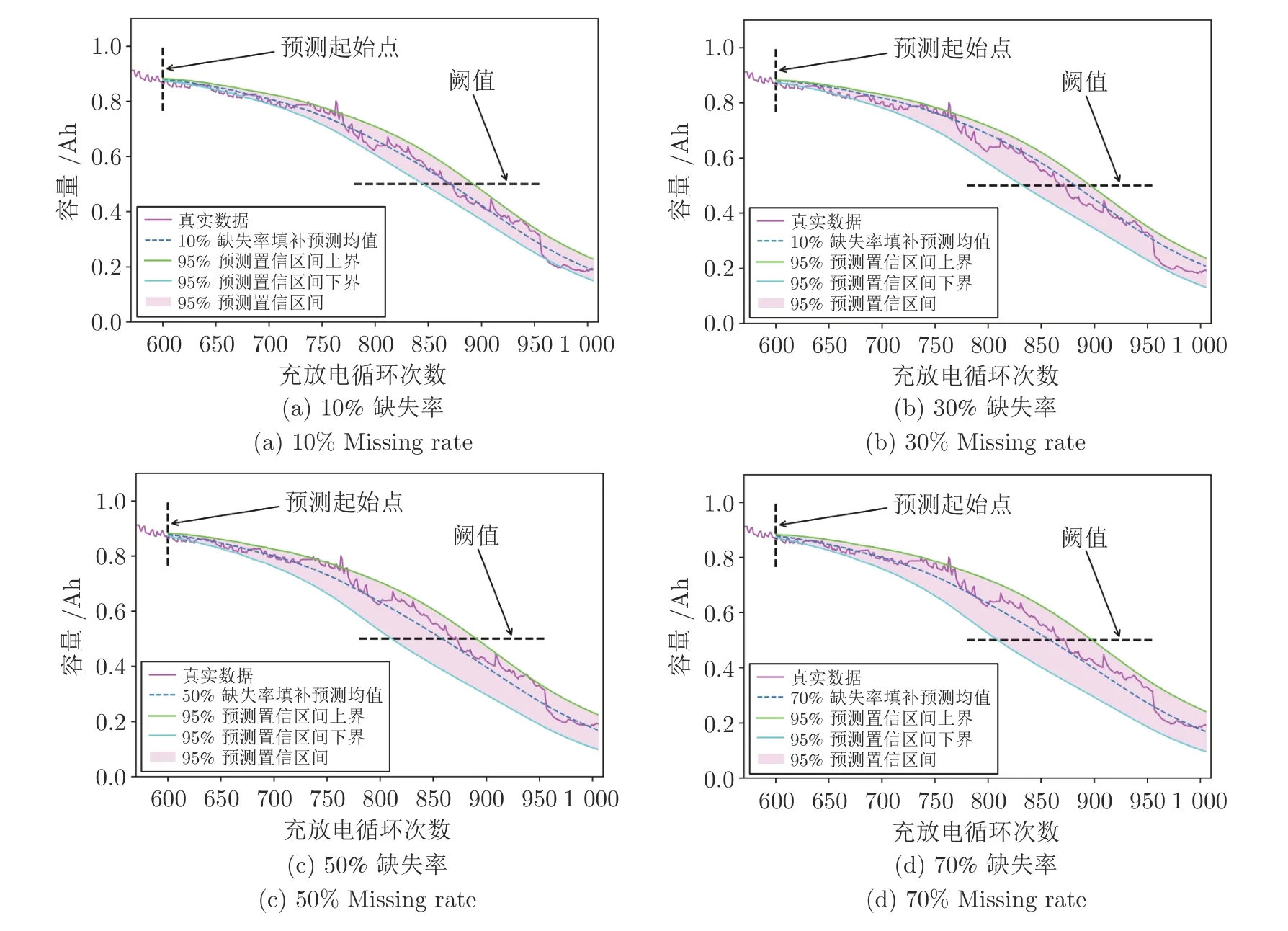
图10 四种缺失率填补后Bi-LSTM-Att 重复预测效果Fig.10 Bi-LSTM-Att repeated prediction effect after four missing rates imputation

5 结论

针对缺失数据生成模型精度低和训练速度慢的问题,提出一种基于流模型框架的缺失数据生成方法,可以获得较好的生成效果,最后通过锂电池实例进行验证.工作的主要创新如下:

1) 基于流模型框架,将一维时序缺失数据输入NICE 深度生成模型,通过无监督方式学习缺失数据背后的真实分布,进而对缺失数据进行充分填补,得到完整意义下的时间序列数据.

2) 基于NICE 深度生成模型,在NICE 反向生成阶段,通过引入PSO 算法,迭代优化其退火参数,将深度生成模型由无监督变成有监督,能够更精准地学习缺失数据背后的真实分布,提升对缺失数据填补的精度,得到更完整意义下的时间序列数据.

本文基于流模型框架,通过建立NICE 模型和PSO-NICE 模型,实现了对一维时间监测序列完全随机缺失下系统缺失数据的生成及剩余寿命预测的应用.在未来的研究中,将进一步考虑现场实际环境的复杂关系,对不同缺失机制、多维度时间监测序列的缺失数据生成和RUL 预测问题进行更深层次的探索和研究.