复杂工业过程非串级双速率组合分散运行优化控制

赵建国 杨春雨

冶金、化工、电力等现代工业一般由多个环节串联、并联或耦合而成,往往呈现模型维数高、多时间尺度耦合、动态不确定性等综合复杂性.传统设计只考虑设备层过程控制的控制方法,无法实现运行过程的优化,容易导致产品质量低下和能源浪费[1-2].因此,综合考虑设备单元过程控制和运行过程优化控制的复杂工业控制问题引起了学术界和工业界的广泛关注[3-5].运行优化控制(Operational optimal control,OOC)的内涵是在保证过程控制安全运行的条件下,优化运行指标,从而提高产品质效并降低生产消耗[6].

工业过程运行优化控制目前普遍采用如图1 所示的串级控制结构,外环利用设定值优化器,根据期望运行指标r*,确定设备层过程控制回路设定值内环控制器用于实现设定值跟踪,进而使实际运行指标r(t) 控制在目标值r*附近[7].得益于上层优化与底层控制的独立处理,以及能逐步设计内外环控制器的优势,工程师和学者们已提出很多串级控制结构下的研究成果,如实时优化、模型预测控制、自优化等基于数学模型的方法,以及迭代学习、模糊逻辑、神经网络等基于数据驱动的智能控制方法.

图1 工业过程串级运行优化控制结构Fig.1 The cascade structure of operational optimal control in industrial process

在串级控制框架下,文献[8]面向设备层输出是运行层输入且运行过程含有未建模动态的串联工业过程,提出了基于多模态切换和神经网络补偿的鲁棒自适应运行控制方法.文献[9]进一步将该方法拓展到双速率控制中.文献[10]利用参考调节器,处理了具有不可行设定值且输入受限的运行优化问题.受生物学习机制启发,增强学习(Reinforcement learning,RL)能在未知环境下不断反馈更新寻找系统最优控制策略[11-12].因其具有突出的自学习能力,促使很多学者探索基于RL 的复杂工业过程控制方法.为处理运行过程模型难以获取情况下的运行优化控制问题,文献[4]结合模型预测控制和Q-学习算法[13],提出了多速率运行优化控制方法.文献[14]借助史密斯预估器,提出了双Q-学习算法,解决在无线网络环境中外环回路传输存在丢包情况下的混合选别浓密过程控制问题.文献[15-17]研究了非线性工业过程的RL 运行控制方案.串级控制结构是一种典型的分层模式,首先设计内环反馈回路,然后基于设备层过程控制回路与运行层运行过程构建的增广系统设计外环反馈回路.然而内环过程控制回路的跟踪误差或者外环设定值优化误差对整个运行优化和控制有显著的负面影响[8].此外,随着现代工业朝着复杂化与大型化方向发展,基于内环稳定的全阶增广模型的外环设定值优化设计具有较大计算量,容易发生 “维数灾”和 “病态数值问题”[18].

为实现同时调节设备单元与运行过程,提高运行指标跟踪性能,进而提质增效,已有学者研究了工业过程的非串级控制模式[5,18].如图2 所示,在非串级运行优化控制中,过程控制设备与运行过程组成的工业过程被建模成一个整体大规模系统,并通过直接优化控制输入u1(t),···,um(t) 驱动实际运行指标r(t) 跟踪目标值r*[18].

图2 工业过程非串级运行优化控制结构Fig.2 The non-cascade structure of operational optimal control in industrial process

工业过程不同层级之间具有不同时间尺度,面向过程控制的设备层具有快时间尺度动态,面向运行过程的运行层具有慢时间尺度动态[3-4].奇异摄动系统是建模多时间尺度系统的有效工具,其中奇异摄动参数表示慢快动态分离的程度[19-20].通过奇异摄动理论,全阶模型控制问题可简化为降阶慢快子系统控制问题,从而有效避免了控制器设计时存在的 “维数灾”和 “病态数值问题”,而且对于充分小的奇异摄动参数,独立子系统的稳定性蕴涵了整体系统稳定性[21-22].文献[5]利用奇异摄动理论将复杂工业过程运行优化问题刻画成慢快子系统的最优控制问题,并提出了双Q-学习的数据驱动控制算法,不仅实现了运行指标的跟踪,还解决了设备层高频振动抑制问题.文献[18]针对具有多个设备单元的工业过程,提出了数据和模型混合驱动的非串级组合分散控制方法,有效降低了控制器的通讯量与计算量.非串级运行优化控制的研究目前处于起步阶段,还有许多亟待解决的科学难题.一方面,工业过程广泛存在慢快时间尺度耦合现象,应用在串级双速率控制中的提升技术很难借鉴到非串级控制框架中;另一方面,不同设备单元间的互联对整体系统稳定性分析和优化控制提出新的挑战.

本文充分考虑复杂工业过程特点,整合奇异摄动理论[19]与RL 技术[11],针对一类由多个快变且互联的设备单元与慢变且模型未知的运行过程串联组成的工业过程,提出一种数据和模型混合驱动的非串级双速率组合分散运行优化控制方法.主要贡献概括如下:

1)区别于已有非串级控制工作,相比文献[5],本文对解耦后的慢快子系统进行异步采样,设计双速率组合控制器,解决了因各层级间采样周期不同而难以统一控制的问题,同时还处理了设备层存在互联时的分散控制问题,给出了具有稳定性保证的快子系统分散次优控制设计方法;相比文献[18],本文不仅设计了双速率控制器,还进一步考虑了多设备互联时的分散控制问题.

2)现有基于RL 的工作[3-5,14,16-18,23-24]使用折扣代价的最优设定值跟踪控制表达,然而在运行过程模型未知时难以确定折扣因子的下界[25],致使闭环系统稳定性无法保证.本文通过定义增量式的最优设定值跟踪控制表达[26],移除了代价函数中的折扣因子,避免了折扣因子带来的弊端.

本文的组织结构如下:第1 节描述基于奇异摄动的工业过程非串级双速率组合分散运行优化控制问题;第2 节设计慢快子系统优化控制问题的解,同时给出慢子系统问题的解存在条件以及保证快子系统稳定的充分条件;第3 节设计运行优化控制策略,提出数据和模型混合驱动的组合控制方法,并进行性能分析;第4 节利用浮选过程进行仿真实验,验证所提方法对运行指标的跟踪能力;第5 节对本文工作进行全面总结.

1 基于奇异摄动的工业过程非串级双速率组合分散运行优化控制问题描述

本部分首先将工业过程建模成一类快动态互联且慢动态未知的奇异摄动系统;然后依据奇异摄动理论对全阶模型进行降阶处理,分离为慢采样的慢子系统和快采样的快子系统;最后分别刻画慢快子系统的最优控制问题.

1.1 工业过程建模

考虑图3 所示的工业过程,其动态模型由设备层过程控制对象的动态模型和运行层运行过程的动态模型两部分构成[3-5,8,15,18].设备层对象的执行器装置,如阀门、电振机、水泵等变化速率比较快,而与质量、效率和消耗等运行指标相关的运行层动态变化缓慢,同时设备层输出为运行层输入,因此工业过程具有显著的慢快时间尺度耦合特性[3,5].因运行指标的束缚,不同设备单元之间往往存在互联影响[3],而运行过程中复杂的物理、化学、相变等反应或变化[27],导致其数学模型很难获取.基于以上分析,本文将工业过程建模为一类由多个快变且互联的设备单元与慢变且模型未知的运行过程串联组成的奇异摄动系统.

图3 多设备单元互联的工业过程Fig.3 Industrial process with multiple and interconnected unit devices

设备层动态模型为

1.2 异步采样的慢快子系统

为避免基于工业过程整体模型控制设计时存在的 “维数灾”和 “病态数值问题”,并满足设备层与运行层的双速率采样要求,本节将全阶系统(3)解耦为两个异步采样的离散化慢、快子系统.

将式(3)改写为紧凑形式

为了准确获取设备层的快动态信息,参照文献[21],把系统(4)离散化为

因为慢变量在瞬时可认为是常值,把式(6)代入式(5b),可得快采样的快子系统模型为

1.3 运行优化控制问题

本文中非串级双速率组合分散运行优化控制任务为在假设1 下,设计基于设备层数据快采样与运行层数据慢采样的分散组合控制器,使实际的运行指标r跟踪期望的设定值r*.为了达到这一目标,分别对降阶系统(9)和(10)定义优化控制问题.

问题 1.寻找慢子系统(9) 的最优控制us(k),相对如下代价函数

注 2.快子系统(10)的控制问题是设计分散形式的uif(n),进而实现设备单元控制器之间的独立运行.由于不同设备单元间的互联项,无法设计最优的控制策略.因此本文考虑次优的分散控制器,并受文献[28]和文献[29]启发,将借助收敛因子γ来保证快子系统的整体稳定性.

2 工业过程慢快子系统优化控制问题求解

2.1 慢子系统优化控制

结合式(14)和式(15)可知,问题1 中的优化问题能转化为最优调节器.受文献[26]启发,引理2 给出了问题1 的可稳解存在且唯一的条件.

引理 2.在假设3 下,如果

通过初等变换,可观性秩条件判据满足

注 3.由文献[30]可知,式(16)也是渐近跟踪控制问题可解的充分条件.虽然在假设1 下无法直接判断式(16)是否成立,但是对于具体的复杂工业过程来说,往往可知其运行层的名义模型(也可用输入输出数据进行辨识获得),进而判断引理2 中式(16)的条件是否满足.

根据最优控制理论[31],在引理2 的条件下,系统(14)相对代价函数(15)的最优控制输入为

考虑到下文无模型控制器设计需要,设慢子系统初始控制序列为us(0)=Ks,1zs(0),把上式等号两端分别相加,可得

定理 1.在控制输入(19)的作用下,闭环慢子系统(9)渐近稳定,并且跟踪误差es(k)=rs(k)-r*渐近收敛到零.

证明.把式(19)代入式(14),有

2.2 快子系统优化控制

忽略互联项,快子系统(10)变为

根据最优控制理论[31],系统(20)相对代价函数(13)的最优控制输入为

本文设计控制输入(21)为优化问题2 的次优解,下面将对快子系统(10)的稳定性进行分析.为此,重写式(10)为紧凑形式

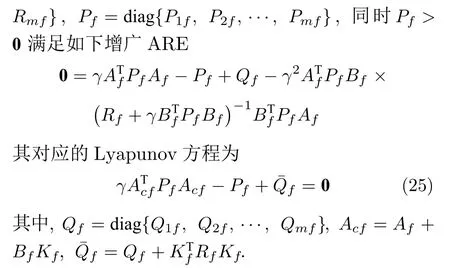
定理 2.设互联快子系统(23)的控制输入为式(24),如果

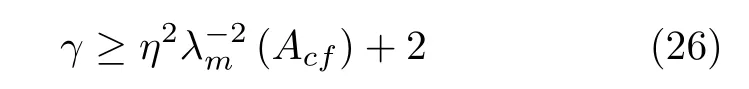
则其闭环系统是渐近稳定的.

证明.对互联快子系统(23)选取Lyapunov 函数

3 非串级双速率组合分散运行优化控制设计

3.1 运行优化控制策略

由前两节的分析可知,依据非串级运行优化控制路线,工业过程动态模型(1)和动态模型(2)能建模为一类快动态互联且慢动态未知的奇异摄动系统(3),其运行指标设定值跟踪控制描述为慢动态的输出跟踪问题.参照奇异摄动理论,离散化的工业过程模型(5) 能被分解为异步采样的慢子系统(9)与快子系统(10),通过定义两个独立的优化问题1和问题2,可直接设计设备层的双速率组合分散控制输入.因此根据子系统采样周期,设置设备层采样周期为h,运行层采样周期为T,h与T之间满足关系式T=Nh.由于运行层运行过程模型参数未知,使慢子系统问题的解(19)无法直接获取,故本文采用Q-学习算法,利用工业运行数据在线学习慢子系统最优输入的控制增益,实现慢动态输出跟踪设定值的目的,同时利用设备层模型信息计算快子系统优化问题的解(21),并判断定理2 中的收敛因子条件,进而完成非串级双速率组合分散控制器的设计.

3.2 基于Q-学习的组合控制器

为了解决运行过程模型难以获取的难题,下面设计基于Q-学习的数据驱动算法求解慢子系统的控制输入.定义代价函数(15)的值函数为

对于辅助系统(14)的一个固定增量形式的控制输入 Δus(k)=KsZs(k),其闭环系统可递推为

根据式(27)和式(29),表达如下Bellman 方程

参照文献[12]和Bellman 方程(30),定义Q-函数

慢子系统(9)是虚拟系统,基于其构造的辅助系统(14)的状态Xs(k) 与输入 Δus(k) 的数据信息无法直接获取,受文献[5,18,22,32]的启发,本文将借助引理1 中的近似性进行数据替换.为此,定义

通过式(33)和式(35),针对运行过程模型未知问题,利用算法1 来设计慢子系统的最优控制增益.

算法 1.基于Q-学习的策略迭代算法

注 5.算法1 的具体求解过程类似文献[12-13],这里不再赘述.使用基于值迭代的Q-学习算法能放宽初始稳定控制增益条件,详见文献[33].最近,自适应动态规划(Adaptive dynamic programming,ADP)[34]方法已经广泛应用于最优输出调节领域设计无模型控制器,解决系统输出跟踪控制问题,如文献[29]和文献[35].相比存在的ADP 方法,本文只需求解一个最优控制问题,而文献[29]和文献[35]还要额外求解一个静态的优化问题,因此本文方法降低了设计复杂度;此外,本文基于Q-学习的跟踪方法所学未知变量较少,还具有计算方面的优势.

实际上,算法1 中的数据替换会导致计算误差,故算法1 学习得到的控制增益可写为=Ks+ΔKs,其中,ΔKs是关于ε的摄动[22,32].在执行完算法1后,基于式(19)和式(24),构造如下双速率组合控制器

进一步,表达显示的设备层控制输入的分散形式,即

3.3 性能分析

由式(41)可知算法1 收敛时慢子系统的反馈增益为

定理 3.设离散化的工业过程(5)的控制输入为(39),则存在某个ε* ＞0 ,使对所有ε∈(0,ε*],闭环系统(5)是渐近稳定的.

证明.首先根据文献[21]可知,如果慢快子系统(9)与(10)是渐近稳定的,那么存在某个ε* ＞0,使对所有ε∈(0,ε*],快采样离散时间奇异摄动系统(5)是渐近稳定的.对于快子系统,由定理2 可知,当设计的收敛因子满足条件(26)时,快子系统(10)是渐近稳定的;对于慢子系统(9),由矩阵的连续性可知,当奇异摄动参数ε充分小时,通过算法1 学习到的反馈增益(42)的摄动误差 O (ε) 不会影响闭环矩阵=(As-BsKs)+O(ε) 的特征值在单位圆内的特性,借鉴定理1 的路线可证闭环慢子系统也是渐近稳定的. □

注 6.文献[3-4,9,14-17]提出的双速率运行优化控制方案都是基于提升技术,将设备层过程控制回路与运行层运行过程的采样周期提升至相同框架下,然后对增维的广义工业过程模型进行控制设计,若设备层与运行层之间的时间尺度相差较大,使用提升技术会导致系统阶数过高且计算量显著增加,容易发生 “维数灾”和 “病态数值问题”.相比之下,本文方法利用奇异摄动降维有效避免了这些缺陷.

注 7.非串级双速率控制器(39)含有运行指标跟踪误差的积分,因积分器的作用,使其可抑制常值或分段常值的干扰,保持运行指标的无静差跟踪.在实际中这些干扰可能来自模型线性化误差、外界环境变化、原材料波动以及生产设备老化等环节.因此,本文方法对于非串级控制具有工程应用价值.

注 8.本文所提非串级双速率控制方法具有一般性,能推广到更复杂的奇异摄动系统.如文献[22]中的多参数奇异摄动系统,只需在慢子系统设计时进行相似的坐标变换,即可按照本文路线进行非串级双速率分散控制器设计.对于非线性奇异摄动系统,可参照文献[36]在解决快子系统含有慢时变参数的影响下,设计非串级双速率控制器.

4 仿真实验

本节以浮选过程为例验证所提非串级双速率组合分散运行优化控制方法的有效性.

4.1 浮选过程工艺流程

浮选过程是借助矿物的亲水或疏气性质进行矿物分离的[3].本文选取图4 所示的黄铜矿单浮选过程,其由槽体、给矿泵、搅拌机、空气集流器、阀门等装置组成.在浮选过程中,来自磨矿过程的矿粒首先与一定比例的水和浮选药剂被给矿泵输送至浮选槽,被选矿物在药剂的作用下产生亲水性,通过空气集流器在槽体内会产生大量气泡,从而将被选矿物带入泡沫尾,达到分层的效果.之后被选矿物在泡沫尾中经精矿阀门流出,杂质等在矿浆中经尾矿阀门流出,实现分离被选矿物与杂质的目的.浮选过程优化目标是将精矿品位r1与尾矿品位r2两个运行指标控制在目标值附近.

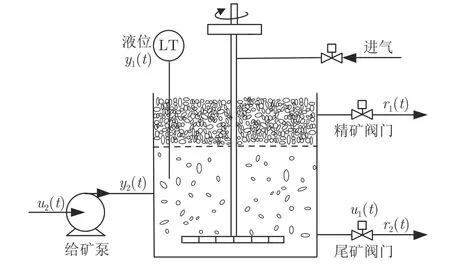
图4 单浮选槽示意图Fig.4 Configuration of single flotation cell

浮选过程运行控制可描述为设备层与运行层两层结构[3].设备层通过改变尾矿阀门开度u1与给矿泵转速u2来改变泥浆液位高度y1和给矿矿浆流量y2. 运行层通过改变液位高度y1和矿浆流量y2来控制精矿品位r1和尾矿品位r2.

设备层的数学模型为[3]

其中,A为浮选槽底面积,g为重力加速度,k1,k0为与阀门和给矿泵相关的系数,τ为时间常数.

运行过程的数学模型为[16]

4.2 仿真结果

设置精矿品位r1和尾矿品位r2的期望设定值为17.35和0.75[3],设备层泥浆液位高度和矿浆流量变化是快过程,其采样周期为h=0.05 s,运行层泥浆质量和泡沫质量变化是慢过程,其采样周期为T=1s,分别选取代价函数(12)和代价函数(13)的加权矩阵Qs=1 000 12,Rs=12,Q1f=100,Q2f=1,R1f=R2f=1.

本文所提Q-学习方法仅使用运行过程动态模型来生成数据,实际设计时无需其模型参数.选择不同频率的正弦信号为探测噪声,并执行算法1 学习慢子系统最优控制增益,由图5和图6 可知,,在迭代过程中与其最优值H,Ks差的2 范数逐渐减小且趋于零.从图7和图8 的仿真结果可以看出,系统运行65 s 后,所提非串级双速率组合控制器能很好地驱使浮选过程运行指标r1和r2跟踪设定值和.而且,通过图9 能清晰观察到矿物品位的跟踪误差e1=r1,e2=r2都渐近收敛到零.

图5 内核矩阵的收敛性Fig.5 Convergence of to its ideal value H

图6 控制增益 的收敛性Fig.6 Convergence of to its ideal value Ks

图7 精矿品位跟踪曲线Fig.7 The tracking performance of the concentrate grade to its set-point

图8 尾矿品位跟踪曲线Fig.8 The tracking performance of the tail grade to its set-point

图9 浮选过程矿物品位跟踪误差曲线Fig.9 Evolution of the ore grade tracking error

此外,为验证在复杂环境下所提方法的抗干扰能力,在设备层输入通道中加入如图10 所示的扰动来模拟实际工况变化.从图11、图12 中可看出,尽管浮选过程受到干扰的影响,但在非串级双速率控制器作用下每次精矿品位r1和尾矿品位r2依然能稳定在其设定值.该仿真结果表明,本文所提具有误差积分类型的非串级双速率运行优化控制方法具有良好的鲁棒性和抗干扰能力.

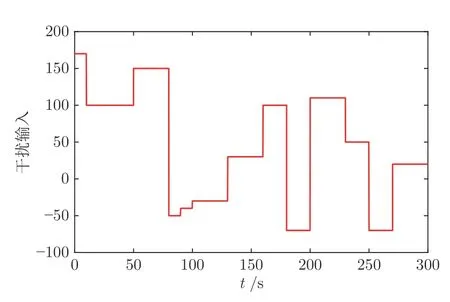
图10 扰动曲线Fig.10 Evolution of the disturbance

图11 扰动下精矿品位跟踪曲线Fig.11 The tracking performance of the concentrate grade to its set-point under disturbance

图12 扰动下尾矿品位跟踪曲线Fig.12 The tracking performance of the tail grade to its set-point under disturbance

4.3 对比仿真

首先,将本文方法与文献[18]的非串级分散控制方法在相同实验条件下进行对比.由于文献[18]没有考虑设备层间的互联,因此为实现分散控制器设计,这里直接忽略设备层互联项,然后将文献[18]的控制策略作用于浮选过程中.所得文献[18]的慢快子系统控制器参数为

为评价两种方法的控制性能,引入绝对误差积分(Integral absolute error,IAE)与误差均方差(Mean square error,MSE)[3,5,14],即

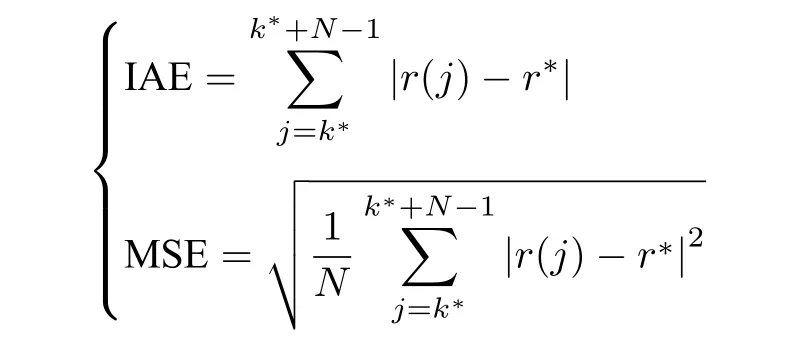
从表1 中可见本文方法的评价性能均优于文献[18]的结果,主要原因是文献[18]使用了带有折扣因子的代价函数,而这种折扣的跟踪控制方法往往无法实现零稳态误差跟踪[13].

表1 对比仿真评价指标Table 1 Performance index of comparison simulation

其次,将本文方法与文献[5]的非串级控制方法在相同实验条件下进行对比.由于文献[5]没有考虑多设备单元情况,因此这里将设备层模型当成一个整体情况来处理.从图13、图14 可以看出基于文献[5]的方法浮选过程精矿品位和尾矿品位也能近似跟踪上其设定值,可是对比图7、图8 发现其达到稳态时间较长且存在稳态误差.主要原因也是其使用了基于折扣代价函数的最优跟踪方法.

图13 基于文献[5]的精矿品位跟踪曲线Fig.13 The tracking performance of the concentrate grade to its set-point using the method in references [5]

图14 基于文献[5]的尾矿品位跟踪曲线Fig.14 The tracking performance of the tail grade to its set-point using the method in references [5]

5 结论

本文针对多设备单元互联、多时间尺度耦合以及运行层模型未知的一类工业过程,研究了非串级双速率组合分散运行优化控制问题.将奇异摄动理论与RL 技术相结合,提出了一种工业过程双速率组合分散控制方法.利用奇异摄动理论将工业过程解耦为异步采样的慢快子系统,采用数据驱动的Q-学习算法求解慢子系统问题,实现了运行指标的跟踪控制,同时求解基于模型的快子系统优化问题,实现了多设备单元之间的分散控制.相较串级控制结构,本文方法能同时调节设备单元与运行过程,设计过程不受设备层与运行层间时间尺度分离程度的影响,避免了 “维数灾”和 “病态数值问题”.对浮选过程进行的仿真实验验证了所提方法的有效性.