面向新能源电力系统的容量市场出清模型

张柏林， 雷 绅， 吴 锋， 吴 雄， 赵文成

(1.国网甘肃省电力有限公司， 甘肃 兰州 730030； 2.西安交通大学电气工程学院， 陕西 西安 710049)

1 引言

深化电力体制改革和构建以新能源为主体的新型电力系统是实现“碳达峰”和“碳中和”战略目标的重要举措。目前国内电力体制改革在充分借鉴国外电力市场经验[1,2]的基础上，结合自身实际取得了阶段性成果，改革红利逐步释放并普惠社会[3]。同时随着以新能源为主体的新型电力系统的构建，国内新能源装机规模快速增长，储能电站也快速发展以促进新能源消纳[4]，但高比例新能源的接入给电力系统的安全稳定运行带来巨大了挑战[5,6]，系统发电充裕度不足，风险明显上升，影响系统可靠性。与此同时，现阶段国内普遍缺乏有效的容量补偿机制，进一步加大了这一风险。因此需建立适应新能源快速发展的电力市场机制，通过合理的容量补偿机制来确保发电容量充裕性[7-9]，在加快构建新型电力系统的同时保障能源供应安全。

容量市场作为一种有效的电力市场环境下发电容量充裕度保障机制，在多个国家实施并取得了良好的运行效果[10,11]。市场出清模型是决定容量市场运行效果的关键因素，国外对于容量市场的研究开展较早，提出了多种容量市场出清模型[12-14]，文献[12]提出了一种储能资源深度参与的容量市场出清模型。文献[13]则提出了考虑柔性需求的容量市场模型。文献[14]提出了针对分散电力系统的容量市场模型。上述模型都有一定借鉴意义，但国内外电力系统特性迥异，不能很好适应我国构建新型电力系统的发展趋势。国内在介绍和借鉴国外经验的基础上也开展了进一步研究[15-19]，文献[15,16]介绍了英国容量市场的交易机制并给出了对我国的启示意义。文献[17]对美国容量市场进行了分析，指出其对我国华东容量市场建设的参考意义。文献[18]提出了一种适应清洁能源发展、考虑现货电能量交易潜在影响的新型容量市场机制。文献[19]考虑了容量资源结构等能源发展约束，提出了兼容多目标调控需要的新型容量市场机制。国内现有文献充分考虑了我国电力系统特性，但大多侧重于机制整体设计，对出清模型研究不够深入，此外对于新型电力系统中高比例新能源接入时系统可靠性问题考虑的不够。

因此本文提出了一种面向新能源电力系统的容量市场出清模型，以期解决以新能源为主体的新型电力系统的发电容量充裕性问题，提高系统可靠性。本文首先以容量成本最小为目标，提出了一种考虑可靠性约束的容量市场出清模型，同时计及了网架、容量平衡等约束。其次，将所提模型构建为双层模型进行求解，实现系统在经济性与可靠性之间寻优，以最经济的市场方式保障系统安全稳定运行。最后，以甘肃省实际数据进行了算例分析，验证了模型的有效性。

2 容量市场出清模型

容量市场的出清即是经济性和可靠性之间的寻优问题，在保障系统足够的发电容量充裕度前提下提高经济性。因此，提出如下容量市场出清模型。

2.1 目标函数

电力容量市场中不同机组的容量成本以各机组报价为准，市场以系统采购容量成本最小为目标，目标函数如下：

(1)

式中，NZ为系统内电气分区总数；ai,j为j区第i台传统机组的报价；am,j为j区第m个储能电站的报价；Gi,j和Pm,j分别为j区第i台传统机组和第m个储能电站申报的有效容量；θj和γj分别为j区中传统机组及储能电站的集合。

2.2 约束条件

(1)机组容量约束

机组在市场中可申报容量为其最大有效容量，即机组额定容量的基础上考虑其强迫停运率，可由式(2)和式(3)表示。

(2)

(3)

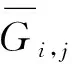
(2)储能容量约束

对于储能电站，一般有功率和能量两种额定容量，功率额定容量以MW表示，能量额定容量以MW·h表示，文中采用储能电站的功率额定容量。目前储能的有效容量支撑一般在2～4 h，因此引用文献[13]的方法来计算储能的有效容量。

(4)

(5)

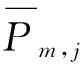
因此，储能电站容量约束可以表示为：

(6)

(3)容量平衡约束

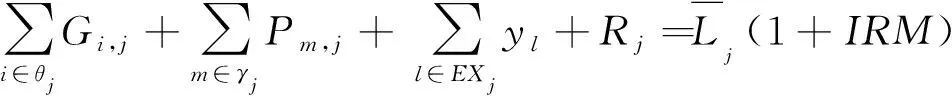
(7)

(8)

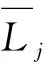
(4)可靠性约束

容量市场的重要目标就是保障系统可靠性，本文以失负荷期望(Loss Of Load Expectation，LOLE)作为可靠性指标，对系统可靠性进行约束。

LOLE(IRM)≤β

(9)

式中，β为设定的可靠性标准。

2.3 新能源参与市场措施

考虑到加快构建新能源为主体的新型电力系统的要求，新能源机组作为市场价格接受者优先出清，以其置信容量作为有效容量进行结算。

3 模型求解

可以看出，上述模型中除可靠性约束外，目标函数和其他约束都是线性的，由于可靠性约束的加入使得模型难于求解，因此需要对可靠约束进行分析。可靠性评估方法中非序贯蒙特卡洛法的模型简单，内存占用少，所需原始可靠性数据也相对较少，比较适合应用在大规模电力系统可靠性评估中，本文采用非序贯蒙特卡洛法进行可靠性评估。

(1)非序贯蒙特卡洛第k次抽样的失负荷量可以由如下模型计算：

(10)

(11)

(12)

(13)

0≤ΔLj,k,t≤Lj,t

(14)

(15)

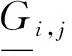
可以看出式(11)的约束中计及了新能源的预测误差，在研究含有大量可再生能源的电力系统可靠性时，一般将风电和光伏出力的预测误差看作随机变量。由于随机变量的加入，使得模型求解变得困难，考虑到容量市场作为远期市场，在精度的要求方面要低于实时调度，因此将式(11)松弛成式(16)所示的机会约束，即在极端条件下可以不满足约束，但是这种极端条件出现的可能性小于某一概率水平，即转化成机会约束模型。机会约束模型中机会约束条件的处理会造成机会约束规划模型求解速度慢。

(16)

式中，Pr(·)为事件概率；π为设定的置信水平。传统方法利用随机模拟的方式处理式(16)所示的机会约束条件时，对任意时刻t，首先按照约束条件中随机变量的分布规律产生足够数量的随机样本，之后利用产生的样本验证式(17)成立与否，对成立的次数进行统计。若成立次数与验证次数的比值大于等于π，则判定机会约束条件(式(16))成立；反之，则判定不成立。

(17)

受随机模拟法求解过程的启发，可以对随机变量按照分布规律进行Nsa次采样，第sa次采样的采样值记作δsa。当采样次数足够大时，机会约束条件可由下面混合整数线性约束条件代替。

(18)

(19)

dt(sa)=0或1 ∀1≤sa≤Nsa

(20)

式中，M为一个足够大的正数；dt(sa)为0、1变量，当dt(sa)=1时，式(17)成立，当dt(sa)=0时不成立。由式(18)的约束可知，对于所有Nsa组采样值，式(18)至少成立Nsa次时，即与约束条件式(16)等价。

同时，还应满足储能运行约束，主要有充电、放电约束和荷电状态约束等，在此不再赘述。

(2)可靠性计算：

(21)

(22)

式中，K为总抽样次数；NT为模拟时间。

显然采用蒙特卡洛计算可靠性指标使得模型成为双层优化模型，此双层优化问题具有一种特殊的结构，即上层模型和下层模型仅由变量Gi,j和Pm,j组合而成，即市场出清的各类机组容量。此外，Gi,j和Pm,j直接由变量IRM决定。

因此可以将模型进行分解求解，原理图如图1所示。把整个问题分解成两个子问题，交替迭代以获得最优解。即由式(1)～式(9)组成的子问题1和由式(10)～式(20)组成的子问题2。

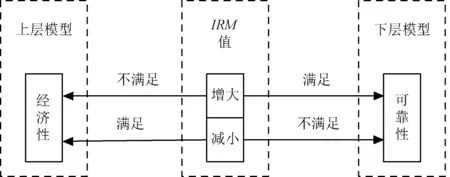
图1 模型求解原理图Fig.1 Model solving principle

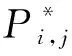
因此上述模型上下层之间是由IRM一个变量联系的，根据图1所示的模型原理图，求解模型就是寻找一个最优的IRM值，使得在满足系统可靠性的前提下经济最优。寻找最优值的这一过程可以用二分法来实现。首先，给定IRM值的上限UB和下限LB，使IRM等于UB和LB的中值，然后根据上述的分解算法计算可靠性指标LOLE，如果LOLE能够达到设定的指标值，则降低UB的值，也就是降低了IRM，使满足系统可靠性指标的同时能更少地出清容量降低成本，反之则升高LB的值以满足系统可靠性。不断迭代，直到UB和LB的差值小于给定的精度ε，此时的值就是在满足系统可靠性指标的前提下最优的出清容量，也即最小的容量成本。整个求解流程如图2所示。

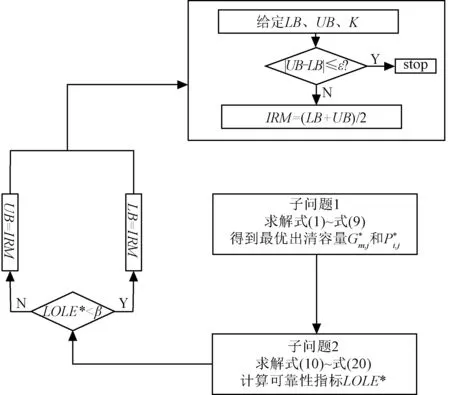
图2 求解流程图Fig.2 Flowchart of decomposition method

4 算例分析

以甘肃省电网实际数据进行算例验证，现阶段全省装机容量充裕，预计至“十四五”末开展容量市场，提前三年进行拍卖即首个交付年为2028年。

4.1 计算条件

(1)网架结构。根据甘肃电网地理接线图及电气特性，将全区分为如图3所示的嘉酒地区、河西地区、兰州中心地区、平凉庆阳地区以及天水陇南地区5个分区开展容量市场，依次编号为1～5分区。

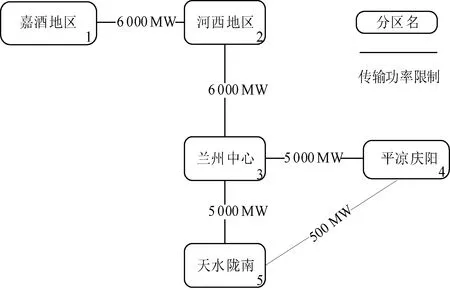
图3 甘肃电网分区接线图Fig.3 Topology of gird in Gansu

(2)系统负荷。依据国家“十四五”规划，算例中采用乐观估计对甘肃省未来电力需求进行预测，预计2028年系统最大负荷将达到29 105 MW。

(3)系统装机。算例中火电装机采用保守估计，新能源采用乐观估计进行预测，省内水电多为不可调节小水电，新能源置信容量采用文献[20,21]的方法。预计2028年全省装机共计78 700 MW，其中，火电装机25 000 MW，风电装机24 450 MW，光伏装机15 550 MW，储能4 000 MW，水电9 700 MW。

4.2 算例分析

算例采用甘肃省电力系统数据对所提出的模型进行验证。市场中各发电商报价详情见表1。市场报价考虑13家火电发电企业共计29台机组报价，申报容量25 000 MW，机组强迫停运率为2019年实际统计数据，新建机组按同容量等效。同时，算例考虑了在新能源装机容量最大的嘉酒地区和负荷最高的兰州中心地区新建6家储能电站，装机容量6 000 MW/24 000 MW·h，由式(4)和式(5)核定可申报有效容量共计4 000 MW/16 000 MW·h。

表1 机组报价数据Tab.1 Date of capacity offers

将可靠性标准设定为LOLE≤3 h/y,并将上述数据代入所提出的模型中进行计算。

IRM计算结果见表2，可以看出求解结果为最佳IRM值0.139 5，即静态装机容量为最大负荷的113.95%，此时对应的系统可靠性指标LOLE为2.994 h/y，符合设定的可靠性标准。表2中展示的迭代过程可以直观显示求解过程中对于可靠性和经济性的优化过程，当达到容量上限值时，可靠性指标为0.619 h/y，系统可靠性非常高，容量足够充裕；同理当达到容量下限值时，可靠性指标为16.922 h/y，系统可靠性不足，此时容量供应相当紧张。

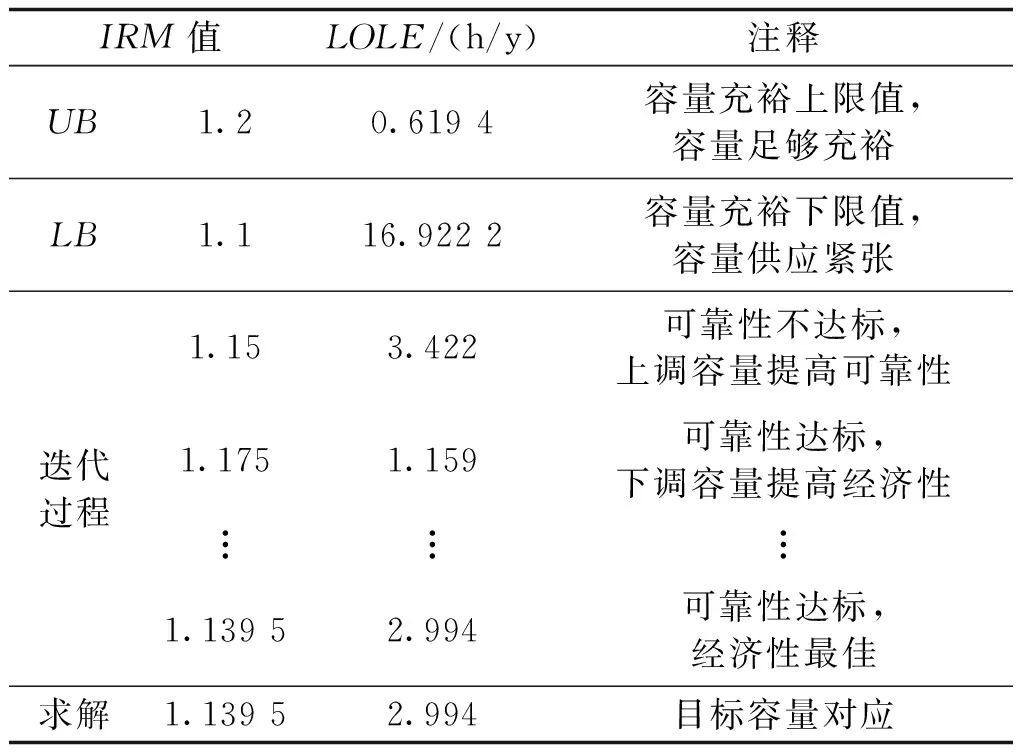
表2 IRM计算过程Tab.2 IRM calculation process

(1)市场出清结果

从市场出清结果来看，表3中全区共计出清有效容量31 268 MW,即装机容量66 930 MW。其中优先出清风电有效容量3 668 MW(装机24 450 MW)，光伏有效容量3 100 MW(装机15 500 MW)。火电机组出清22台，有效容量共计20 500 MW，储能电站出清有效容量4 000 MW。系统出清价格为115 元/(kW·y)，即全系统可以在2028年以115元/(kW·y)的价格获得66 930 MW的发电容量，所中标的机组需在2028年承诺期内提供中标的容量。

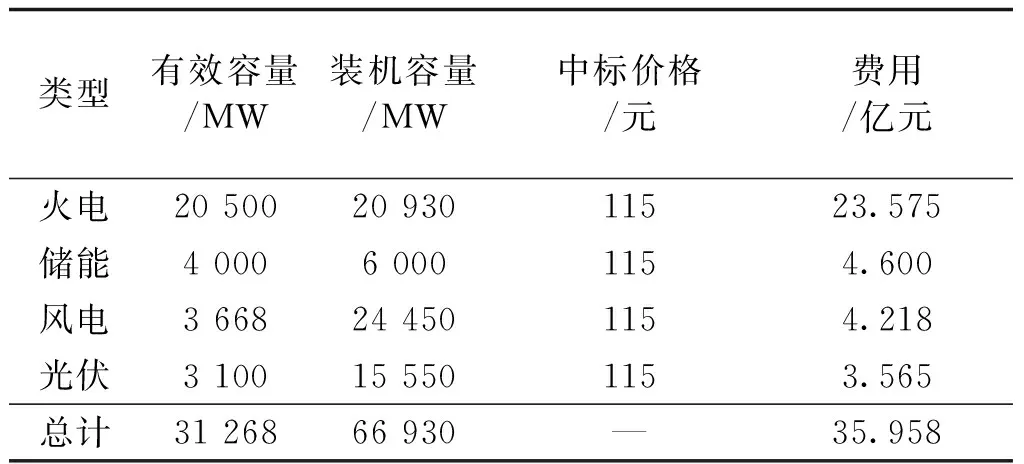
表3 市场出清结果Tab.3 Capacity market cleared results

系统内容量采购费用共计35.958亿元，其中火电23.575亿元，储能4.6亿元，新能源7.783亿元。从发电侧来看，对比国家能源局公布的“十二五”火电造价结算数据3 746元/kW，以机组服役20年计，发电厂可以从容量市场回收大约60%的固定成本；从用户侧看，结合预测的年度用电量2 105亿kW·h，度电容量电价0.017元。这不是在能量电价上的附加电价，容量市场的获利会使机组在能量市场和辅助服务市场降低报价，从而平抑能量市场电价波动，从长期时间尺度上降低用能成本。

各分区有效容量出清结果见表4，装机容量如图4所示，从有效容量来看，新能源资源丰富的嘉酒地区出清火电3 500 MW，储能2 000 MW，新能源3 737 MW。兰州地区是全省负荷中心，出清火电9 530 MW，储能1 500 MW，总装机容量也最大，各类电源类型比较均衡。

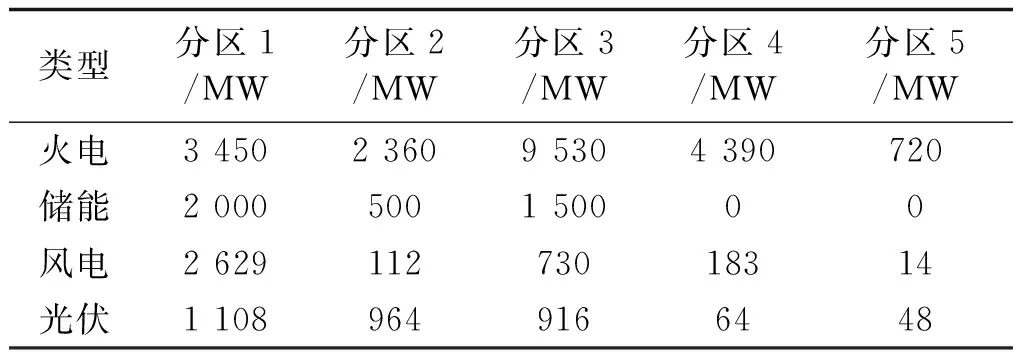
表4 各分区有效容量出清结果Tab.4 Result of each district

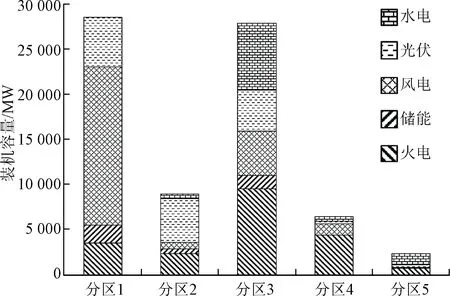
图4 各分区装机结构Fig.4 Capacity structure of each district

图5给出了计算结果中的有效容量传输示意图，可以看出，5个容量市场分区中，兰州中心、河西地区及天水陇南地区为容量输入地区，嘉酒地区和平凉庆阳地区为容量输出地区。全省来看容量从装机较大分区流向负荷较大的兰州中心分区，符合全局最优的目标。

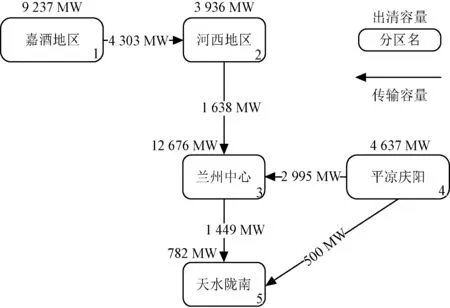
图5 容量传输Fig.5 Capacity transmission

(2)不同储能容量情景

模型中将储能纳入了容量市场，同时在系统可靠性约束中加入了储能运行约束，因此不同容量的储能参与市场对出清结果影响各异。

表5给出了三种不同情景下的市场出清结果，在无储能参与情况下市场出清容量30 761 MW，出清价格117元，容量采购成本共计35.99亿元；情景1中，当4家储能电站参与市场时，市场出清容量共计30 905 MW，出清价格116.5元，市场费用总计36.004亿元，市场采购费用上升，这是由于模型中可靠性约束计及了储能的运行约束，使其相对于同容量的传统机组对可靠性的贡献较低。采购容量上升这一现象在更多储能参与的情景2中体现的更为明显，系统共计出清容量31 268 MW，相较于无储能参与的情景增加了363 MW，但市场总费用降低了461万元，这是由于市场模拟时一般认为储能报价要低于传统机组[13]，更多储能的参与使得统一出清的边际电价更低，从而降低了市场成本，因此适当规模的储能可以降低容量市场成本。

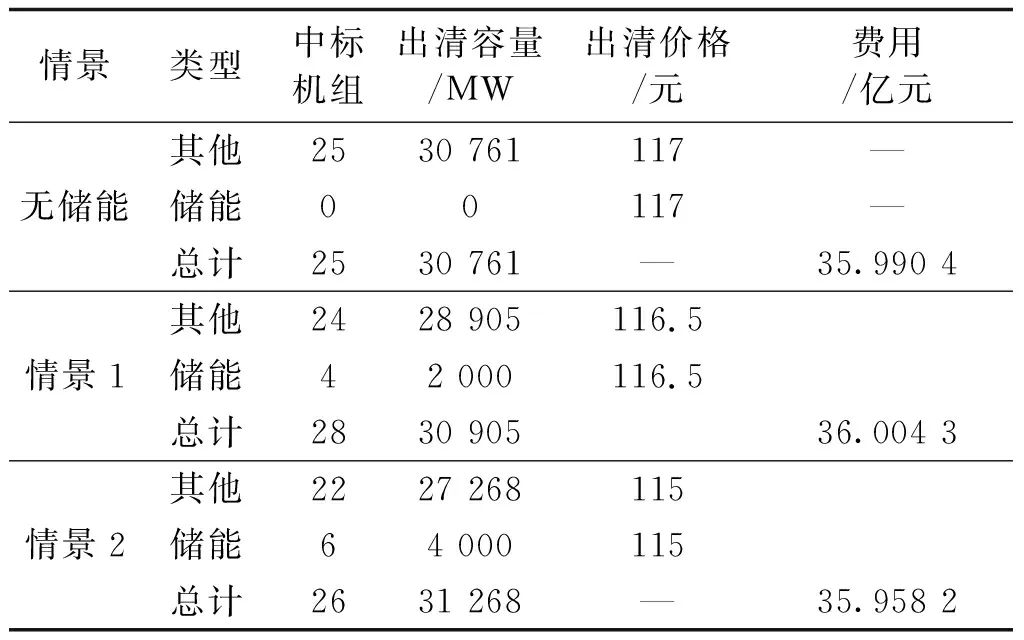
表5 不同储能下出清结果Tab.5 Variation of cleaning result respect to energy storage

当更大规模的储能参与时，如图6所示，由于可靠性的约束会使得市场出清容量快速增长，使市场经济性降低，容量费用大幅度上升。

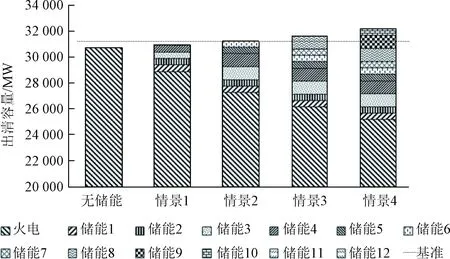
图6 不同储能情景下市场出清结果Fig.6 Variation of cleaning result respect to energy storage

(3)不同容量新能源装机情景

所建模型中新能源以置信容量作为有效容量参与市场并优先出清，在可靠性评估时计及新能源出力的波动性。前述算例中新能源装机40 000 MW，占比49.3%，假设新能源装机不断增大，负荷及网架等其他条件不变，对模拟运行年不同新能源占比对市场影响进行分析。结果见表6，可以看出随着新能源装机从40 000 MW增加到45 000 MW，火电及储能机组的出清容量从24 500 MW降低至24 026 MW，市场出清容量从31 268 MW增长到31 790 MW，相应的市场费用由35.958亿元上升至36.081亿元，增加了1 230万元。但考虑到新能源装机容量占比增大后，由于其发电成本较小，因此能量市场价格会显著下降，总体用电成本不会大幅度上涨。同时需要注意到出清装机容量由76 200 MW增加到80 876 MW，即新能源装机新增5 000 MW，为保持系统可靠性指标，火电和储能机组只减少了324 MW，这是由新能源的置信容量较低造成的。

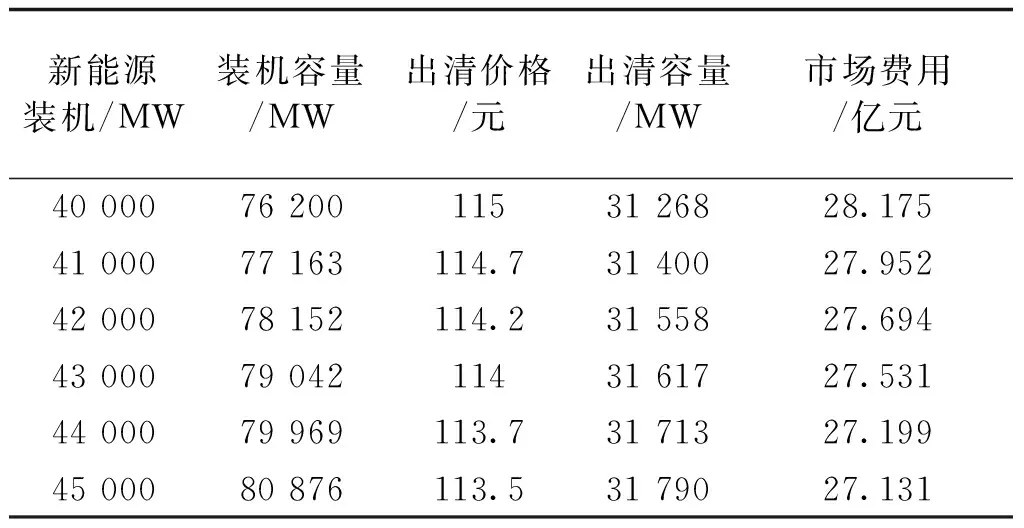
表6 不同新能源装机下出清结果Tab.6 Variation of cleaning result respect to renewable energy

5 结论

本文提出了一种面向高比例新能源电力系统的容量市场出清模型，所提出的模型纳入了新能源并优先出清，以置信容量作为有效容量，肯定了新能源的容量价值，有利于新型电力系统的构建。此外模型引入储能参与市场，储能的加入有利于高比例新能源渗透情况下电力系统中新能源的消纳，但同时由于可靠性的约束，大量储能的加入可能会提高市场成本。同时考虑到高比例新能源渗透下系统的可靠性问题，模型加入了可靠性约束，并通过迭代寻优使市场以最小的成本获取足够的发电容量，保障系统可靠性和经济性兼顾。此外，所提出的模型还可以增加其他能源形式或者用于电源结构的规划。