汽车轮渡智能装载优化方案研究

陈 朴, 方景芳, 刘 军, 陈家伟

(兰州理工大学 机电工程学院, 甘肃 兰州 730050)

汽车轮渡作为城市立体交通系统的一部分，有着不可或缺的作用.传统汽车渡船的装载过程，由渡口安全员和渡船驾驶员共同完成.船只的载重与平衡等实况，通过仪器显示，由驾驶员控制.安全员通过无线电传呼机通报待渡船只的剩余容量、装载进展等信息，人工安排车辆的上船次序.这种半人工的汽渡装载过程，往往持续时间较长，无法充分利用船只的运载能力且效率低下，智能化程度亟待提高.如何实现汽渡船装载过程的智能化尚未见相关研究，但国内外已有诸多一般船舶装载研究，可作借鉴.

Le Carrer等[1]为优化潮汐港口和浅海的船舶装载设计了一个计算货物装载和调度决策的航运决策模型，采用粒子群优化和蒙特卡罗模拟求解航运净收益约束优化问题.Azevedo等[2]以最优化船舶稳性和最小化倒箱操作为目标，以加权形式，结合基于规则的方式，采用智能搜索算法对三维集装箱配载问题进行求解，并给出具体算例验证了算法的有效性.Daniela等[3]针对挂靠多港口集装箱船的智能化配载问题，提出了一种MIP(混合整数规划)模型.Parreo等[4]提出一种贪婪随机自适应搜索算法，比经典整数规划算法更具多样性，能产生较多优异解.Zhang等[5]以倒箱量和船舶稳性为目标，利用启发式算法和多目标遗传算法，并采用贪婪搜索策略从理论上解决了船舶的配载问题.Jo等[6]针对三维集装箱配载优化问题，以稳性和倒箱量为目标，提出一种Pareto聚类搜索算法，能产生较好的非劣解集.Wu等[7]以集装箱船装载过程为背景，分析了影响装载的因素，为集装箱装载系统的建设提供了可靠思路.Khoirun等[8]研究了水泥公司卸船负荷，使用混合整数线性规划求解方法以最小化总运输成本.Wen等[9]为制定最小化所需船舶货舱数量的预制产品装载计划，建立整数规划模型，设计启发式算法来获得高质量的解决方案.

李虎等[10]以船舶舱容限制、允许重量和货物堆装规则为约束条件,构造了一种混合遗传算法来解决散货船配载问题,以提高仓容利用率和装载效率.朱莹等[11]建立了集装箱船装载的数学模型，提出了一种新型混合遗传智能算法，算法中设计了包含货物装填顺序和放置状态的两段编码方式.朱莹等[12]还以船舱空间利用率最大为目标，建立杂货船装载问题的数学模型，提出了一种结合启发式算法和遗传算法的混合遗传算法，并验证了算法的正确性.汪达钦等[13]在船舶配载0/1规划模型中，将港机在各船舱的作业分配作为决策变量,以最短装船时间为目标,联合优化船舶配载和港机分配问题,从而实现了出厂物流的整体优化.田浩[14]考虑了集装箱船舶各个液舱中装载量及自由液面对集装箱船配载的影响，使用遗传算法对集装箱船舶配载问题进行求解.方晟等[15]根据散货船使用多装船机的装载作业情况,建立了散货船智能装载数学模型,使用多目标遗传算法求解,得到优化后的Pareto解集.

纵观国内外研究现状，船舶装载问题的研究对象多为集装箱船和散货船，关于汽渡船装载的研究几乎没有.汽车不同于货物，汽渡装载方式也不同于集装箱船和散货船.本文建立了汽渡装载模型，利用汽渡装载算法求解，并设计了汽渡智能装载系统以智能化装载模式替代传统的人工装载模式，结合G公司实际案例，提高了汽渡公司的经济效益，具有一定的现实意义.

1 汽渡渡运流程分析

一般在汽渡渡运过程中，到达车辆首先经过过磅区称重，然后进入渡口收费站，收费站根据车辆的重量和类型收取渡江费用，当待渡车辆总重量接近渡船安全载重，即暂停收费，待渡车辆进入等待区.在渡口安全员的指挥下，待渡车辆依序上船准备渡江，当待渡车辆由于甲板面积限制无法驶入甲板时结束装载，渡船执行渡江任务，未能装载的车辆停留在待渡区等待下一艘渡船装载.并以此循环，其渡运流程如图1所示.

图1 渡运流程图Fig.1 Ferry flow chart

通过分析，可知渡运流程主要有以下几个特点：

(1) 渡船装载时，待渡车辆与甲板边缘以及待渡车辆间均需留出一定的空间.

(2) 渡船装载时，车辆不能够堆叠摆放，只能平面二维装载；车辆停放的方向应顺应上下船方向.

(3) 渡船的卸载，采用FIFO原则，即先进先出原则.

(4) 由于渡船的渡运成本主要与船舶自身的吨位和航行距离有关，渡船的装载量对成本影响较小，故装载量越高收益越高.

通过分析原渡运流程和装载特点，本文的主要工作如下：

(1) 车辆过磅得到车辆的重量和类型信息，使进入等待区的车辆重量尽量接近且小于当次渡运船舶的最大载重.

(2) 在等待区设图像识别参照杆,并在正上方安装摄像头对所有等待区车辆拍照，进行图像识别得到每辆车的长、宽信息，最后通过汽渡装载系统内设计的汽渡智能装载算法得到智能装载方案，同时使企业的渡运收益最高，如图2所示.

图2 汽渡智能装载示意图Fig.2 Schematic diagram of intelligent loading of automobile ferry

2 汽车轮渡装载模型

2.1 模型假设

为便于模型的建立，假设：汽渡的渡运成本与车辆装载的多少无关；在保证安全的前提下，渡船一次装载车辆的总票价越高，渡口的效益越高；汽渡船装载不允许车辆堆叠放置，其装载情况不同于散货船或集装箱货船的装载，在本模型中车辆不可旋转且装载顺序设定为自右向左，自上而下；所有车辆在等待过程中均不会中途离队；装载时，不同于集装箱船装载时各集装箱之间可以紧靠，汽渡装载时车辆与车辆之间必须保证的空隙为安全车距2d0，车辆与渡船首、尾和两侧之间的空隙均为d0，且待渡车辆不会发生碰撞等特殊情况.为防止出现二次等待，规定如上次到达车辆未进入等待区则下一次必须进入.

本文建模设计参数包括：到达车辆集合D，包含m辆车；dj=(wj,pj)，j=1,2,…,n，wj为第j辆车的重量,pj为第j辆车的票价；等待区车辆集合为C，且D⊇C，包含n辆车且n≤m;ci=(li,fi,wi,pi)，i=1,2,…,n，li为车辆i的长度,fi为车辆i的宽度,wi为车辆i的重量，pi为车辆i的票价；W为渡船的定额吨位；L为渡船的甲板长度；F为渡船甲板宽度；d0为装载时保留的空隙长度，2d0为安全车距；ai为车ci最右侧与甲板右边缘之间的距离;bi为车ci最上侧与甲板上边缘之间的距离；xi为决策变量，表示车辆ci是否装上甲板；yj为决策变量，表示车辆dj是否进入等待区；xi和yj的具体含义如下：

2.2 模型构建

本模型考虑如下因素：结合渡船的自重和吃水情况与单个待渡车辆的重量，重量约束将有效限制渡船装载待渡车辆的总数量；汽渡船配备有相应的平衡重装置，故渡船的平衡性对车辆装载的影响很小；渡船在江面航行，风力的影响较小；汽渡船只有在江面能见度达标时才可航行等.因此，本汽渡装载模型类似于二维装箱问题，是典型的组合优化问题，其中目标函数设定为单次渡运收益最高，约束条件为重量约束和面积约束.

目标函数：

(3)

约束条件：

其中：式(3)为模型目标函数，即使渡船装载车辆的总收益最高；式(4，5)表示重量约束，即等待区和装载车辆的总重量均不超过渡船的定额吨位；式(6,7)表示尺寸约束中每辆车的长、宽加上前后、左右的安全车距和不可超过甲板的长和宽；式(8)表示装载时车辆不可与其他车辆及甲板边缘重合；式(9)表示面积约束，即装载车辆总面积不超过甲板面积；式(10)表示变量li、fi为正数，且ai、bi必须不小于装载时保留的空隙长度d0.

3 算法设计

汽渡船的智能装载问题可分解为两部分，首先是筛选进入等待区的车辆，使其在不超重的前提下总收入最高，该部分的求解与背包问题类似；其次，由于渡船装载不允许车辆堆叠放置，也不可旋转，故等待区车辆装载问题可简化为二维装箱问题，用BL算法求解.等待区装载上渡船甲板的车辆越多，装载率越高.故结合背包问题算法和BL算法，设计启发式算法求解在重量和面积约束下，某航次渡船的最佳车辆装载方案，进而求得最高收益和对应的装载率.算法求解步骤如下：

步骤1：将上次到达但未进入等待区车辆设为最优先进入等待区.输入过磅处测得的本次到达车辆票价和重量，判断进入等待区的车辆总重量是否小于渡船安全载重，若是则全部进入等待区，执行步骤4，否则执行步骤2.

步骤2：将本次到达车辆的单位重量收益存储到pvalue，并按照单位重量收益降序排列于上次到达但未进入等待区车辆之后.

步骤3：将车辆按照步骤2中顺序依次进入等待区，计算已进入等待区车辆总重量，当总重量超过渡船安全载重时停止车辆进入，执行步骤4.

步骤4：将等待区车辆根据进入顺序排序并编号，同时图像识别后得到每辆车的长宽信息.

步骤5：随机放置ci至紧靠甲板右上角,将ci尽可能向下移动,再将ci尽可能向左移动,直到ci不能再向下向左移动为止.判断过程中是否与其他车辆或甲板边缘有重合，若是则不将ci装船，令xi=0,i=i+1,i=1,2,…,n，否则将ci装船执行步骤6.

步骤6：令xi=1，记录所有能装下(xi=1)的车辆编号，输出装载结果.

4 算例分析

以G汽渡公司为例，G公司主要承担G市和P市的汽车渡运任务，现有三条航线，主力渡运船10只，船型均为对称的，双头、单体、单甲板、舯桥楼式，但其甲板长宽和定额吨位各不相同.以航线1为例，服务于该航线的为渡船1、2、3.渡船1的定额吨位W1为150 t,甲板长度和宽度为40 m和13 m;渡船2的W2为220 t，甲板长度和宽度为50 m和15 m;渡船3的W3为190 t，甲板长度和宽度为45 m和13 m.

本文首先选取G公司某年某日航线1航次5的待渡车辆情况.该航次渡船1、3从北岸出发，渡船2从南岸出发；两岸到达车辆共96辆，其中客车67辆，货车29辆，票价根据G汽渡有限公司渡运收费标准计算，由车辆类型等决定；重量数据在过磅时测得，原装载方案的装载率等数据为G公司历史数据.本文设计汽渡智能装载算法并计算，结合渡船1数据得到第一批进入南岸等待区车辆，对比原方案和智能装载方案等待区车辆的数据，如表1所列.

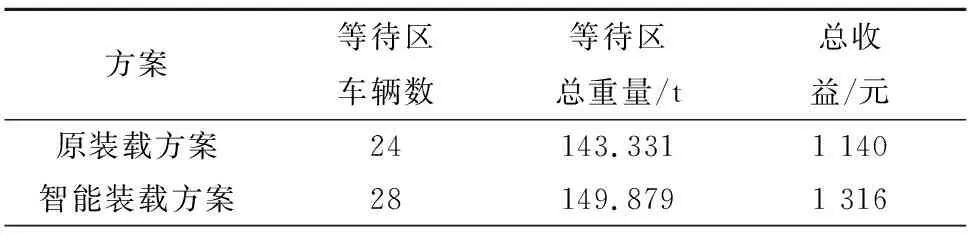
表1 等待区车辆数据对比Tab.1 Comparison of vehicle data in waiting area

通过图像识别得到等待区车辆长宽信息，设计汽渡装载算法并计算，得到等待区装上渡船1甲板的车辆及其停放方案，安全车距d0设定为0.4 m，迭代100次，算法寻优的收益最大值为958元，装载车辆数为21辆，如图3所示.而原装载方案的单次渡运收益为763元，装载车辆数为17辆.船舶装载率(船舶载重量利用率)的公式如下：

(11)

求得最佳装载方案的装载率为70.42%，而原装载方案的装载率为61.34%.

在汽渡装载算法的基础上设计汽渡船智能装载系统，运行界面如图4所示.当1号渡船靠岸后，将等待区车辆信息输入即可得到最佳装载车辆停放图、应载车辆数和装载率.

图4 系统运行界面Fig.4 System operation interface

对该航线其他汽渡船使用智能装载方案优化后对比，如表2所列.使用IBM SPSS 19对结果进行配对样本t检验(见表3～5).

表2 装载方案对比Tab.2 Comparison of loading schemes

表3 成对样本统计量Tab.3 Paired sample statistics

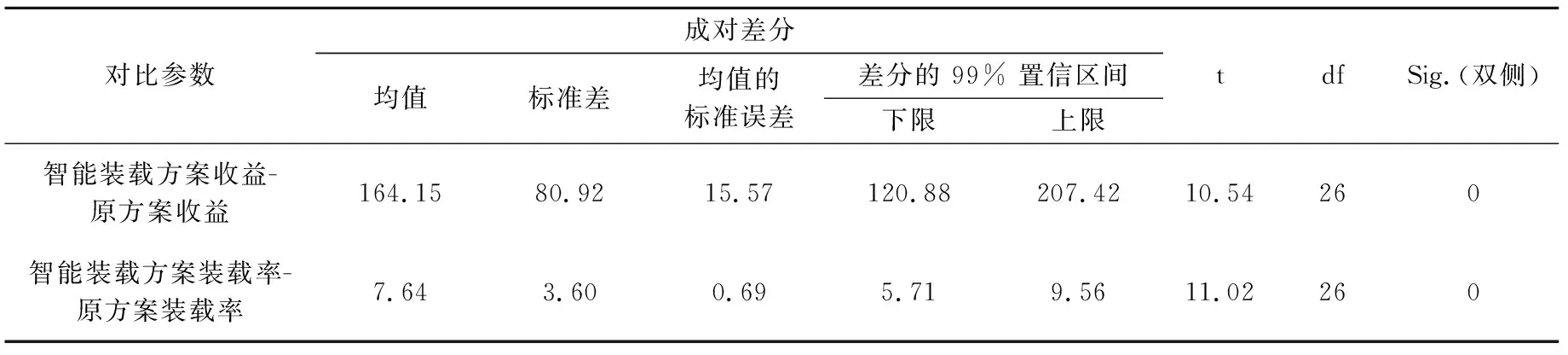
表4 成对样本检验Tab.4 Paired sample test

表5 成对样本相关系数Tab.5 Paired sample correlation coefficient

由表2可知，在该航线上本文设计的智能装载方案比原装载方案装载率平均提高了7.64%，收益也平均提高了16.64%，表4中的sig=0.00<0.05，表明收益和装载率前后都有显著变化.最后，对比G公司某年所有航线历史数据和大规模使用智能装载方案优化后结果(表6)，优化后比优化前提高了7.46%的装载率，提高了15.7%的收益.

表6 大规模优化结果Tab.6 Large scale optimization results

5 结论

本文深入研究汽车渡船装载现状，结合G汽渡公司的原渡运流程进行分析，设计了一套基于启发式算法的智能装载流程优化方案.实际运用结果表明,本文提出的智能装载方案和算法能比原方案获得更好效益.应用此方案装载率提高了7.46%，G公司日平均收益提高了30 279.64元.优化后的方案不仅可以减少甲板面积的浪费，增加汽渡公司总收益，还能提高装载率，减少待渡车辆等待时间.设计的渡船装载系统可应用于汽渡船舶装载，能够有效降低安全员的工作强度，避免反复的人工确认，使汽渡装载的智能化程度大大提高.