基于本量利分析模型的高校财务核算管理*

贾 滨杨保良王 康

1.亳州学院 安徽 亳州；2.淮南师范学院 安徽 淮南

一、引言

本量利分析法（CVP分析法）起源于20世纪20年代的西方国家，作为财务管理中的基本决策分析方法之一，其核心是在成本性态的分析基础上对成本 业务量 利润三者的筹划，以期获得盈亏平衡点，并根据盈亏平衡点做出最佳财务决策。

我国高等教育持续快速发展，高校为满足国家基本办学条件要求，不断进行负债扩建，《2006年：中国社会形势分析与预测》社会蓝皮书称，2005年我国高校向银行贷款总量约在1500亿至2000亿元之间。据有关部门统计，截至2021年年底，我国高校负债总量已经远远超过这个数字且增长势头不减。同时，普通高校报考人数开始减少，面对越来越激烈的竞争，各高校不得不采取措施，节约经费，提高办学效益。本文将运用本量利分析原理，对加强高校财务管理、确定合理办学规模、提高办学效益，提出建议。

二、研究假设与模型构建

1.研究假设

本量利分析目前常用于营利性组织，其核心是在变动成本的基础上对成本-业务量-利润三者的筹划，以期获得盈亏平衡点，并根据盈亏平衡点做出最佳财务决策。

（1）假设前提。首先，在实际经济生活中，成本、业务量、利润三者之间并不是简单的线性关系，其受多方面因素影响。其次，由于经济业务不同、成本计量属性存在差异，导致对成本的分类界限存在分歧。最后，在实际生活中企业产品往往具有多样性且在某一时期内很难量化其是否达到产销平衡。基于以上前提，本文对本量利模型做出以下假设。

H1：线性关系假设。假设在一定时期内，商品销售价格、单位成本均保持不变，这样可以保证销售收入、变动成本与销售数量呈线性关系，成本、业务量、利润三者之间也能保持线性关系。

H2：成本分类假设。假设严格按照成本性态对成本进行分类。

H3：产销平衡假设。假设企业生产出来的商品总是可以顺利售出。

（2）基本公式。利润总额=收入总额-成本总额=收入总额-变动成本总额-固定成本总额=单价×业务量-单位变动成本×业务量-固定成本总额。

数学模型为TP=px bx a，其中TP代表企业追求的利润总额；p代表单价；b代表单位变动成本；x代表业务量；a代表固定成本总额。

2.模型构建

高校属于非营利性组织，其追求的并非仅是利润的最大化，而是在公益性、社会价值与营利性之间找到最佳平衡点，围绕此平衡点展开一系列指标计算与分析，从而使高校获得持续健康发展。综合多方面因素的考虑，本文认为高校追求的目标利润可以用事业结余（TP）表示；单价（p）可以用纵向事业经费、学杂费、培训费等生均教育收入表示；单位变动成本（b）可以用生均教育支出表示；业务量（x）可以用在校学生数量表示；固定成本总额（a）可以用教职工工资，教学楼、实验器材等不动产折旧费表示。此外，考虑到高校横向经费收入因素，本文认为高校本量利模型还应加入固定收入，用i表示（取高校近三年横向经费收入均值），各变量具体含义如表1所示。

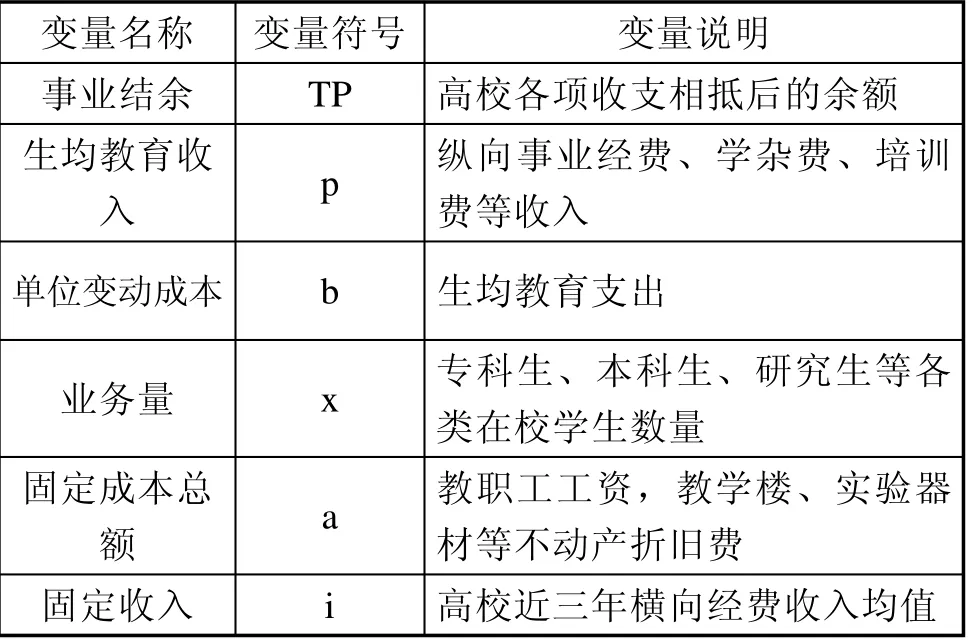
表1 变量含义

调整后的高校财务管理本量利模型为：

事业结余=收入总额 变动成本总额 固定成本总额+固定收入，数学模型为TP=px bx a+i。

三、本量利分析在高校中的具体应用

1.本量利分析实施原理

进行本量利分析，首先要确定盈亏平衡点，盈亏平衡点是一种动态平衡，是指销售收入与变动成本之差与固定成本持平的状态，对其进行分析需要借助边际贡献法和保本图法，边际贡献法（M arginalContribution）是指售价考虑了减去变动成本后的差额再补偿固定成本后所获得收益的定价方法，公式表示为m c=p b或者m cx=px bx。保本图又称盈亏平衡图，以横轴表示产品销售量（或销售收入）；纵轴表示销售成本和销售收入；销售收入线和销售成本线交叉之处为保本点。借助边际贡献法和保本图法可以更加清晰明了地观察到盈亏平衡点并分析其走势。

2.本量利分析实施目的

本量利分析被企业应用的目的是找出盈亏平衡点以便做出最佳财务决策，用最小的成本获取最大的利润。高校作为一个公益性组织，盈利不是最终目的，但借助本量利分析模型可以为其确定盈亏平衡点，继而确定最佳招生数量，维持高校持续健康运转，从而减少财政负担。

3.盈亏平衡点的确定

企业中确定盈亏平衡点就是令利润等于零的那一点，即：TP=0,也即：px bx a=0，（p>b）。

解得：x0=a/(p b)，根据x0可以推出销售收入（y1）和总成本（y2）的表达方式：

根据上述公式绘制出企业盈亏平衡图如图1所示。

从图1可以明显看出企业达到盈亏平衡时，总收入与总成本相等，此刻，边际贡献刚好可以补偿固定成本总额。

图1 企业盈亏平衡图

根据调整后的高校财务管理本量利模型：TP=px bx a+i，我们可以确定高校盈亏平衡点，令TP=px bx a+i=0

解得：x1=（a i）/（p b），根据x1可以推出销售收入（y1）和总成本（y2）的表达方式：

对于x1=（a i）/（p b），我们需要进行分类讨论：

①当a>i且p>b时，绘制高校盈亏平衡图如图2所示。

图2 高校盈亏平衡图

从图2中可以看出，当高校总收入与总成本相同时，即实现盈亏平衡，此时，边际贡献刚好可以弥补固定成本与固定收入之差。换言之，在其他条件相同时，在这一点的招生人数（x1）是保证不亏损的最低人数，超过这一点的招生人数，即高校可实现盈利的人数（事业结余）。

②当a

图3 高校盈亏平衡图

从图3中可以看出，当高校总收入与总成本相同时，即达到盈亏平衡。此时，应引起注意的是，边际贡献是负数，即随着学生招收数量的增加，高校收入不但没有增加，反而在持续减少，这显然与实际情况不符，因此，对于这种缺乏实际研究意义的模型我们将不再讨论。

4.盈亏平衡分析在高校决策中的具体应用

资料1：假设W高校2021年各类在校学生为5600人，2021年全年纵向事业经费、学杂费、培训费等变动收入共计18 000元/人，近三年平均横向经费为203 000元，教职工工资、教学楼、实验器材等不动产折旧总额为31 032 760元，生均教育支出为12 865元/人，试分析W大学是否需要扩招？如需要扩招，应扩招多少人？

分析：由资料可知，x=5600，p=18 000，i=203 000，a=31 032 760，b=12 865。满足a>i且p>b，符合高校盈亏平衡计算条件。根据调整后的高校财务本量利模型：TP=px bx a+i，可知要分析W大学是否需要扩招，首先要确定最佳招生人数，需要满足TP=0，即px bx a+i=0，将p=18 000,b=12 865，a=31 032 760，i=203 000代入模型可得18 000x 12 865x 31 032 760+203 000=0

解得：x=6004人，由于6004>5600，因此，W高校需要扩招，至少应再扩招404人（6004 5600）。

四、高校本量利模型的敏感性分析

高校本量利模型的核心是在变动成本的基础上对办学成本—学生数量—事业结余三者的筹划，以期获得盈亏平衡点，并根据盈亏平衡点做出最佳招生政策。考虑到高校招生的政策性变化，需要对每个参数进行敏感性分析，以确保单个参数变化时不致使出现由盈转亏的现象。

在高校本量利模型中，影响事业结余的因素主要有生均教育收入（p）、生均教育支出（b）、学生数量（x）和固定成本总额（a）。高校本量利敏感性分析就是分析在现有基础上有关参数的变化对事业结余的影响，以及该参数变化在多大范围内会导致事业结余由盈利变为亏损。通过敏感性分析可以知道哪些参数对事业结余比较敏感，哪些参数对事业结余不太敏感。

资料2：假设W高校2021年各类在校学生为7000人，其他同资料1（2021年全年纵向事业经费、学杂费、培训费等变动收入共计18000元/人，近三年平均横向经费为203 000元，教职工工资、教学楼、实验器材等不动产折旧总额为31032760元，生均教育支出为12865元/人）。

经分析可知2021年W高校事业结余为：TP=（18000 12865）×7000 31032760+203000=5115240元。

1.生均教育收入的敏感性分析

假设资料2中生均教育收入提高10%，即p1=18 000×（1+10%）=19 800元；事业结余TP1=（19 800 12 865）×7000 31 032 760+203 000=17 715 240元；

事业结余变化率=12 600 000/5 115 240×100%=246%；生均教育收入的敏感系数=246%/10%=24.6。

由计算结果可知，生均教育收入对事业结余的敏感程度较高，在其他条件不变的情况下，当生均教育收入提高1%，事业结余就随之提高24.6%，反之亦然。

2.生均教育支出的敏感性分析

假设资料2中生均教育支出提高10%，即b2=12865×（1+10%）=14 151.5元；

事业结余TP2=（18000 14151.5）×7000 31032760+203 000= 3 890 260元；

事业结余变化率= 9 005 500/5 115 240×100%=176%；生均教育支出的敏感系数= 176%/10%=17.6。

由计算结果可知，生均教育支出与事业结余呈反向关系变化，当生均教育支出提高1%，事业结余就下降17.6%，反之亦然。

3.学生数量的敏感性分析

假设资料2中学生数量提高10%，即x3=7000×（1+10%）=7700人；

事业结余TP3=（18 000 12 865）×7700 31 032 760+203 000=8 709 740元；

事业结余变化率=3 594 500/5 115 240×100%=70%；学生数量的敏感系数=70%/10%=7。

由计算结果可知，事业结余对学生数量的依赖程度较低且呈正相关关系，当学生数量提高1%，事业结余就提高7%，反之亦然。

五、结语

综上分析，可以得出以下结论：第一，在变动成本的基础上对办学成本—学生数量—事业结余三者筹划，获得盈亏平衡点，根据盈亏平衡点可以制定最佳招生政策和本单位的会计制度。第二，根据本量利分析模型，应当适量引进纵向经费，提升教育和科研质量，从而减少财政压力。总之，本量利分析模型对于高校财务核算管理的发展、财务管理制度的健全以及办学内涵的提高有着重要意义。