基于理解，逆向设计觅蹊径——以高一“函数的单调性”复习课为例

刘淑文

（上海市嘉定区第一中学，上海）

随着基础教育课程和教学改革的深入推进，在新课程标准、新教材的“双新”大背景下，教师必须不断地学习和丰富自己的理论知识，适时改变教学模式和方法，将理论应用于实践。基于理解的逆向教学设计以培养学生的核心素养为目标，“以终为始”设计教学活动，为教师的教学实践提供了方法和依据。教师只有在学生真正理解的基础上进行教学设计，以教学目标为导引，确定完成目标的合适的评估证据，设计有效的学习体验和教学，才能让学生把所学的知识迁移到新的环境和挑战中，进而培养学生的核心素养。教学设计应该关注知识之间的整体性，要参照教材和课程标准，研究每一节在每个单元中的作用、在整个高中学习中的作用，将每一节作为一个单元设计的有机组成部分，从单元设计的角度进行整体教学设计，用更有效的学习任务引导学生构建知识体系，巩固知识的同时，层进式提高学生的学习能力。

以下是笔者对高一“函数单调性”复习课的一次逆向设计探究。

【教学设计背景】

单调性的教学是高一第一学期的内容，从具体的一次函数、二次函数等初等函数的学习上升到用符号语言研究函数的性质，将思维从具体引向抽象，从感性上升到理性，这对学生是一个挑战。单调性学习中渗透着数形结合、从特殊到一般、从具体到抽象、从文字语言向符号语言转化等重要思想方法，在函数性质学习中有承上启下的作用，为具体研究幂函数、指数函数、对数函数、三角函数等函数性质以及数列最值问题提供了一般方法和借鉴。从对学生的问卷调查和访谈中了解到，学生在单调性学习中存在概念不清、忽视定义、用特值代替“任意”，利用单调性解决不等式问题时忽略定义域，解决函数性质综合性问题能力弱等情况。因此，教师需要在教学设计中对学生的易错问题、重难点问题加以强化，使学生通过参与课堂实践巩固知识，强化解题方法，在反思和总结中将知识内化，在问题解决中获得成就感，达成学习目标。

【教学设计目标】

《普通高中数学课程标准》和《上海市高中数学学科教学基本要求》对单调性的学习要求是：了解单调性的概念，掌握单调性的基本性质，能利用单调性描绘函数的图象，借助图象，会用符号语言表达单调性，理解单调性的作用和实际意义，会对单调性等基本性质进行研究，掌握研究单调性的一般方法。基于以上要求及学生在单调性问题处理中易犯的错误和存在的困惑，教学设计应该强化对单调性概念的理解，注重单调性的应用，关注单调性与函数其他性质的关联，把握函数的整体性质。同时要渗透数形结合、分类讨论、特殊到一般、具体到抽象、感性到理性等思想方法，提高学生分析问题和解决问题的能力。

【教学设计过程】

在高三的函数单调性复习中，笔者发现，学生对单调性概念及内涵的挖掘不够深刻，习惯于用特殊值代替任意性，往往停留在对教师解法的简单模仿上，方法僵化。反思这种现象，笔者认为单调性的教学需要在高一打好基础、做好铺垫，使学生对单调性的本质有深刻的理解。在本节单调性的复习课上，笔者尝试引入“微资源”，力图帮学生搭建单调性学习的知识网络，深化单调性概念，为函数性质的进一步学习和研究打下基础。

为突破学生在解决单调性问题中出现的思维障碍，本节复习课笔者重点设计了四个板块：（1）热身小练习；（2）单调性概念辨析；（3）判断、证明函数的单调性；（4）单调性的应用。

【板块一】热身小练习

2.若函数y=x2+ax+1在（-∞，2］上单调递减，则实数a的取值范围是a≤-4.

3.若f（x）为奇函数，且在（-∞，0）上是减函数，又f（-2）=0，则x·f（x）＜0的解集为（-∞，-2）∪（2，+∞）.

注：热身小练习是课前设置的实践演练，通过知识点回顾，既可以检测学生的复习效果，也能让学生了解知识的薄弱之处，从而更有针对性地进行课堂学习。

【板块二】单调性概念辨析

函数的单调性反映了函数的变化趋势，是函数的局部性质，为了让学生更好地理解函数概念和本质，笔者设计了如下的“微资源”。

资源1：（1）函数单调性定义：如果函数y=f（x）对于属于定义域I内某个区间上的任意两个自变量的值x1，x2，当x1＜x2时，①都有_______，则称f（x）在这个区间上是增函数，而这个区间称函数的一个_______；②都有_______，则称f（x）在这个区间上是减函数，而这个区间称函数的一个_______.

（2）函数单调性的图象特征：增函数的图象，从左往右看，图象是________；减函数的图象，从左往右看，图象是_________.

注：单调性定义是证明和判断单调性的最基本方法。对定义的回顾，强化了概念意识，为概念的挖掘做好准备；单调性的图象特征，能够帮助学生直观地理解单调性，渗透数形结合的重要思想方法。

资源2：你如何理解函数的单调性？定义中有哪些需要注意的关键字？

注：单调性概念对学生而言较为抽象，了解学生现有的认知水平，可帮助学生从感性认识上升到理性认识，培养学生的抽象思维能力。教师提醒学生关注数学概念的生成过程的同时，还要注意数学概念中语言的严谨性、准确性，培养学生严谨的数学思维品质。

资源3：已知下列命题：

①定义在R上的函数f（x）满足f（2）＞f（1），则函数f（x）是R上的增函数；

②定义在R上的函数f（x）满足f（2）＞f（1），则函数f（x）在R上不是减函数；

③定义在R上的函数f（x）在区间（-∞，0］上是增函数，在区间［0，+∞）上也是增函数，则函数f（x）在R上是增函数；

④定义在R上的函数f（x）在区间（-∞，0］上是增函数，在区间（0，+∞）上也是增函数，则函数f（x）在R上是增函数.

其中正确命题的序号有_______.

注：学生经常会忽略单调性定义中两个自变量选择的任意性，容易犯用特殊值代替一般性的错误。对四个问题的辨析，能够促进学生对单调性本质的理解。

【板块三】如何判断、证明函数的单调性

单调性的判断、证明方法并不唯一，而定义法是最重要和最基本的方法。这一板块笔者从正向和逆向两个方面入手，强调定义法在证明和判断单调性中的重要作用，通过“微资源”为学生搭建知识网络，加强数学基本功训练。

注：本题的设计意图有两个。

1.复习巩固运用定义法判断或证明函数单调性的一般步骤。

（1）设元：在给定区间上任取x1，x2，且x1＜x2；

（2）作差：f（x2）-f（x1）；

（3）变形：对上述差值进行变形（因式分解、配方、或利用不等式的知识）；

（4）判号：判断f（x2）-f（x1）的符号，得出f（x2），f（x1）的大小；

（5）定论：根据定义判断函数f（x）的单调性。

2.所选函数是学生熟悉的反比例函数，便于学生利用数形结合的思想方法分析问题。

注：资源1是正向问题，已知函数的解析式，判断函数的单调性，资源2是逆向问题，已知函数的单调性，确定待定字母的范围。通过正反两个问题的设置，强化解决单调性判断和证明问题的一般方法。正向问题向逆向问题的递进，让学生在体会函数单调性概念本质的同时，也复习了恒成立问题的一般解决方法，将所学知识有机结合，培养数学高阶思维。

【板块四】函数单调性的应用

单调性的应用是单调性学习的难点，能否将学习的知识灵活运用，是检验教学效果、评价学生课堂学习行为的重要依据。这一板块的设计，聚焦教学目标，是对课堂教学达成度的检验证据。

资源1:函数y=x2-2ax在（-∞，1）上是减函数，则实数a的取值范围是_________.

资源2：请你构造一个二次函数，使它在区间［-1，1］上是单调递减__________.

资源3：函数f（x）=ax2+4（a+1）x-3在［2，+∞）上递减，则a的取值范围是__________.

资源4：若函数f（x）为R上的减函数，且f（x）的图象经过点A（0，3）和B（3，-1），则不等式的解集为__________.

A.（-∞，-1）∪（2，+∞） B.（-1，2）

C.（-2，1） D.（-∞，-2）∪（1，+∞）

注：五个“微资源”之间层层递进，由易到难、由具体到抽象,符合学生的认知规律，使学生有“跳一跳就能摘到果子”的感觉，提升学生学习知识的成就感。

【分层作业设计】

（一）基础练习

（Ⅰ）填空题

1.若函数y=f（x）的定义域是R，则“对于任意x∈R，恒有f（x）＜f（x+1）”是“y=f（x）在R上是增函数”的必要非充分条件.

【说明】本题考查学生对单调性概念的掌握，让学生感悟定义中“任意”两字的准确性和严谨性。

2.若函数f（x）=kx2-4x+8在区间［5，20］上单调递减，则实数k的取值范围为

【说明】本题属于易错题，考查学生的分类讨论思想，培养学生思维的严谨性。

【说明】本题是单调性的逆向问题。解决方法通常有两种，一种是变量分离，将函数转化为反比例型函数；另一种是逆用单调性定义，将其转化为恒成立问题。

【说明】本题着重考查学生数形结合和分类讨论的思想方法。

5.若函数f（x），g（x）均为R上增函数，则下列命题中正确的是（2）.

（1）f（x）+g（x）及f（x）g（x）均为增函数；

（2）f（x）+g（x）为增函数，f（x）g（x）单调性无法确定；

（3）f（x）+g（x）单调性无法确定，f（x）g（x）为增函数；

（4）f（x）+g（x）及f（x）g（x）的单调性均无法确定.

【说明】本题需要学生既要会用定义证明正确的命题，也要会举反例证明错误的命题，这类问题常常因为考虑问题不全面而判断错误。

（Ⅱ）选择题

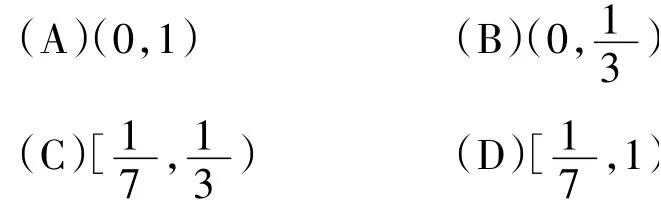
【说明】分段函数的单调性问题是易错和难点问题。学生可借助函数的图象进行数形结合考虑，注意对自变量分界位置函数值大小的比较。

（Ⅲ）解答题

7.已知函数f（x）是奇函数，且f（x）在定义域（-1，1）上递减，若f（1-a）+f（1-a2）＜0，试求实数a的取值范围.

【说明】本题将奇偶性与单调性结合，考查学生综合运用知识的能力，学生的易错点是忽略函数的定义域。

（1）讨论函数f（x）的奇偶性，并说明理由；

（2）若函数f（x）在x∈［2，+∞）上为增函数，求a的取值范围.

【说明】本题综合考查函数的奇偶性和单调性。第（1）题强化解决奇偶性的基本方法，渗透分类讨论的数学思想。第（2）题是单调性问题的逆向考查，强化逆用函数单调性定义，将字母变量分离转化为恒成立问题的思想。在课堂教学和作业设计中要注意对函数综合问题的考查，体现单元设计理念。

（二）拓展练习

9.已知函数f（x）是定义在（0，+∞）上的增函数，且满足f（xy）=f（x）+f（y），f（2）=1，解不等式：f（x）-f（x-2）＞3.

【说明】本题是利用单调性解不等式问题，题目中函数性质以关系式f（xy）=f（x）+f（y）呈现，这种抽象函数问题是难点问题，学生需整合已知条件，分析其内在联系，通过已知不等式建立函数值之间的关系，进而应用单调性解决问题。此类问题注重对学生独立分析问题、解决问题能力的培养，有利于学生将知识内化成能力。

（三）个性化练习

请你结合自己在函数单调性问题中遇到的困难，自己寻找资源，为同学设计一道有关函数单调性的问题。

【说明】个性化作业要求学生为同伴设计作业，一方面可以通过资源搜集强化学生对薄弱知识的掌握，另一方面可以增进同伴之间的合作互助学习，促进共同进步。

【教学设计反思】

通过本课的教学设计实践，笔者更深刻体会到各个年级的数学学习是一个有机整体，知识学习的过程是一个循序渐进的过程。只有在高一、高二打好基础，才能在高三的复习中“厚积薄发”。教育的主体是有生命力、有思考力、有创造力的学生，教师在教育教学中要始终把学生作为主体，在实践中始终关注学生的所思所想，基于理解进行逆向教学设计，从单元教学的角度设计教学，帮助学生打造泛舟数学海洋的双桨，促进学生的终身发展。