有关两个新颖不等式的进一步推广
叶 专, 温志红
(江苏师范大学 数学与统计学院, 徐州 221116)
1 引 言
众所周知,不等式的证明方法非常之多,比如构造法、函数法、分析法、换元法、反证法、设序法、凸凹性法、条件极值法等[1-6],其中,设序法顾名思义就是将变量重新排序,充分利用排序的顺序来证明所需要的不等式.实际上, 利用单调性是证明不等式的常用方法,构造辅助函数简单,通常是将不等式两边直接做差即可.文献[1]利用函数单调性给出了如下一个新颖不等式:
设0≤d≤2,xi>0(i=1,2,…,n),则有
当且仅当x1=x2=…=xn时等号成立.注意, 文献[1]中指出上述不等式中关于d的区间限制0≤d≤2中的上限2是最佳的,不能延拓到比2大的某数使得上述不等式成立.受文献[1]的启发,文献[2]中给出了如上结论的一个对偶形式的结果: 设0≤d≤2,xi>0(i=1,2,…,n),则有
当且仅当x1=x2=…=xn时等号成立.结合设序法与函数法,最近文献[3]将文献[2]所需要的限制条件0≤d≤2放宽到d≥0,即证得如下新颖不等式: 设d≥0,xi>0,(i=1,2,…,n),则有
当且仅当x1=x2=…=xn时等号成立.
2 主要结果
如上几个结果形式简单、结果漂亮、证明简洁,受此启发,本文主要对上述结果进行进一步的推广,即得到如下第一个定理.
定理1设ai>0(i=1,2,…,n)满足
(1)
则对于任意的xi>0(i=1,2,…,n),有
(2)
当且仅当x1=x2=…=xn等号成立.
注 一方面,当n=2时, 条件(1)自然成立, 这表明对于n=2不需要限制条件(1).另一方面, 对于n≥3, 当条件(1)去掉时, 不等式(2)不再成立.比如考虑n=3的情形,选取
不难验证a1,a2,a3不满足条件(1),同时有
这就表明不等式(2)不再成立.注意到当ai=1+(i-1)d(i=1,2,…,n),定理1与文献[3]的结果是一致的, 因此定理1是前人结果的进一步推广.
对于定理1的对偶形式,给出如下定理.
定理2设0 (3) 则对于任意的xi>0(i=1,2,…,n)有 (4) 当且仅当x1=x2=…=xn等号成立. 注 这里需要指出的是当条件(3)去掉时, 不等式(4)不再成立.比如考虑n=2的情形,选取 a1=1,a2=4,x1=10,x2=0.1. 不难验证a1,a2不满足条件(3),同时有 这就表明此时不等式(4)不再成立.注意到当ai=1+(i-1)d(i=1,2,…,n),条件(3)变成 n2min{2,1+d}-[2+(n-1)d]n≥0. 直接计算, 从上式可得d应满足0≤d≤2,这与文献[1]的结果是一致的, 因此定理2是前人结果的进一步推广. (5) 为此,定义一元函数f 对函数f求导数,利用条件(1)可得 这表明f(xkn)在(0,∞)是递增函数.又xk1≤xk2≤…≤xkn, 从而当取xkn=xk1时,有xk1=xk2=…=xkn, 故 综上所述,不等式(5)成立,也就有不等式(2)成立,定理1证明完毕. (6) 事实上, 将矩阵 第二行中xkn+1-i与xkn+1-j(i (aixkn+1-i+ajxkn+1-j)-(aixkn+1-j+ajxkn+1-i)=(ai-aj)(xkn+1-i-xkn+1-j)≤0. (7) 定义一元函数g如下 对函数g求导以及利用定理中的条件可得 这表明g(xkn)在(0,∞)是递增函数.又xk1≤xk2≤…≤xkn, 从而当取xkn=xk1时,有xk1=xk2=…=xkn, 故 综上所述,不等式(7)成立,也就有定理2的结论成立. 本节给出上述两个定理的直接应用. 例1设a1>0,q>0,d≥0, 证明对任意的正整数n,有 证注意到当q=1时, 所需证明的不等式自然成立.为此,只需要证明q>0且q≠1时, 所需证明的不等式成立即可.现在,选取 ai=a1+(i-1)d,xi=x1qi-1,i=1,2,…,n,x1>0. 直接计算可得 这表明条件(1)成立.从而根据定理1有 (8) 简单计算可得 将上述两个估计代入到(8)知 min{x1,x2,…,xn}{(a1-d)(1-q)+d(1-qn)-[a1+(n-1)d](1-q)qn}x1 (9) 注意到当q∈(0,1)时, 有min{x1,x2,…,xn}=xn=x1qn-1, 将其代入到(9)可得 (10) 注意到当q∈(1,∞)时, 有min{x1,x2,…,xn}=x1, 将其代入到(9)可知 (11) 综合(10)和(11), 不难验证 因此, 所需要的结论成立. 于是根据定理2有 将上式整理可得 不同形式的不等式,在理论分析和实际应用中都具有重要作用.文中对已有特殊情形的不等式进行推广,通过对某些参数加以新的特殊限制条件, 得到了两个新颖不等式的更一般的推广结果,并给出了严格的证明和应用举例.对这些不等式进行深入挖掘和多方面思考、逐步深化、循序渐进,有助于培养探索意识和发现能力, 体会运用联系的观点分析问题, 领会从简单到复杂、从表面到本质的科学思维方法.同时, 可以进一步完善和丰富不等式的相关内容. 致谢作者非常感谢相关参考文献对本文的启发及审稿专家提出的宝贵修改意见.3 定理的证明
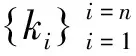
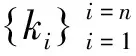
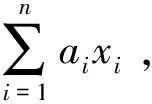
4 应 用
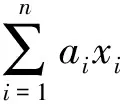
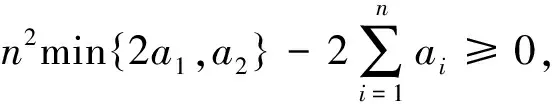
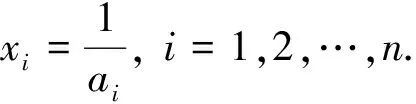
5 结 论

