一类抛物方程解的水平集的曲率估计
赵丽萍, 陈传强
(宁波大学 数学与统计学院,浙江 宁波 315211)
1 引 言
考虑在凸环上建立抛物方程,如下所示
(1)
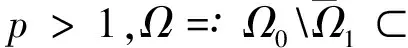
(2)
如果时空水平集{(x,t)∈Ω×(0,T)|u(x,t)=c}对于每一个常数c∈(0,1)都是凸的,那么函数u(x,t)在Ω×(0,T)被称为时空拟凹解.如果(空间)水平集{x∈Ω|u0(x)=c}对于每一个常数c∈(0,1)都凸的,在Ω上的函数u0(x)被叫做是拟凹的.
凸性是偏微分方程的一个基本的几何性质,已经得到了广泛的研究.例如,文献[1]包含一个众所周知的结果,即水平面上单连通凸域上的格林函数为凸Jordan曲线.1956年,文献[2]研究了在3中的极小环,其边界由平行平面P1,P2的两条封闭凸曲线组成,并且在论文中证明了在P1和P2的任意平行平面P都是凸Jordan曲线.1957 年,文献[3]证明了三维有界凸域上格林函数的水平集是严格凸的.1977年,文献[4]将Gabriel的上述结果推广到高维p阶调和函数.文献[5]推广文献[4]结果到非线性椭圆偏微分方程.受到文献[6]结果的启发,文献[7]利用p阶调和函数凸水平集的第二基本形式的常秩定理给出了新的证明.文献[8]关于这个问题还有更多研究(见参考文献[9-12]).
关于椭圆偏微分方程解的水平集的曲率估计也有大量的文献可以参考.对于具有凸水平曲线的二维调和函数和极小曲面,文献[13-15]证明水平曲线的曲率在边界处达到最小值(详细的最新结果参考文献[16]).文献[15]还研究了凸水平曲线的曲率与二维最小曲面高度之间的关系.文献[17]得到了高维调和函数在凸水平集的高斯曲率估计,并且函数包含了边界的高斯曲率和边界上梯度的范数.对于高维主曲率估计,根据边界的主曲率和边界上的梯度范数,文献[18]得到了高维调和函数的严格凸水平集的主曲率下界估计和非线性椭圆方程在一定条件下的界.最近,文献[19]利用了文献[6]提出的常秩定理的方法,得到了一般条件下凸域上完全非线性椭圆方程水平集解的主曲率下界[20].
在文献[21]中, Borell利用布朗运动去研究在u0=0时热方程的时空水平集的某些凸性.后来,文献[22-23]对Borell的定理给出新的证明,并且将其推广到更一般完全非线性椭圆方程抛物拟凹的概念.但他们仍需要初始数据恒等于零,这是一个非常严格的假设.在1995年,文献[24]给出了一类抛物方程解的稳定性与唯一性.文献[25]中研究了水平集的严格凸性并且给出了热方程ut=Δu的时空拟凹解的空间水平集的常秩定理.文献[26-27]中证明了具有初始数据的热方程的强时间拟凹性并且对一般初始数据给出了一些例子.
本文将给出方程(1)解空间水平集的曲率估计,即如下定理.
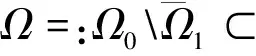
在定理1的证明基础上,还将进一步利用常秩定理,去研究抛物方程解的水平集的曲率估计, 即如下定理.
定理2假设在u∈C3,1(Ω×(0,T))是完全非线性抛物方程(1)的时空拟凹解并且满足(2).那么将会存在一个常数A只依赖于存在对于n,u0,inf|∇u|和‖u‖C2,使得
κu(x,t)≥min{κ0,κ1e-A}eAu(x,t), (x,t)∈Ω×[0,T),
(3)
此时κu(x,t)是空间水平集的Σu(x,t)={y∈Ω|u(y,t)=u(x,t)}的最小主曲率.
注1 定理2可以看作是在文献[19]中定理1.5的抛物版本,同时也是常秩定理的证明过程.更多最新的相关结果可以参考文献[19],[28-29]以及[31-33].
本文的剩余内容安排如下:在第二部分,做一些初步分析;在第三部分,给出定理1的证明;在第四部分,给出定理2的证明.
2 初步分析
在这一部分,将做出一些初步分析.
首先,标记∇u=(u1,…,un)是u的空间梯度,Du=(u1,…,un,ut)是u的时空梯度.
2.1 空间水平集和第二基本形式
假设函数u(x,t)∈C2(Ω×(0,T)),并且对任意固定的(x,t)∈Ω×(0,T)有un≠0.对于空间水平集Σc={x∈Ω|u(x,t)=c}的内法线向量满足
(4)
其中∇u=(u1,u2,…,un-1,un)是u的空间梯度.
函数u在法向(4)的空间水平集的第二基本形式Ⅱ是
(5)
设
则(5)可以表示成
如果Σc={x∈Ω|u(x,t)=c}是局部凸的,就可以知道Σc的第二基本形式在法线方向(4)是半正定的.现假设a(x,t)=(aij(x,t))是Σc={x∈Ω|u(x,t)=c}的Weingarten对称矩阵,由此,可以得到(aij)是半正定的.就如同[11]中计算的那样,若un≠0,那Weingarten 矩阵可以表示成
(6)
其中
上述表示符号中,在点(x,t)处有un(x,t)=|∇u(x,t)|>0,ui(x,t)=0,i=1,…,n-1,aij,k是可交换的,这也就是说它们满足 Codazzi 性质aij,k=aik,j,∀i,j≤n-1.
2.2 时空水平集和第二基本形式
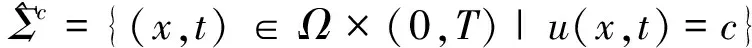
(7)
其中Du=(u1,u2,…,un-1,un,ut)是u的时空梯度.
函数u在法向(8)的时空水平集的第二基本形式Ⅱ是
设
那么,对于上式就可以将其写成
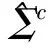
(8)
其中
上述的表示符号中,在点(x,t)处有
ut(x,t)>0,un(x,t)=|∇u(x,t)|>0,ui(x,t)=0,i=1,…,n-1,
由此可以得到
所以
(9)
(10)
(11)
2.3 初等对称函数
在这一部分,将重新回顾在文献[35]中的初等对称函数的定义和一些基本性质.
定义1对于任意k=1,2,…,n,定义
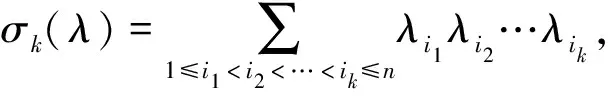
并且有σ0=1并且σk=0对于k>n.
用σk(λ|i)表示λi=0的对称函数且用σk(λ|ij)表示λi=λj=0的对称函数.
易知,初等对称函数有下列性质:
性质1设λ=(λ1,…,λn)∈n对k=0,1,…,n,有
σk(λ)=σk(λ|i)+λiσk-1(λ|i), ∀1≤i≤n,
另外,对矩阵W可以定义σk(W)=σk(λ(W)),其中λ(W)=(λ1(W),λ2(W),…,λn(W))是对称矩阵W的特征值.用σk(W|i)表示除掉i-行和i-列的对称函数以及用σk(W|ij)表示除掉i,j-行和i,j-列的对称函数.然后就有下列的性质.
性质2假设W=(Wij)是对角化的,并且m是正整数,有
(12)
和
(13)
2.4 辅助引理
类似于文献[29]论文中的引理2.5,将给出下列引理
引理1假设对每一个x∈Ω⊂n有W(x)=(Wij(x))N×N≥0,且Wij(x)∈C1,1(Ω),然后对于每一个O⊂⊂Ω,都存在一个只依赖于dist{O,∂Ω}和‖W‖C1,1(Ω)的正数C,使得
(14)
对于每一个x∈O, 1≤i,j≤N.

因为W(x)≥0,所以可选择h(x)=Wii(x)≥0.从上面的论证中得到
(15)
因此(14)对i=j成立.
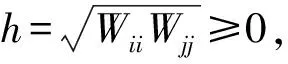
(16)

根据(15)和(16),就可以得到
所以(14)对i≠j成立.
注2 若每一个(x,t)∈Ω×(0,T)有W(x,t)=(Wij(x,t))N×N≥0,且Wij(x,t)∈C1,1(Ω×(0,T)),然后就有对t0 对每一(x,t)∈O×(t0-δ,t0]且1≤i,j≤N,这会有DWij=(∇xWij,∂tWij).如果t0=T,它只成立 对于任一(x,t)∈O×(t0-δ,t0]且1≤i,j≤N. 在这一部分,将根据文献[25]和[34]中的计算,利用{aij}的常秩定理证明定理1. 现在主要任务就是去证明{aij}的常秩定理.假设在点(x0,t0)∈Ω×(0,T)处取得最小秩l.首先假设l≤n-2,否则结果就显然成立了.接着假设u∈C4以及μ0>0.所以存在一个(x0,t0)的邻域O×(t0-δ,t0],使得(aij)有l个被正数控制的“好的”特征值以及其他n-1-l个是(aij)的“坏的”特征值是非常小的.将用G来表示“好的”特征值的指标集并且用B来表示“坏的”特征值的指标集.对任意固定点(x,t)∈O×(t0-δ,t0],可以用(7)形式表示(aij),选择e1,…,en-1,en使得un(x,t)=|∇u(x,t)|>0并且(uij)1≤i,j≤n-1是对角化的. 不失一般性,假设u11≤u22≤…≤un-1,n-1.根据(4)-(5),可以得到(aij)1≤i,j≤n-1是对角化的,并且u11≥u22≥…≥un-1,n-1.为了方便起见,用G={1,…,l}和B={l+1,…,n-1}分别表示“好的”和“坏的”指标集.如果没有混淆的话,还将有下列表示 G={a11,…,all} 和B={al+1,l+1,…,an-1,n-1}. 这里对任何δ>0,可选择O×(t0-δ,t0]是足够小的,对所有(x,t)∈O×(t0-δ,t0]和j∈B有ajj<0. 设 φ(x,t)=σl+1(a), 对于(x,t)∈O×(t0-δ,t0],若存在正数C使得|h(x,t)|≤Cf(x,t),就用h=O(f)来表示. 根据φ的定义,可以得到 aii=O(φ),hii=O(φ),uii=O(φ). 求φ的一阶导,会得到 (17) 因此 类似上述求导,可以得到 (18) 对于任意i∈B,j∈G有 除此之外,还有 接下来,求解出φ的二阶导 (19) (20) 假设u是时空拟凹解并且u的时空水平集是凸的,就会有 因此,可以得到 和 所以,若A足够大有 Fααφαα-φt≤C(φ+|∇φ|). (21) 根据强极大值原理,就可以得到φ=0,即 Rank(aij)≡l(x,t)∈O×(t0-δ,t0]. 由于闭凸超曲面必有严格凸点,那么Rank(aij)≡n-1,Ω×(0,T).通过连续性方法,使得定理1中的严格凸性得证. 在这一部分,将给出定理2的证明.实际上,这个证明类似于文献[25]和[35],但做出了一些修改. 如果没有混淆的话,还将有下列表示 aii=η0eAu+O(φ),hii=η0eAuO(1)+O(φ),uii=η0eAuO(1)+O(φ). 求φ的一阶导,将会得到 (22) 因此 类似上述求导 (23) 接下来求φ的二阶导, (24) 对于任意i∈B,j∈G, 除此之外,还有 (25) 假设u是时空拟凹解并且u的时空水平集是凸的,就会有 因此可以得到 和 若A足够大,就有 (26) κu(x,t)≥η0eAu=min{κ0,κ1e-A}eAu(x,t), (x,t)∈Ω×[0,T). 也就完成了定理2的证明. 利用常秩定理,研究了凸环上一类抛物方程的时空拟凹解的空间水平集的时空拟凹解,给出了空间水平集主曲率的正下界估计.论文完善了一类椭圆偏微分方程解的水平集的曲率估计,对于进一步完善抛物方程的几何意义具有重要的帮助. 致谢感谢审稿人的仔细阅读和修改意见.3 定理1的证明

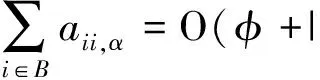

4 定理 2的证明
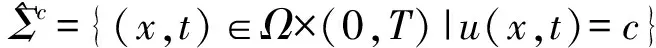

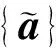
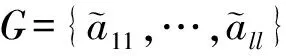
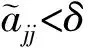
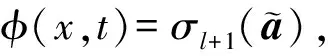





5 结 论

