三相虚拟磁链观测并网逆变器预测技术

荆江平，余小婵，刘 元

(1.国网江苏省电力有限公司电力调度控制中心，江苏 南京 210024；2.上海电力大学电子与信息工程学院，上海 200120；3.长沙理工大学清洁能源与智能电网湖南省协同创新中心，湖南 长沙 410114)

逆变电源作为电子电源的一大主流分支，其控制技术发展已日趋成熟。而并网逆变器作为电力变换的主要接口，广泛应用于电力网的传输运行中。

三相并网逆变器的电压型控制方法主要基于电网电压定向控制(voltage oriented control，VOC)和虚拟磁链定向控制(virtual flux oriented control，VFOC)，目前，主要采用电网电压定向控制策略，通过采样电网电压、电网电流以及直流输入电压进行反馈控制。但是，众多的传感器也带来了高成本、复杂性和可靠性差等问题。文献[1]采用了传统三相LCL逆变器控制策略，基于电压外环与电容电流内环以消除谐振尖峰所引起的系统振荡；文献[2]应用一种单相无电网电压传感器的模型，采用了有功功率和无功功率的电网电压估计方法，其结构过于简单，模型相对比较单一；文献[3]主要针对虚拟磁链的直接功率控制方法，其通常需要过高的采样频率；文献[4-5]采用各种方式减少传感器，但均尚未进行很好的电流保护，工业应用不多。

本文设计一种基于虚拟电网磁链估算策略，设计无电压传感器的并网电压估计算法，通过电路阻抗分析估计所需控制变量，从而消除并网电压传感器。最后，通过无差拍预测电流控制算法预测下一时刻电流，进而控制VSI变换器，其广泛适用于中、大型并网控制系统中。

1 无电压传感器并网模型分析

1.1 三相LCL无电压传感器并网控制模型

通用型三相LCL并网逆变器基本结构如图1所示，Via、Vib、Vic为三相桥臂输出电压，Vga、Vgb、Vgc为三相并网电压；iLa、iLb、iLc为逆变器侧三相电流，iga、igb、igc为三相并网电流，ica、icb、icc为滤波电容电流；VDC为直流电压，CDC为直流母线电容；R1、L1分别为逆变器侧三相寄生电阻与电感，Rg、Lg分别为电网侧三相寄生电阻与电感；Cf为LCL滤波电容[6]。

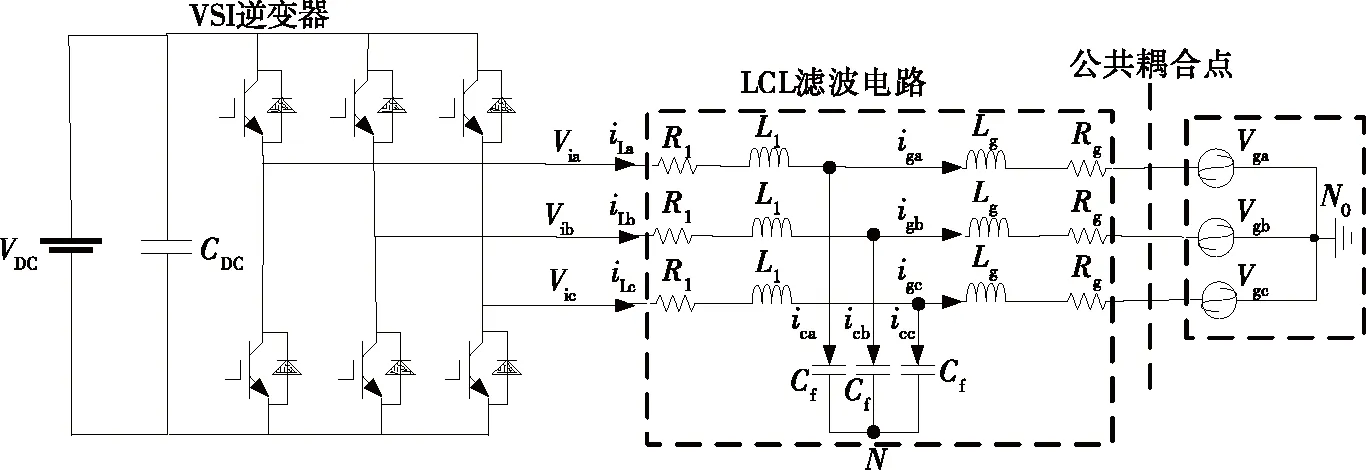
图1 三相LCL 并网逆变器主电路拓扑结构Figure 1 Three-phase LCL grid-connected inverter main circuit topology diagram

将abc三相自然坐标系经由clark变换到αβ两相静止坐标系下，由基尔霍夫电路定律可知,可得αβ两相静止坐标系下LCL并网逆变器的数学模型：

(1)

1.2 无电压传感器磁链估计策略

在两相(αβ)参考系中，采用虚拟磁链估计(virtual-flux oriented estimate，VFOE)策略，其矢量控制通常以基于虚拟磁链为基础，此种控制方法类似于以观测交流电机磁链的相同理论来观测虚拟电网磁链，从而可以间接地观测电网电压。通过对式(1)中的第1式左右两边同时积分，即可得到其虚拟电网磁链观测式：

(2)

由于电网电压空间矢量具有超前于虚拟电网磁链空间矢量π/2角度、幅值增加ω倍的特点，因此，可得坐标变换中所应用到的正余弦计算表达式、电网电压空间矢量角以及幅值：

(3)

(4)

式中ψα、ψβ为αβ坐标系下虚拟电网磁链；θs、θψ分别为电网电压、虚拟电网磁链的空间矢量角；Vm、ψm分别为电网电压、虚拟电网磁链的空间矢量幅值；ω为电网电压空间矢量旋转角频率[7]。

由式(2)、(3)可推算出电网电压的估算表达式：

(5)

由式(5)数学模型推导分析，可将虚拟磁链思想应用到电容电网电压磁链观测器设计中，可得：

(6)

2 无电压传感器观测器设计

2.1 滤波电容电压观测器设计

αβ两相静止坐标系下的电容电压表达式见式(1)中的第3式，其中，Viα、Viβ可根据直流母线电压以及三相逆变器开关函数Sa、Sb、Sc(Si=1使得相应上桥臂导通；Si=0使得相应下桥臂导通)估算出来，其表达式为

(7)

采用空间矢量SVPWM调制方法，由于PWM周期时间短，故开关状态Sa、Sb、Sc可用平均占空比Da、Db、Dc来代替[8]，式(7)可改写为

(8)

由于式(1)中的第3式存在导数项，直接计算困难，故引入虚拟磁链消除微分项[9]，得到αβ坐标系下电容电压磁链计算式为

(9)

依据虚拟电网磁链理论，可推得滤波电容电压表达式：

(10)

2.2 电容电压虚拟磁链估算补偿设计

由式(9)可知，针对积分项的出现，直接使用会带来因初值所导致的直流偏置问题，增大系统控制误差。由此考虑使用一阶低通滤波器代替纯积分环节，但仅采用低通滤波器(low pass filter，LPF)会存在相位误差。故为提高三相并网逆变器性能，对LPF产生的相角和幅值误差进行补偿设计[10]。

LPF与纯积分器的矢量关系如图2所示，ψe=|ψe|∠θ表示两相静止坐标系下的磁链定义式，ψ′e=|ψ′e|∠θ′则为经过LPF之后的磁链空间矢量。由图2可知，两者存在一定的相角偏移，ω=314 rad/s为电网的基波角频率，两者关系为

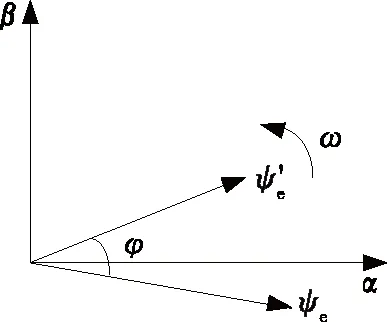
图2 LPF与纯积分器的矢量关系Figure 2 Vector diagram of LPF and pure integra

(11)

在式(11)中，为了减小相角差，须设置较小的截止频率，但ωc过小则会导致LPF很难滤除虚拟磁链估算中的直流分量。因此，截止频率设置的最优范围是0.2～0.3ω，能够保证滤除电压估算过程中的直流分量，但同时会导致仍然存有部分幅值和相位误差，进而提出改进型的相位补偿措施，其补偿设计方案如图3所示。

图3 LPF补偿设计方案Figure 3 LPF compensation design plan

2.3 电网电压观测器设计

电网电压观测器设计主要目的是为了获取空间电网电压旋转矢量角，应用于dq旋转坐标系下park变换，同时为并网连接提供参考基准。由系统模型框架推导可得，电容电流和桥臂侧输出电流可间接计算出电网电流方程：

(12)

由电容电压观测器估算出相应的电容电压，再由式(12)计算igα、igβ。进而利用式(1)中的第1式得到电网电压观测方程式：

(13)

由式(13)得到电网电压空间矢量角以及坐标变换中所应用到的正弦与余弦计算公式：

(14)

其总体电压观测器模型结构如图4所示。

图4 基于虚拟磁链总体电压观测器结构Figure 4 The structure diagram of the overall voltage observer based on the virtual flux linkage

3 改进型无差拍电流预测控制

依据文献[11]中所提理论，针对三相LCL型并网逆变器对相关数学模型进行简化处理。经式(1)消去Vc后采用一阶前后向欧拉法离散化[12]，可得：

(15)

忽略寄生电阻R1、Rg的线路损耗，同时令ip(k)=ip(k)*(p=α、β)[13]，可得：

(16)

由式(16)推算下一时刻电流值，忽略电容影响，令iLα=igα=i，则k+2时刻α轴电流采样值为

iα(k+2)=(Viα(k+1)-Vgα(k+1))·

(17)

根据式(16)、(17)可得α轴的电流偏差值，令k+1时刻α轴电流误差为2个相邻时刻电流误差平均值，则有

(18)

同理分析4个采样时刻的Vgα电网电压，最终可推得Viα(k+1)，比较出PWM占空比信号。

基于锁相环输出相角作为同步旋转坐标系的相角，假设d轴与电网电压矢量同步[14]，此时，有功功率P和无功功率Q为

(19)

由于电网电压定向时Vgd=Vs、Vgq=0[15]，故式(19)可简化为

(20)

4 三相并网逆变器的仿真与实验分析

4.1 仿真分析

为验证所提策略的可行性，在Matlab 2018b/Simulink中，对虚拟电网磁链的无电压传感器预测电流控制进行仿真，其仿真参数如表1所示。

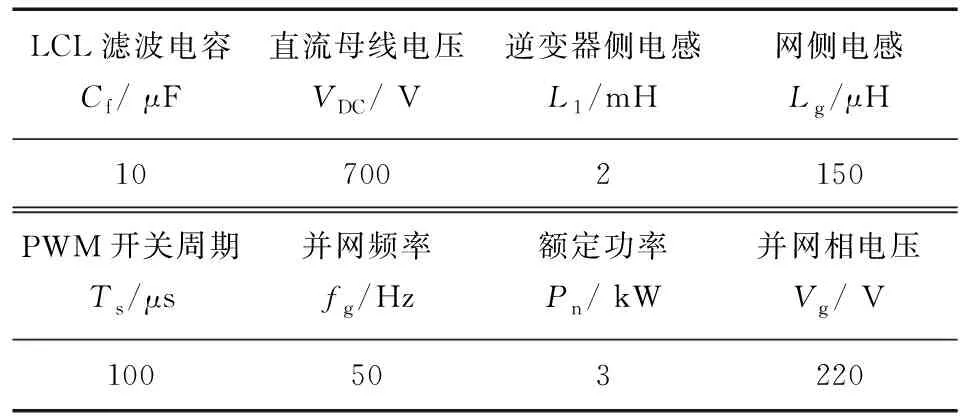
表1 系统主电路参数值Table 1 System main circuit parameters

针对所提的基于虚拟电网磁链的无电压传感器控制策略，进行无电压传感器预测电流控制仿真性能分析，如图5所示，初步检验所提控制策略的有效性，在尽可能减少电压传感器数目的前提下保证控制系统的性能。

图5 无电压传感器预测电流控制仿真性能分析Figure 5 Analysis of simulation performance of voltage sensorless predictive current control

由图5(a)～(d)可知，提出的电网电压观测器策略实现了电网空间角度的估算，且具有良好的线性度；从图5(e)、(f)可以看出，在内环电流控制加延时补偿后，其三相电网电流相较不加延时补偿时正弦度良好，电流的连续性更好；由图5(g)～(i)的a相电网电流的动静态仿真分析可知，控制系统的动静态性能良好。

4.2 实验验证

为验证所提策略的可行性，数字控制器采用 TI公司的浮点型DSP芯片(TMS320F28069)，以采样电路、三相逆变桥控制电路以及其他硬件电路电子器件搭建实验平台。系统总设计参数见表1。

4.2.1 对比实验

1)LPF补偿实验。

基于无差拍预测电流控制与虚拟磁链电压观测器控制相结合，由于LPF在进行虚拟磁链估算时会引起一定范围的相角差，因此，为提高系统性能进行LPF补偿实验，如图6所示，可以看出，图(a)中电流超前电压一定角度，图(b)中电流与电压同相位。由实验结果分析可知，补偿后提高了系统的精度与性能，且经补偿后输出电流谐波畸变率相应减少，曲线更平滑。

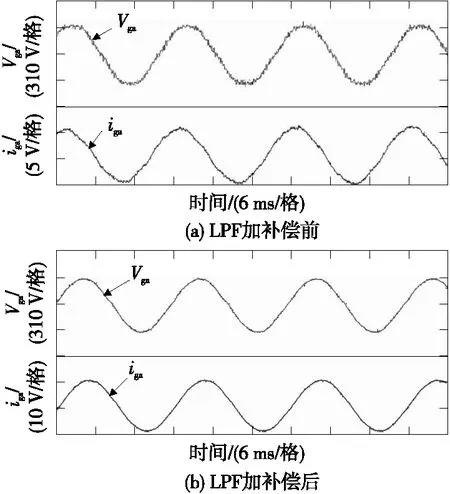
图6 a相电网电压和电流LPF补偿实验Figure 6 LPF compensation experiment of a-phase grid voltage and a-phase grid current

2)无电压传感器电网电压估算策略。

针对所提的无电压传感器电网电压估计策略，有电压传感器状态下a相电网电压与电网空间角度，以及电网电压观测模式下估算的a相电网电压与相应的电网空间角度实验波形如图7所示，通过电压观测器策略实现了电网空间角度的估算，具有很好的线性度。

图7 a相电网电压与电网空间角度对比实验Figure 7 Comparison experiment of a-phase grid voltage and grid space angle

3)传统与加延时补偿的预测电流控制对比。

在结合无差拍预测电流控制策略时，对传统预测电流控制以及加延时补偿的预测电流控制策略分别进行对比实验，如图8所示，可以看出，图(b)相比于图(a)状态下电流正弦度良好，电流畸变率相较变小，输出电网电流的连续性相较更好。

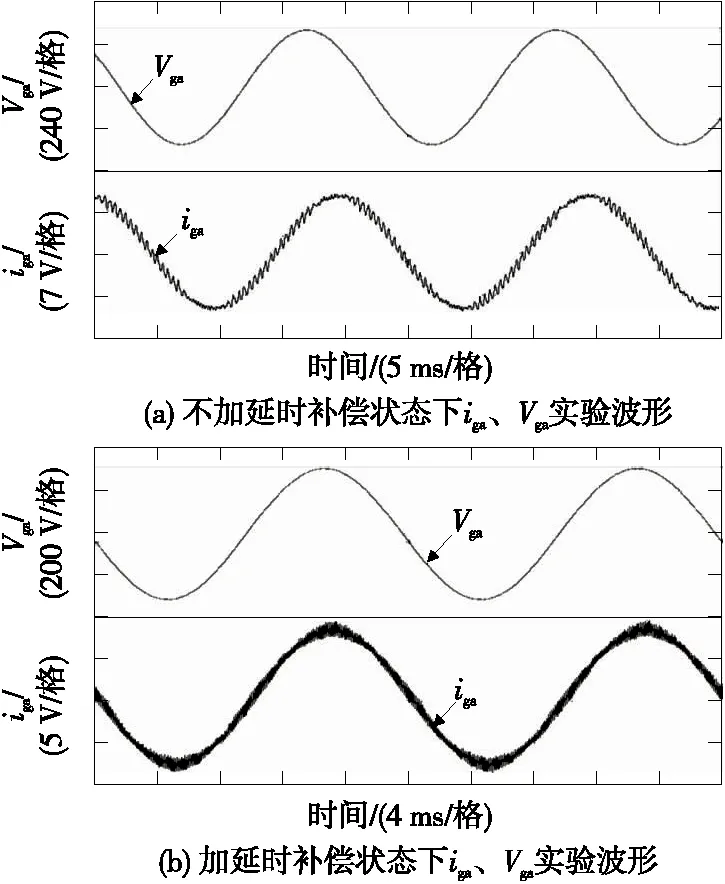
图8 预测电流控制实验波形Figure 8 Waveform of predictive current control experiment

4.2.2 稳态实验

在给定igd=8 A、igq=0 A的状态下，系统输出的稳态实验波形如图9所示，可以看出，图(a)中网侧电流THD保证低于5%，满足并网电流要求；图(b)为αβ坐标系下虚拟磁链观测器估算出的ψα、ψβ实验波形，呈正弦状态，稳定运行后ψβ滞后ψα90°；图(c)为给定igd=7、igq=3 A的状态下加无功补偿后的a相电网电压和电网电流实验波形，电流滞后电压一定角度。

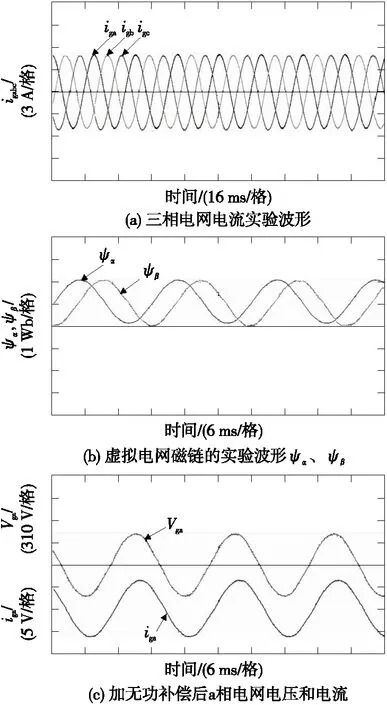
图9 稳态实验波形Figure 9 Steady state experiment waveform

4.2.3 动态实验

1)突增有功电流实验如图10(a)所示，由igd=4 A、igq=0 A突加电流igd=8 A、igq=0 A。

2)突减有功电流实验如图10(b)所示，给定igd=8 A、igq=0 A，稳定运行后突减电流igd=4 A、igq=0 A。

由图10可以看出，动态性能实验验证了所提策略的有效性，实现了dq旋转坐标系下的功率控制，igd控制有功功率，igq控制无功功率，具有良好的动静态性能。

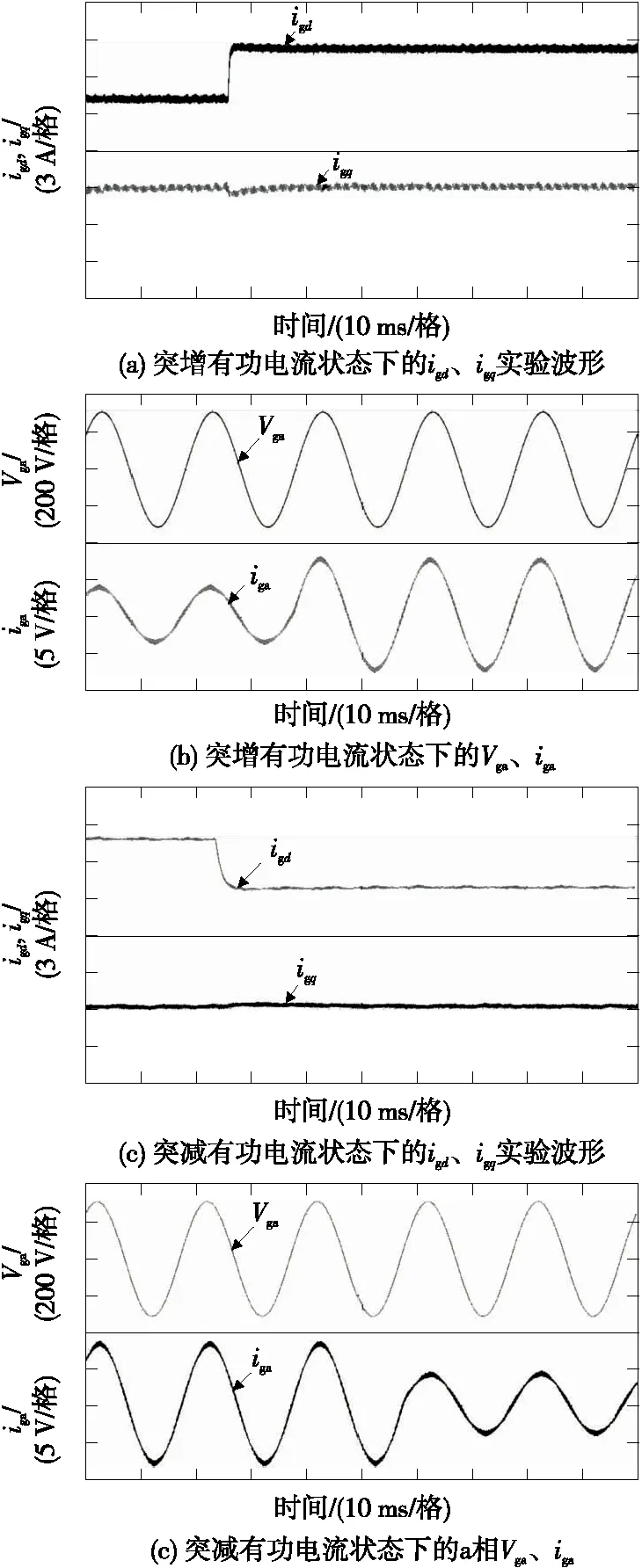
图10 动态实验波形(加延时补偿)Figure 10 Dynamic experimental waveform (plus delay compensation)

5 结语

对三相LCL并网逆变器系统进行研究分析，本文提出基于虚拟电网磁链的无电压传感器控制且与加延时补偿的无差拍预测电流控制算法相结合，应用于并网逆变器系统中。所提出的电网电压观测器控制策略可广泛应用于各种场合，采用较少的电压传感器，节约了成本和系统空间大小，且在电压传感器有磨损以及测量不准确时仍能够继续正常运行，增强了系统的可靠性。结合了改进型加延时补偿的预测电流控制算法，通过对k+2时刻采样电流进行超前预测分析，避免了传统意义上存在的控制延时问题，抗扰动性能更好。