多主体博弈下基于改进NashQ算法的风电场调度策略

郑海林，朱振山，温步瀛，翁智敏

(福州大学电气工程与自动化学院，福建 福州 350108)

随着“碳达峰”与“碳中和”目标的提出，要实现中国能源结构的转变，可再生能源机组的装机必将逐步增长，未来风电也将大量接入电网。但风力发电的波动性、间歇性以及随机性为其大规模并网带来了极大的挑战[1-2]。受政策补贴的影响，电网公司优先保证风电上网[3-4]，但随着2016年来中国陆上风电4类风区上网指导价连续4次下调，风电的政策补贴红利逐步减少，参与竞争性电力市场成为未来风电的发展趋势。因此，考虑多方投资主体博弈下的风电调度策略成为当今重点关注的研究方向之一。

近年来，为了平抑风电出力的波动性与不确定性，中国各省份陆续出台了一系列强制风电企业配置储能的政策，但储能高昂的配置成本、运行成本以及辅助服务市场尚未完全建成一定程度上影响了风电投资主体配置储能的积极性。此外，电动汽车(electric vehicle，EV)因其环保、经济等优势而被广泛应用[5]，极大地推动了电动汽车充电站和充电桩的建设[6]。相比于短时间内为风电场配置大量成本高昂的储能，利用已有的电动汽车充电站资源参与风电场联合调度的思路更具有可行性[7]。

目前关于风电优化调度的研究主要有2类：一类是从风电运行效益的角度设定目标函数，建立优化调度模型，从而优化风电运行，如：可再生能源弃电量最小化[8-9]、风电波动与预测偏差的最小化[10-11]、可再生能源的环境效益[12]以及政策补贴[13]等；另一类将风电视作电网的一部分，从电网运行效益的角度设定运行目标，从而优化风电调度策略，如：电网运行成本最小化[14]与用户的用电成本最小化[15]、电网的环境效益[16]以及电网的电压稳定性[17]等。但由于电网中的发电设施是由不同的投资主体建设的，将电网视为整体进行调度，未能充分考虑各投资主体的效益，不利于调动各方的积极性。从风电角度优化风电调度策略的文献仅考虑了风电场投资方效益的最大化，忽视了其他投资主体的效益，无法反映风电进入电力市场后的真实效益。从长远的角度来看，不利于风电场进入竞争性电力市场后的可持续发展。

考虑到风电机组出力的不确定性以及电网内各方投资主体决策的相互影响，无法通过简单的优化方法来获得最佳的运行策略。现有文献通过Nash均衡博弈与强化学习的结合，采用多智能体强化学习来求解这一复杂问题。文献[18-19]引入多智能体强化学习方法来求解多智能体博弈问题，从而优化电网内多方主体的调度策略；文献[20]在这一基础上，通过强化学习Q矩阵的迁移从而提高算法的在线学习速度；文献[21]引入资格迹更新技术提高多智能体博弈和迁移学习的收敛速度。以上文献所采用的多智能体强化学习算法中，智能体的学习往往局限在自身的学习经验，对外界环境不敏感，使得收敛速度较慢，会产生较大的计算成本。

因此，针对现有研究的不足，本文提出一种多主体博弈环境下基于改进NashQ算法的风电调度策略，综合考虑风电场、火电厂、储能电站以及电动汽车充电站各方的效益，兼顾风电场的预测偏差考核、绿证收益与售电效益，构建多方博弈下风电场调度、风—储联合调度与风—车联合调度的优化模型。采用多智能体强化学习算法进行求解，并引入JS(Jensen-Shannon)散度对比Nash均衡分布与历史经验分布来优化NashQ算法中各智能体学习率，提升算法的求解效率，用以求解多主体序贯决策问题。此外，通过对算法中Q矩阵的训练，提升算法在线求解的速度，使得算法可以灵活适应不同博弈环境。算例仿真结果验证本文算法的求解性能以及风电场与电动汽车充电站联合调度策略的优越性。

1 多主体博弈建模

1.1 电网系统结构

电网系统结构主要由火电厂、风电场、储能电站以及电动汽车充电站和其他用电负荷等组成，本文所讨论的电网系统为输电网层级，其结构如图1所示。

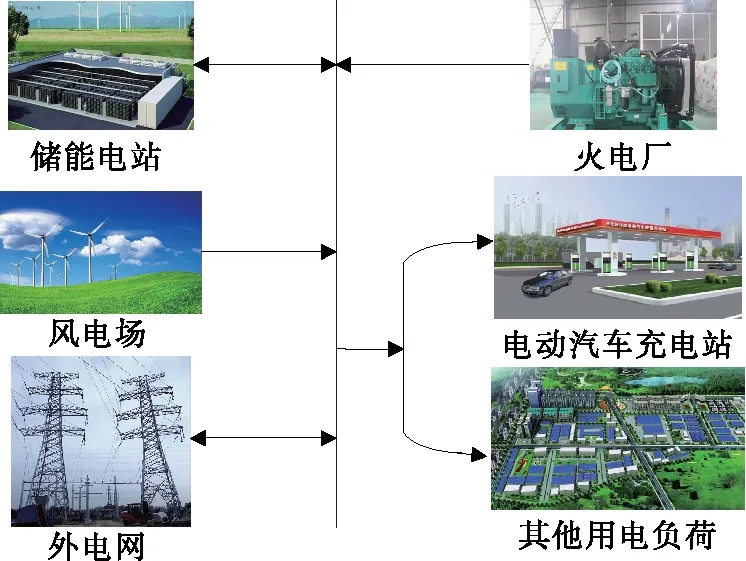
图1 输电网系统结构Figure 1 Schematic diagram of transmission network

1.2 博弈主体基本模型

1)风电场主体。

为了保证电网内功率动态实时平衡，要求可再生能源电站的实际出力与预测出力曲线应基本一致，偏差的发电量或电量不足需要缴纳较高的罚金。风电场主体独立运行时目标函数为

(1)

Sw,t=(pw+pgr)·(Pw,t-Paba,t)·Δt

(2)

Cw,t=((Pw,t-Paba,t)·pwo+|Pw,t-

Paba,t-Ppre,t|pwη)·Δt

(3)

式(1)～(3)中Sw,t为风电场的售电效益；；Cw,t为风电场的成本；Cws为风电场分摊的为风电场分摊的辅助服务费用；Pw,t为风电场t时刻气象条件下最大出力；Paba,t为t时刻风电场弃风功率；(Pw,t-Paba,t)·pwo为风电场的运行成本；|Pw,t-Paba,t-Ppre,t|pwη为风电场实际出力与计划出力偏差的惩罚，风电场的实际出力等于在该时刻风速下的风电场最大出力减去风电场弃风功率；pwo为风电运维成本；Ppre,t为t时刻的预测风电出力；pw为风电上网的价格；pgr为风电的绿证价格；η为偏差考核比例；风电的弃风比例应不超过μ，限制条件为Paba,t≤Pw,t·μ。

2)电动汽车充电站主体。

当电网内发电机组出力不足以满足负荷需求时，充电站通过补助EV用户，削减充电需求，满足电网供需平衡。充电站的目标函数为

(pe1-Δpt)-pevo)·Δt

(4)

pevo=plc+psc

(5)

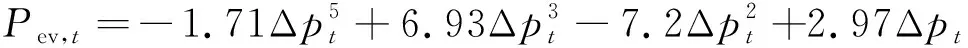
3)火电厂主体。

火电厂的收益一部分为直接售电的效益，另一部分则是火电机组响应电网内功率需求调整自身出力提供AGC服务的收益，目标函数为

(6)

式中SMT,t为火电机组的运行收益；CMT,t为火电机组的运行成本；CMTs为火电机组分摊的辅助服务费用。

成本函数为

(7)

式中 第1项为机组的发电成本；第2项为机组的爬坡成本[21]；第3项为机组的启停成；a、b、c为微型火电系统发电成本系数；PMTi,t为微型火电系统第i台机组t时刻发电量；i=1,2,…,N为微型火电机组数；ΔPMTui,t、ΔPMTdi,t为微型火电机组上、下爬坡成本；pup、pdown为微型火电机组上、下爬坡量；hi,t为第i台机组t时刻的启停状态，1为启机，0为停机；pon、poff为启停机成本。

火电厂的收益为

pAGC·ΔPAGC,t

(8)

式中 第1项为火电机组的售电效益；第2项为火电机组响应AGC服务补偿；pMT为火电机组上网电价；pAGC为AGC辅助服务单位电量补贴，当火电的出力调整与电网中功率偏差相反时，ΔPAGC,t取为正，即火电机组获取AGC响应补偿；反之则取为负，作为调节偏差的惩罚。

火电机组运行需要满足机组的爬坡约束以及机组最大、最小功率的约束，即

(9)

式中PMTi,min、PMTi,max分别为微型火电机组功率最小、最大值；ΔPMTi,max为机组爬坡功率上限。

4)储能电站主体。

储能电站的目标函数为

(10)

储能电站的收益为

(11)

储能电站的成本为

(12)

式中 第1项储能充放电损耗成本；第2项为储能全寿命周期成本；ηcha、ηdis为电池储能的充放电效率；d为贴现率；n为电池使用年限；Ces为电池本体成本；Lmax为电池年平均最大使用次数。

电池储能系统运行需要满足充放电最大功率、荷电状态约束，约束条件为

(13)

5)辅助服务费用分摊模型。

电网内的辅助服务费用由发电企业按发电量进行分摊[23]，即

Δt+Sev+pet|Pet,t|)

(14)

式中 第1项为火电机组AGC服务补偿，第2项为储能调频服务补偿，第3项为EV用户调节需求响应补偿，第4项为联络线功率传输费用；Pet,t为t时刻电网内功率不平衡引起的联络线上功率响应，本文设定联络线的传输容量约束为2 MW；pet为t单位功率传输成本。

常规火电系统承担费用CMTs与风电场承担费用Cws为

(15)

式中W为发电企业的总发电量。

1.3 多主体联合博弈

1)多主体博弈模式。各主体基于某一时刻下各方的状态，决策下一时刻动作，且各主体的策略受到其他主体影响，为混合策略博弈。

模式1 风电场与电动汽车充电站联合参与多主体博弈，参与博弈的主体有火电站、储能电站以及风—车联合运行主体。风—车联合运行的优势在于当风电出力小于预测出力时，可以通过减少EV充电需求来减少风电的预测偏差惩罚。

模式2 风电场配置对应的储能联合参与多主体博弈，参与博弈的主体有火电站、储能电站以及风—储联合运行主体。当风电出力小于预测出力时，电池储能对外放电；反之则对储能电池充电。

2)风—车联合运行模型。风—车联合运行效益为

(16)

式中 第1项为EV减少充电需求后风电场等效出力下的运行效益，第2项为电动汽车充电站减少风电场预测偏差后的调节补偿；Pw′,t为风—车联合运行下风电场实际出力，Pw′,t=Pw,t+Pev1,t，其中Pev1,t为EV减少充电需求用于减少风电出力偏差部分；Pev′为风—车联合运行下充电站的实际调节电量，Pev′,t=PEV·N·Pev,t-Pev1,t。参与博弈的主体效用函数包括式(6)、(10)、(16)。

3)风—储联合运行模型。风—储联合运行效益为

(17)

式中 第1项为储能参与减少风电预测偏差后风电场等效出力下的运行效益，第2项为电池储能减少风电场预测偏差后的峰谷套利与调频补偿带来的收益，第3项为电池储能充放电产生的成本；Pw″,t为风—储联合运行下风电场实际出力，Pw″,t=Pw,t+Pcha1,tηcha+Pdis1,t/ηdis，其中Pcha1,t、Pdis1,t为电池储能用于满足风电出力偏差部分；Pes′,t={Pcha′,t;Pdis′,t}={Pcha,t-Pcha1,t;Pdis,t-Pdis1,t}，{Pcha′,t;Pdis′,t}为风—储联合运行下储能电池的实际充放电电量。参与博弈的主体效用函数包括式(6)、(10)、(17)。

2 改进NashQ算法

2.1 强化学习

强化学习是学习状态与行为之间的映射关系，通过感知环境状态以及奖励学习和决策的过程。Q学习是一种普遍应用的强化学习算法，其递归方程为

Q(s,a)t+1=(1-α)Q(s,a)t+

(18)

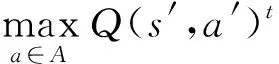
2.2 NashQ算法

当博弈中其他智能体的策略均给定时，智能体不再改变自身策略，即为Nash均衡，有

(19)

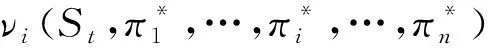
引入多智能体博弈环境，Q值的值函数及迭代公式为

Qi(s,a1,a2…,aN)t+1=(1-α)·

Qi(s,a1,a2…,an)t+α·

(20)

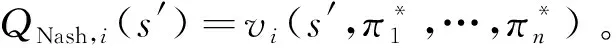
2.3 改进NashQ算法

学习率会影响智能体的学习速度，当学习率取值较大时，智能体对于新尝试结果的占比越高，对于历史经验遗忘率也就越高；当学习率取值较小时，智能体接受新尝试结果比例较小，使得学习效率下降。而大多数研究强化学习的文献往往将学习率取为定值，把较优的学习经验与较差的学习经验混合，大大降低了学习速度，影响智能体的收敛速度。

KL散度(kullback-leibler divergence)又称为相对熵，是2个概率分布P和Q差别的非对称性的度量，用于衡量2种分布的相似度。由于KL散度是不对称的且不满足三角不等式，故

DKL(P,Q)≠DKL(Q,P)

(21)

DKL(P,Q)>DKL(Q,S)+DKL(S,Q)

(22)

JS散度是KL散度基础上的变体，可以有效地解决KL散度存在的问题。当2个概率分布较远时，KL散度没有意义，而JS散度仍可以衡量2个概率分布的相似度。

引入JS散度优化各智能的学习率后的NashQ算法流程如图2所示。引入JS散度优化各智能体的学习率αi,t，即

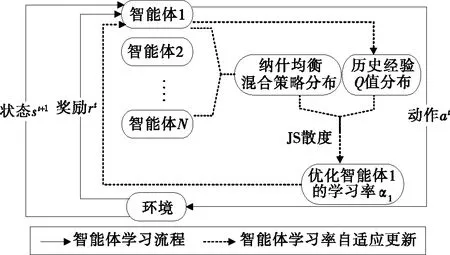
图2 改进NashQ算法流程Figure 2 The process of improved NashQ algorithm

(23)

(24)

(25)

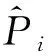
3 基于改进NashQ算法的风电调度策略

3.1 状态空间

3.2 动作空间

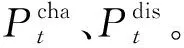
3.3 算法流程

改进NashQ算法中采用ε-greedy贪婪算法对动作空间进行探索，动作的探索为

(26)

式中ε0∈[0,1]为贪婪搜索算法的探索率，取较小正数；ai,rand为智能体i随机选择的动作。

判断多智能体强化学习过程中各个智能体的收益是否趋于收敛，收敛判据为

(27)

其中，σ为较小正数，本文取为0.015；Qi,t为第i个智能体第t次循环得到的Q值表。若各个智能体Q矩阵均收敛则结束学习，输出最优策略；反之则继续循环。

基于改进NashQ的风电调度策略的流程如图3所示。

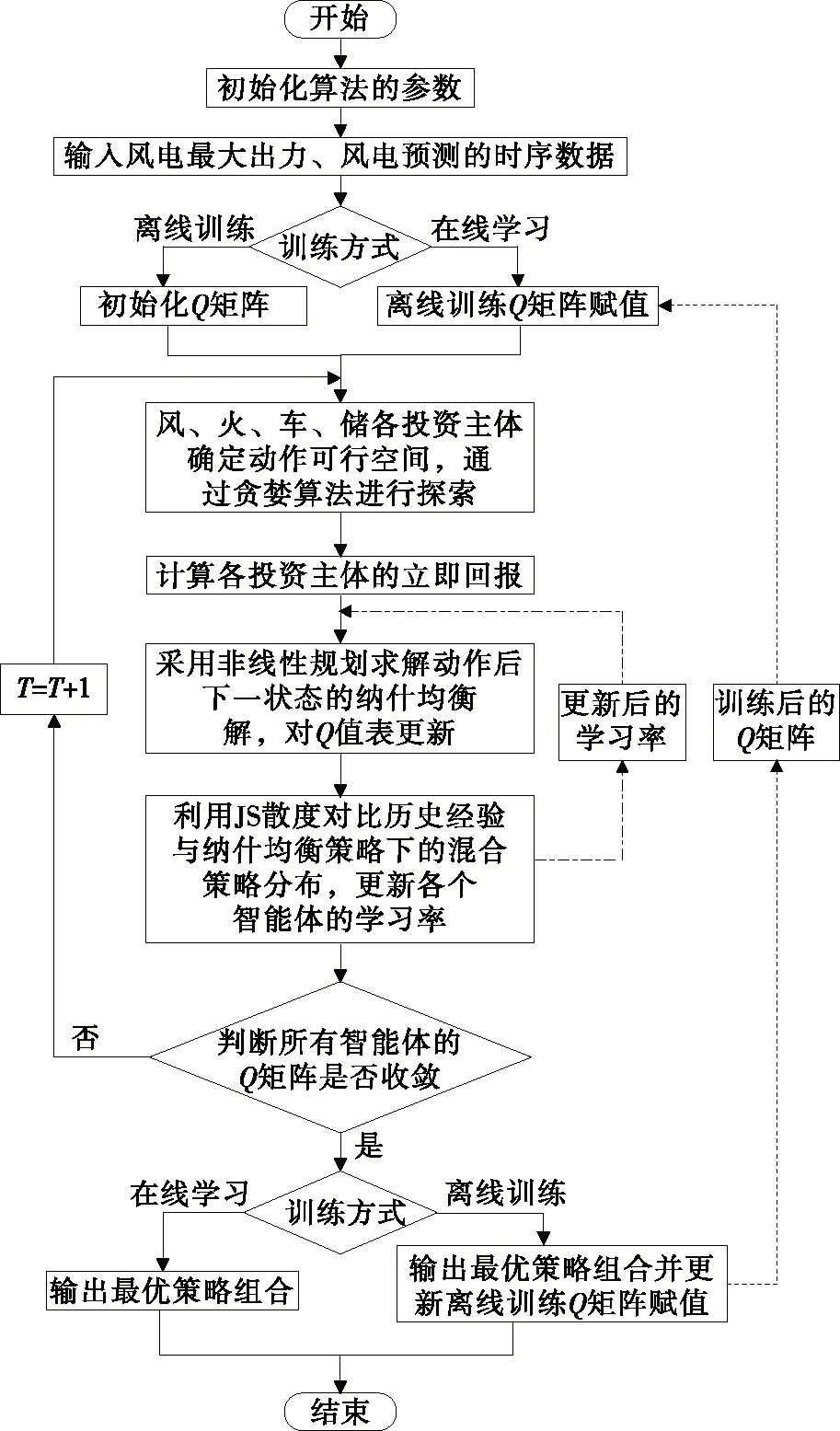
图3 风电调度策略的流程Figure 3 The process of wind power dispatching strategy

4 算例分析

4.1 算例概况

本文以某个风电场所在地区的电网为例，由250 MW风电场、8 MW·h储能电站、2台火电机组的火电厂以及1个电动汽车充电站组成，辅助服务补偿价格、电网分时电价以及各设备参数分别如表1～3所示；算法参数设置如表4所示；算法典型日风电、预测以及用户负荷曲线如图4所示。

表1 辅助服务补偿价格Table 1 Auxiliary service compensation price

表2 电网分时电价Table 2 Time-of-use tariff 元/(kW·h)

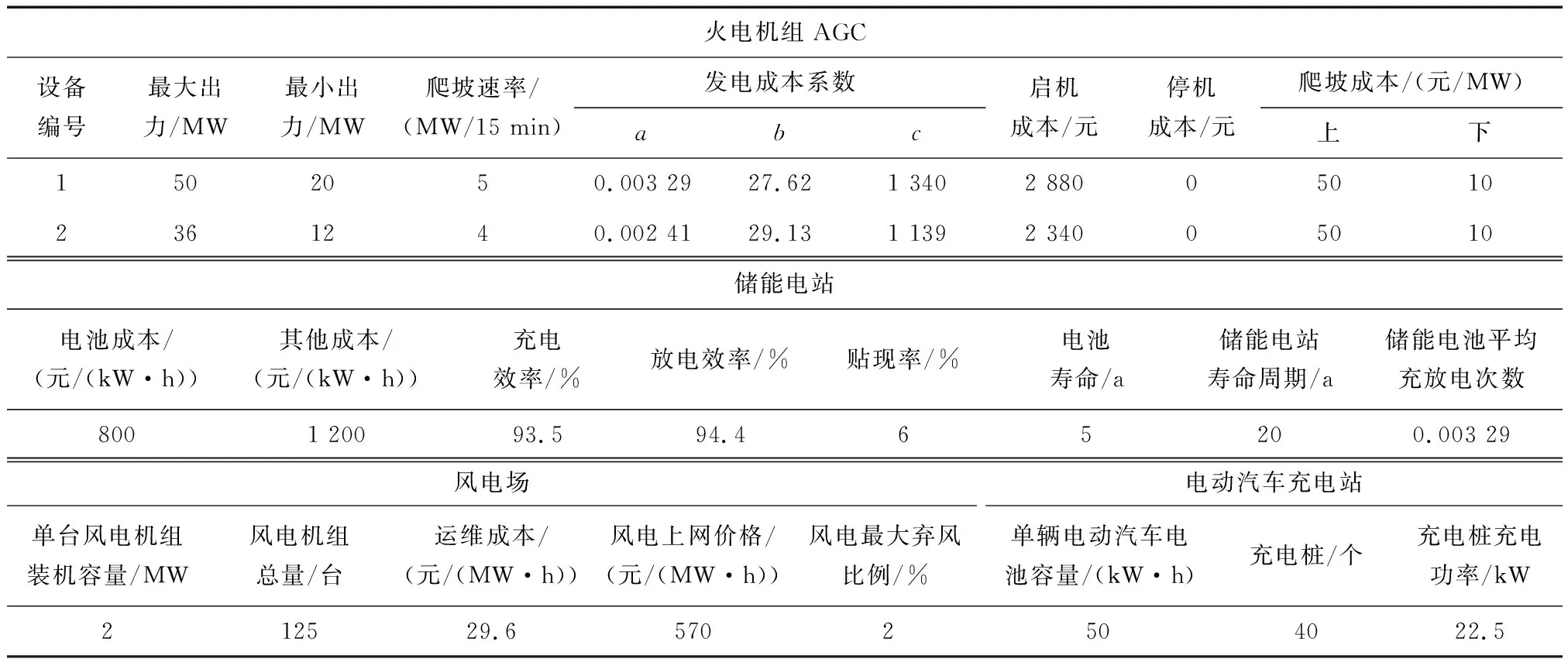
表3 设备参数Table 3 Equipment parameters

表4 算法参数Table 4 Algorithm parameters

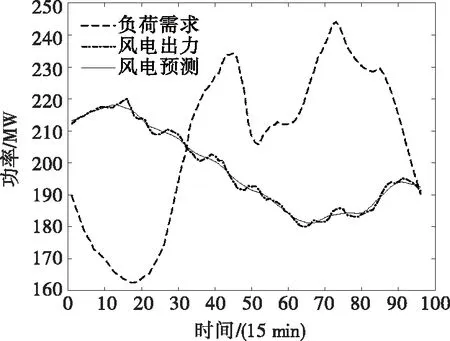
图4 典型日风电、预测以及负荷曲线Figure 4 Typical daily curve of wind power，forecast and load

将可再生能源功能状态按照可再生能源出力/电网内负荷需求之比、风电最大出力上限以及预测出力偏差量对其定义，划分为1天96个状态，火电机组包含启机与停机2种状态、储能包含充电/闲置/放电3种状态。火电厂、风电场、储能电站以及充电站的动作离散为9、6、6、11个离散空间。

4.2 Nash均衡证明及改进Nash结果分析

NashQ算法收敛的具体证明过程可参考文献[24]。为了保证NashQ算法能够找到Nash均衡解，则对于任一时间与状态下，各个智能体均能寻找到一个全局最优点或者鞍点，可用于更新Q矩阵。由于在电网中风电出力具有不确定性，无法保证每个时刻均可以找到全局最优点，在部分时刻仅存在鞍点，但鞍点的数目往往不止一个。

1)传统的NashQ算法在存在鞍点的算例中容易出现运算结果在几个鞍点中徘徊选择，容易导致最终结果出现数个结果的情况。

2)文献[21]中引入资格迹，提出NETRL算法，通过智能体自身对于某一状态、动作的访问次数来优化Q值表的更新，虽然提高了智能体自身经验的感知，但忽视了智能体对于外部环境的感知，学习的效果有所提升但提升的有限。

3)本文提出的改进NashQ算法则可以较好地避免这一结果，在NETRL算法的基础上，通过JS散度对比智能体的自身经验与外部环境，提升智能体对外部环境的感知。

本文采用 Matlab2020a 软件进行编程求解，在 Intel i5-6300HQ(主频为2.30 GHz)、内存16 GB 的计算机上运行。利用风电发电系统智能体的收敛判据对比3种算法的收敛结果，收敛所需时间如表5所示，可以看出，本文所提出的改进NashQ算法求解所需时间为NashQ算法的37.3%，也是文献[21]中NETRL算法的46.9%，从而验证了本文所提出的改进NashQ算法的快速收敛性。收敛曲线如图5所示。

表5 3个算法收敛所需时间Table 5 Converge time of the three algorithms

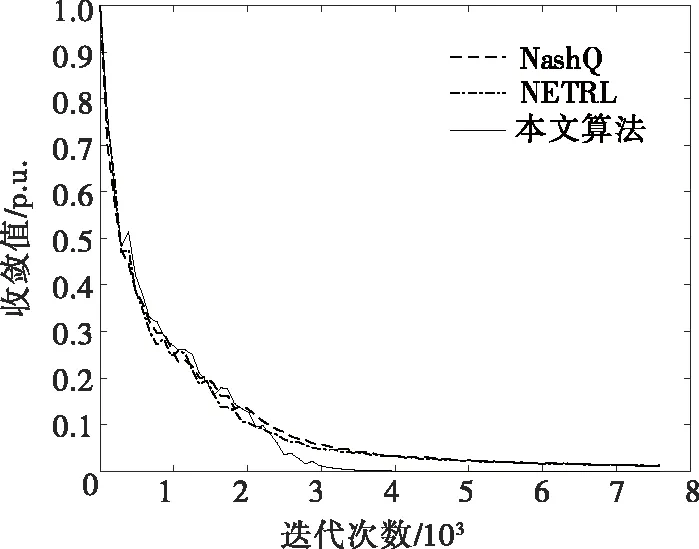
图5 不同算法的收敛曲线Figure 5 Convergence curves of different algorithms

4.3 仿真结果讨论分析

为对比风电不同运行方式下的经济效益，设定3种风电运行场景，并针对高比例可再生能源电网系统运行模式给出优化风电的调度策略：①电网中风电场、电动汽车充电站、火电厂以及储能电站系统共同博弈；②风力发电系统与电动汽车充电站系统联合参与电网中的博弈；③电动汽车充电站转化为同等容量储能电池，风储联合参与电网中博弈。

3种场景下风电场的弃风电量与减少的偏差考核如表6所示，风—车联合运行、风—储联合运行均能减少风电场的偏差考核，其中风—储联合运行下有着显著的优势。对比风电独立运行下弃风电量，风—车联合运行下减少了43.4%，风—储联合运行减少了44.7%。可以看出，风—储联合运行可以提高风力资源的利用率。

表6 3种场景下优化运行结果Table 6 Optimization results under three scenarios

各个投资主体的经济性如表7所示，对比可以看出，风—车联合运行的经济效益优于风电场独立参与电网系统中多主体博弈的经济效益，提高收益20 775.1元。由于充电站系统的补贴成本比风力发电系统的偏差考核惩罚成本低，同时还能为其带来额外的售电效益。因此，风力发电系统与电动汽车充电站系统的联合运行具有实际意义。

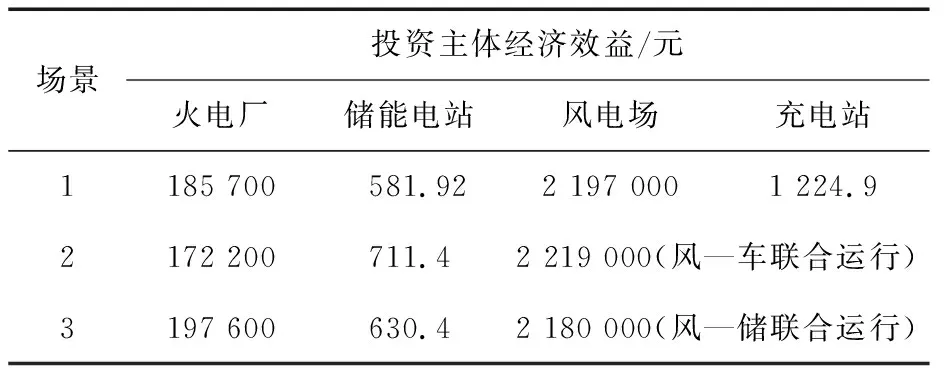
表7 3种场景下各投资主体经济性Table 7 Economics of investment subject under three scenarios

3种场景下风电场调度策略分别如图6～8所示。风—储联合运行由于储能电池系统较高昂的配置成本与运行成本，其经济效益甚至低于场景1中风电场独立运行的经济效益，在不考虑电厂侧储能参与辅助服务市场时，该风电场配置储能的运行模式难以吸引风力发电投资者为风电场配置储能。

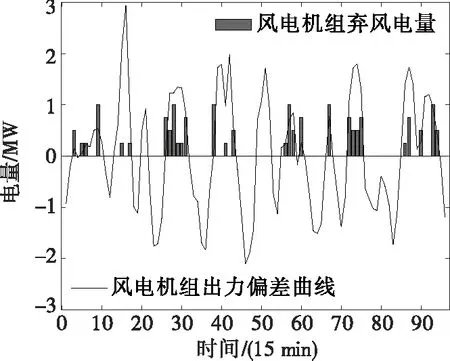
图6 风电运行调度策略(场景1)Figure 6 The operation scheduling strategy of wind power(Scenario 1)

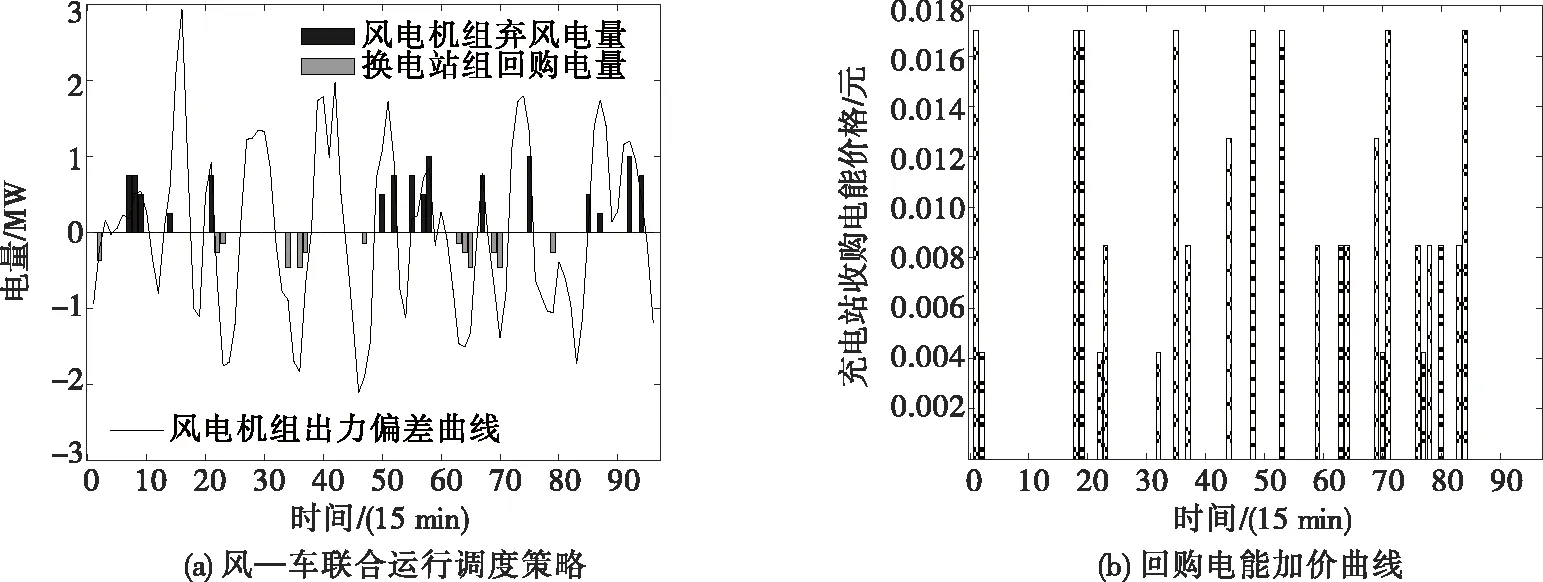
图7 风—车联合运行调度策略及回购电能加价曲线(场景2)Figure 7 The operation scheduling strategy for the wind-mill(Scenario 2)

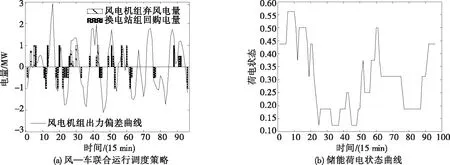
图8 风—储联合运行调度策略及储能荷电状态曲线(场景3)Figure 8 The operation scheduling strategy for the wind-storage(Scenario 3)

4.4 在线仿真结果分析

本文基于2020年每个月抽取3 d的数据作为离线训练数据，训练集内选取6组数据(X1～X6)，训练集外选取6组数据(C1～C6)，检测本文算法的在线决策能力。在线学习与离线训练的对比如图9所示，可以看出，训练、非训练集数据在线学习所需平均时间分别为319.21、427.07 s，相较于离线训练的所需平均时间(507.25 s)分别减少了37.07%、15.81%。因此，通过Q值表的离线训练可以显著提升在线学习的求解效率。

图9 离线训练与在线学习的平均收敛时间对比Figure 9 Comparison of average convergence time between off-line training and online learning

5 结语

本文以风电场作为研究对象，提出一种多主体博弈下基于改进NashQ算法的风电调度策略，分析对比了不同场景下的风力发电系统的效益。

1)综合考虑电网系统内不同投资主体的利益诉求，兼顾风电场的偏差考核、绿证效益以及售电效益，充分挖掘风电场、火电厂、储能电站与电动汽车充电站的调节能力，最大化风电场经济效益；2)提出的改进NashQ算法与NashQ、NETRL算法对比，收敛所需时间分别缩短了62.7%、53.1%，验证了改进NashQ算法的有效性；同时，采用离线训练方式训练Q值表可以显著提高在线学习的收敛效率，缩短收敛所需时间；3)仿真结果表明，风—储、风—车的联合运行相较于风电池独立运行可以分别减少44.7%、43.4%的弃风电量，但由于储能的高昂配置、运行成本，风—储联合运行经济效益较差；而风—车联合运行在减少弃风电量的同时，还提升了二者的经济效益，对于风电投资方与充电站投资方具有一定的吸引力。

后续研究会进一步考虑辅助服务市场中有偿提供辅助服务对于风电调度经济型的影响，为参与竞争电力市场的风电运营模式提供参考。