基于配网规划等值曲线的输配电网协调规划
王明渊,何 凯,王 木
(1.国家电网有限公司,北京 100031;2.电力系统及发电设备控制和仿真国家重点实验室(清华大学电机系),北京 100084)
中国经济社会的快速发展、工业化和城镇化进行加速、煤改电等项目的实施、以及电动汽车充电需求的增加,使得电力负荷需求、特别是城镇和工业园区电力负荷持续增长,这对输电网和配电网传输能力提出了新的要求。基于美国和欧洲电网的实证研究指出,电网容量不足引起的停电损失超过冗余线路的投资成本[1]。为此,需要适度超前开展输配电网规划和建设,以提升电网输电能力、保障电力安全供应、适应中国经济社会发展的需求。
输电网和配电网运行特点不同,规划的模型和方法也有差异,目前已有众多文献分别对输电网和配电网的规划方法进行了研究。在输电网规划领域,文献[2]首次使用线性规划对输电网扩展进行评估;文献[3]提出了以最小化投资费用和可靠性指标的输电网规划模型,从规划阶段降低系统大停电的风险水平;文献[4]提出了考虑新能源不确定性和随机性的电网规划方法;文献[5]提出了一种将可靠性指标转化为经济性指标的电网规划新方法;文献[6]提出了市场环境下的发输电一体扩展规划模型;文献[7]提出了一个以概率模型解决多目标电源电网协调规划模型的不确定性的方法;文献[8]给出了基于可靠性的电源电网扩展规划模型和方法;文献[9]提出了一种适应节能服务环境的电网综合资源规划新方法。在配电网规划方面,早期的配电网规划模型包括变电站规划模型、网架规划模型、变电站—网架联合规划模型以及多阶段规划模型[10]。文献[11]基于变电站规划模型,在电源点、负荷点的基础上考虑了既接受电能又输出电能的传输节点;文献[12]将整个规划范围用地理信息系统网络的坐标系统标识,并以此为基础使用动态规划方法规划馈线路径;文献[13]分析了分布式电源在配电网中的布点规划和考虑分布式电源的配电网扩展规划问题;文献[14]提出一种配电网扩展规划中进行分布式电源选址和定容的方法;文献[15-16]提出考虑电动汽车充电网络的配电网规划模型。
相比于独立规划,输电网与配电网协同规划更具优越性。在物理层面,配电网中新增负荷项目和扩容项目会增加输电网的净负荷,输电网规划中对配网内部新增负荷特性和配网运行特性考虑不足,得到的规划方案可能导致输电网与配电网发展不均衡,进而引起局部阻塞或输电网投资过剩。在经济层面,配电网新增项目会影响输电网净负荷与输电线路规划,新增输电网线路可能影响配电网并网节点的电价进而影响配电网扩建的净收益,电网规划中缺乏对输配电网交互影响的考虑将无法实现全社会福利的最大化。在输配电网协同规划方面,文献[17]针对多电压等级、不同网络结构的输配电系统的综合规划问题进行了研究,提出了开环与非开环混合的输配电系统综合规划问题的近似解决方法;文献[18]对110 kV变电站选址定容及供电范围进行了划分,通过提高片区内所有同级变电站的运行合理性,达到优化输电网与配电网间衔接的目的;文献[19]提出了构建输配电网协调规划模型的技术路线,并提出采用现代启发式优化算法和原始对偶内点法相结合的方法求解规划模型。现有输配电网协调规划的研究通常将配电网规划模型整体纳入输电网规划模型统一建模,或者采用输配电网通过公共连接点迭代协同的方法[20-21]。然而,传统的集中式求解方法在求解较大规模的输配电网协调规划问题时,模型复杂度高、求解效率低,在实际工程应用中面临挑战。
为此,本文提出一种输配电网分层规划的新模式,建立基于配网规划等值曲线的输配电网双层规划模型。其中,配电网以扩建净成本最小为目标,采用DistFlow潮流方程建立规划模型。然后在配电网不同项目总数下,分别优化计算得到对应的配网净收益和配网新增负荷,作为输电网规划模型的输入参数。输电网以考虑各配网规划等值曲线的扩建成本最小为目标,采用直流潮流方程建立规划模型。通过输电网模型的优化计算确定输电网线路的规划方案以及各配网内的项目决策方案。算例分析验证本文所提方法的有效性。
1 输配电网协调规划模式
当前,电网公司在开展配电网规划时需要考虑配电网终端用户未来的发展情况,而在各年度投资预算有限的背景下,电网企业不可能同时满足所有配网扩建诉求,只能优先满足净收益大的配网规划项目。因此,需要协调考虑配网发展决策的经济效益以及输、配电网的扩建成本,以最大化电网扩建净收益为目标,优化决策未来的输电网和配电网规划方案。本文对上述需求建立输、配电网联合规划模型。
1)目标函数:最大化电网扩建净收益。其中,电网扩建净收益=配网新增项目经济效益-(输电网扩建成本+配网扩建成本)。
2)约束条件:输配电网扩建总投资预算以及输电网、各个配网的运行约束。
3)决策变量:表征输电网、各个配网的待选线路投建与否的0/1变量以及各个配网待新增负荷项目(如工业园区、煤改电项目)投建与否的0/1变量。
然而,上述联合优化模型是一个复杂的混合整数二次规划模型,决策变量多,存在“组合爆炸”的问题,难以直接一体化求解。为了实现输配电网联合规划问题的高效求解,本文提出基于配电网规划等值曲线的双层优化求解框架,如图1所示,包括上层输电网和下层配电网规划模型,二者之间通过配电网规划等值曲线相关联。

图1 输配电网协调规划框架Figure 1 Bi-level calculation framework for coordinated transmission and distribution network planning
下层模型中各配电网分别优化计算不同投建项目数量下的配电网最大净收益,生成配网规划等值曲线;上层模型考虑配网规划等值曲线优化决策输电线路投建和各配电网新建项目数量,得到输配网协调规划方案。配网规划等值曲线反映了配网内不同新增项目数量下的最优扩建方案和扩建收益,配网新增项目决策会影响输电网规划,而输电网规划时从整体优化的角度对配网规划的初步结果进行优化筛选,由此兼顾了配网规划的局部最优以及输电网规划的全局最优。
基于输配电网分层建模的思路,在配电网与输电网连接的公共节点处将输电网和配电网进行等效分离:对输电网而言,配电网在公共节点处等效为净负荷;对配电网而言,输电网在公共节点处等效为虚拟的发电机。相较于集中式方法,所提出的双层求解框架将含有多配网的输配电网联合规划问题分散至输电网和各配电网单独求解,过程中无需输电网与配电网双方互相知晓对方网络的网架结构参数,将联合规划问题的计算难度由指数复杂度降低为代数复杂度,可实现模型的高效求解。
2 基于配网规划等值曲线的输配电网协调规划模型
在提出的输配电网协调规划模式基础上,结合电网规划的实际需求建立基于配网规划等值曲线的输配电网协调规划数学模型。
2.1 配电网规划模型

2.1.1 目标函数
配电网规划目标函数为
(1)
(2)
(3)
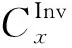
2.1.2 约束条件
1)线路潮流和电流上下限约束。
对于已有线路:
(4)
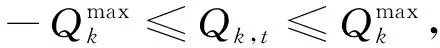
(5)
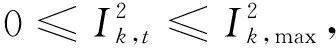
(6)
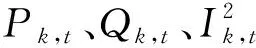
对于新建或改造线路:
(7)

(8)

(9)
2)Dist-Flow潮流约束。
①等式约束。
针对已有线路:
(10)
针对新建或改造线路:
∀t,k∈ΚP
(11)
∀t,k∈ΚP
(12)
②SOC不等式约束。
∀t,k∈ΚE∪ΚP
(13)
3)节点功率平衡约束。
①对于与主网连接的公共节点x。
(14)
(15)
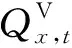
②对于配网其他节点。
(16)
(17)
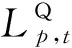
4)公共节点虚拟电源出力控制。
(18)
(19)
5)节点电压幅值。
(20)
(21)
6)配电网项目总数控制。
(22)
式中m为配网新增的项目个数。
2.2 配网规划等值曲线
为解决配电网—输电网协同规划时出现的组合爆炸问题,提出配网规划等值曲线的概念和方法,具体方法说明如下。
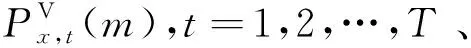
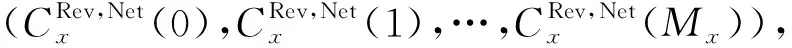
本文将配网项目数与相应配网净收益(配网售电收益减去配网新建线路投资)的关系曲线称为配网规划等值曲线,这是因为在设计的输配协调规划模式下,本文将其作为后续输电网规划模型的输入参数。从输电网的角度来看,输电网规划更关心配网整体的新增负荷、投资和收益情况,并不关注配网中具体项目的组合情况,因此,本文采用配网规划等值方法能够减少输电网规划模型决策变量的规模,从而提升模型的求解效率。
2.3 输电网规划模型
2.3.1 目标函数
输电网规划的目标函数为综合考虑配网投资净收益和输电网投资成本的净成本最小(输配电网扩展总成本最小),即
(23)
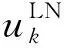
2.3.2 约束条件
1)功率平衡约束。
(24)

2)线路潮流约束。
①对于已有线路,潮流方程为
∀t,k∈ΩELN
(25)
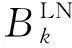
线路传输容量约束:
∀t,k∈ΩELN
(26)
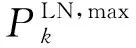
②对于备选线路,潮流约束为
(27)
(28)

线路传输容量约束:
∀t,k∈ΩPLN
(29)
式中ΩPLN为备选线路的集合。
3)节点电压相角及发电机出力约束。
(30)
(31)
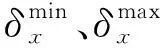
4)配网投资方案总数约束。
(32)
式(32)表示输电网规划最多选择一种配网项目的组合方案。
5)配网投资总额约束。
(33)
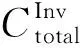
经输电网规划模型的优化后即可确定最终的配网项目决策方案以及输电网线路的规划方案。
3 输配电网协调规划双层模型的求解
本文所建双层规划模型中配电网是MIQCP模型,输电网是MIP模型,均能采用商业优化求解软件如CPLEX进行求解,求解流程如图2所示。

图2 输配电网协调规划模型求解流程Figure 2 Flow chart for solving the coordination planning model of transmission and distribution network
模型的求解步骤如下:
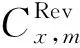
3)基于配电网的优化结果,将不同配网项目数对应的配网净收益以及新增配网负荷作为输电网规划模型的输入参数;4)根据配电网传入参数求解输电网规划模型,得到经输电网模型筛选后的配网项目投资方案,输电网的扩展方案。
4 算例分析
本算例将基于标准节点系统构造输、配电网协同规划问题,并利用本文提出的双层规划模型对其进行优化分析,进一步验证本文所提规划方法的有效性和合理性。数学优化求解器采用CPLEX 12.6。
4.1 基础数据
输电网采用Garver’s 6节点系统进行模拟,系统结构见文献[1]。系统中机组和线路的相关基本参数(线路物理参数有适当调整,线路成本已折算到日)如表1、2所示。

表1 Garver’s 6节点系统中的机组参数Table 1 Unit parameters of Garver’s 6 bus system

表2 Garver’s 6节点系统中的线路参数Table 2 Line parameters of Garver’s 6 bus system
输电网第4、5节点挂接的配电网均采用REDS-135节点模型,模型结构见文献[22]。节点4对应配网将原始的REDS-135模型中的10个节点作为拟建项目节点,10条线路作为备选线路,具体信息如表3、4所示;同样地,节点5对应配网的拟建项目节点和备选线路信息如表5、6所示。
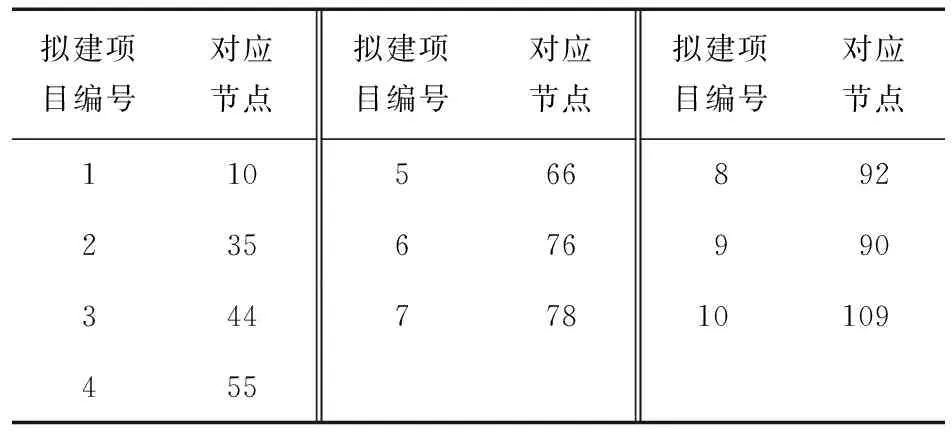
表3 节点4对应配网的拟建项目信息Table 3 Planning project information of distribution network corresponding to node 4
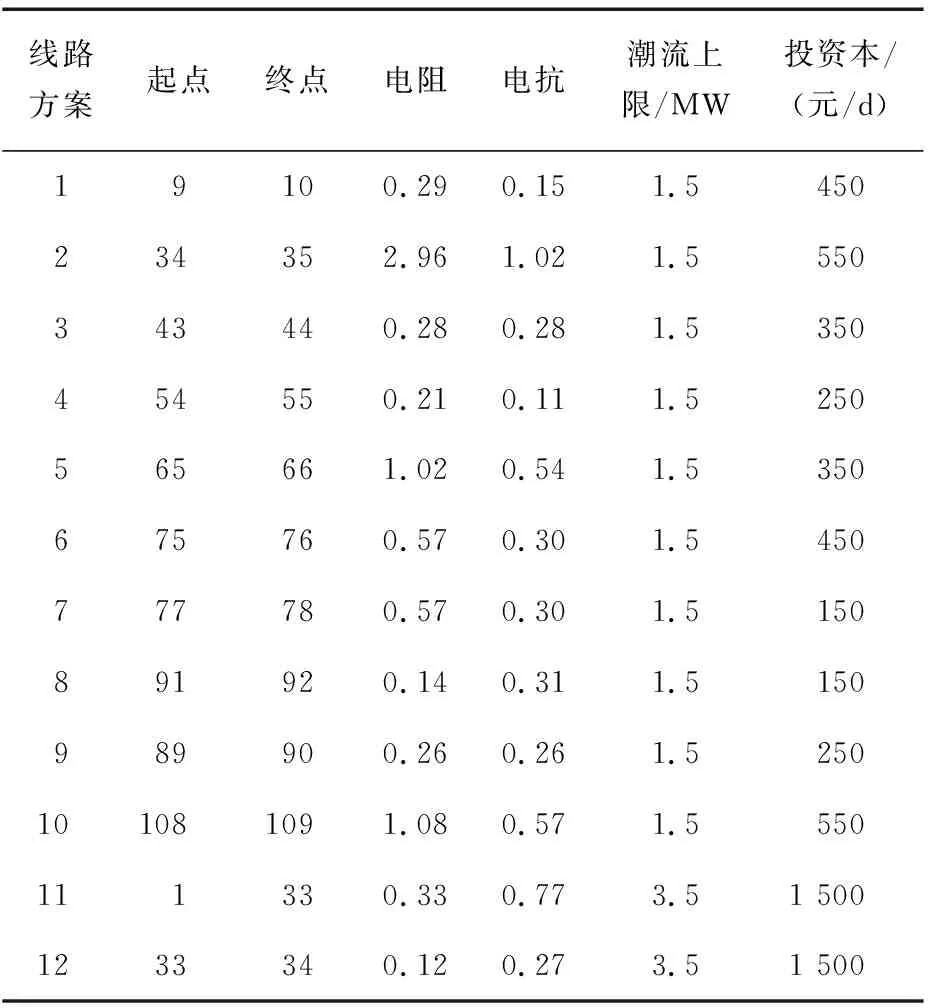
表4 节点4对应配网的备选线路信息Table 4 Candidate line information of distribution network corresponding to node 4
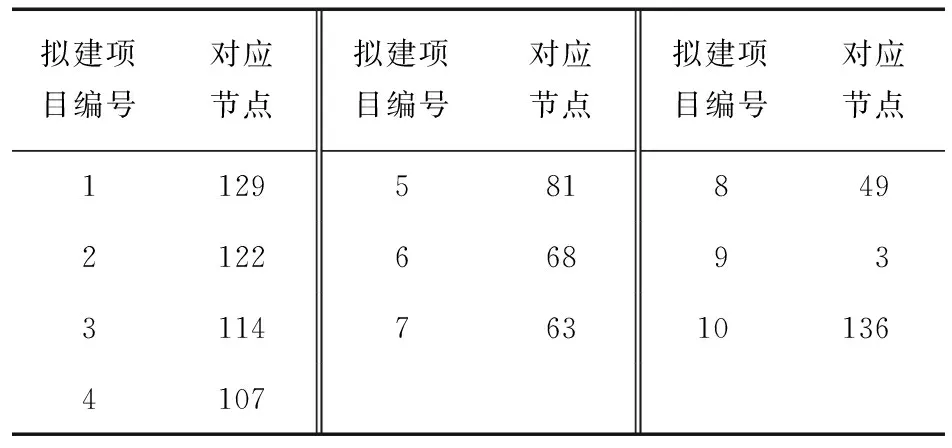
表5 节点5对应配网的拟建项目信息Table 5 Planning project information of distribution network corresponding to node 5
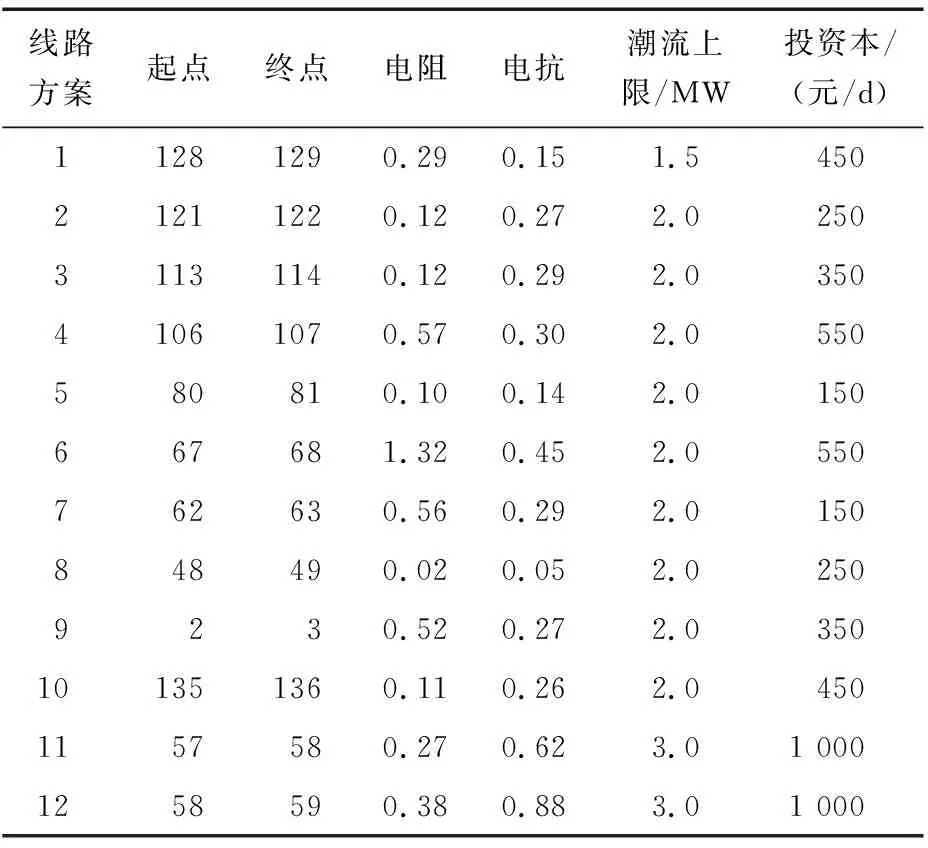
表6 节点5对应配网的备选线路信息Table 6 Candidate line information of distribution network corresponding to node 5
4.2 结果分析
4.2.1 配网等值规划结果
基于本文所提的配电网规划模型,将新建项目总数分别设为1,2,…,10,然后逐个进行优化计算,得到节点4、5对应配电网的项目—净收益关系曲线,如图3、4所示。
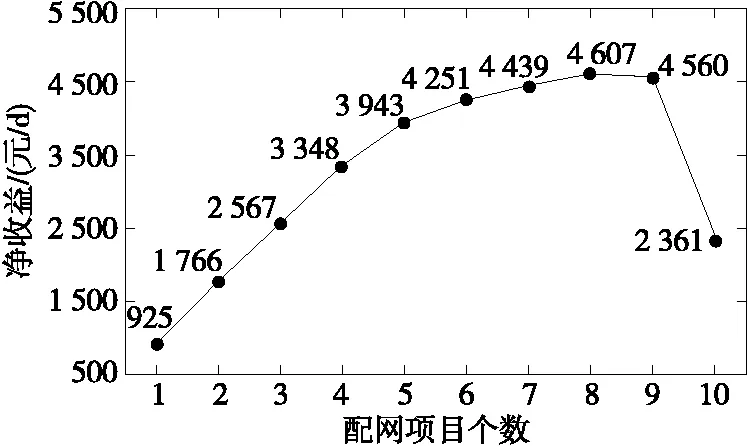
图3 节点4对应配网的规划等值曲线Figure 3 Planning equivalent curve of distribution network corresponding to node 4
比较图4、5可以发现,随着配网投建项目数的增加,配网净收益呈现出先增加后减小的趋势。这是因为待规划的初始配电网通常具有一定的容量裕度,当配网投建项目较少时,新增负荷也较少,配网线路能够满足新增负荷安全传输的需求,因而无需投资新建配网线路。配网售电收益增量为(售电电价-购电电价)×配网项目负荷增量。随着项目数的增加,配网净收益(售电收益-新建线路投资成本)必然随之增加;当配网投建项目增多到一定数量时,原有配网线路将无法满足新增负荷安全传输的需求,此时要投资新建配网线路。从短期来看,负荷增量引起的线路投资成本大于负荷增量带来的售电收益,导致配网净收益大幅下降。
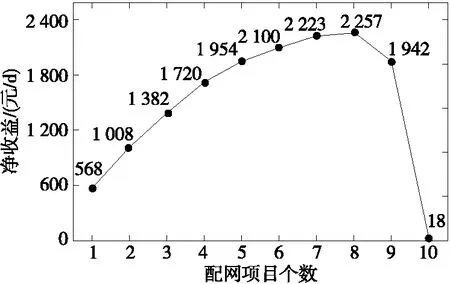
图4 节点5对应配网的规划等值曲线Figure 4 Planning equivalent curve of distribution network corresponding to node 5
4.2.2 输电网优化结果
将配电网规划模型得到的各配网新增负荷、投资和收益传递至输电网规划模型中,同时将所有配网的投资总额上限设为4 000 元/d。通过输电网规划模型优化计算后,得到节点4、5对应的配网规划方案,如表7所示(表中“1”表示项目投建,“0”表示项目不投建)。

表7 节点4、5配网拟建项目的优化结果Table 7 Planning project optimization results of distribution network corresponding to node 4 and node 5
相应地,输电网线路的扩展方案为线路10(4→6)。输电网规划模型目标函数即输、配电网每日最大综合净收益为2 561.44 元/d。
5 结语
本文提出了一种输电网和配电网协调规划方法,分别基于DistFlow、直流潮流方程建立了输电网和配电网规划模型,并通过配网规划等值曲线协调输电网和配电网规划问题,以提高输配电网联合规划的求解效率。基于Garver’s 6节点输电系统和REDS-135节点配电系统构造的输配电网协同规划算例对本文所提模型和方法进行了验证和分析。算例结果表明,所提出的配网规划等值曲线不仅能明确地表征配网投资项目数量和配网净收益的对应关系,还有助于减少输电网规划模型的变量规模,进而大大提升模型整体的求解效率。希望本文能为新电改背景下各级电网的协调规划决策提供有益参考。

