以“式”定法，巧妙解题

文／郭永胜

我们经常会遇到“判断二次函数的图像与坐标轴公共点的个数”这类问题。本文梳理了解决这类问题的一些方法，希望对同学们有所帮助。

一、基于一般式，关注通法

例1已知二次函数y=x2+（m-3）x+1-2m。试问此二次函数的图像与x轴有两个交点吗？为什么？

【解析】解决二次函数图像与x轴的交点问题，最直接的方法是根据二次函数y=ax2+bx+c（a、b、c为常数，且a≠0）与对应的一元二次方程ax2+bx+c=0之间的关系，将证明二次函数图像与x轴有两个交点转化为证明Δ=b2-4ac＞0，将“形”的问题转化为“数”的问题来解决。

令y=0，则x2+（m-3）x+1-2m=0，

∴b2-4ac=（m-3）2-4（1-2m）=m2+2m+5=（m+1）2+4。

∵（m+1）2≥0，

∴（m+1）2+4＞0。

∴该方程有两个不相等的实数根。

∴不论m为何值，该二次函数图像与x轴有两个交点。

【反思】利用一元二次方程根的判别式判断二次函数图像与x轴的交点个数，是解决这类问题的通法。该方法的关键是要将二次函数表达式写成一般式y=ax2+bx+c（a、b、c为常数，且a≠0），再准确地表示出根的判别式b2-4ac，有时需利用配方法，方便判断b2-4ac的符号。

二、基于交点式，精确计算

例2已知二次函数y=2（x-1）（x-m-3）（m为常数）。试问不论m为何值，该函数的图像与x轴总有公共点吗？为什么？

【解析】刚接触此题时，多数同学会想到用根的判别式进行判断，将二次函数整理为一般式y=2x2-2（m+4）x+2（m+3），再计算b2-4ac=4（m+2）2≥0，问题虽然得到解决，但计算过程过于烦琐。仔细观察不难发现，题目中给出的是二次函数的交点式，可以直接求出二次函数图像与x轴的交点坐标，从而解决问题。

令y=0，则2（x-1）（x-m-3）=0。

解得x1=1，x2=m+3。

当m+3=1，即m=-2时，方程有两个相等的实数根；

当m+3≠1，即m≠-2时，方程有两个不相等的实数根。

∴该方程总有实数根。

∴不论m为何值，该函数的图像与x轴总有公共点。

【反思】一般地，若二次函数y=ax2+bx+c（a、b、c为常数，且a≠0）的图像与x轴的交点横坐标为x1、x2，可把函数写成交点式y=a（x-x1）（x-x2）（a≠0）。判断二次函数图像与x轴的交点个数，虽然没有要求计算点坐标，但题目中给出的是二次函数的交点式，容易求出交点坐标，借助分类讨论使交点个数一目了然。对比用根的判别式，计算得到了极大的简化。

变式1已知二次函数y=a（x-m）2-a（x-m）（a、m为常数，且a≠0）。试问不论a与m为何值，该函数的图像与x轴总有两个公共点吗？为什么？

【解析】受到例2方法的启发，仔细观察式子，我们发现存在公因式a（x-m），故可将函数表达式进行因式分解，转化为交点式，从而得到与x轴的交点坐标。

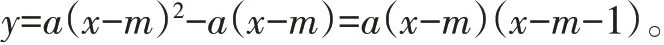
令y=0，则a（x-m）（x-m-1）=0。

∵a≠0，∴解得x1=m，x2=m+1。

∵m≠m+1，

∴方程有两个不相等的实数根。

∴不论a与m为何值，该函数的图像与x轴总有两个公共点。

三、基于顶点式，运用图像与性质

例3已知二次函数y=x2+2mx+m2-1（m为常数）。试问不论m为何值，该函数的图像与x轴总有两个公共点吗？为什么？

【解析】该函数表达式中存在完全平方式，故可以将表达式转化为顶点式y=a（x-h）2+k（a≠0），明确了开口方向和顶点纵坐标，借助函数图像和性质，画出草图，即可得证。

y=x2+2mx+m2-1=（x+m）2-1，则顶点坐标为（-m，-1），故顶点在x轴的下方。

∵a=1＞0，

∴函数图像开口向上。

依据性质，画出草图，可以直接看出函数图像与x轴总有两个交点。

【反思】一般地，二次函数y=a（x-h）2+k（a≠0）的顶点坐标为（h，k），根据函数图像的开口方向和顶点纵坐标k的正负（当k＞0，顶点位于x轴的上方；当k=0，顶点在x轴上；当k＜0，顶点位于x轴的下方），画出大致图像，即可确定函数图像与x轴的交点个数（如表1）。

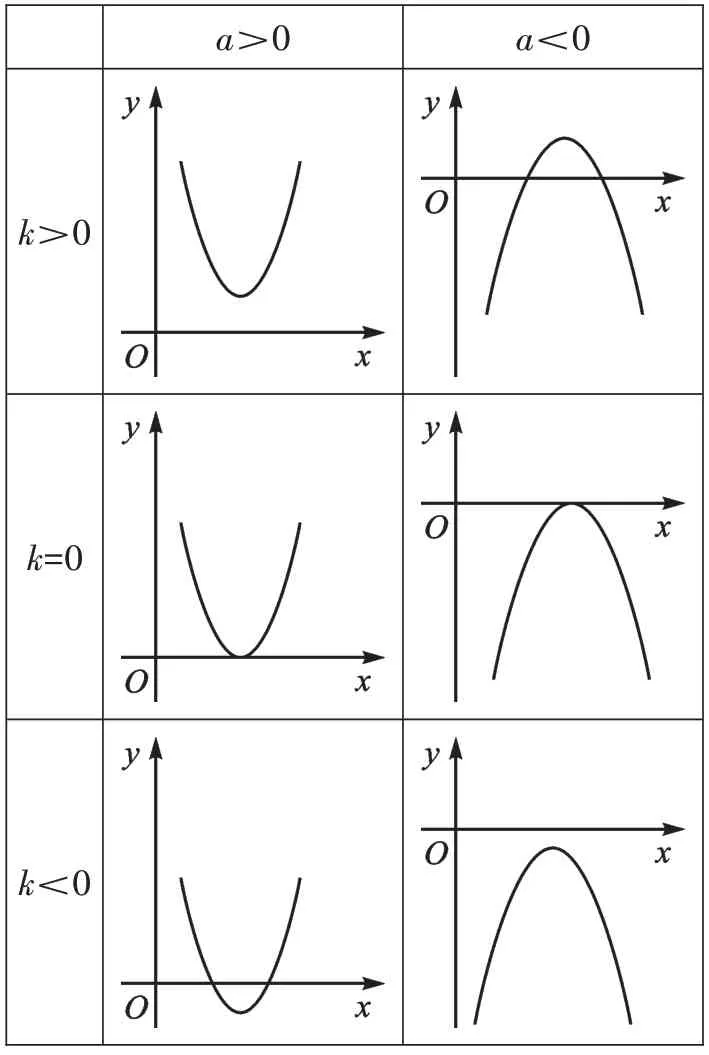
表1

变式2把二次函数y=x2+4x+m的图像向上平移1个单位长度，再向右平移3个单位长度，如果平移后所得抛物线与坐标轴有且只有一个公共点，那么m应满足条件___。

【解析】本题涉及二次函数图像的平移，可先将函数转化为顶点式，由平移规律写出新函数表达式。新函数图像与坐标轴只有一个公共点，一定在y轴上，且与x轴没有公共点，结合上表可得新函数的顶点纵坐标一定大于0。

y=x2+4x+m=（x+2）2+m-4，将图像向上平移1个单位长度，再向右平移3个单位长度，得新函数y=（x+2-3）2+m-4+1=（x-1）2+m-3。

由函数的性质可知，抛物线开口向上，且对称轴为直线x=1。

∵平移后所得抛物线与坐标轴有且只有一个公共点，

∴m-3＞0。

∴m＞3。

二次函数既有数的抽象，又有形的直观，是渗透数形结合思想方法的重要载体。我们既要会从数的角度计算，建立与方程、不等式的联系；又要会从形的角度分析，抓住函数图像的性质特征。希望同学们在学习二次函数时，深入理解三种表达式的特征和优点，并能熟练地相互转化，找到解决问题的最优形式，使解答过程更加顺畅。