二次函数中不等关系的解法

文／丁旭东

对于一次函数中的不等关系，很多同学可以利用解一元一次不等式的方法来解决问题。而对于二次函数中的不等关系，同学们肯定也想通过类比之前的学习，用解一元二次不等式的方法来解决问题，但发现略显困难，这便需要利用二次函数的“辅助功能”。

一、给定x或x的范围，确定y的大小关系

1.两点在对称轴的同侧时

当两点在对称轴同侧时，我们只需根据函数的增减性即可判断函数值的大小。

例1已知抛物线y=-（x+2）2上的两点A（x1，y1）和B（x2，y2），如果x1＜x2＜-2，那么下列结论一定成立的是（ ）。

A.0＜y2＜y1B.y1＜y2＜0

C.0＜y1＜y2D.y2＜y1＜0

【解析】抛物线的对称轴为直线x=-2，抛物线开口向下，函数在x＜-2时，y随x的增大而增大，

∴y1＜y2，而y=-（x+2）2≤0，

∴y1＜y2＜0。故选B。

2.两点在对称轴的异侧时

当两点在对称轴异侧时，我们可以利用二次函数的轴对称性，把异侧两点转化为同侧，也可以利用与对称轴距离的远近来确定函数值的大小。特别要注意的是，当顶点在区间内，顶点的值就是最值。

例2已知二次函数y=（x-2）2-2，关于该函数在-1≤x≤3的取值范围内，下列说法正确的是（）。

A.有最大值-1，有最小值-2

B.有最大值0，有最小值-1

C.有最大值7，有最小值-1

D.有最大值7，有最小值-2

【解析】抛物线的对称轴为直线x=2，且开口向上，所以当x=2时，y有最小值-2。点（3，y1）的对称点为（1，y1），根据二次函数性质，在对称轴左侧，y随x的增大而减小，所以当x=-1时，y有最大值7。我们还可以观察图像，发现在取值范围内，表示x=-1的点离对称轴直线x=2最远，所以当x=-1时，y有最大值7。故选D。

3.利用图像与x轴的交点坐标，确定交点两侧相应y的大小

设二次函数y=ax2+bx+c（a、b、c为常数，且a≠0）与x轴的交点坐标为（x1，0）、（x2，0）（x1＜x2）。

若a＞0，则当x＜x1或x＞x2时，y＞0，当x1＜x＜x2时

若a＜0，则当x＜x1或x＞x2时，y＜0，当x1＜x＜x2时

例3对称轴为直线x=1的抛物线y=ax2+bx+c（a、b、c为常数，且a≠0），如图1所示，某同学得出了以下结论：①4a+2b+c＞0；②9a+3b+c＞0；③a+b≤m（am+b）（m为任意实数）。其中结论正确的个数为（ ）。

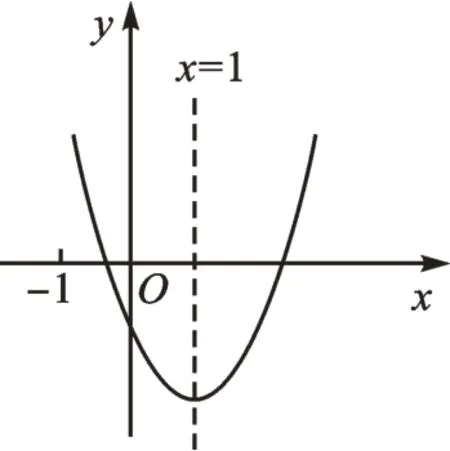
图1

A.0 B.1 C.2 D.3

二、给定y或y的范围，确定x的大小关系

【解析】当x=0时，y＜0。抛物线的对称轴为直线x=1，根据图像可知，抛物线与x轴的右边交点横坐标x的范围是2＜x＜3。

∴当x=2时，y＜0，即4a+2b+c＜0，结论①不正确；

当x=3时，y＞0，即9a+3b+c＞0，结论②正确。

∵抛物线开口向上，抛物线的对称轴为直线x=1，

∴当x=1时，y取得最小值，最小值为y=a+b+c。

∴对于任意实数m，有am2+bm+c≥a+b+c。

∴a+b≤m（am+b）（m为任意实数），结论③正确。

故选C。

我们可以利用二次函数图像与x轴、直线、双曲线等的交点坐标，解决一元二次不等式问题。结合图像，数形结合，通过交点坐标（x0，y0）推断x=x0时，y1=y2=y0，从而以x0为分界线，对比y1与y2的大小关系，确定x＜x0还是x＞x0，从而可以解决相关不等式ax2+bx+c＞0（或ax2+bx+c＜0），ax2+bx+c＞m（或ax2+bx+c＜m），ax2+bx+c＞kx+b（或ax2+bx+c＜kx+

b），ax2+bx+c＞（或ax2+bx+c＜）的解集问题。

例4如图2，二次函数y1=x2+mx+1的图像与y轴相交于点A，与反比例函数的图像相交于点B（3，1）。当y1随x的增大而增大且y1＜y2时，写出x的取值范围。

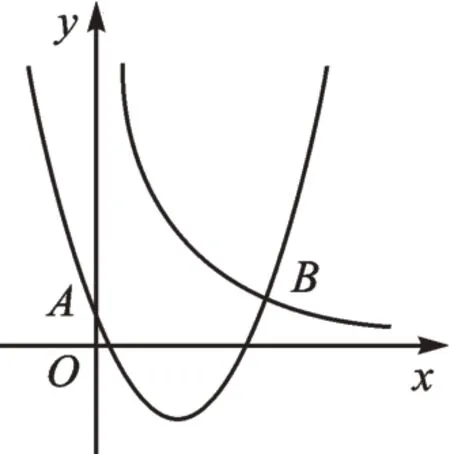
图2

【解析】将点B（3，1）代入二次函数表达式，得m=-3，即y1=x2-3x+1，∴对称轴为直线由图像知，当y1随x的增大而增大且y1＜y2时

三、给定x在某范围内y的值，确定参数的值

此时要确定对称轴的位置，针对对称轴不同的位置，分类讨论确定哪一个点的函数值是对应y的值，得到关于参数的方程，从而求解。

例5已知二次函数y=x2+ax+3，当-1≤x≤6时，函数y的最大值为8，求a的值是否存在。

【解析】∵二次函数y=x2+ax+3

∴二次函数的对称轴为直线①当，即a≤-12时，此时二次函数在-1≤x≤6范围内，y随x的增大而减小，在x=-1处取最大值，即1-a+3=8，解得a=-4，与a≤-12不符；

②当，即-12＜a≤-5时，此时x=-1离二次函数对称轴更远，

∴二次函数在x=-1处取最大值，即1-a+3=8，解 得a=-4，与-12＜a≤-5不符；

③当，即-5＜a≤2时，此时x=6离二次函数对称轴更远，

∴二次函数在x=6处取最大值，即36+6a+3=8，解得，与-5＜a≤2不符；

④当，即a＞2时，此时二次函数在-1≤x≤6范围内，y随x的增大而增大，在x=6处取最大值，36+6a+3=8，解得，与a＞2不符。

综上所述，不存在符合题意的a的值。