误差有界的低扭曲非结构T样条曲面拟合

关启超，刘 浩，王远成，傅孝明

误差有界的低扭曲非结构T样条曲面拟合

关启超，刘 浩，王远成，傅孝明

(中国科学技术大学数学科学学院，安徽 合肥 230000)

为了计算对于任意复杂拓扑拟合域的低扭曲、满足拟合误差阈值和较少控制点的非结构T样条拟合曲面，提出了一种逐步求解的方法。首先，生成与拟合域具有相同拓扑的多立方体作为参数域，通过多次重参数化过程优化待拟合表面和参数域之间的对应关系，得到一个适用于获得低拟合误差样条曲面的低扭曲映射。与此同时，利用非结构T样条局部细分的性质对不满足拟合误差阈值的区域进行自适应局部细分，得到满足拟合误差阈值的低扭曲样条曲面。接下来，提出一种删除冗余控制顶点的拟合曲面简化策略，在满足拟合误差阈值和低扭曲的基础上删除冗余的控制顶点，得到控制顶点数量较少的误差有界的低扭曲非结构T样条拟合曲面。在各种复杂模型上证明了此方法的有效性。与最新的方法相比，该方法以更少的控制顶点实现了更低的参数化扭曲。

低扭曲；非结构T样条；曲面拟合；多立方体参数域；局部细分

随着计算机造型设计技术和三维采集技术的发展，海量的三维几何模型应运而生，然而这些模型很少能够直接用于实际应用，包括逆向工程、3D建模和3D打印。只有经过转换，其才能在实际应用中更容易地进行二次编辑。由于样条曲面具有参数方程和高阶连续性，且表示方法更紧凑，使得样条曲面在造型设计中更有利于光滑形状的描述和分析。因此，在计算机辅助设计与制造工业和工程计算中，经常需要使用样条曲面拟合技术将输入的离散数据转换成易于编辑的样条曲面。

样条曲面拟合的目标是构造一个样条曲面与输入的离散数据的拟合误差小于给定的阈值，并尽可能使得拟合曲面的扭曲较低、控制点数量较少。首先，如果样条曲面与输入模型之间的拟合误差越小，对原模型细节的保留就越多。其次，拟合结果的扭曲越低，对拟合曲面进行二次设计越容易、操作越简单，同时使得数值模拟精度越高。最后，由于较多的控制顶点不仅会占用更多的内存空间，还提高设计师对于拟合曲面进行二次设计的难度，因此希望使用较少的控制顶点表示拟合曲面。

然而，求解满足上述3个目标的样条曲面是非常具有挑战的，理由有3个：①给定任意复杂拓扑的模型，生成合适的样条参数域满足上述要求是非平凡的；②参数域和输入模型之间的对应与近似误差和扭曲之间是非线性关系，求解一个适用于获得低近似误差、低扭曲的对应是困难的；③控制顶点的数量与低拟合误差和低扭曲是矛盾的，低拟合误差和低扭曲需要较多的控制顶点。

现有方法都不能很好地解决上述问题。通用的方法是将输入模型分割为多个较小的子面片，并对每个子面片独立求解，最后将所有子面片拼接在一起[1-2]。虽然在每个子面片上均能得到满意的结果，但是将子面片拼接在一起时为了保证连续性和拟合误差，不可避免会增加控制顶点的数量。为了降低样条曲面的控制顶点，有学者提出使用T样条曲面进行拟合[3-5]，T样条允许自适应局部细分，只对拟合结果不满意的区域进行精细拟合，在处理细节分布不均匀的复杂模型时具有很大的吸引力。但是上述方法要么对输入模型的拓扑有限制，要么没有显式的建立降低扭曲的优化模型，均无法得到满足上述3个目标的样条曲面。

本文提出了一种非结构T样条曲面拟合算法，对任意亏格的输入模型均得到满足拟合误差的低扭曲的样条曲面，并显著减少了控制点的数量。采用逐步求解的策略依次满足3个目标。给定一个任意复杂拓扑的模型，使用与输入模型具有相同拓扑的多立方体作为参数域，并通过同时优化内部和边界来生成一个低扭曲的体映射，从而获得低扭曲的拟合函数。接下来，为了使得拟合误差小于给定的阈值，利用非结构T样条的局部细分的性质对不满足拟合误差的区域进行了自适应局部细分。这时候，控制顶点的数量往往较高。为此，本文提出一种拟合曲面简化策略，在满足拟合误差和低扭曲的基础上逐点的删除冗余控制顶点。

本文方法对于任意复杂拓扑的输入模型均能得到低扭曲拟合曲面，并且在具有145个复杂模型的数据集上验证了可行性和有效性。与最新的方法相比，本文方法使用更少的控制顶点实现了更低的参数化扭曲。

1 相关工作

样条曲面在计算机辅助设计与制造中有着广泛地应用，非均匀有理B样条已经成为行业标准。通过对结点向量的细化和控制点的调整，其可以用来表示任意复杂的曲面。有许多学者使用B样条或NURBS曲面拟合复杂模型[6-9]。然而，由于这种张量积曲面表示要求控制网格的每一行和每一列都有相同数量的控制点，但只允许所谓的结点向量的全局细化，往往导致在表示复杂模型时出现许多冗余控制点，从而降低拟合速度和后续许多操作的效率[10-11]。

为解决上述问题，SEDERBERG等[11-12]提出T样条。通过在控制网格中允许T节点的存在，实现了局部细分，避免了多余的控制点。每次插入一个控制点时，只需要引入少量的相邻控制点，而无需整行或整列地增加控制点。局部细分简化了曲面的表达式，节省了存储空间，相比于NURBS，更适合进行曲面拟合。

T样条拟合方法首次由ZHENG等[13-14]提出，即利用T样条重构光滑参数曲面的自动算法。该算法从粗糙表面近似开始，然后在近似精度不满足要求的区域逐步细化。根据输入数据的局部几何特征自适应地确定生成的T样条曲面的拓扑，并通过最小二乘法获得控制点的几何。除此之外，还提出了几种新的可用于增强拟合算法的即插即用组件或策略[3]：使用T样条进行拟合、曲率引导策略、合适的重新参数化和初始样条节点重置，并利用这些组件和策略又提出了一种集成这些组件和策略的自适应T样条拟合算法。

在YANG和ZHENG[15]的工作中，提出了一种T样条曲面蒙皮算法，该算法生成一个T样条曲面，可以独立构造样条曲面的截面曲线和控制曲线，并在相同拟合误差阈值的情况下生成的样条曲线通常比传统放样样条曲线具有更少的控制点。LIN和ZHANG[16]提出了一种渐进式T样条数据拟合算法，用于拟合具有T样条表示的大型数据集。作为一种迭代方法，其迭代速度稳定，对未知T网格顶点数量的增加不敏感，因此能够有效地拟合大型数据集。

上述方法均未得到低扭曲、低拟合误差且删除冗余控制顶点的T样条拟合曲面，而本文方法得到了满足此目标的拟合曲面，并且使用更少的控制顶点实现了更低的参数化扭曲。

2 方 法

2.1 方法概述

2.1.1 问题概述

本文研究误差有界的低扭曲非结构T样条曲面拟合问题。输入为任意复杂拓扑的三角网格拟合域和拟合误差，其中拟合域包含一组顶点={v}和一组三角形面={f}。其目标是计算一个非结构T样条曲面满足以下条件：

(1) 拟合曲面与拟合域之间的拟合误差小于；

(2) 拟合曲面的扭曲较低；

(3) 拟合曲面的控制点数量较少。

2.1.2 非结构T样条

T样条的一般表达为

其中，P为控制点，w为权重；B(,)为T样条混合基函数，其表达式为

其中，[u]()和[v]()均为三次B样条基函数，即

非结构T样条是传统T样条的推广，通过向网格中添加奇异点使得样条具有更强的表达能力。记网格中每个节点连接边的数目为该节点的度()，()≠4且不为T节点的节点称为奇异点。

一个非结构T样条的参数域必须满足以下3个规则：

规则1.一个面内相对的2个边上的节点间隔必须相等；

规则2.如果一个面相对的2个边上都有T节点，且将其连接起来不违反规则1，那么这2个T节点必须用边连接起来；

规则3.奇异点的2领域面内不能有其他奇异点或者T节点。

前面2个规则是T网格的规则，第3个规则是针对奇异点的处理，目的是方便计算奇异点2领域内的基函数。

真实的参数域无法在平面上绘制出来，图1给出了一个非结构T样条参数域拓扑，其中，中间的点表示()=3的奇异点，阴影区域表示奇异点的2领域。

图1 非结构T样条参数域拓扑[17]

与T样条相似，在得到非结构T样条的定义域之后，需要给出每个顶点上的混合函数，每个混合函数通过该顶点进行局部定义。根据T样条混合函数的定义方法，如果一个区域可以将其邻域无扭曲的参数化到平面上，就可以应用平面的T网格定义的方法来定义空间区域的T样条。如图1中不在阴影区域上的顶点。对于这些顶点，首先需将其局部无扭曲的参数化到平面，定义基函数后可以直接映射回多立方体参数域[17]。

对于奇异点2领域内的顶点，本文使用SCOTT等[18]提出的方法计算每个顶点上的混合函数。

2.1.3 多立方体参数域

为了避免因对复杂拓扑形状进行分割和拼接而造成的控制点数量的增加，得到全局统一的样条表达，本文使用多立方体作为实现样条拟合曲面的参数域，记为。多立方体提供了一种矩形结构，可以正确表示任意几何形状的拓扑，而奇异点只在角点处出现，非常有利于后续的计算和分析。

最初始的多立方体参数域除去需要满足多立方体的条件之外，还需额外满足非结构T网格的3个条件。对于任意生成的多立方体形状，只需对所有面执行2次细分，就可以得到满足要求的多立方体参数域，在本文的算法中，初始多立方体参数域的选择不会影响最终的拟合精度。

2.1.4 问题挑战

如前所述，求解满足上述3个目标的样条曲面是非常具有挑战的。可将计算目标样条曲面表述为以下优化问题

其中，E()为映射的扭曲能量；E()为()与之间的拟合近似程度能量；E()为样条曲面简化程度能量；和为2个正的权重，用来平衡扭曲能量、近似程度能量和简化程度能量。

求解此优化问题是一项非常具有挑战性的事情。第一，很难定义一个适用于优化扭曲的近似程度能量和简化程度能量。第二，由于控制顶点的数量与低拟合误差和低扭曲是矛盾的，因此很难定义权重和的大小。第三，该优化问题非凸非线性，在保持拟合误差较低的情况下高效地优化扭曲是一件非常困难的事情。

2.1.5 求解思路

针对上述挑战，考虑到非结构T样条具有局部细分的能力，将计算满足上述目标的样条曲面分为以下3个步骤：

步骤1.计算一个低扭曲的拟合映射，此时不一定满足拟合误差；

步骤2.在不满足拟合误差阈值的区域进行自适应局部细分；

步骤3.在满足拟合误差和低扭曲的基础上删除冗余的控制顶点，简化拟合曲面。

用图2例子来说明本文求解低扭曲非结构T样条曲面的重参数化-拟合步骤。其中黄色表示不满足拟合误差阈值的区域。

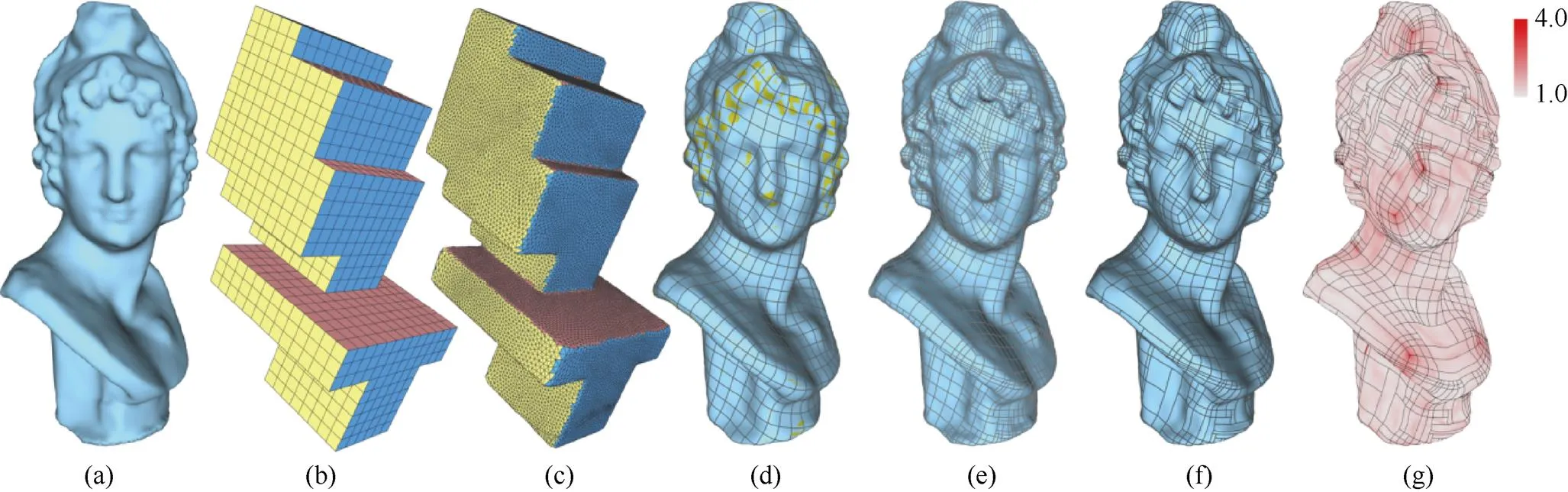
图2 本文系统概览((a)输入；(b)与输入网格具有相同拓扑的多立方体参数域；(c)输入网格参数化到多立方体参数域；(d)拟合结果；(e)自适应局部加细结果；(f)自适应简化结果；(g)最终结果和扭曲)

2.2 低扭曲拟合

给定一个任意复杂形状的模型。其生成与输入模型具有相同拓扑的多立方体作为参数域，并通过多次重参数化过程优化待拟合表面和参数域之间的对应关系，在满足边界约束的条件下得到扭曲较低的映射。接下来，利用低扭曲映射的逆映射来拟合样条曲面，得到低扭曲且光滑的样条曲面。

2.2.1 计算低扭曲参数化

本文需要找到一个有利于拟合操作的低扭曲的表面映射。HU等[19]指出，传统的平面能量可导致扭曲分布的不均匀，映射后得到狭长的三角形，不利于拟合操作，于是提出使用体能量来驱动等距优化。LIU等[20]使用内部和边界共同优化的体能量来获得低扭曲体参数化结果。同样的，本文将拟合网格映射到多立方体参数域中，使用内部和边界共同优化的体能量来获得低扭曲的表面映射。

其中，E为三维扭曲能量，该能量限制在边界上是边界扭曲能量。

本文使用FU等[22]提出的AMIPS能量和文献[20]提出的方法将边界映射限制在参数域边界上的硬约束转换为每个边界顶点在切空间移动的软约束，然后使用文献[20]的内部和边界共同优化方法来获得低扭曲体参数化映射。

2.2.2 非结构T样条拟合

本文使用非结构T样条拟合输入的拟合域，一种常用的方法是最小化插值拟合。此外，为了生成视觉上的光滑曲面，经常需要在目标函数中添加光滑函数项。此时，优化问题变成最小化目标函数

其中，E为拟合误差项；E为光滑能量项；为一个权衡常数。

本文使用一个双向的能量来表示2个曲面上的采样误差

其中，第一项是插值误差，(v)称为v对应的参数；第二项是采样拟合误差，u是参数域中的采样点。在实验中，采样点是每个参数域面中的高斯节点。

第二项光滑能量项的具体表达为

其中，为在局部参数坐标系中沿方向的二阶导数。

T网格样条的导数为节点函数导数的线性组合，由于在拟合过程中基函数是固定的，2个能量都可以表述为未知控制点的二次函数，可以通过求解一个线性方程组得到解。

如图3所示，对于图3(a)中复杂拓扑的模型，使用本文方法得到图3(b)所示的低扭曲、光滑的样条曲面，其中黄色表示不满足拟合误差阈值的区域，图3(c)为样条曲面扭曲分布图，平均扭曲为1.208。从图中可以看出，只有很小部分违反拟合误差的约束。下一阶段的目标是降低最大拟合误差。

图3 低扭曲拟合曲面结果图((a)输入；(b)低扭曲、光滑的样条曲面；(c)扭曲)

2.3 降低拟合误差

由于T样条具有自适应局部细分能力，可以在拟合结果不令人满意的区域进行精细拟合，此方法显著地减少计算量，降低计算成本。

本文通过最大拟合误差来控制拟合的精度，即

考虑一个参数域中的矩形域，如果存在映射在中的原网格点v或有采样点u违反约束，则对R进行细分。

在自适应细化之后，需要重新计算拟合方程并更新控制点。本文重复执行自适应细化过程直到满足拟合误差。

如图4所示，对于图4(a)中不满足拟合误差阈值的区域，采用自适应局部细分进行精细拟合，得到图4(b)满足拟合误差的结果。图4(c)为样条曲面扭曲分布图，平均扭曲为1.247。从图中可以看出，本文方法在低扭曲的条件下只在不满足拟合误差阈值的区域进行局部细分，显著地减少了计算量。但此时控制顶点的数目较多，下一阶段的目标是删除冗余的控制顶点，简化样条曲面。

图4 降低拟合误差结果图((a)拟合曲面；(b)自适应加细结果；(c)扭曲)

2.4 简化曲面

由于删除一个节点之后，需要重新计算拟合方程并更新控制点，所以无法同自适应局部细分一样，在一次循环过程中判断所有采样点，对所有满足条件的区域均进行简化操作。此时，本文提出一种逐点简化策略，在满足拟合误差和低扭曲的基础上逐点地删除冗余控制顶点。

算法步骤如下：

输入：满足拟合误差阈值和低扭曲的T样条曲面。

输出：简化后的满足拟合误差阈值和低扭曲的 T 样条曲面。

步骤1.记样条曲面的平均扭曲为_，=1.1×_。

步骤2.记多立方体参数域节点个数为，取=0。将T网格上每一个节点均作为采样点，计算拟合误差||(u)–(u)||2，并排序，记为一个优先队列，使得(0)为最小值。

步骤3.若=，算法结束，否则执行步骤4。

步骤4.判断()所对应的节点是否可以删除。

步骤5.删除该节点，重新计算拟合方程并更新控制点，返回步骤2。

如图5所示，图5(a)是2.3节得到的满足拟合误差的低扭曲样条曲面，此时控制顶点的数量为4 880；图5(b)是使用简化策略得到的样条曲面，此时样条曲面同样满足拟合误差阈值和低扭曲条件，控制顶点的数量为3 038；图5(c)为样条曲面扭曲分布图，平均扭曲为1.346。本文的简化策略在满足低拟合误差和低扭曲的基础上删除了1 842个冗余控制顶点，简化率为37.75%。

图5 简化前后样条曲面对比图((a)简化前样条曲面；(b)自适应简化结果；(c)扭曲)

2.5 实现细节与讨论

2.5.1 扭曲的选取

有多种扭曲能量可以被选择用于参数化，若选择共形扭曲，虽然可以很好地保持角度，但如果拟合域的模型中含有狭长的三角形，则可能会引起大的面积变形，不利于拟合操作，导致在变形较大的区域需要进行许多不必要的自适应局部细分才能满足拟合误差，对于本文的拟合方法，由于最关注的是边界的形状在优化扭曲的同时不会发生较大的变形，如果选择等距扭曲，可以在优化扭曲的同时保持角度和面积，使得输入拟合域的特征在参数域中均匀地分布，不会引起较大的变形，避免了在参数域中特征的集中分布而引起大量的自适应局部细分。因此，本文选择等距扭曲进行优化。

2.5.2 采样拟合误差的必要性

在使用非结构T样条拟合过程中，本文方法使用插值误差和采样拟合误差构造了一个双向能量。如果只使用插值误差能量，当网格质量很差时，即当输入网格比较稀疏时，参数域中的面可能没有对应的插值点，导致拟合矩阵可能是奇异的，从而导致插值拟合失败。尽管添加光滑项可以避免奇异问题，但会导致丢失拟合的细节。使用本文的双向能量构造的拟合矩阵可以避免奇异性，并且可以提高拟合精度。

2.5.3 优化扭曲的同时拟合样条曲面

求解低扭曲样条曲面拟合的一种可能方法是在每次迭代中同时更新控制点的位置和拟合样条曲面。此方法有一个主要限制：在优化扭曲更新控制点位置时，需要控制拟合误差在一定的范围内，否则较大的误差会导致较多的自适应细分才能满足给定的误差阈值，并且有可能无法保证双射的对应关系，对后续拟合过程带来困难。

2.5.4 自适应局部细分的同时简化拟合曲面

在构造低扭曲非结构T样条曲面之后，可以考虑在误差较大的区域进行自适应局部细分的同时在误差较小的区域简化拟合曲面。然而，此方法有一个较大的问题：在单次重新参数化-拟合迭代中对误差较小的区域进行了简化，删除了部分冗余的控制顶点。在下次重新参数化-拟合迭代过程中，由于在优化扭曲的过程中更新了顶点位置，在上次迭代过程中误差较小的区域此时可能误差较大，需要进行自适应局部细分，导致在同一个区域重复进行了自适应细分和删除冗余控制点的简化操作，增加了计算成本。

2.5.5 先构造简化样条曲面后优化扭曲

由于样条曲面简化策略是逐点判断的，并且在删除一个节点后需要重新计算拟合方程并更新控制点，计算成本高，此时可以考虑使用文献[12]的方法先构造满足误差约束的简化样条曲面，再更新顶点位置优化扭曲。但该方法存在一定的限制：更新顶点位置后样条曲面一般不满足误差约束，需要重新进行自适应局部细分和样条曲面简化，计算成本同样较高。

3 实验和比较

为了验证本文方法可以有效生成误差有界的低扭曲的简化样条曲面，进行了相关的实验。

3.1 与直接使用多立方体映射对比

绝大多数使用多立方体映射的目标是构建低扭曲的对应关系。其中，文献[21]通过基于旋转驱动的变形方法得到近似轴对齐形状，并利用近似轴对齐形状与多立方体结构之间的近似误差来代替等距扭曲度量，同时利用带约束的优化方法，生成与输入拟合域近似程度很高、且扭曲较低的多立方体映射。图6分别使用文献[21]多立方体映射和本文方法的平均扭曲分别为1.334和1.331，控制顶点的个数分别为1 116和915。可以看出，本文方法在相同拟合误差阈值的情况下得到了扭曲更低、控制顶点更少的拟合曲面。

图6 本文方法与文献[21]方法的对比结果((a)输入；(b)多立方体参数域；(c)文献[21]的方法；(d)本文方法)

3.2 数据集上的结果

本文使用()表示输入拟合域的网格顶点数目，()表示与拟合域具有相同拓扑的多立方体参数域的顶点数目，()表示自适应局部细分后样条曲面控制顶点的数目，()表示简化样条曲面控制顶点的数目，d(×10−3)给出了最大拟合误差，及平均扭曲、简化率、自适应细分迭代次数和奇异点数。

3.2.1 不同多立方体参数域比较

对于同一个输入的拟合域，本文使用不同的参数得到与给定拟合域具有相同拓扑的节点个数不同的多立方体参数域。不同的参数域的结果如图7所示，其中图7(a)表示输入的待拟合模型，图7(b)～(d)分别表示随着多立方体参数域节点个数的增加，所得到的自适应局部细分后满足拟合误差的低扭曲样条曲面和扭曲分布，以及简化的样条曲面和扭曲分布。其中参数域的节点个数、样条曲面的控制点数、简化样条曲面的控制点数、平均扭曲、简化率、自适应细分迭代次数、以及奇异点数见表1。

从表1可以看出，随着多立方体参数域慢慢逼近输入的拟合域，在相同拟合精度的情况下样条曲面的平均扭曲逐步降低，自适应细分迭代次数逐步减少，但样条曲面控制点的数量和奇异点数量逐步增加。

3.2.2 部分结果展示

本文在具有145个例子的数据集上测试了拟合的结果，全部得到了满足拟合误差的样条拟合结果，图8展示了数据集中的14个例子，每个例子给出了多立方体参数域、最终拟合结果扭曲分布图和误差分布图，其中误差分布图中黄色区域表示非结构T样条拟合曲面与拟合域之间的误差趋于拟合误差阈值的区域。表2给出了相关例子实验结果，从结果可以看出，对于给定模型和拟合误差阈值，本文方法均得到低扭曲的简化样条曲面。

图7 不同的多立方体参数域((a)输入；(b)～(d)多立方体参数域、自适应加细的样条曲面和扭曲、自适应简化的样条曲面和扭曲)

表1 不同的多立方体参数域的实验结果

图8 本文结果展示

表2 实验结果

3.2.3 运行时间分析

本文所有实验是在配备八核十六线程的英特尔酷睿 i7-4790K处理器和16 GB内存的台式电脑上运行的，处理器主频为2.50 GHz，使用Intel Math Kernel Library®进行方程求解。由于样条曲面简化策略是逐点判断，并且在删除一个节点后需要重新计算拟合方程并更新控制点，所以运行时间很长，其主要运行时间在简化样条曲面。在自适应局部细分过程中，一次迭代过程中对判断出大于拟合误差的区域同时细分，所以自适应局部细分次数较少，运行时间相对较少。在优化逆参数化时，相比立方体参数，多立方体参数域与拟合域较为相似，所以扭曲相对较低，运行时间同样相对较少。在表2中给出了整体的时间，其中约70%时间花费在最后的简化步骤中。可以看出运行时间主要受多立方参数域网格顶点数目和几何形状复杂程度影响，因为非结构样条的计算时间与参数域网格顶点数目正相关，所以多立方体数目越多，运行时间长；另一方面，几何形状越复杂，在删除操作时就越容易被拒绝，导致运行时间增长。

4 结束语

本文提出了一种通过多立方体参数域的重参数化-拟合方法来改进非结构T样条拟合结果的方法，可以对任意复杂拓扑的拟合域得到满足拟合误差阈值且低扭曲的简化样条曲面。此方法通过生成与给定拟合域具有相同拓扑的多立方体参数域，然后依次通过重新参数化、自适应局部细分、简化样条曲面策略，在包含145个例子的数据集上，均得到低扭曲的满足拟合误差阈值的简化的样条曲面。与直接使用多立方体参数域的映射结果相比，本文结果的扭曲更低，样条曲面的控制点更少。

本文方法未考虑具有特征的模型的输入，虽然保持了在所有的采样点均满足拟合误差阈值，但最终拟合结果会得到平滑的样条，未保留模型的某些需要的特征，如图9所示。T样条具有支持重节点的特性，一种可能的方法是利用重节点来定义特征。解决该问题的关键是将网格上的特征边参数化到参数域的边上，如何构建保持特征的参数化是值得考虑的问题。

图9 有特征的模型的结果

此外，本文方法还有一些可以改进的地方：

(1) 本文方法不能在优化扭曲过程中改变多立方体的形状，如前所述，与拟合域越接近的多立方体可以获得越低的扭曲，但代价是奇异点和拟合曲面控制点数量的增加，如何自适应的平衡控制点的数目和拟合的扭曲，是一个非常值得研究的问题。

(2) 所得到的拟合曲面虽然删除了冗余控制点，使T样条拓扑结构更加简洁，但计算成本较高，运行时间较长，主要时间花费在简化样条曲面。本文已经对简化算法进行了部分局部化，在删除一个顶点时，只重新计算局部的混合函数并进行拟合和距离检查。

但对不同点之间的删除判断进行并行计算存在一些困难，原因在于：尽管样条的基函数是局部的，但是每次删除顶点后，参数域的网格拓扑发生了改变，导致相关的混合函数都发生了改变，原本并行无关的点可能不再无关，这导致传统的并行方法不能直接应用到该问题上，并且T样条混合函数不具备完全统一的表达方法，也为并行带来了较大的难度。

不过本文观察到删除冗余控制点耗费的主要时间在距离检测上，并且此时所有T样条混合函数都是固定的，在该阶段应该可以设计合适的并行算法来提高效率。

另一方面，删除冗余控制点耗时较长的另一个原因是后期大量删除被拒绝，导致运行时间较长，如何设计一个更合理的待删除点的筛选算法也是一个值得研究的问题。

[1] LU Y, YONG J H, SHI K L, et al. B-spline surface fitting to mesh vertices[J]. Science China Information Sciences, 2017, 60(7): 078101.

[2] BERTOLINO G, MONTEMURRO M, PERRY N, et al. An efficient hybrid optimization strategy for surface reconstruction[J]. Computer Graphics Forum, 2021, 40(6): 215-241.

[3] WANG Y M, ZHENG J M. Curvature-guided adaptive T[J]. Computer-Aided Design, 2013, 45(8-9): 1095-1107.

[4] FENG C, TAGUCHI Y. FasTFit: a fast T-spline fitting algorithm[J]. Computer-Aided Design, 2017, 92: 11-21.

[5] LU Z H, JIANG X, HUO G Y, et al. A fast T-spline fitting method based on efficient region segmentation[J]. Computational and Applied Mathematics, 2020, 39(2): 55.

[6] LAI Y K, HU S M, POTTMANN H. Surface fitting based on a feature sensitive parametrization[J]. Computer-Aided Design, 2006, 38(7): 800-807.

[7] BO P B, LING R T, WANG W P. A revisit to fitting parametric surfaces to point clouds[J]. Computers & Graphics, 2012, 36(5): 534-540.

[8] ECK M, HOPPE H. Automatic reconstruction of B-spline surfaces of arbitrary topological type[C]//The 23rd Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1996: 325-334.

[9] YOSHIHARA H, YOSHII T, SHIBUTANI T, et al. Topologically robust B-spline surface reconstruction from point clouds using level set methods and iterative geometric fitting algorithms[J]. Computer Aided Geometric Design, 2012, 29(7): 422-434.

[10] PIEGL L, TILLER W. The NURBS Book[M]. Berlin, Springer, 1997.

[11] SEDERBERG T W, ZHENG J M, BAKENOV A, et al. T-splines and T-NURCCs[J]. ACM Transactions on Graphics, 2003, 22(3): 477-484.

[12] SEDERBERG T W, CARDON D L, FINNIGAN G T, et al. T-spline simplification and local refinement[J]. ACM Transactions on Graphics, 2004, 23(3): 276-283.

[13] ZHENG J M, WANG Y M, SEAH H S. Adaptive T-spline surface fitting to z-map models[C]//The 3rd International Conference on Computer Graphics and Interactive Techniques in Australasia and South East Asia. New York: ACM Press, 2005: 405-411.

[14] WANG Y M, ZHENG J M. Adaptive T-spline surface approximation of triangular meshes[C]//2007 6th International Conference on Information, Communications & Signal Processing. New York: IEEE Press, 2008: 1-5.

[15] YANG X N, ZHENG J M. Approximate-spline surface skinning[J]. Computer-Aided Design, 2012, 44(12): 1269-1276.

[16] LIN H W, ZHANG Z Y. An efficient method for fitting large data sets using T-splines[J]. SIAM Journal on Scientific Computing, 2013, 35(6): A3052-A3068.

[17] WANG W, ZHANG Y, DU X X, et al. An efficient data structure for calculation of unstructured T-spline surfaces[J]. Visual Computing for Industry, Biomedicine, and Art, 2019, 2(1): 2.

[18] SCOTT M A, SIMPSON R N, EVANS J A, et al. Isogeometric boundary element analysis using unstructured T-splines[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 254: 197-221.

[19] HU X, FU X M, LIU L G. Advanced hierarchical spherical parameterizations[J]. IEEE Transactions on Visualization and Computer Graphics, 2018, 24(6): 1930-1941.

[20] LIU H, YANG Y, LIU Y, et al. Simultaneous interior and boundary optimization of volumetric domain parameterizations for IGA[J]. Computer Aided Geometric Design, 2020, 79: 101853.

[21] YANG Y, FU X M, LIU L G. Computing surface PolyCube-maps by constrained voxelization[J]. Computer Graphics Forum, 2019, 38(7): 299-309.

[22] FU X M, LIU Y, GUO B N. Computing locally injective mappings by advanced MIPS[J]. ACM Transactions on Graphics, 2015, 34(4): 1-12.

Error-bounded unstructured T-spline surface fitting with low distortion

GUAN Qi-chao, LIU Hao, WANG Yuan-cheng, FU Xiao-ming

(School of Mathematical Sciences, University of Science and Technology of China, Hefei Anhui 230000, China)

In order to calculate the unstructured T-spline fitting surface with low distortion and meet the fitting error threshold and fewer control points for any complex topology fitting domain, we presented a step-by-step solution method. First, a polycube structure with the same topology as the fitting domain was generated as the parameter domain, and the corresponding relationship between the surface to be fitted and the parameter domain was optimized through multiple re-parameterization processes, thus obtaining a low distortion mapping suitable for the generation of low fitting error spline surfaces. At the same time, with the local subdivision property of the unstructured T-spline, the region, which did not meet the fitting error threshold, was adaptively subdivided, and the low distortion spline surface meeting the fitting error threshold was obtained. Next, a simplification strategy of fitting surface was presented to delete redundant control vertices. On the basis of meeting the fitting error threshold and low distortion, redundant control vertices were deleted, and a low distortion unstructured T-spline fitting surface was obtained with less control vertices and bounded error. The effectiveness of this method was verified on various complex models. Compared with the latest methods, this method could attain lower parametric distortion with fewer control vertices.

low distortion; unstructured T-spline; surface fitting; polycube structures; local subdivision

TP 391

10.11996/JG.j.2095-302X.2022061104

A

2095-302X(2022)06-1104-10

2022-07-20；

：2022-10-25

国家自然科学基金(61802359)

关启超(1998-)，男，硕士研究生。主要研究方向为计算机辅助几何设计。E-mail：qcguq@mail.ustc.edu.cn

傅孝明(1988-)，男，副教授，博士。主要研究方向为几何处理、计算机辅助几何设计等。E-mail：fuxm@ustc.edu.cn

20 July，2022；

25 October，2022

National Natural Science Foundation of China (61802359)

GUAN Qi-chao (1998-), master student. His main research interest covers computer-aided geometric design. E-mail：qcguq@mail.ustc.edu.cn

FU Xiao-ming (1988-), associate professor, Ph.D. His main research interests cover geometric processing and computer-aided geometric design, etc. E-mail：fuxm@ustc.edu.cn