基于圆堆砌的纹理生成方法
何科雨,陈中贵
基于圆堆砌的纹理生成方法
何科雨,陈中贵
(厦门大学信息学院,福建 厦门 361005)
人造的装饰性纹理在人们的生活中得到了广泛地应用。传统的基于实例的纹理生成方法首先会在目标区域放置一些很小的图元,然后通过迭代的方式让这些图元增长,最后填充整个目标区域。在迭代的过程中相邻的图元之间会发生交叉与覆盖,因此需要对图元做变形、裁剪或其他处理,然而这种处理方式往往会花费大量的时间。基于过程化的方法通过设计很多结构复杂的规则,在二维平面生成具有丰富层次的纹理,但这种方法比较难拓展到三维空间。本文提出了一种基于圆堆砌的纹理生成方法,可以生成二维或三维的纹理。圆堆砌问题属于NP-hard问题,本文将该问题转换成一个最优化问题,从而能够快速近似求解,求解出圆堆砌后就可以在圆上定义规则来对圆形进行填充或替换以生成纹理。由于采用的是设计规则的方式生成纹理,该方法可以避免图元之间发生的交叉覆盖的问题。
圆堆砌;球堆砌;非线性优化;纹理生成;重新网格化
装饰性的纹理是由大量简单的基本图元构成的复杂图案,在人们的日常生活中有广泛地应用,然而由人工手动生成的纹理通常是费时又费力。目前的纹理生成方法主要分为2类:①基于实例的方法,实例是一些简单的几何图元,其可以是图片、几条相交的曲线或多边形等等,通常由用户输入,然后算法将这些实例填充到目标表面,目标表面可以是二维平面或三维网格表面。算法首先会在目标表面进行均匀采样并在采样的位置放置一个比较小的实例,然后采取各种方法让这些实例不断地增长,最后得到一个实例紧密填充的目标表面。在实例增长的过程中相邻的实例可能会发生交叉,因此就需要对相邻实例做适当的变形、裁剪等处理,有时为了让实例填充更紧密又需要对实例进行拉伸处理。然而现有的处理方法都非常费时。②过程化的纹理生成方法,该方法在计算机发展的早期就得到了很多的关注。这种方法通过算法上的设计及少量参数就能够生成带有丰富层次的、复杂的纹理图案,但设计过程的算法并不容易,参数的微小变化会对最终结果产生很大的影响。大多生成的纹理达不到人们的预期,由于生成这种纹理的算法结构复杂,很难有通用的方法将其推广到三维网格表面。本文提出一个基于圆堆砌的纹理生成方法,能够克服上述方法的缺点。圆堆砌指用圆形尽可能对目标区域进行填充,目标区域通常是二维平面中的闭合图形。相邻的圆形不能出现重叠,圆堆砌问题属于NP-hard问题。因此本文采用了启发式的方法,将圆与圆之间的几何约束转换成了数学形式,从而将圆堆砌问题转化成一个最优化问题,并利用最优化库进行快速近似求解,使二维平面上的圆堆砌方法可以很容易拓展到三维网格表面。圆堆砌的最终结果通过三角网格的形式来表示。本文提出了基于圆堆砌生成纹理的方法,即圆堆砌的结果可作为一个框架用于生成纹理,并在圆中放置基本图元,或根据圆与圆之间的几何,拓扑等关系定义各种规则来生成纹理。由于本文的方法不需要处理相邻图元之间的重叠问题,因此具有较高的时间效率。
1 相关工作
本文主要涉及到圆堆砌和纹理生成2个问题,下面将介绍这2方面的相关工作。
1.1 圆堆砌
圆堆砌指用不重叠的圆形对给定的目标区域进行填充,目标区域通常是二维平面上的闭合图形,根据圆的半径是否相等来区分等圆堆砌和不等圆堆砌。SCHIFTNER等[1]通过对三角网格进行优化来得到一个等圆堆砌。本文主要关注不等圆填充,用非线性优化库来求解圆堆砌问题。尽可能对目标区域进行填充,因为本文最终的目标是在圆堆砌的基础上生成纹理,所以对圆的半径和数量没有要求。
1.2 纹理生成
生成纹理的方法主要分为2大类,一类是基于实例的纹理生成方法,另一类是过程化的纹理生成方法。
1.2.1 基于实例的纹理生成方法
基于实例的纹理生成方法通常需要用户提供一个实例,然后通过一系列方法将实例排列到目标区域以获得最终的纹理。实例可以是图片、带有拓扑连接关系的曲线、几何图形等等,根据不同的实例以及不同的目标区域可选择不同的方法。首先是WEI等[2]提出的基于像素图片的方法,输入一张比较小的纹理图片,然后在给定目标区域平面或三维网格表面生成更大范围的纹理,该类方法通常都会用到块匹配[3]算法。块匹配算法能够快速找到图像块之间的对应关系,可以被用来对图像纹理进行拓展。DUMAS等[4]将基于实例的方法拓展到了三维空间且不再局限于对网格表面进行着色,而是生成具有空间结构的镂空网格。其输入是一张二值化的黑白纹理图片,然后将纹理图片紧密排布到三维网格表面,其中黑色的部分最终会生成孔洞,白色的部分会生成网格。ZHOU等[5]用具有网状结构的几何元素替代了二值化的纹理图片,可以生成类似编制物的纹理,并考虑到了相邻几何元素之间的拓扑连接关系而不是相邻图像块之间像素的相似性。
SENDIK和COHEN-OR[6]和ZHOU等[7]通过深度学习的方法学习图片纹理的深度特征,能够将一小块纹理生成更大的纹理,传统的基于块匹配的方法无法生成一些具有全局结构的纹理如树桩,分形图案等。另外一部分文献是基于几何元素排布的,如BARLA等[8]需要用户输入一个矢量化的图案,然后分析图案的结构并进行各个方向上的拓展;IJIRI等[9]采用了类似的方法,通过分析一个给定元素的分布与周围元素的比较来生成新的元素;TU等[10]输入一系列曲线和离散的点,其不仅考虑了元素的位置还考虑了元素与元素之间的拓扑连接;SAPUTRA等[11]在给定目标区域生成了一个流线型向量场,其部分参数可以由用户指定,然后通过对用户输入的实例图元做一些变形来填充到目标空间;HU等[12]通过排布各种形状的闭合多边形到目标空区域,这些多边形可以进行缩放、平移、旋转,但相邻多边形不能出现交叉,其将纹理生成的问题转换成了一个多边形的堆砌问题;CHEN 等[13-14]介绍了生成装饰物纹理的方法,能够自动将一系列图案元素紧密地排列到目标区域,这种纹理生成方法将图案元素的排布转换成了一个关于堆砌的最优化问题,并通过对图案元素进行增长,处理相邻图案重叠的部分以及后续的优化来获得最终的结果。本文参考了文献[13]方法,但是不同的地方在于本文并不直接排布图案元素,而是首先生成一个目标区域的圆堆砌,然后在圆堆砌上生成纹理。ZEHNDER等[15]给用户提供了一个能直接在网格表面操作的曲线网格工具,输入是一些由曲线构成的基本曲线图案,即用户可以自由地在网格表面放置预定义的曲线图案,然后逐渐让这些图案进行增长,不同图案的曲线在增长过程中会出现碰撞,这时图元会发生相应的局部变形,用户也能够在网格模型表面对这些曲线进行编辑;FANNI等[16]采用了体素化的方法,在目标表面采样后放置三角网格实例,然后对这些实例体素化后利用SETHIAN[17]的快速行进算法让实例增长并变形以填充目标表面,该方法最终能够生成与艺术家手工制作出的工艺品类似的结果。
1.2.2 过程化的纹理生成方法
相较于基于实例的方法,过程化的纹理生成方法更加复杂,生成的纹理会有更多的细节,但过程化的方法往往不直观。参数变化会对最终结果产生非常大的影响。EBERT[18]介绍了很多过程化的建模的方法,主要利用各种噪声函数进行不同层次的叠加,通过很少量的代码就能够控制很复杂的纹理细节,该方法能够对树木的纹路、石头纹理、水面、烟雾等自然现象进行模拟。SANTONI和PELLACINI[19]将文法作用于纹理生成,给用户提供了3种不同的操作符用于处理纹理,可以对目标区域做分割,填充不同的图形以及对目标区域进行变形。不同operator的组合作用于目标区域后就能够得到各种不同的纹理图案,该方法只能作用于二维平面,NAZZARO等[20]提出了一个在网格上快速计算测地距离的方法,将文献[19]方法拓展到了三维网格上。LOI等[21]将文法的作用对象进行了拓展,不再局限于对目标区域的划分,纹理中的点线面都可以被视为文法的作用对象。因此能生成结构更加复杂的纹理。文献[19]方法侧重于对目标区域的分割和填充,而文献[21]方法侧重于对具有规律的图案进行程序化的变形和替换。本文对圆形进行替换生成纹理时采用了与文献[21]类似的方法。
GUO等[22]提出了一个能根据图片推测出L系统文法的方法,该首先根据预定义的基本图元和L系统规则生成各种各样的图案,然后训练出一个能够识别图案中基本图元的深度神经网络,最后利用启发式算法推测出原有的L系统文法。WONG等[23]发现很多纹理图案中具有丰富的S型曲线,而这种曲线可以通过相切的圆形得到,于是提出了一个可编程的过程化方法。其能够生成类似植物的装饰性纹,并定义了很多基于圆形的可编程的生长规则,生长规则作用在装饰性元素并根据一系列限制条件决定生成元素的类型及位置。在每次迭代中试探性的选择可能的、最大的位置来放置元素。最终生成一个填满目标区域的纹理图案。
本文主要参考了文献[12-13,23]的方法,首先利用非线性优化快速得到一个目标区域的圆堆砌,然后将圆堆砌的结果作为一个生成纹理的框架。可以构造出S型曲线,也可以放置一些圆形的图元。本文方法既可生成基于实例的纹理,也能够生成过程化的纹理。
2 圆堆砌问题的求解
在介绍生成纹理之前,首先介绍本文对圆堆砌问题的求解过程。圆堆砌问题中有很多约束,本文方法将圆堆砌中的几何约束转换成不等式形式,并设置圆的初始位置及半径,然后利用非线性优化库近似求解出满足约束条件的最大的圆形。
2.1 问题描述
对于二维要在一个给定封闭区域内做圆堆砌,该区域由闭合多边形表示,圆与圆之间不能相交,圆与闭合多边形的边界也不能相交,在满足这些约束的前提下尽可能用圆填充该区域。输入闭合多边形的顶点,输出圆形的半径以及二维坐标。对于三维圆堆砌就变成了球堆砌,所以希望用球尽可能覆盖网格表面,输入是三角网格,输出每一个球的半径以及三维坐标。
2.2 非线性优化求解圆堆砌问题
非线性优化是由一系列约束函数和一个目标函数构成的优化问题。约束函数可以是等式约束也可以是不等式约束,该问题的目标就是求解出满足所有约束函数的目标函数的最大值或最小值。非线性优化问题通常为


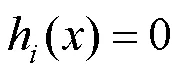
其中,为目标函数;为个最优化参数,目标函数在个参数下取得最大或最小值;fc()为不等式约束,其中=1,···,;h()为等式约束。非线性优化问题是一个比较成熟的问题,目前已经有很多用于求解这类问题的方法,本文采用Knitro[24]优化库来求解,并通过尝试去求解一个局部或全局最优解。在圆堆砌问题中主要有2种类型的约束,一种是圆形与圆形之间的约束,即2个圆之间不能相交;另一种是圆形与边界的约束,即圆与边界也不能相交,圆与圆之间的约束可以看做2个圆心之间的欧氏距离必须大于或等于2个圆形半径之和,圆与边界的约束则是圆心到边线的距离必须大于或等于半径,图1给出约束的具体例子。图1(a)展示了圆-圆约束,红色圆是约束圆,黑色圆是目标圆,数学不等式为

其中,为1指向的单位方向向量;和1和分别为2个圆圆心坐标;与1分别为2个圆半径。
图1(b)展示了圆-边界约束,红色的边为约束边,数学形式为

其中,为指向的单位向量;为过圆心做垂直于边的垂线的垂足。Knitro优化库采用基于梯度的优化方法,因此还需要给出对应约束函数的梯度。本文的问题一共有3个需要优化的参数,分别是点的2个坐标分量以及半径,将约束函数对这3个变量求偏导,即

其中,n,n分别为向量的2个坐标分量。三维情形下的约束与二维情形类似,依然是3个参数,点依然在一个平面进行移动,不同的地方在于从原来在二维平面移动变成了在三维空间中的平面进行移动。首先通过每一个三角网格中的顶点计算出一个切平面,顶点只能够在这个平面上进行移动,二维平面的点需要乘一个矩阵从二维平面变换到切平面上,即

其中,ʹ为变换后的坐标;为切平面上的一个点;为一个3×3的矩阵,其3个行向量分别对应网格顶点所在平面的切向量,副切向量和法向量,即
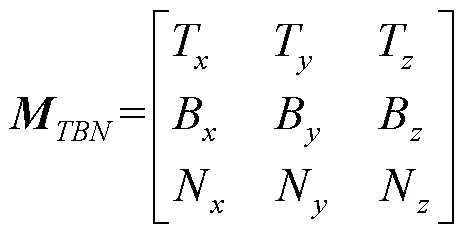
三维情形对应的约束函数的梯度表示为

设置约束后,还需要对优化库设置变量的初始值,即需要设置圆的初始位置以及半径。由于优化库依赖梯度求解,因此不同的初始值最终会收敛于不同的局部最小值,即初始顶点位置的不同对最终算法得到的结果会有很大的影响,如图2所示,其中图2(a)红色矩形与圆为约束,共有4条边与一个圆约束,本文目标是在满足这几个约束的条件下找到一个最大的圆。图2(a)中放置了4个较小的初始圆,图2(b)是利用优化库得到的结果,其中紫色的圆最大,是本文希望得到的结果。可以看出一般情况下优化库只能求解出一个局部最优解,本文采取的策略是从这几个局部最优解中选择最好的结果,即最大的那个圆。

图2 不同初始位置得到的结果((a)初始化;(a)优化结果)
3 基于圆堆砌的纹理生成方法
基于圆堆砌算法的纹理生成方法的核心思想是,基于实例在目标区域放置基本图元,并让这些图元进行增长,然后对相邻图元产生重叠交叉的部分做优化处理。而本文采用的思路是首先对目标区域做圆堆砌以获得一个放置图元的框架,然后在生成的圆内放置基本图元或利用圆与圆之间的关系定义出各种规则并生成不同的纹理图案。这样做就回避了处理相邻图元的阶段。图3(a)为本文算法的总流程图,对于二维平面,输入是闭合多边形,对于三维输入则是三角网格,然后对输入进行重新网格化后执行圆堆砌算法,最后生成纹理,图3(b)为本文圆堆砌算法的流程图。

图3 算法概览((a)算法总流程;(b)圆堆砌流程)
3.1 二维平面的圆堆砌
本文采用三角网格来表示圆堆砌,二维平面的目标表面用闭合多边形来表示且允许存在孔洞。首先利用CGAL库的二维网格优化方法[22-23],根据目标多边形生成一个顶点分布均匀的三角网格={,,},其中是三角形集合,是边集合,是顶点集合,三角网格中的边界以及内部的孔洞都被视为边界边。除边界上的顶点外,三角网格中的每一个顶点都表示一个圆,顶点的坐标就是圆的圆心坐标,每一个顶点都有一个属性来表示圆的半径。圆的初始半径设为0,在计算出三角网格后利用算法2对三角网格中的每一个圆进行优化,本文采用逐顶点迭代优化,对圆进行增长需要设置相应的约束,并选择一环邻域内的顶点及边界边作为约束。如图4所示,当优化顶点为时,顶点约束集合为={1,2,3,4,5,6},边约束集合为={1,2,3,4,5,6},然后利用优化库求解出最大圆的位置以及半径。在优化结束后会存在一些空间未被圆填充,因此需要在这些区域插入圆形来让目标区域获得一个更高的覆盖率。但是本文在具体的实验过程中发现随着插入的圆形半径越来越小,Delaunay三角网格的质量尤其是边界部分网格质量变得非常差,一环邻域约束无法正确的约束圆的位置,导致无法继续插入圆。图5(a)展示了插入圆的结果,对于这个问题本文的解决方案是固定相切边。当一个圆形和一环邻域内的圆形相切或与某一个边界相切时,可定义这条边为相切边,对于与边界相切的圆可在圆与边界相切的部分插入一个新的点以避免形成狭长的三角形。固定这条边后即使以这条边为公共边的2个三角形不满足Delaunay结构也不执行翻边操作。执行这一步后,三角网格不再保持Delaunay三角网格的性质,但是从视觉上更加合理,如图5(b)所示。图5(a)中的三角网格维持Delaunay结构且不处理边界,存在很多穿过圆但不穿过圆心的边,边界网格的质量变得非常差,图5(b)固定了三角网格的部分边,同时对边界做了处理,当某个圆与边界相切时,就在相切的位置插入一个顶点。这样就得到了比图5(a)更加紧凑的结果。图6展示了图5(b)中圆堆砌的生成过程,初始网格为一个矩形,内部有2个三角形,边界边固定,在图中显示为蓝色,图6(b)中放置了第一个圆形,如果不指定的话就会在矩形的正中央生成一个与矩形4条边相切的圆形,图6(c)插入了第一个圆形,新增的这个圆形与矩形的2条边相切,在相切的位置增加了2个顶点并与新增的圆形有一条边相连。
本文通过更进一步的实验发现被固定的相切边和三角网格中原有的边界可以将三角网格分割成多个更小的多边形,小多边形边界全部由相切边或三角网格中原有边界构成,如图7(a)所示,其中蓝色的边为相切边,绿色的边为非相切边。只看相切边,则原来的网格被分割成了2个较小的多边形和一个三角形,由相切边分割出来的多边形相互独立。因此插入圆就可以从原来在整个多边形内插入圆转化成为在多个比较小的多边形内插入圆,并且新插入的圆与原有的圆形会产生新的相切边,新的相切边又能够继续对这些多边形进行分割。本文采用基于三角形的插入策略,对于三角网格中的每一个三角形,首先找到这个三角形所属的多边形的所有圆约束和边界约束,如图7(b)所示,其中边界约束集合={1,2,3,4},顶点约束集合={1,2,3,4},插入圆不同于算法2优化圆的大小,插入圆需要设置一个初始位置,在本文中初始位置一般设置为三角形的重心坐标,如果三角形的重心在某个圆内部,就将坐标做一个偏移移动到该圆的边界上以保证初始位置不会被某个圆形覆盖。然后利用优化库求解出基于当前三角形的最大圆,并将这个圆定义为候选圆。如果一开始插入比较小的圆形,后面插入的圆就只会越来越小,这将不利于后面的纹理生成,为了避免最后插入的圆太小,所以希望每一次都能插入一个比较大的圆。因此需对每一个三角形都计算出一个候选圆,然后选择最大的候选圆插入。新插入的圆会与原有的圆相切,形成新的相切边,这些边需要被固定,由于插入圆是在当前三角形所属的多边形内部进行的,并不会对外部的多边形产生任何影响。因此每一次插入圆都是一个局部优化问题,并不需要再次重新计算每一个三角形的候选圆,只需要对闭合多边形内部的三角形进行重新计算。
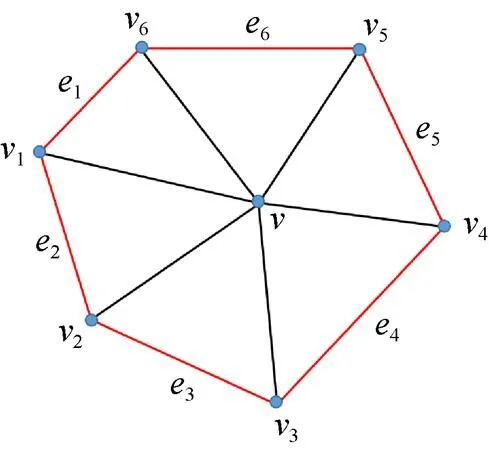
图4 三角网格约束示例

图5 不固定边与固定边的结果对比((a)不固定边;(b)固定边))

图6 初始网格以及插入部分圆形的过程((a)初始网格;(b)放置一个初始的圆;(c)插入一个圆;(d)插入2个圆;(e)插入3个圆形;(f)最终结果)
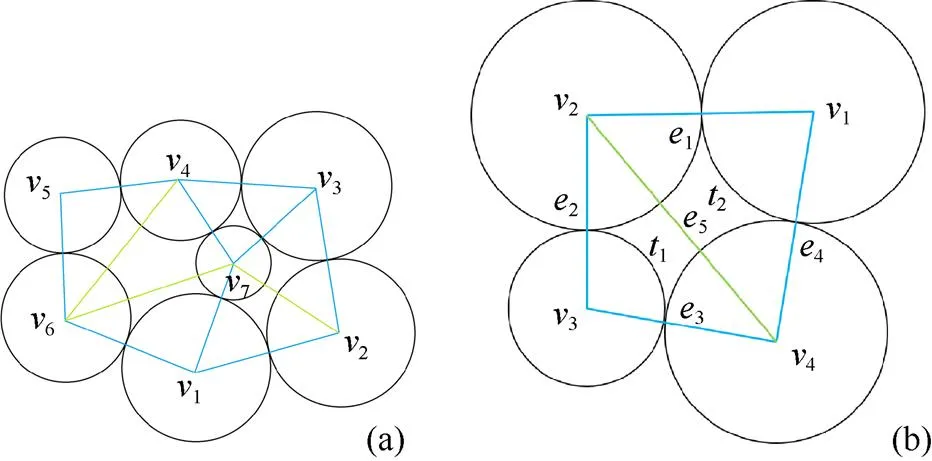
图7 分割多边形示例((a)多边形分割;(b)最小多边形约束)
算法1.圆堆砌算法。
输入:平面区域(由闭合多边形表示Ω),半径阈值。
输出:三角网格。
步骤1.在闭合多边形上生成顶点均匀分布的Delaunay三角网格;
步骤2.用算法2对每一个圆进行优化;
步骤3.固定边界;
步骤4.对于三角网格中的每一个三角形利用算法3计算出最大圆位置以及半径并插入最大的一个圆,当找到的最大圆半径小于阈值时结束。
算法2.圆优化算法。
输入:三角网格和需要被优化的圆形对应的顶点。
输出:优化后的圆坐标和半径。
步骤1.找到顶点的一环邻域的顶点以及一环邻域边界边;
步骤2.将和写成约束形式;
步骤3.利用优化库求解出优化后圆形的半径以及坐标;
步骤4.翻边以维持Delaunay结构。
算法3.插入圆算法。
输入:三角网格和的三角形。
输出:优化后的圆坐标和半径。
步骤1.找到三角形所属的最小闭合多边形的边界集合以及顶点集合;
步骤2.将和写成约束形式;
步骤3.设置初始位置;
步骤4.根据约束利用优化库求解出最大圆;
步骤5.固定新的相切边。
在实际求解圆堆砌的过程中,目标区域的边界约束中往往存在内部凹陷或孔洞结构,如图8(a)所示,考虑到本文的边界约束,凹多边形中边界约束会压缩实际的可行空间。图中目标区域是一个闭合的凹多边形,一共有6个边界约束,其中3,4这2条边内凹。在本文提出的边界约束下整个目标区域实际上会被划分成3个更小的区域,如图8(c)所示,在这种情况下只能生成3个较小的圆,不能有效利用多边形的空间。本文的解决方法为,首先将边界约束边按照逆时针方向排列,如图8(d)所示,箭头表示该边,然后依次计算每一条边的方向向量结果,如果方向向量由屏幕外指向屏幕内,则这2条边属于凹边,对于凹边的约束只需约束圆心的位置,即只保证圆心的位置不会穿过这个边界约束,如图8(b)所示,数学形式为
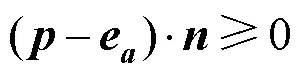
同时增加一个点约束,点约束可以看作半径为0的圆约束,其圆心位于2条凹边的交点,即图8(e)中3,4这2条边的交点1。通过设置约束后,就能够在有凹结构的目标区域中求解出最大的圆,即图8(e)中黑色的圆。
图8 凹多边形的处理((a)凹边界约束;(b)不约束半径的边界约束;(c)不处理凹结构;(d)找出凹结构;(e)处理凹结构)
Fig. 8 Processing of concave polygons ((a) Concave boundary constraints; (b) Boundary constraints without radius constraints; (c) Without handling concave structures; (d) Finding concave structures; (e) Dealing with concave structures)
图9展示了包含孔洞的闭合多边形的圆堆砌过程。其中图9(a)为初始网格,由2个闭合多边形构成,内部的闭合多边形为孔洞,图9(b)为将初始网格重新网格化后的结果,利用算法2对图9(b)网格中的每一个非边界顶点进行优化后就得到了图9(c),图9(d)展示了在空白部分插入圆(红色)后得到的结果,图9(e)展示了部分凹结构的细节。
3.2 三维网格表面的球堆砌
球堆砌是对二维平面的圆堆砌的拓展,相较于二维的圆与圆的约束与圆与边界约束,到了三维空间就变成了球与球的约束和球与边界的约束,算法与二维平面的圆堆砌基本一致,在算法2圆优化这一步需要为三角网格中每一个球计算一个切平面,将球心的坐标限制在这个切面内进行优化。一个平面可以通过一个法向量和一个三维空间中过平面的坐标确定,坐标即球心的坐标,法向量由该球对应网格顶点一环邻域内部三角形所在平面的法向量取平均值得到。算法3采用基于三角形的插入圆策略,被插入的圆只能限制在三角形所在平面内进行移动。图10给出了球堆砌的例子,首先输入一个三角网格,然后对这个网格进行重新网格化让顶点均匀分布,使球堆砌的结果中球的分布较均匀,然后执行球堆砌算法。图10(b)和(c)展示了球堆砌的结果。

图9 带有孔洞的圆堆砌结果((a)初始网格;(b)重新网格化;(c)初始圆堆砌;(d)插入圆后的圆堆砌;(e)凹结构细节)

图10 三维网格球堆砌上的几何纹理生成((a)输入网格;(b)重新网格化;(c)球堆砌;(d)生成纹理)
3.3 二维平面的纹理生成
在得到二维圆堆砌的结果后,就可按上述定义规则来生成纹理,本文主要参考了文献[21,23]的方法,如图11所示。在圆堆砌上生成纹理的规则如下,首先定义由2个圆构成的圆对,圆对中的一个圆必须是另一个圆一环邻域中的圆,且一个圆只能出现在一个圆对中。用贪心策略找到圆堆砌中的所有圆对,然后开始绘制,首先将所有的圆按一定比例缩小后绘制边框,并在2个圆之间绘制一条线段,线的方向由2个圆的圆心坐标决定,长度为2个圆的圆心距离减去其半径。

图11 二维纹理生成示例((a)圆堆砌结果;(b)纹理生成)
3.4 三维网格表面的纹理生成
三维网格表面的纹理生成与二维情形类似,图10(d)展示了三维网格模型球堆砌后生成的纹理,之前已计算出了每一个球对应三角网格中顶点的法向量,然后利用法向量和球生成圆环模型,其中圆环的朝向由法向量确定,圆环的半径与圆心位置与球的半径和球心位置一致。
4 结果与比较
4.1 二维圆堆砌纹理
本文方法能够处理具有不规则形状的图形,图12展示了几个不规则形状的圆堆砌结果,可以看出本文的方法对于不规则图形具有鲁棒性。图13展示了本文二维圆堆砌纹理的结果,其中图13(a)和(b)的纹理图案在图12(a)和(b)圆堆砌的基础上得到,该图案由3种基本的图元组成,红色的问号,黄色的感叹号以及绿色的句号,本文利用这3种图元来替代图12(a)中圆堆砌中的圆。
首先本文采用用贪心算法找到圆堆砌中所有的圆对,圆对中2个圆形大小相当的圆形会被问号图元替代,大小差距较大的圆对则会被感叹号替代,剩下的没有被匹配到圆对中的圆形则会被用句号来替代。图13(b)采用了另一种方法生成纹理,对于每一个圆,在以其圆周为轴,半径长度为轴的非欧坐标系中叠加不同频率的正弦波就能够得到不同的图案。图13(c)采用了图片纹理来替换圆形,绿色的荷叶图案与粉色的莲花图案,在进行替换的过程为了让生成的结果更加具有真实感,对每一个圆的位置做了一个比较小的偏移,最终生成的纹理产生重叠的效果,图13(d)采用了另外一种思路,对三角网格中的三角形进行替代,生成了类似花瓣的纹理。

图12 不规则多边形内的圆堆砌((a) C字形;(b) I字形;(c)不规则形状)
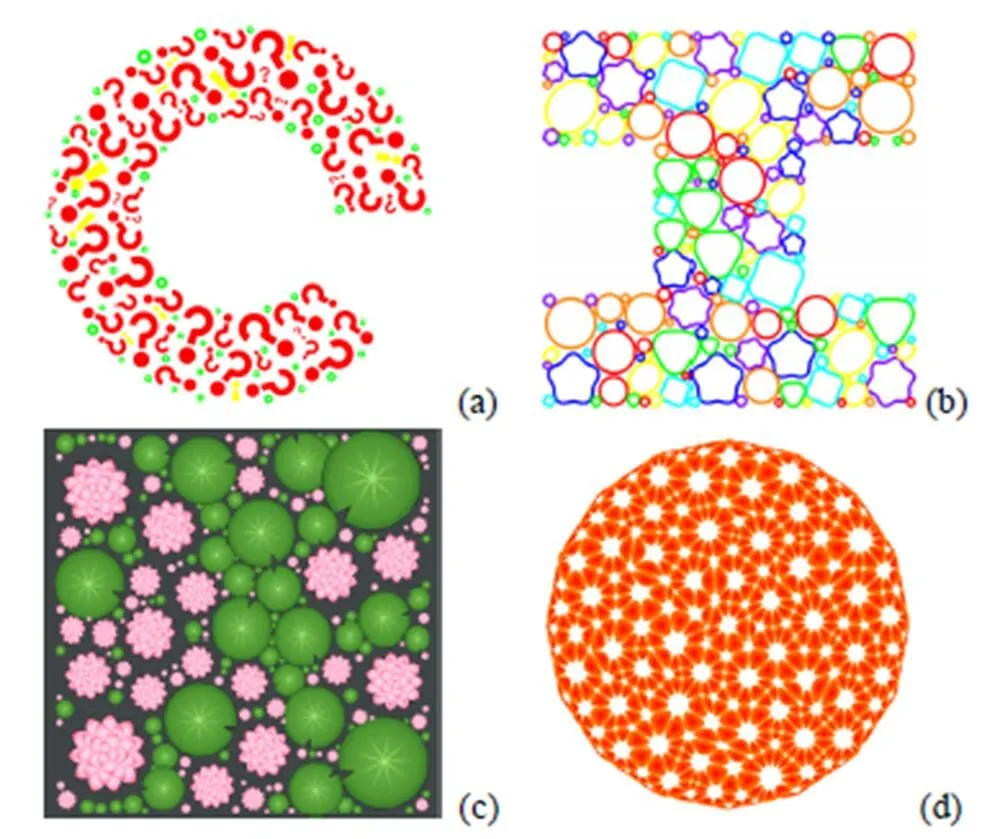
图13 二维圆堆砌上的纹理生成((a)符号纹理;(b)星号纹理;(c)池塘纹理;(d)花朵纹理)
4.2 三维网格球堆砌纹理
图14展示了本文三维网格球堆砌的结果,图14(a)与图14(b)均采用了鸡蛋形状的网格模型用于球堆砌,图14(c)采用了圆环作为基础网格。此外,本文对部分生成的纹理做了平滑处理,图14(d)所采用的具有S形状以及螺旋形状的纹理是定义在圆上的,因此将纹理放在三维球的切平面上,而在三维空间中相邻球的切平面往往是不相交,2个相邻的球的连接处只有一个切点,因此本文采用样条线的方式来进行连接,从而得到一个平滑的过渡效果,从图14的结果中可以看出,本文,方法在光滑的网格表面有比较好的表现。

图14 三维网格上球堆砌导出的纹理((a)鸡蛋1;(b)水管;(c)圆环;(d)鸡蛋2)
4.3 方法比较
图15和图16展示了本文和文献[19]在二维纹理上的比较,图15展示了字母图案填充纹理,本文方法能够得到类似的结果,能够获得一个更加稠密的填充。图15中字母a和c中的方形元素是对圆形替换后的结果,方形元素的对角线长度等于圆形的半径。图16展示了本文与文献[19]方法在狮子图案上生成的纹理,文献[19]设计出了对各种图案都通用的operator,其包括对图案的分割、填充以及扭曲变形,通过对这些不同的operator进行各种组合就可以生成很多不同的纹理图案。本文首先对图案进行圆堆砌,然后对圆进行分组并用不同的规则生成的图案替代原有的圆形。从图中可以看出,本文能够很好地保持图案中的一些尖锐特征,虽然采用了不同的方法,本文也能够得到令人满意的结果。

图15 二维纹理结果对比((a)文献[19]中的字母图案填充;(b)本文的字母图案填充)

图16 二维狮子图案纹理((a)文献[19]中的狮子纹理;(b)本文的狮子纹理)
图17展示了本文与文献[13]方法的对比,用于生成纹理的基础网格模型是一个球形,最终生成的是一个有镂空结构的花纹球体。可以从图17(a)中看出,球面的花纹全部由单一的图元进行拼接得到。为了获得一个稠密的结果,文献[13]算法需要进行大量的迭代来对相邻图元进行变形、裁剪。而本文方法是在考虑了相邻球之间的连接关系后直接在球上生成纹理图案,不需要对图元做任何变形操作,因此在得到近似结果的前提下,本文方法在运行时间上有比较大的优势。

图17 三维纹理结果对比((a)文献[13]中的球形纹理;(b)本文的球形纹理;(c)文献[13]中的兔子纹理;(d)本文的兔子纹理)
4.4 运行时间
本文方法绝大部分时间用于计算圆堆砌和球堆砌,表1和表2给出了本文所有案例圆堆砌与球堆砌的运行时间以及对应的三角网格的顶点数量。本文所使用的电脑配置为Intel i7-7000 CPU,8GB RAM。文献[13]方法在图17(a)和图17(c)中的纹理分别用时1 428 s,816 s。而本文的方法在图17(b)和图17(d)分别用时4.74 s和61.189 s。

表1 圆堆砌运行时间及三角网格顶点数量

表2 球堆砌运行时间及三角网格顶点
5 结束语
本文提出的基于圆堆砌的纹理生成方法简单、鲁棒、速度快,能够处理二维凹多边形,具有较强的实用性,同时对于光滑的三维网格模型也能得到比较好的结果。但本文方法也有一定的局限性,不能很好地保持三维网格模型的尖锐特征,如图17(d)中兔子的耳朵部分,在生成纹理的种类上也存在较大的限制。圆堆砌问题是一个很经典的问题,在很多领域都有广泛地应用,本文主要将圆堆砌用于纹理生成,对于圆堆砌在其他领域的应用未来将展开更多研究。
[1] SCHIFTNER A, HÖBINGER M, WALLNER J, et al. Packing circles and spheres on surfaces[C]//ACM SIGGRAPH Asia 2009 Papers on - SIGGRAPH Asia '09. New York: ACM Press, 2009: 1-8.
[2] WEI L Y, LEFEBVRE S, KWATRA V, et al. State of the art in example-based texture synthesis[C]//Eurographics 2009, State of the Art Report, EG-STAR. Eindhoven: Eurographics Association, 2009: 93-117.
[3] BARNES C, SHECHTMAN E, GOLDMAN D B, et al. The generalized PatchMatch correspondence algorithm[C]// Computer vision - ECCV 2010. Berlin: Springer, 2010: 29-43.
[4] DUMAS J, LU A, LEFEBVRE S, et al. By-example synthesis of structurally sound patterns[J]. ACM Transactions on Graphics, 2015, 34(4): 137.
[5] ZHOU K, HUANG X, WANG X, et al. Mesh quilting for geometric texture synthesis[C]//SIGGRAPH '06: ACM SIGGRAPH 2006 Papers. New York: ACM Press, 2006: 690-697.
[6] SENDIK O, COHEN-OR D. Deep correlations for texture synthesis[J]. ACM Transactions on Graphics, 2017, 36(5): 161.
[7] ZHOU Y, ZHU Z, BAI X, et al. Non-stationary texture synthesis by adversarial expansion[EB/OL]. [2022-05-20]. https://arxiv.org/abs/1805.04487.
[8] BARLA P, BRESLAV S, THOLLOT J, et al. Stroke pattern analysis and synthesis[J]. Computer Graphics Forum, 2006, 25(3): 663-671.
[9] IJIRI T, MÊCH R, IGARASHI T, et al. An example-based procedural system for element arrangement[J]. Computer Graphics Forum, 2008, 27(2): 429-436.
[10] TU P H, WEI L Y, YATANI K, et al. Continuous curve textures[J]. ACM Transactions on Graphics, 2020, 39(6): 168.
[11] SAPUTRA R A, KAPLAN C S, ASENTE P, et al. FLOWPAK: flow-based ornamental element packing[C]//The 43rd Graphics Interface Conference. New York: ACM Press, 2017: 8-15.
[12] HU W C, CHEN Z G, PAN H, et al. Surface mosaic synthesis with irregular tiles[J]. IEEE Transactions on Visualization and Computer Graphics, 2016, 22(3): 1302-1313.
[13] CHEN W K, ZHANG X L, XIN S Q, et al. Synthesis of filigrees for digital fabrication[J]. ACM Transactions on Graphics, 2016, 35(4): 98.
[14] CHEN W K, MA Y X, LEFEBVRE S, et al. Fabricable tile decors[J]. ACM Transactions on Graphics, 2017, 36(6): 175.
[15] ZEHNDER J, COROS S, THOMASZEWSKI B. Designing structurally-sound ornamental curve networks[J]. ACM Transactions on Graphics, 2016, 35(4): 99.
[16] FANNI F A, PELLACINI F, SCATENI R, et al. PAVEL: decorative patterns with packed volumetric elements[EB/OL]. [2022-06-17]. https://arxiv.org/abs/2102.01029.
[17] SETHIAN J A. Fast marching methods[J]. SIAM Review, 1999, 41(2): 199-235.
[18] EBERT D S. Texturing & modeling: a procedural approach[M]. 3rd ed. Amsterdam: Morgan Kaufmann Publishers, 2003.
[19] SANTONI C, PELLACINI F. gTangle: a grammar for the procedural generation of tangle patterns[J]. ACM Transactions on Graphics, 2016, 35(6): 182.
[20] NAZZARO G, PUPPO E, PELLACINI F. geoTangle: interactive design of geodesic tangle patterns on surfaces[J]. ACM Transactions on Graphics, 2022, 41(2): 12.
[21] LOI H, HURTUT T, VERGNE R, et al. Programmable 2D arrangements for element texture design[J]. ACM Transactions on Graphics, 2017, 36(3): 27.
[22] GUO J W, JIANG H Y, BENES B, et al. Inverse procedural modeling of branching structures by inferring L-systems[J]. ACM Transactions on Graphics, 2020, 39(5): 155.
[23] WONG M T, ZONGKER D E, SALESIN D H. Computer- generated floral ornament[C]//The 25th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1998: 423-434.
[24] BYRD R H, NOCEDAL J, WALTZ R A. Knitro: an integrated package for nonlinear optimization[M]//Nonconvex Optimization and Its Applications. Boston: Springer, 2006: 35-59.
Circle packing based texture generation
HE Ke-yu, CHEN Zhong-gui
(School of Informatics, Xiamen University, Xiamen Fujian 361005, China)
Artificial decorative textures are in wide use in our lives. The traditional case-based texture generation methods would first place some small primitives on the target area, then iteratively grow these primitives, and finally fill the entire target area. In the iteration process, there would be intersections and overlays between adjacent primitives, entailing the deforming, clipping, and other processing of primitives, which was usually time-consuming. Procedure-based methods can generate textures with rich layers in the two-dimensional plane by designing various rules with complex structures. However, such methods would be difficult to extend to the 3D space. This paper provided a texture generation method based on circle packing, thereby generating 2D or 3D textures. As an NP-hard problem, the circle packing problem could be converted into a nonlinear optimization problem, so that it could be quickly and approximately solved. With the problem solved, different rules could be defined to fill or replace the circle to generate textures. Since the texture is generated by rules, the proposed method could avoid intersections and overlays between primitives.
circle packing; sphere packing; non-linear optimization; texture generation; remeshing
TP 391
10.11996/JG.j.2095-302X.2022061114
A
2095-302X(2022)06-1114-10
2022-07-31;
:2022-10-25
国家自然科学基金(61972327);福建省自然科学基金资助项目(2022J01001)
何科雨(1998-),男,硕士研究生。主要研究方向为计算机图形学。E-mail:1205486810@qq.com
陈中贵(1982-),男,教授,博士。主要研究方向为计算机图形学、几何造型与处理、计算机辅助设计等。E-mail:chenzhonggui@xmu.edu.cn
31 July,2022;
25 October,2022
National Natural Science Foundation of China (61972327); Natural Science Foundation of Fujian Province (2022J01001)
HE Ke-yu (1998-), master student. His main research interest covers computer graphics. E-mail:1205486810@qq.com
CHEN Zhong-gui (1982-), professor, Ph.D. His main research interests cover computer graphics, geometric modeling and processing, computer-aided design, etc. E-mail:chenzhonggui@xmu.edu.cn

