图形图像积分与微分不变量的构造与应用

墨瀚林，郝 优，郭 锐，郝宏翔，张 贺，李 琪，李 华

图形图像积分与微分不变量的构造与应用

墨瀚林1,2，郝 优1,2，郭 锐1,2，郝宏翔1,2，张 贺1,2，李 琪1,2，李 华1,2

(1. 中国科学院计算技术研究所智能信息处理重点实验室，北京 100190；2. 中国科学院大学计算机科学与技术学院，北京 100049)

作为图形图像数据的常用特征，微分不变量和以矩不变量为代表的积分不变量在计算机视觉、模式识别和计算机图形学等领域扮演了重要角色。在过去二十年中，本研究团队利用基本生成函数构造了灰度图像、彩色图像、向量场、点云、曲线和网格曲面等图形图像数据在几何变换、颜色变换、图像模糊和全变换下的矩不变量；证明了仿射变换下几何矩不变量与微分不变量之间满足同构关系，提出了一种获取仿射微分不变量的简单方法，并进一步得到了射影变换和莫比乌斯变换下图形图像的微分不变量；为了增强深度神经网络对常见图形图像变换的不变性，探索了如何将图形图像不变量引入深度神经网络模型。系统回顾与总结了上述工作，简要介绍了如何使用基本生成函数构造图形图像在仿射变换下的几何矩不变量与微分不变量，分析了图形图像不变量的典型应用场景及优缺点，并对未来的研究进行了展望。

图形图像变换；特征提取；矩不变量；微分不变量；图像分类；形状分析；模板匹配

1 简 介

如何提取图形图像数据的有效特征始终是计算机视觉、模式识别和计算机图形学等领域的核心问题。理想的图形图像特征应当对常见变换具有不变性。事实上，受传感器参数、设备架设角度、外界光照变化等因素的影响，针对同一目标采集的不同数据间往往满足某种变换关系。如，使用相机从不同角度拍摄同一平面物体，所得到的图像之间满足二维射影变换关系，如图1所示。显然，对各类外加变换具有鲁棒性或不变性是图形图像特征能够准确描述目标内在信息的必要条件。

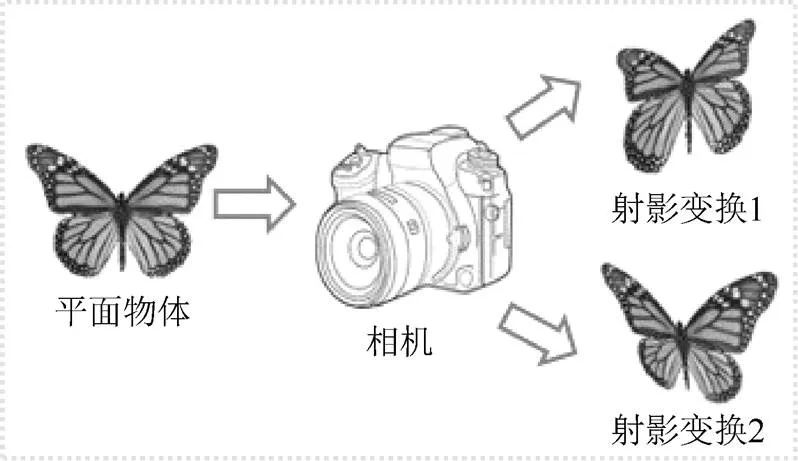
图1 二维射影变换导致的几何形变

半个世纪以来，各种变换下的图形图像不变特征层出不穷，其中，积分不变量与微分不变量扮演了重要的角色。以矩不变量(moment invariants)为代表的积分不变量常被用来提取图形图像数据的整体信息。1962年，HU[1]首次将几何中心矩的概念引入图像分析领域，并使用经典的代数不变量理论得到了7个对二维相似变换具有不变性的几何矩不变量。此后，利用图方法[2]、几何基元法[3]等生成方法，该领域的研究者相继得到了灰度图像、彩色图像、向量场、三维点云、曲线和网格曲面等数据在几何变换[4-8]、光照变换[9-13]、图像模糊[14-18]等多种常见图形图像变换下的几何矩不变量。为了提升矩不变量对噪声的鲁棒性，部分研究者使用不同类型的正交多项式定义了图形图像的正交矩并生成了上述变换下的正交矩不变量[19-23]。目前，矩不变量已经被广泛应用于形状分析[24-26]、物体识别[27-29]、医学影像分析[30-32]和语音分析[33-34]等众多任务中。如，文献[31]通过提取大脑磁共振图像的几何矩不变量来检测阿尔兹海默症等脑部疾病；文献[33]则使用基于局部几何矩不变量的加权谱特征来分析语音数据的情感。相对于矩不变量，微分不变量(differential invariants)更适合被用来描述图形图像的局部结构。目前，研究者主要使用OLVER[35-36]提出的移动标架等价方法生成常见图形图像变换下的微分不变量。利用旋转微分不变量，KOENDERINK和VAN DOORN[37]定义了形状指数特征(shape index)和弯曲度特征(curvedness)，并用于描述曲面的局部结构；文献[38-41]发现部分旋转和仿射变换下的微分不变量能够被用来检测图像中的特定局部结构(如“团”结构或角点)并能确定该结构的空间尺度；GRIFFIN等[42-43]利用旋转微分不变量描述图像局部区域的对称性，并进一步定义了纹理图像的基本图像特征(basic image features，BIF)。

可以看出，积分与微分不变量适用于多种图形图像变换且应用场景广泛，同时，两者具有较强的互补性。在过去二十年中，本研究团队对图形图像积分与微分不变量进行了较为系统的研究，并取得了一系列成果，具体包括：

(1) 使用基本生成函数，提出了相似和仿射变换下一般标量函数矩不变量的生成框架[44-45]，以及全变换(total transform)下一般向量函数矩不变量的生成框架[46-47]。使用上述框架，得到了图形图像数据在多种几何变换[6-7, 48]、颜色变换[10-13]以及图像模糊[17-18]下的矩不变量实例。

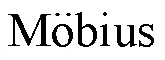
(3)初步探索了图形图像积分与微分不变量和目前流行的卷积神经网络(convolution neural network，CNN)的结合方式[52]，设计了在图像旋转变换下具有不变性的梯度对齐卷积操作[53]。

上述不变量和提升CNN模型不变性的方法已经被应用于图形图像的检索与分类[3,54]、人体骨架识别[55]、模板匹配[17]、向量场分析[47]等任务中。

本文对上述工作进行了总结与回顾，并对图形图像不变量未来的研究进行了展望；同时，为加深读者的理解，以仿射变换为例，简单介绍如何使用基本生成函数构造图形图像在该变换下的矩不变量实例，并给出了与其满足同构关系的微分不变量。

2 基本概念与定义

2.1 常见的图形图像变换

目前，文献中常见的图像变换可以被分为4类，即二维几何形变、光照变化、图像模糊以及多类型变换的复合(如形状-颜色双仿射变换)，而针对图形变换的讨论则大多只涉及三维几何形变。如，对任意二维平面物体，可以使用二维平移、旋转、缩放、相似、仿射和射影变换模型来描述其由相机拍摄角度变化导致的几何形变，不同变换模型之间满足图2所示的集合关系。以仿射变换为例，假设二维坐标点(,)T和(,)T之间满足仿射变换关系，则有

其中，2×2非奇异矩阵2为二维仿射变换；2×1向量2为二维平移，即

其中，矩阵2和向量2中的参数均为实数。若将图2中的变换模型推广到三维，则能够使用其描述三维图形变换。如，2个三维坐标点(,,)T和(,,)T之间的仿射变换关系可以被表示为

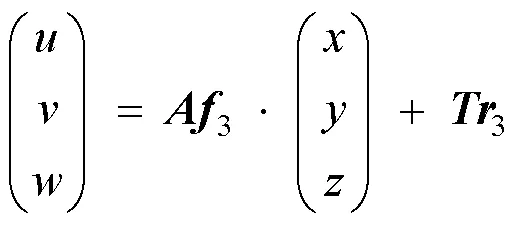
其中，3为3×3非奇异矩阵；3为3×1平移向量。事实上，使用双视角图像对某个三维目标进行重建时，其不同仿射重建版本的对应坐标点之间即满足式(3)所定义的关系。

图2 平面物体的常用几何变换模型

Fig. 2 Commonly used transform models for planar objects

2.2 图形图像矩不变量

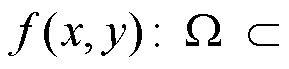
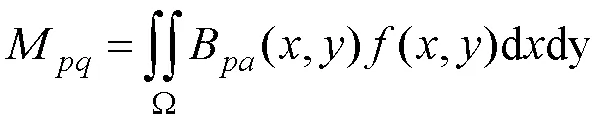
其中，B为任意类型的多项式基底；和为非负整数，(+)被称为图像矩的阶数。简言之，可以将图像矩理解为整幅图像在某类多项式基底上的投影。目前，最常用的图像矩是基于幂函数基底{x y}构造的图像几何中心矩，即

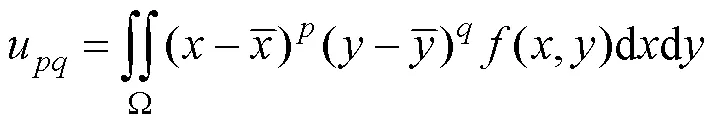
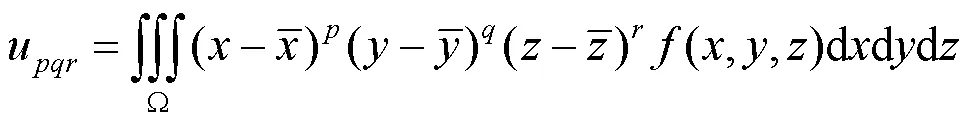
矩不变量是矩的一类特殊函数，其通常对某种图形图像变换具有不变性。目前常见的图形图像矩不变量大多可以被表示为矩的齐次多项式形式。如，基于几何中心矩构造的图像几何矩不变量为

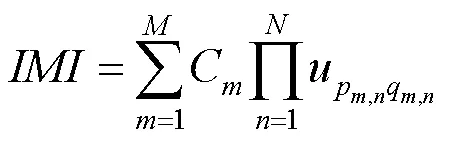
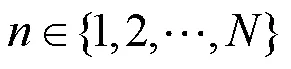
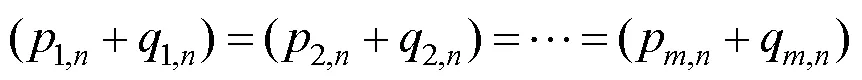
2.3 图形图像微分不变量

微分不变量是另一类重要的图形图像不变量。事实上，由泰勒展开式可知，若函数在某点无穷阶可导，则其在该点邻域内的全部信息可以由其无穷阶偏微分完整提取，这正是使用图形图像函数的各阶偏微分数值描述其局部结构的理论基础。然而，偏微分对大部分图形图像变换并不具有不变性，在实际应用中往往表现不佳。如，图像梯度(即图像函数(,)的一阶偏微分)会随着二维旋转变换而改变。因此，在计算以尺度不变特征变换(scale-invariant feature transform，SIFT)[56]为代表的图像梯度描述子时，需要先估计图像的主方向，将其变换到标准位置后再计算梯度。

为此，研究人员开始使用微分不变量描述图形图像的局部结构。类似于矩与矩不变量的关系，微分不变量是各阶偏微分的函数，通常对某种特定变换具有不变性。理论上，可以被表示为偏微分的任意函数，如多项式函数、有理多项式函数等。但是，FLORACK等[57-58]已经证明，任意非多项式形式的微分不变量均可被表示为具有齐次多项式形式的微分不变量的函数。因此，相比于其他形式的微分不变量，具有齐次多项式形式的微分不变量更加本质，因而成为研究重点。如，可以将图像(,)的微分不变量表示为

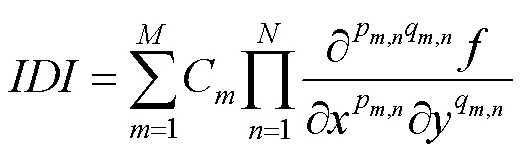
其中，各参数的定义与式(7)相同，且满足式(8)定义的关系。

3 仿射变换下矩不变量的生成函数

本节重点介绍仿射变换下图形图像几何矩不变量的基本生成函数。令图像(,)的定义域为，坐标点(x,y)T和(x,y)T属于，T为质心坐标，则其基本生成函数为

其中，

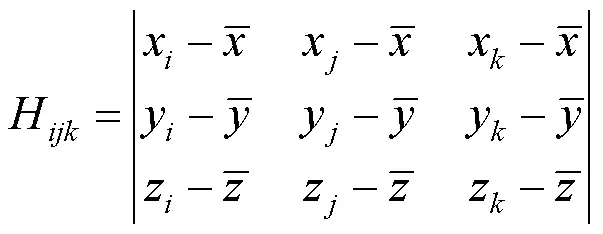
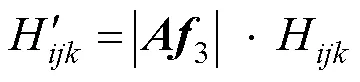
其中，

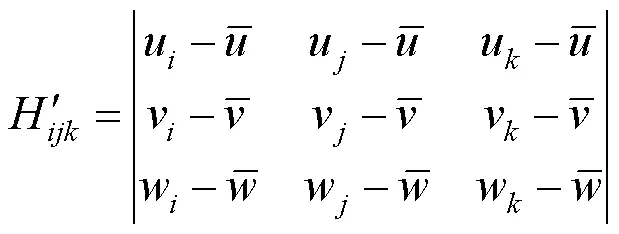
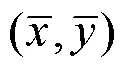
4 仿射变换下矩不变量的构造

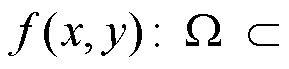
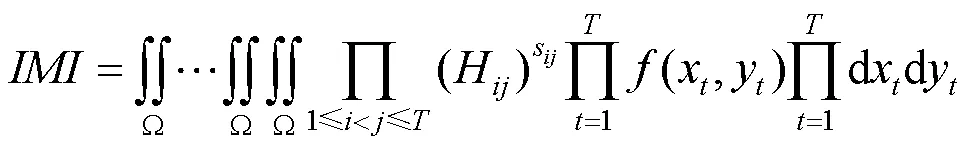
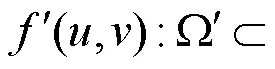
图3 二维和三维行列式的几何意义((a)二维行列式Hij；(b)三维行列式Hijk)

Fig. 3 The geometric meanings of 2D and 3D determinants((a)2D determinant Hij; (b)3D determinant Hijk)

其中，

其中，(·)为绝对值函数，生成函数的定义由式(12)给出。文献[45]利用式(11)和积分换元法证明了式(17)，并说明了的展开式是式(7)定义的图像几何中心矩齐次多项式。因此，使用式(16)构造的在二维仿射变换前后只相差一个与变换矩阵的行列式相关的常数。事实上，先前的研究[2-4]已经表明，该常数可以使用不同方法消除，如多个的比值。

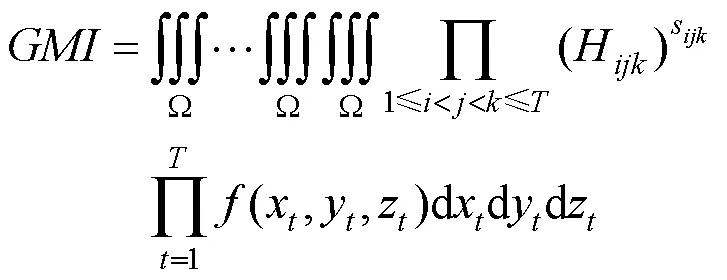
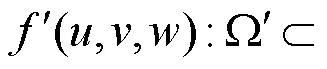
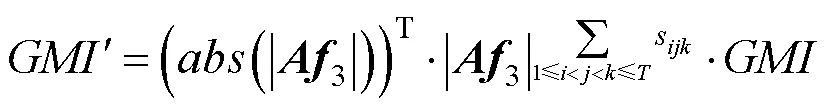
其中，

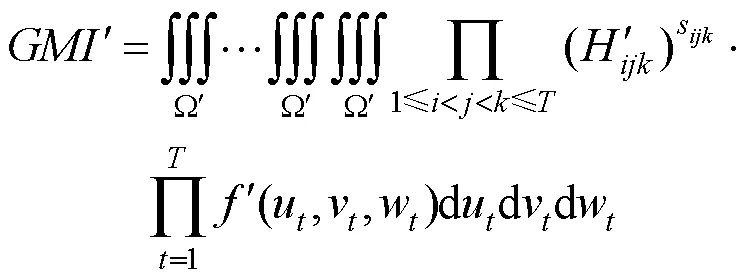
最近，DIAO等[59]进一步证明了基本生成函数H和H是构造仿射变换下图形图像几何矩不变量的充分必要条件。为了更加清楚地说明如何使用式(16)和式(19)生成仿射矩不变量，式(22)和式(23)分别给出=2和=3时2个简单和实例的构造过程。对照式(7)和式(8)，可以看出式(22)生成的图像不变量实例确实为图像几何中心矩的齐次多项式。例如，在式(22)中，参数==1=2，2=–2，同时几何矩阶数满足(1,1+1,1)=(2,1+2,1)= (2,1+2,1)=(2,2+2,2)=2。

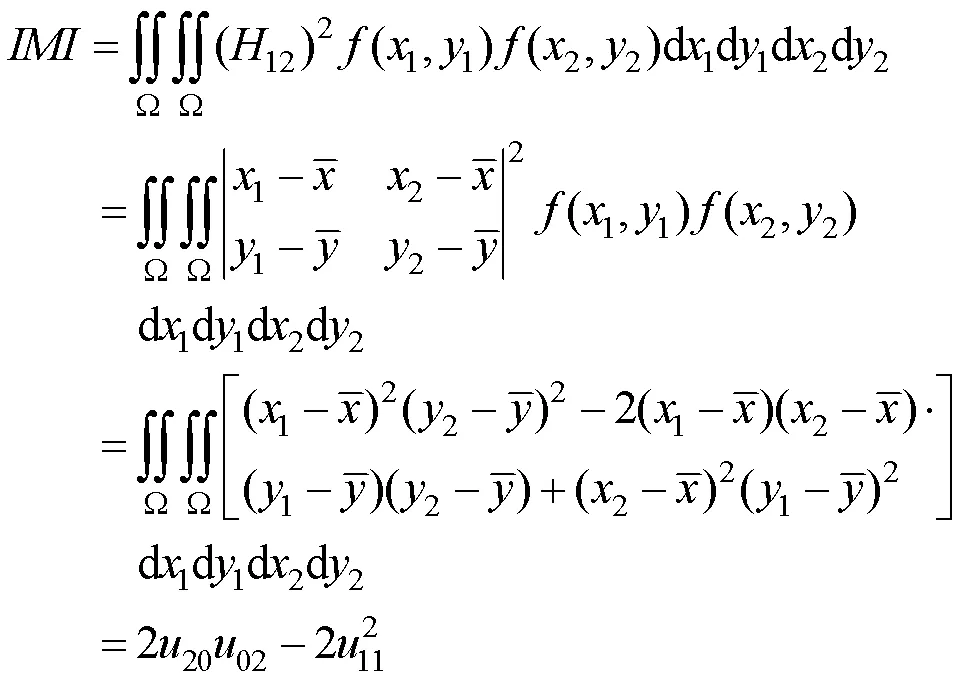
5 仿射变换下微分不变量的生成

如前所述，先前的研究[35-36, 57-58]大多使用移动标架等价方法生成图形图像的仿射微分不变量。最近，本研究团队证明在仿射变换下几何矩不变量与微分不变量之间具有同构关系[49]，该发现大大简化了获取仿射微分不变量的难度。具体而言，给定任意仿射矩不变量，只需将其中的几何中心矩替换为同阶偏微分即可得到对应的仿射微分不变量。

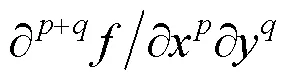
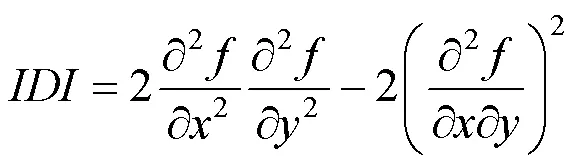
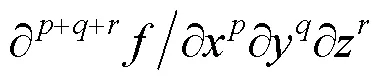
6 其他变换下的积分与微分不变量

除仿射变换外，本研究团队已经得到不同图形图像数据在下列变换下的积分和微分不变量。

6.1 图像射影变换

如图1所示，二维射影变换能够表示平面物体因拍摄视角变化导致的任意形变。事实上，当相机与平面物体间的距离远大于物体自身尺寸时，射影变换的射影性较弱。此时，仿射变换能够较好的近似射影变换。然而，当该条件不被满足时，基于仿射不变量构建的图像检索或分类算法性能明显下降。因此，构造图像在射影变换下的积分或微分不变量是有意义的。

如图2所示，仿射变换是射影变换的子集，因此射影微分不变量也是仿射微分不变量。假如能够得到足够多的仿射微分不变量实例，则可能从中筛选出射影微分不变量。利用第5节仿射微分不变量与矩不变量间的同构关系，文献[50, 60]系统生成了图像仿射微分不变量，并从中发现了2个图像射影微分不变量；随后，首次证明了射影变换下图像矩不变量的存在，这种矩不变量能够被表示为图像微分加权矩的齐次多项式，其中，先前得到的图像射影微分不变量被作为加权函数；最后，给出了一组简单的图像射影加权矩不变量实例，并详细分析了实际计算过程中可能的误差来源。

6.2 反射变换

反射变换是另一类常见的图形图像几何变换，具体而言，变换前后的2个物体互为镜像。如图4显示了满足反射变换关系的一对灰度图像和一对人体网格数据。手性与非手性是一组与反射变换具有紧密联系的物体属性。若对于任意反射变换，物体均与其镜像不同，则称其具有手性；若物体存在对称轴或对称平面，则沿其对称轴或对称平面进行反射变换后得到的镜像与该物体完全相同，如二维空间中的圆和三维空间中的立方体等，这种性质被称为非手性。显然，图4(a)的灰度图像具有手性，而图4(b)的三维人体网格则近似具有非手性。

图4 图形图像数据的反射变换((a)灰度图像的反射变换；(b)三维人体网格的反射变换)

实际生活中存在大量满足对称性的非手性物体，构造反射变换下的图形图像不变量对于分析其结构具有重要意义。基于第3节的基本生成函数，文献[48, 61]给出了反射变换下图形图像几何矩不变量的构造方式，并给出了5个简单的不变量实例。图5显示了使用该组不变量进行三维人脸对称性检测得到的结果。如图5(a)所示，该三维人脸网格模型为非手性物体，以轴所在的平面为对称面，网格上各点处的颜色表示某个反射矩不变量在以该点为中心的局部区域上计算得到的数值。显然，反射几何矩不变量的数值分布关于平面对称，即在2个满足反射变换关系的位置上计算得到的不变量数值互为相反数。基于此，将5个反射几何矩不变量的数值作为网格上每个顶点的特征，在选定一个顶点后，可基于特征距离判断其镜像 对称点，进而计算出人脸模型的对称平面，如 图5(b)所示。

图5 三维人脸对称面检测((a)反射几何矩不变量数值分布；(b)人脸对称平面检测结果)

6.3 莫比乌斯变换

莫比乌斯变换是平移、缩放、旋转、反射和反演变换的组合，其中，反演变换(inversion transform)使其区别于等距变换。图6给出了满足反演变换关系的一对灰度图像和一对人体网格数据。相较于仿射、射影变换这类全局变换，莫比乌斯变换只保证物体的局部形状在变换前后满足某种性质，因此能够描述更加复杂和真实的图形图像形变。事实上，莫比乌斯变换与共形变换(conformal transform)有着密切的联系。GEHRIM[62]证明了三维及三维以上空间的共形变换与莫比乌斯变换等价。最近，计算共形几何的相关理论与技术被成功应用于医学图像分析、形状分析和几何分类等任务中，并取得了良好的效果[63-65]。事实上，共形变换正是共形几何研究的基础和重要组成部分。因此，构造图形图像在莫比乌斯变换下的不变量不仅有助于更深入的理解共形变换，而且能够进一步提升当前算法在形状分析等任务上的表现。

在先前的研究中，最常用的莫比乌斯不变量为交叉比。文献[51, 61]首次得到了图形图像函数在反演变换下的微分不变量实例，其中包括拉普拉斯算子与梯度内积的比值；随后，验证了其对平移、旋转、缩放和反射变换同样具有不变性，进而确认了其是莫比乌斯变换下的微分不变量。

图6 图形图像数据的反演变换((a)灰度图像的反演变换；(b)三维人体网格的反演变换)

6.4 图像模糊

图像模糊是一类常见的图像变换，包括失焦模糊、直线运动模糊、旋转运动模糊和径向运动模糊等。如，图7(a)和(b)分别显示了灰度图像的旋转运动模糊和失焦模糊版本。

图7 不同类型图像模糊((a)旋转运动模糊；(b)失焦模糊)

文献[66-67]首次提出了旋转运动模糊下图像几何矩不变量的生成方法；随后，文献[18]基于该方法得到了图像在该变换下的Gaussian-Hermite正交矩不变量，相对于前者，后者具有更强的噪声鲁棒性。先前的研究发现，满足重旋转对称性的点扩散函数与原图像进行卷积能够较好的模拟由镜头失焦导致的真实图像模糊。文献[17]建立了一种获得几何形变和旋转对称模糊下图像几何矩不变量的直观方法。具体而言，对任意满足重旋转对称性的点扩散函数，首先证明了其同阶几何中心矩之间存在线性依赖关系。基于该性质，提出了一种判断现存图像相似或仿射几何矩不变量是否同时对重旋转对称模糊具有不变性的简单方法。与先前的相关工作不同，该方法并不依赖复杂的操作或构造公式。使用该方法，分析了最经典的图像矩特征—HU矩[1]，发现其中的5个不变量对重对称模糊具有天然的不变性，并首次得到了仿射变换和重对称模糊下的矩不变量实例。

6.5 向量函数的全变换

伴随着数据仿真和采集技术的不断发展，多通道数据的获取变得越来越容易。在计算机视觉和图形学领域，常见的多通道数据包括彩色图像、二维向量场和三维流场等，其均可以被看作是一般向量函数的不同实例。值得注意的是，前文介绍的旋转、相似和仿射变换等作用于空间坐标域的几何变换模型并不具备描述向量函数真实形变的能力，因为这些形变往往同时出现在坐标域和向量域。为此，研究者提出了全变换的概念，具体包括全旋转变换(total rotation transform)、旋转-仿射变换(rotation-affine transform)和全仿射变换(total affine transform)等。如，旋转-仿射变换能够同时建模拍摄视角变化和外界光照变换导致的彩色图像几何旋转变换和颜色仿射变换，图8(a)显示了一幅彩色图像的旋转-仿射变换版本；同样的，如图8(b)所示，研究者们通常使用全旋转变换对向量场数据的局部形变进行建模。

图8 不同类型向量函数的全变换((a)彩色图像的旋转-仿射变换；(b)二维向量场的全旋转变换)

利用本文第3节介绍的仿射变换下矩不变量的基本生成函数，文献[11]首先构造了彩色图像在形状-颜色双仿射变换下的几何矩不变量。事实上，该变换是一般全仿射变换在彩色图像数据上的特例。基于该方法，文献[46, 68]进一步提出了全仿射变换下一般向量函数几何矩不变量的构造框架。最近，文献[13]提出了旋转-仿射变换下彩色图像Gaussian-Hermite正交矩的构造方法，文献[47]则将该方法推广到了一般向量函数。如前文所述，相对于几何矩不变量，全变换下的正交矩不变量对噪声具有更强的鲁棒性。

6.6 不变量的应用场景与优缺点

积分与微分不变量是一类具有一般性的特征，可应用于图形图像领域的不同任务中。如，文献[3, 44]将三维几何矩不变量用于图形检索；文献[50, 60]将图像射影不变量实例应用于图像检索、纹理分类等任务，证明了其在二维射影变换下比目前常用的图像矩不变量具有更好的稳定性和区分性；基于TOSCA数据集中的三维人脸网格模型，文献[51, 61]验证了莫比乌斯微分不变量在网格点匹配任务中的性能；文献[17]发现HU矩在模糊图像分类、检索和模板匹配任务中具有良好的稳定性和区分性，并指出该经典特征在众多任务中均表现良好的原因之一是其具有较强的模糊不变性；文献[47]则将全变换下向量函数的矩不变量应用于彩色图像分类、向量场涡旋检测等任务中。

相比其他类型的图形图像特征，积分与微分不变量具有如下2个显著的优点。首先，不变量适用于多种数据类型和多种图形图像变换。通过上述介绍本文已经得到了灰度图像、彩色图像、向量场、点云、曲线和网格曲面等图形图像数据在几何变换、颜色变换、图像模糊和全变换下的矩不变量。其次，不变量具有较强的可解释性。且文献[38-41]已经发现了部分使用一、二阶偏微分构造的旋转和仿射微分不变量具有明确的几何意义，其数值对某些图像局部结构具有特殊的响应。

作为一种基础特征，积分与微分不变量善于提取图形图像数据的形状、纹理和颜色等基本信息，却并不能够被直接用来提取数据的高级语义信息，这导致不能完全满足某些实际应用的需求。如，在一般图像分类任务中，属于同一类别的图像(即包含同类目标)往往是在不同场景下拍摄的，几何和颜色变换无法描述其之间满足的关系。显然，若在整幅图像上计算积分不变量，则其数值可能出现较大变化，进而导致分类器无法基于该特征准确预测图像的类别。另外，已有研究表明，使用高阶矩或偏微分构造的不变量具有计算复杂度高、数值稳定性差等缺点，而低阶不变量的数目又非常有限，这限制了图形图像不变量特征最终的维数。

7 不变量与深度神经网络的结合

2012年以来，以卷积神经网络(convolutional neural network，CNN)为代表的深度神经网络在计算机视觉和图形学的诸多任务中取得了巨大成功。事实上，通过在大规模数据集上进行训练，深度神经网络能够有效地提取图形图像数据的高级语义特征。然而，先已有研究表明，传统CNN模型本身并不具备常见图形图像变换下的不变性。如，传统卷积操作只对平移变换具有不变性，以旋转变换为例，如果在训练阶段不使用数据增广方法，即使输入的图形图像数据只发生了微小的旋转变换，CNN模型的性能也会骤降[69-70]。这使得越来越多的研究者开始思考如何提升常见图形图像变换下CNN模型的不变性。

显然，图形图像不变量与深度神经网络具有互补性，若能将前者的变换不变性与后者的高级语义特征提取能力相结合，将进一步提升CNN模型在图形图像领域各类任务上的性能。为此，文献[52]使用本文第4节介绍的方法构造图像仿射矩不变量IMI，并将其引入了CNN网络中，如图9所示。具体而言，首先在各卷积层输出的特征图上计算IMI，然后将其与最后一层卷积层的输出串联并一起输入全连接层，用来指导网络参数的学习。实验结果表明，该方法明显提升了CNN对图像仿射变换的鲁棒性。值得注意的是，这种结构适用于任意类型的不变量，以提升CNN模型对特定变换的不变性。部分研究者通过修改标准卷积操作来提升CNN的不变性。事实上，对某种变换具有不变性的卷积操作具备提取该变换下图形图像不变特征的能力。最近，文献[53]提出了梯度对齐卷积，使用其替换CNN中的标准卷积可以实现模型对图像旋转变换的不变性。由于旋转不变性被固化在网络结构中，不需要使用数据增广方法对修改后的CNN模型进行训练。相比于其他同类方法，该网络结构在具有旋转特性的MNIST-rotation和Plankton-sub-rotation等数据集上取得了最优结果。

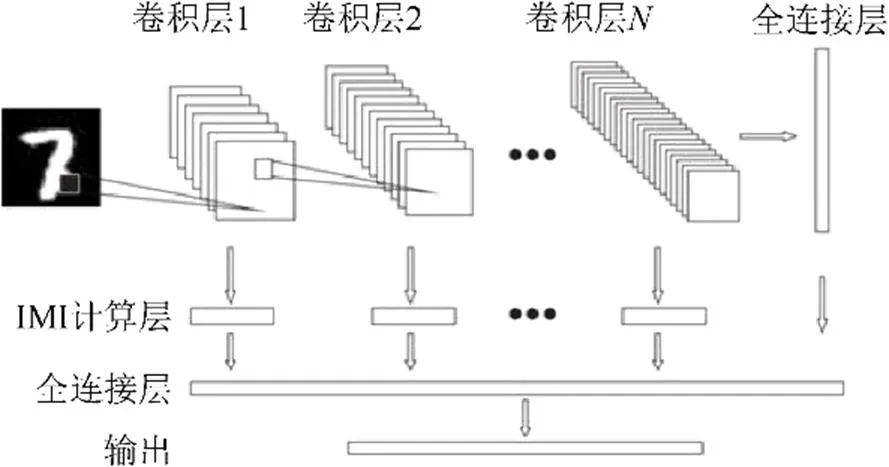
图9 图像仿射不变量网络结构

8 总结与展望

在过去二十年中，本研究团队对图形图像积分与微分不变量进行了较为系统的研究，得到了大量常见变换下图形图像矩不变量和微分不变量的实例，并测试了其在实际任务中的性能，本文对相关工作进行了总结和回顾，重点介绍了如何使用简单的基本生成函数构造仿射变换下图形图像的矩不变量，并利用矩不变量与微分不变量的同构关系获得仿射微分不变量；简要回顾了射影变换、反射变换、莫比乌斯变换、图像模糊和向量函数全变换下图形图像矩不变量或微分不变量的生成与应用；为了提升深度神经网络模型在常见图形图像变换下的不变性，说明了如何将图形图像不变量引入CNN模型，并设计了对图像旋转变换具有不变性的梯度对齐卷积操作。

未来的研究将主要聚焦于以下3个方面：定义复杂变换模型更好的模拟真实的图形图像形变，构造新变换下的矩不变量与微分不变量；分析高阶积分与微分不变量的几何含义，为其赋予明确的语义信息；通过分析不变量与深度神经网络的优势与劣势，将不变量或其他不变特征构造过程中获取不变性的手段和方法引入深度神经网络结构中，进一步增强网络对于常见变换的不变性，从而提升其在分类或检索任务中的准确率。

[1] HU M K. Visual pattern recognition by moment invariants[J]. IRE Transactions on Information Theory, 1962, 8(2): 179-187.

[2] SUK T, FLUSSER J. Affine moment invariants generated by graph method[J]. Pattern Recognition, 2011, 44(9): 2047-2056.

[3] XU D, LI H. Geometric moment invariants[J]. Pattern Recognition, 2008, 41(1): 240-249.

[4] FLUSSER J, SUK T. Affine moment invariants: a new tool for character recognition[J]. Pattern Recognition Letters, 1994, 15(4): 433-436.

[5] SUK T, FLUSSER J. Affine moment invariants of color images[M]//Computer analysis of images and patterns. Berlin: Springer, 2009: 334-341.

[6] XU D, LI H. 3-D affine moment invariants generated by geometric primitives[C]//The 18th International Conference on Pattern Recognition. New York: IEEE Press, 2006: 544-547.

[7] XU D, LI H. 3-D surface moment invariants[C]//The 18th International Conference on Pattern Recognition. New York: IEEE Press, 2006: 173-176.

[8] SCHLEMMER M, HERINGER M, MORR F, et al. Moment invariants for the analysis of 2D flow fields[J]. IEEE Transactions on Visualization and Computer Graphics, 2007, 13(6): 1743-1750.

[9] MINDRU F, TUYTELAARS T, GOOL L V, et al. Moment invariants for recognition under changing viewpoint and illumination[J]. Computer Vision and Image Understanding, 2004, 94(1-3): 3-27.

[10] GONG M, LI H, CAO W G. Moment invariants to affine transformation of colours[J]. Pattern Recognition Letters, 2013, 34(11): 1240-1251.

[11] GONG M, HAO Y, MO H L, et al. Naturally combined shape-color moment invariants under affine transformations[J]. Computer Vision and Image Understanding, 2017, 162: 46-56.

[12] MO H L, LI S R, HAO Y, et al. Shape-color differential moment invariants under affine transforms[M]//Communications in computer and information science. Singapore: Springer Singapore, 2017: 183-196.

[13] 墨瀚林, 郝优, 李华. 形状和颜色变换下图像的Gaussian-Hermite矩不变量[J]. 计算机辅助设计与图形学学报, 2022, 34(3): 341-351.

MO H L, HAO Y, LI H. Gaussian-Hermite moment invariants of image to shape and color transforms[J]. Journal of Computer-Aided Design & Computer Graphics, 2022, 34(3): 341-351 (in Chinese).

[14] FLUSSER J, SUK T, SAIC S. Recognition of blurred images by the method of moments[J]. IEEE Transactions on Image Processing: A Publication of the IEEE Signal Processing Society, 1996, 5(3): 533-538.

[15] FLUSSER J, ZITOVÁ B. Combined invariants to linear filtering and rotation[J]. International Journal of Pattern Recognition and Artificial Intelligence, 1999, 13(8): 1123-1135.

[16] FLUSSER J, SUK T, BOLDYS J, et al. Projection operators and moment invariants to image blurring[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(4): 786-802.

[17] MO H L, HAO H X, LI H. Geometric moment invariants to spatial transform and-fold symmetric blur[J]. Pattern Recognition, 2021, 115: 107887.

[18] 郭锐, 贾丽, 郝宏翔, 等. 基于Gaussian-Hermite矩的旋转运动模糊不变量[J]. 中国图象图形学报, 2022, 27(8): 2458-2472.

GUO R, JIA L, HAO H X, et al. Rotational motion blur invariants based on Gaussian-Hermite moments[J]. Journal of Image and Graphics, 2022, 27(8): 2458-2472 (in Chinese).

[19] TEAGUE M R. Image analysis via the general theory of moments[J]. JOSA, 1980, 70(8): 920-930.

[20] SHENG Y, ARSENAULT H H. Experiments on pattern recognition using invariant Fourier-Mellin descriptors[J]. Journal of the Optical Society of America A, Optics and Image Science, 1986, 3(6): 771-776.

[21] BELKASIM S O, SHRIDHAR M, AHMADI M. Pattern recognition with moment invariants: a comparative study and new results[J]. Pattern Recognition, 1991, 24(12): 1117-1138.

[22] YANG B, SUK T, FLUSSER J, et al. Rotation invariants from Gaussian-Hermite moments of color images[J]. Signal Processing, 2018, 143: 282-291.

[23] HOSNY K M, DARWISH M M. New set of multi-channel orthogonal moments for color image representation and recognition[J]. Pattern Recognition, 2019, 88: 153-173.

[24] ŽUNIĆ J, HIROTA K, ROSIN P L. A Hu moment invariant as a shape circularity measure[J]. Pattern Recognition, 2010, 43(1): 47-57.

[25] ŽUNIĆ D, ŽUNIĆ J. Shape ellipticity from hu moment invariants[J]. Applied Mathematics and Computation, 2014, 226: 406-414.

[26] ŽUNIĆ J, ROSIN P L, ILIĆ V. Disconnectedness: a new moment invariant for multi-component shapes[J]. Pattern Recognition, 2018, 78: 91-102.

[27] DU J X, WANG X F, ZHANG G J. Leaf shape based plant species recognition[J]. Applied Mathematics and Computation, 2007, 185(2): 883-893.

[28] MA X J, PAN R L, WANG L. License plate character recognition based on Gaussian-Hermite moments[C]//The 2nd International Workshop on Education Technology and Computer Science. New York: IEEE Press, 2010: 11-14.

[29] ZHAO J D, WANG X K. Vehicle-logo recognition based on modified HU invariant moments and SVM[J]. Multimedia Tools and Applications, 2019, 78(1): 75-97.

[30] BENTOUTOU Y, TALEB N, CHIKR EL MEZOUAR M, et al. An invariant approach for image registration in digital subtraction angiography[J]. Pattern Recognition, 2002, 35(12): 2853-2865.

[31] ZHANG Y D, WANG S H, SUN P, et al. Pathological brain detection based on wavelet entropy and Hu moment invariants[J]. Bio-Medical Materials and Engineering, 2015, 26(s1): S1283-S1290.

[32] ZHANG Y D, ZHANG Y, LV Y D, et al. Alcoholism detection by medical robots based on Hu moment invariants and predator-prey adaptive-inertia chaotic particle swarm optimization[J]. Computers & Electrical Engineering, 2017, 63: 126-138.

[33] SUN Y X, WEN G H, WANG J B. Weighted spectral features based on local Hu moments for speech emotion recognition[J]. Biomedical Signal Processing and Control, 2015, 18: 80-90.

[34] MONGE-ÁLVAREZ J, HOYOS-BARCELÓ C, LESSO P, et al. Robust detection of audio-cough events using local hu moments[J]. IEEE Journal of Biomedical and Health Informatics, 2019, 23(1): 184-196.

[35] OLVER P J. Equivalence, invariants, and symmetry[M]. Cambridge: Cambridge University Press, 1995: 136-164.

[36] OLVER P J. Classical invariant theory[M]. Cambridge: Cambridge University Press, 1999: 62-85.

[37] KOENDERINK J J, VAN DOORN A J. Surface shape and curvature scales[J]. Image and Vision Computing, 1992, 10(8): 557-564.

[38] LINDEBERG T. Scale selection for differential operators[M]//Scale-space theory in computer vision. Boston: Springer US, 1994: 317-348.

[39] LINDEBERG T, GÅRDING J. Shape-adapted smoothing in estimation of 3-D shape cues from affine deformations of local 2-D brightness structure[J]. Image and Vision Computing, 1997, 15(6): 415-434.

[40] MIKOLAJCZYK K, SCHMID C. Scale & affine invariant interest point detectors[J].International Journal of Computer Vision, 2004, 60(1): 63-86.

[41] MIKOLAJCZYK K, TUYTELAARS T, SCHMID C, et al. A comparison of affine region detectors[J]. International Journal of Computer Vision, 2005, 65(1): 43-72.

[42] GRIFFIN L D, LILLHOLM M. Symmetry sensitivities of derivative-of-Gaussian filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(6): 1072-1083.

[43] GRIFFIN L D, LILLHOLM M, CROSIER M, et al. Basic image features (BIFs) arising from approximate symmetry type[M]//Lecture notes in computer science. Berlin: Springer, 2009: 343-355.

[44] 徐东. 三维几何矩不变量研究及其应用[D]. 北京: 中国科学院计算技术研究所, 2008.

XU D. Research and application of three-dimensional geometric moment invariants[D]. Beijing: Institute of Computing Technology, Chinese Academy of Sciences, 2008 (in Chinese).

[45] LI E B, HUANG Y Z, XU D, et al. Shape DNA: basic generating functions for geometric moment invariants[EB/OL]. (2019-11-19) [2022-05-30]. https://arxiv.org/abs/1703.02242.

[46] HAO Y, MO H L, LI Q, et al. Dual affine moment invariants[EB/OL]. (2019-11-19) [2022-05-30]. https://arxiv.org/abs/1911.08233.

[47] MO H L, LI H, ZHAO G Y. Gaussian-Hermite moment invariants of general vector functions to rotation-affine transform[EB/OL]. (2022-01-03) [2022-05-30]. https://arxiv.org/abs/2201.00877.

[48] ZHANG H, MO H L, HAO Y, et al. Fast and efficient calculations of structural invariants of chirality[J]. Pattern Recognition Letters, 2019, 128: 270-277.

[49] LI E B, LI H. Isomorphism between differential and moment invariants under affine transform[EB/OL]. (2017-05-24) [2022-05-30]. https://arxiv.org/abs/1705.08264.

[50] LI E B, MO H L, XU D, et al. Image projective invariants[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(5): 1144-1157.

[51] ZHANG H, MO H L, HAO Y, et al. Differential and integral invariants under Mu00f6bius transformation[M]//Pattern recognition and computer vision. Cham: Springer International Publishing, 2018: 280-291.

[52] HAO Y, LI Q, MO H L, et al. AMI-net: convolution neural networks with affine moment invariants[J]. IEEE Signal Processing Letters, 2018, 25(7): 1064-1068.

[53] HAO Y, HU P, LI S R, et al. Gradient-Aligned convolution neural network[J]. Pattern Recognition, 2022, 122: 108354.

[54] HAO Y, LI S R, MO H L, et al. Affine-gradient based local binary pattern descriptor for texture classification[M]//Lecture notes in computer science. Cham: Springer International Publishing, 2017: 199-210.

[55] 李琪, 墨瀚林, 赵婧涵, 等. 时空双仿射微分不变量及骨架动作识别[J]. 中国图象图形学报, 2021, 26(12): 2879-2891.

LI Q, MO H L, ZHAO J H, et al. Spatio-temporal dual affine differential invariants for skeleton-based action recognition[J]. Journal of Image and Graphics, 2021, 26(12): 2879-2891 (in Chinese).

[56] LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110.

[57] FLORACK L M J, TER HAAR ROMENY B M, KOENDERINK J J, et al. Scale and the differential structure of images[J]. Image and Vision Computing, 1992, 10(6): 376-388.

[58] FLORACK L M J, ROMENY B M T H, KOENDERINK J J, et al. Cartesian differential invariants in scale-space[J]. Journal of Mathematical Imaging and Vision, 1993, 3(4): 327-348.

[59] DIAO L H, ZHANG Z M, LIU Y J, et al. Necessary condition of affine moment invariants[J]. Journal of Mathematical Imaging and Vision, 2019, 61(5): 602-606.

[60] 墨瀚林. 基于不变量的图像结构分析与应用[D]. 北京: 中国科学院大学, 2021.

MO H L. Analysis and application of image structure based on invariant[D]. Beijing: University of Chinese Academy of Sciences, 2021 (in Chinese).

[61] 张贺. 基于共形不变特征的形状分析与识别[D]. 北京: 中国科学院大学, 2019.

ZHANG H. Shape analysis and identification based on invariants under conformal transformation[D]. Beijing: University of Chinese Academy of Sciences, 2019 (in Chinese).

[62] GEHRIM F W. Topics in quasiconformal mappings[M]//Lecture notes in mathematics. Berlin: Springer, 1992: 30-38.

[63] GU X, YAU S T. Surface classification using conformal structures[C]//The 9th IEEE International Conference on Computer Vision. New York: IEEE Press, 2008: 701-708.

[64] GU X F, WANG Y L, CHAN T F, et al. Genus zero surface conformal mapping and its application to brain surface mapping[J]. IEEE Transactions on Medical Imaging, 2004, 23(8): 949-958.

[65] WANG S, WANG Y, JIN M, et al. Conformal geometry and its applications on 3D shape matching, recognition, and stitching[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(7): 1209-1220.

[66] HAO. H X, MO. H L, LI H. Geometric moment invariants to motion blur[EB/OL]. (2021-01-25) [2022-05-30]. https://arxiv.org/abs/2101.08647.

[67] 郝宏翔. 图像运动模糊矩不变量的研究与应用[D]. 北京: 中国科学院大学, 2021.

HAO H X. Research and application of image motion blur moment invariants[D]. Beijing: University of Chinese Academy of Sciences, 2021 (in Chinese).

[68] 郝优. 仿射不变性分析与应用[D]. 北京: 中国科学院大学, 2020.

HAO Y. Affine invariance analysis and application[D]. Beijing: University of Chinese Academy of Sciences, 2020 (in Chinese).

[69] JADERBERG M, SIMONYAN K, ZISSERMAN A, et al. Spatial transformer networks[C]//International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2015: 2017-2025.

[70] BAWEJA H S, PARHAR T. Leprosy lesion recognition using convolutional neural networks[C]//2016 International Conference on Machine Learning and Cybernetics. New York: IEEE Press, 2017: 141-145.

The construction and application of integral invariants and differential invariants of graphics and images

MO Han-lin1,2, HAO You1,2, GUO Rui1,2, HAO Hong-xiang1,2, ZHANG He1,2, LI Qi1,2, LI Hua1,2

(1. Key Laboratory of Intelligent Information Processing, Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100190, China; 2. School of Computer Science and Technology, University of Chinese Academy of Sciences, Beijing 100049, China)

As common features for graphics and images, differential invariants and integral invariants represented by moment invariants play significant roles in such fields as computer vision, pattern recognition, and computer graphics. In the past two decades, based on fundamental generating functions, our research group have constructed moment invariants of various data types of graphics and images, including grayscale images, color images, vector fields, point clouds, curves, and mesh surfaces, under the conditions of geometric transforms, color transforms, image blurring, and total transforms. The research proved the existence of the isomorphism between geometric moment invariants and differential invariants under affine transform, proposed a simple method for the generation of affine differential invariants by means of this property, and further derived differential invariants of graphics and images under projective transform and Möbius transform. In order to enhance the invariance of deep neural networks for the commonly used graphic/image transform models, the exploration was conducted on how to combine certain invariants of graphics or images with deep neural network models. This paper reviewed and summarized our previous work. In addition, a brief introduction was presented on how to utilize fundamental generating functions to generate geometric moment invariants and differential invariants of graphics and images under affine transform. Analyses were also undertaken on typical applications, advantages, and disadvantages of graphic and image invariants, with future research plan proposed.

transforms of graphics and images; feature extraction; moment invariants; differential invariants; image classification; shape analysis; template matching

TP 391

10.11996/JG.j.2095-302X.2022061182

A

2095-302X(2022)06-1182-11

2022-07-31；

：2022-11-06

国家重点研发计划项目(2017YFB1002700)；国家自然科学基金项目(61379082)

墨瀚林(1992-)，男，博士研究生。主要研究方向为计算机视觉与模式识别。E-mail：mohanlin@ict.ac.cn

李 华(1957-)，男，研究员，博士。主要研究方向为计算机图形学。E-mail：lihua@ict.ac.cn

31 July，2022；

6 November，2022

National Key R&D Program of China (2017YFB1002700); National Natural Science Foundation of China (61379082)

MO Han-lin (1992-), Ph.D. candidate. His main research interests cover computer vision and pattern recognition. E-mail：mohanlin@ict.ac.cn

LI Hua (1957-), professor, Ph.D. His main research interest covers computer graphics. E-mail：lihua@ict.ac.cn