社会网络环境下融合概率语言和QUALIFLEX的绿色包装评价方法
周 欢 张培颖 刘 嘉
1. 湖南工业大学商学院 湖南 株洲 412007
2. 湖南工业大学 湖南省包装经济研究基地 湖南 株洲 412007
0 引言
随着我国生态文明建设及“双碳”战略的持续推进,人们在购买商品时更加注重其包装是否符合环保要求。然而,包装过度、包装材料难以降解、包装废弃物处理不当等问题仍然存在[1-2],这造成了极大的资源浪费和环境污染,阻碍了可持续发展的进程,也有悖于“双碳”理念。因此,如何合理地选择绿色包装方案,成为企业亟待解决的问题。
绿色包装方案评价是绿色包装方案选择的重要环节,本质上属于多准则决策问题[3]。其包括决策专家、备选方案、准则和评价信息4个基本要素,一般涉及以下几个步骤:1)构建评价指标体系。包装评价指标包括资源、环保、经济、社会、功能等多个维度的指标。2)评价备选方案。在各准则下每个决策专家对方案的评价标准不一,且其偏好也难以采用精确数值表示,因此概率语言术语集(probabilistic linguistic term set,PLTS)成为决策专家评价方案信息时采用的主要形式[4]。例如在对包装外观进行评价时,决策专家认为其“好”的概率为70%,“很好”的概率30%,此时PLTS能很好地表达评价语言信息和相应的概率信息。3)计算决策专家权重和准则权重。权重的大小会对决策的最终结果产生影响,合理的权重确定方法尤为重要。4)确定方案优序关系。对于准则数量多于方案数量的多准则决策问题,QUALIFLEX是一种非常有效且简便的决策方法[5],其通过对各备选方案进行优劣关系排序找到最优方案。
随着决策环境的复杂化以及决策群体的大规模化,基于社会网络分析(social network analysis,SNA)的群决策方法成为解决决策问题的一种有效方法。在社会网络环境下,决策专家的观点往往会受到其他决策专家观点的影响,决策专家之间的信任关系及网络结构特征会在一定程度上改变原来的决策结果[6]。因此,考虑决策专家之间的信任关系以及决策专家的个人偏好关系,能使决策过程更符合现实情况,获得更具合理性和有效性的决策结果。
因此,本文拟在社会网络环境下,提出一种融合概率语言和QUALIFLEX的多准则群决策方法(SNA-PLTS-QUALIFLEX方法),以解决绿色包装方案评价问题。首先,从资源、环境、经济、功能和社会5个维度确定绿色包装方案评价指标体系;其次,通过PLTS表达决策专家对各方案各准则的评价信息;再引入决策专家间信任关系网络表示决策专家之间的信任关系,以此确定决策专家权重,同时引入决策专家-准则偏好关系矩阵表达决策专家对准则的偏好关系,结合可能度公式计算准则权重;最后,利用QUALIFLEX方法确定备选绿色包装方案的优序关系。
1 方法基础
1.1 概率语言术语集
Pang Q. 等[7]提出PLTS的概念,将多个语言术语及各个语言术语的重要程度均考虑在内,且允许决策专家在评估过程中提供不完整的概率分布信息。PLTS的相关定义及运算规则如下:
定义1[8-9]S={s1,s2, …,sτ}是一个语言术语集,其中τ为奇数。S需满足以下4个条件。
1)有序性:si>sj,其中i>j;
2)负离子:Neg(si)=sj,其中j=τ-i;
3)最大算子:max(si,sj)=si,其中i≥j;
4)最小算子:min(si,sj)=sj,其中i≥j。
定义2[10]S={s1,s2, …,sτ}表示粒度为τ的一个语言术语集。L(p)表示PLTS,其定义为
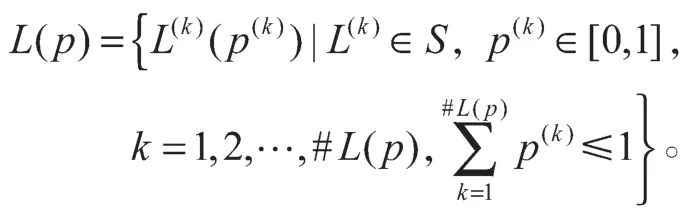
其中:L(k)(p(k))表示决策专家用语言术语L(k)进行评价的概率为p(k);#L(p)表示L(p)中所有不同元素的个数。当时,概率语言信息不完整,需对其进行规范化处理。
定义3[7]设

为一个PLTS,规范化后的PLTS表示为

定义4[11]设L1(p)和L2(p)是两个PLTS,且满足L(p)={L(p(k))|L∈S,p(k)∈[0, 1],k=1, 2, …,#L(p)},分别为L1(p)和L2(p)的下标,则L1优于L2的可能度为,其中
定义5[11]设L1(p)和L2(p)是两个PLTS,且满足L∈S,则L1(p)和L2(p)满足以下运算规则:
1)L(p)的补集定义为

2)L(p)的上下界定义为

1.2 社会网络分析
社会网络分析是基于图论对网络结构进行识别和描述,从而分析网络节点间关系,进而研究网络结构对各节点影响的一种社会学研究方法[12]。图论及网络结构的相关基础知识如下:
社会网络图[13]由G=(V,E)表示,其中V为网络节点的集合,E为节点之间连边的集合。在无向图中,(vi,vj)∈E表示节点vi与vj之间存在关系;在有向图中,表示节点vi指向vj,具体如图1所示。

图1 社会网络图Fig. 1 Social network diagram
网络拓扑结构[14]常用于直观地描述网络中节点之间的连接关系。常见的网络拓扑结构有星型拓扑结构和网状拓扑结构。其中,星型拓扑结构中的网络中心节点与其他节点均有连接关系(如图2a所示),网状拓扑结构基于一定的规则对网络中的节点进行网状连接(如图2b所示)。

图2 网络拓扑结构Fig. 2 Network topology
点度中心度[15]常用于描述网络拓扑结构特征,其大小能够反映网络中节点与中心地位的靠近程度,常分为入度中心度和出度中心度。
在无向图中,Ii=N-1,在有向图中,,其中Ii为i的点度中心度,N为网络中节点的个数,xij为节点i与j的连接情况。若Ii代表入度中心度,则表示指向节点i的连边数;若Ii代表出度中心度,则表示节点i指向其他节点的连边数。
1.3 QUALIFLEX方法
QUALIFLEX方法[16-18]是一种非常有效的基于优序关系的多准则决策方法,能够有效地对决策问题中的基数与序数信息进行处理,且适用于准则数量大于方案数量的情况[5]。
假设有m个决策专家D={dh|h=1, 2, …,m},p个备选方案X={xi|i=1, 2, …,p},n个评估准则C={cj|j=1,2, …,n},使用QUALIFLEX方法对备选方案进行排序的具体步骤如下:
步骤1各决策专家D={dh|h=1, 2, …,m}对各个备选方案X={xi|i=1, 2, …,p}的评估指标C={cj|j=1,2, …,n}给出评价值,获得评价矩阵;
步骤2针对不同决策专家给出的评价信息,利用聚合算子获得综合群体评价矩阵;
步骤3列出p个备选方案存在的p!种可能的排序方案Ol=(…,xi, …,xk, …);
步骤4计算准则权重W={wj|j=1, 2, …,n}和决策专家权重We={weh|h=1, 2, …,m};
步骤5计算准则cj下,第l种测试方案中方案对xi和xk的一致性/不一致性指标;
步骤6计算准则cj下,第l种测试方案的加权一致性/不一致性指标;
步骤7计算第l种测试方案的综合一致性/不一致性指标Il;
步骤8获得方案的最佳排序,最大的Il值对应的测试方案为最佳测试方案,该测试方案下的备选方案排序为最优排序。
2 方法原理
2.1 问题描述
设决策专家集合为D={dh|h=1, 2, …,m},决策专家权重集合为We={weh|h=1, 2, …,m},备选方案集合为X={xi|i=1, 2, …,p},准则集合为C={cj|j=1,2, …,n},准则权重为W={wj|j=1, 2, …,n}, 且,。决策专家个人评价决策矩阵为,其中


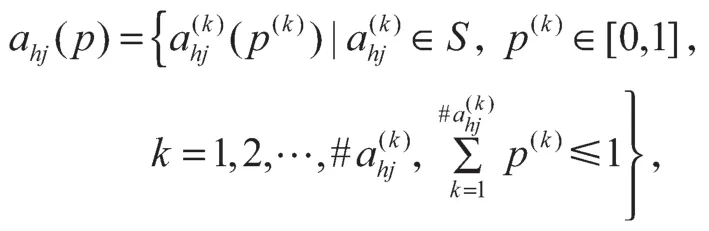
ahj(p)表示决策专家dh对准则cj的偏好值,以PLTS表示。
2.2 方法框架
本文提出的SNA-PLTS-QUALIFLEX绿色包装评价方法分为4个分析阶段,如图3所示。

图3 SNA-PLTS-QUALIFLEX绿色包装评价方法框架Fig. 3 SNA-PLTS-QUALIFLEX green packaging evaluation method framework
第一阶段为评价指标体系确定阶段。通过查阅相关文献及资料,从资源、环境、经济、功能、社会5个维度构建绿色包装评价指标体系。第二阶段为群体综合评价矩阵生成阶段。通过分析决策专家信任关系网络确定决策专家权重,结合各决策专家给出的初始评价矩阵,运用概率语言加权平均(probabilistic linguistic weighted averaging,PLWA)聚合算子生成群体综合评价矩阵。第三阶段为综合一致性/不一致性指标计算阶段。首先通过分析决策专家-准则偏好关系确定准则权重,然后基于群体综合评价矩阵获得各测试方案对的可能度矩阵,从而计算各测试方案的加权一致性/不一致性指标值,最后结合准则权重和加权一致性/不一致性指标值计算各测试方案的综合一致性/不一致性指标值。第四阶段为方案选择阶段。基于综合一致性/不一致性指标值对各测试方案进行排序,确定最优方案。
2.3 评价指标确定
基于可持续发展理念,绿色包装既要满足保护、运输、便利等功能要求,也要符合低危害、低消耗及高环保要求[19]。引入绿色包装评价指标体系,对合理地设计和选择产品包装方案尤为重要,其不仅对判断一个产品的包装方案能否满足绿色要求起作用,还有利于组织管理者做出科学的企业战略决策,并指明产品绿色包装未来发展方向[19-20]。在构建绿色包装评价指标体系时,应结合包装产品的全生命周期即原料选择、制造、使用到废弃全过程,从资源、环保、经济和功能等方面综合分析包装产品是否符合绿色要求。此外,包装产品是为人所用的,而人与社会相互依存相互影响,在评价包装产品时,应充分将人和社会的因素考虑在内。因此,本文将绿色包装评价维度扩展到人与社会层面,构建一个三层绿色包装方案评价指标体系。首先将绿色包装设置为目标层(第一层),其次将资源、环境、经济、功能、社会5个指标设置为评价指标体系中的一级指标层(第二层),最后将一级指标下10个影响程度较大的因素设置为 指标体系中的二级指标层(第三层),如图4所示。
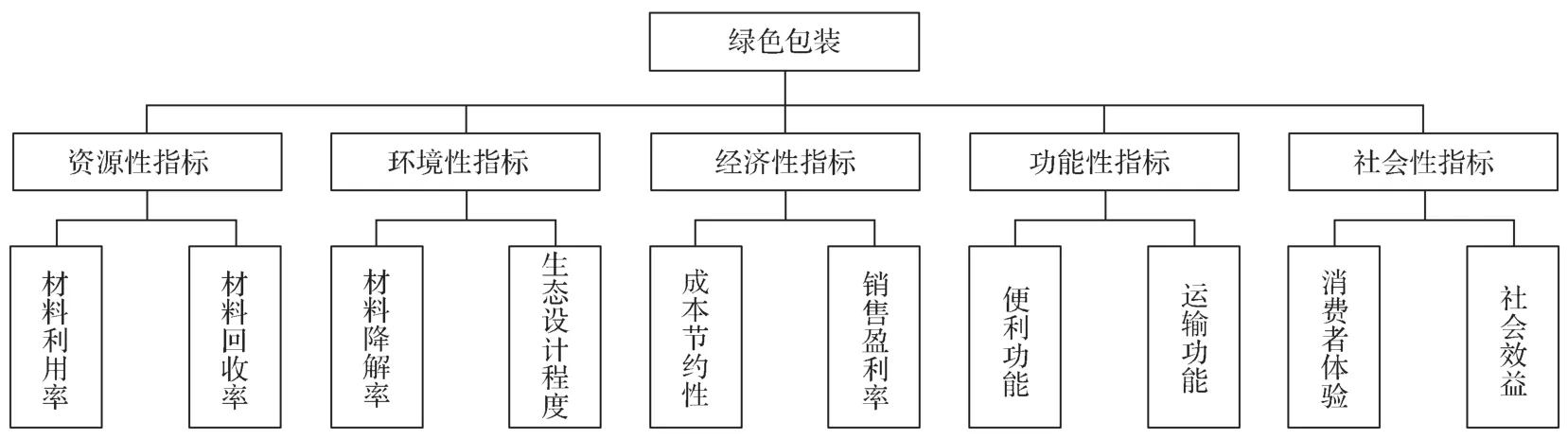
图4 绿色包装方案评价指标体系Fig. 4 Evaluation index system of green packaging scheme
2.4 群体综合评价矩阵生成
2.4.1 专家权重确定
基于社会网络的网络拓扑结构衡量各决策专家的影响力,确定各决策专家的权重,计算公式为

其中Ih为决策专家dh的受信任度,在决策专家信任关系网络中用入度中心度进行计算。
2.4.2 信息集结
聚合算子能够有效地将各个决策专家的评价信息集结为一个综合群体决策专家评价信息矩阵。本文基于PLWA聚合算子,对各个决策专家的评价信息进行聚合。PLWA聚合算子定义[7]为

其中Lh(p)对应的一个权重向量为we=(we1,we2, …,wem)T,且满足。
2.5 综合一致性/不一致性指标计算
2.5.1 准则权重确定
1)偏好矩阵转换
准则偏好函数用F表示,决策专家对准则的偏好评价语言集记为S,则
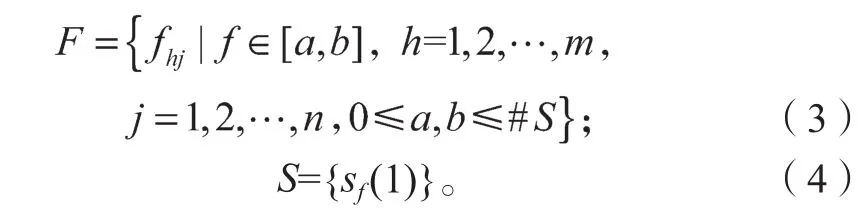
式中:fhj为决策专家h对准则j的评分;
#S为用于描述准则的语言术语集中的术语个数。
例如,决策专家对准则j的评分为5时,将其转化为PLTS形式为s5(1)。
2)权重计算
受文献[11]和[21]的启发,本文提出一种基于可能度公式的准则权重计算方法。

pj为cj优于其他准则的可能度;
wj为准则cj的权重;
ri为Li(p)的下标。
2.5.2 指标值确定
1)测试方案排列
存在方案集X={x1,x2, …,xp},有p!种测试排序方案,Ol代表第l种测试方案:
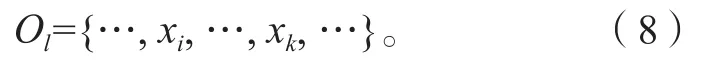
2)基于距离的可能度计算
基于文献[22]提出的可能度公式,对方案对之间的占优关系进行比较,

Li(p)为方案xi的评价信息;
A1为下标之差大于0的集合;
A2为下标之差小于0的集合。
3)加权一致性/不一致性指标值计算
准则cj下,第l种测试方案中方案对xi和xk的一致性/不一致性指标为

准则cj下,第l种测试方案的加权一致性/不一致性指标为

4)综合一致性/不一致性指标值计算
综合一致性/不一致性指标Il的计算公式为

2.6 最优方案选择
基于综合一致性/不一致性指标值Il对最终测试方案进行排序,Il值越大,对应的测试方案越优,基于该测试方案对备选方案的排序,确定最优备选方案xopt:
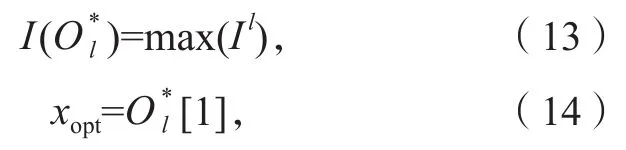
2.7 方法步骤
本文提出的SNA-PLTS-QUALIFLEX绿色包装评价方法共9个步骤,其中步骤1为第一阶段,步骤2~3为第二阶段,步骤4~8为第三阶段,步骤9为第四阶段,具体步骤如下:
步骤1查阅文献资料,确定绿色包装方案评价指标体系;
步骤2基于决策专家间合作次数,构建决策专家间信任关系网络,并在该网络基础上通过公式(1)计算决策专家权重;
步骤3基于各个决策专家对各方案的初始评价矩阵,利用公式(2)生成群体综合评价矩阵;
步骤4利用公式(3)~(4)将将决策专家对准则评分信息转换为准则偏好矩阵;
步骤5基于决策专家-准则偏好矩阵,通过公式(5)~(7)计算各个准则的权重;
步骤6对群体综合评价矩阵,根据公式(8)列出所有测试方案Ol;
步骤7对所有测试方案,根据公式(9)计算准则cj下各方案对的可能度矩阵P;
步骤8利用公式(10)~(12)计算各测试方案的综合一致性/不一致性指标值Il;
步骤9基于综合一致性/不一致性指标值Il,利用公式(13)~(14)对最终测试方案进行排序,确定最优方案xopt。
3 算例分析
3.1 问题背景
对于绿色包装评价问题,主要涉及到产品包装的资源(C1)、环境(C2)、经济(C3)、功能(C4)、社会(C5)5个一级指标,以及10个二级指标,具体包括材料利用率(c1)、材料回收率(c2)、材料降解率(c3)、生态设计程度(c4)、成本节约性(c5)、销售盈利率(c6)、便利功能(c7)、运输功能(c8)、消费者体验(c9),社会效益(c10)。设由绿色包装相关领域的8位决策专家组成的决策群体D={d1,d2, …,d8},基于10个二级指标对x1、x2、x33种绿色包装方案进行评估与优选。决策专家间的合作次数如表1所示。
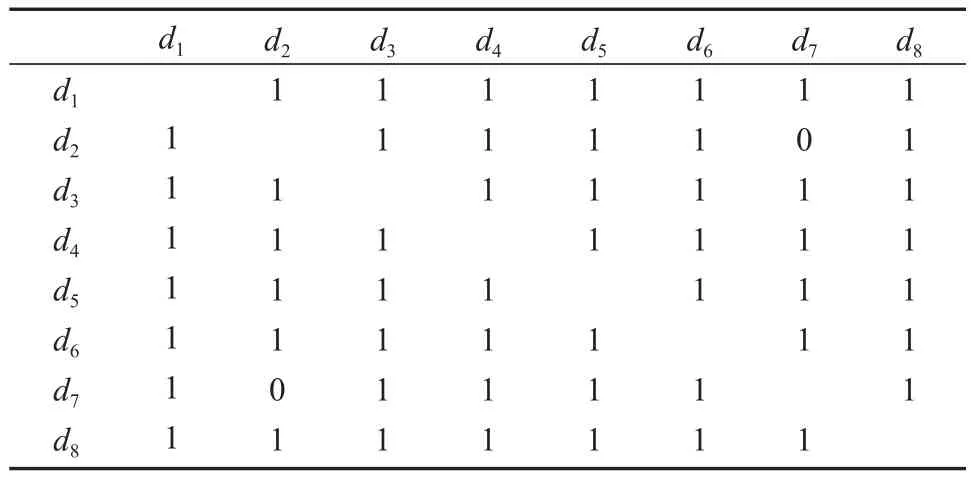
表1 专家合作次数Table 1 Number of cooperation between experts
假设决策专家对方案xi在准则cj下的评价信息由PLTS表示,描述各准则的语言术语集为

当决策专家dh使用PLTS对准则cj下方案xi进行评价时,往往通过多个语言术语及各语言术语对应的概率进行表示,如专家用L(p)={s4(0.6),s5(0.4)}表示其对某个方案某个准则下的评估值为“一般”的概率为0.6,“好”的概率为0.4。限于篇幅,仅给出专家d1对各方案各准则下的评价信息,如表2所示。
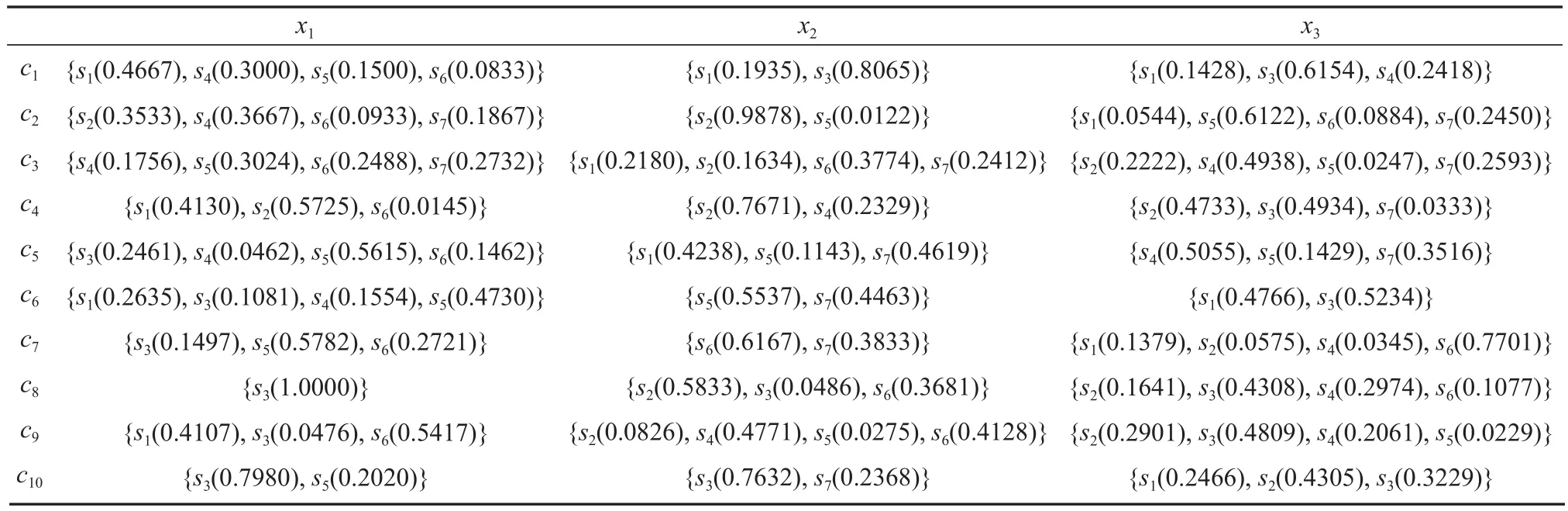
表2 专家d1的评价矩阵Table 2 Evaluation matrix of expert d1
决策专家对不同准则具有不同的主观偏好,其对准则cj的评分结果,如表3所示。

表3 准则得分矩阵Table 3 Criterion score matrix
3.2 决策过程
3.2.1 群体综合评价矩阵生成
基于表1信息,将决策专家间合作关系转换为决策专家间信任关系网络,如图5所示。

图5 决策专家间信任关系网络Fig. 5 Trust relationship network among decision-making experts
基于决策专家间信任关系网络图,根据公式(1)计算得到决策专家权重为

各决策专家基于10个评价准则评估3个备选方案,采用PLTS给出个人评价矩阵,使用公式(2)将个人评价矩阵聚合成一个群体综合评价矩阵,如表4所示。
表4 群体综合评价矩阵Table 4 Group comprehensive evaluation matrix

表4 群体综合评价矩阵Table 4 Group comprehensive evaluation matrix
x1 x2 x3 c1 c2 c3 c4 c5 c6 c7 c8 c9 c10{s1(0.2824), s2(0.1342), s3(0.1528), s4(0.1296),s5(0.0695), s6(0.1019), s7(0.1296)}{s1(0.1080), s2(0.2469), s3(0.0695), s4(0.1389),s5(0.1019), s6(0.1296), s7(0.2052)}{s1(0.0988), s2(0.0972), s3(0.1404), s4(0.0324),s5(0.2315), s6(0.2747), s7(0.1250)}{s1(0.1559), s2(0.1775), s3(0.1065), s4(0.1296),s5(0.1019), s6(0.2160), s7(0.1126)}{s1(0.0325), s2(0.0695), s3(0.1944), s4(0.2052),s5(0.2376), s6(0.1682), s7(0.0926)}{s1(0.3148), s3(0.1358), s4(0.1898),s5(0.1914), s6(0.1034), s7(0.0648)}{s1(0.0972), s2(0.3302), s3(0.1559), s4(0.1019),s5(0.0432), s6(0.0756), s7(0.1960)}{s1(0.1235), s2(0.0756), s3(0.1342), s4(0.1852),s5(0.2392), s6(0.1775), s7(0.0648)}{s1(0.1682), s2(0.1852), s3(0.2006), s4(0.1574),s5(0.0648), s6(0.1312), s7(0.0926)}{s1(0.0556), s2(0.1142), s3(0.3688), s4(0.2006),s5(0.1250), s6(0.0324), s7(0.1034)}{s1(0.1636), s2(0.1559), s3(0.1188), s4(0.2114),s5(0.0756), s6(0.1512), s7(0.1235)}{s1(0.1852), s2(0.0324), s3(0.1312), s4(0.1790),s5(0.2068), s6(0.1574), s7(0.1080)}{s1(0.2562), s2(0.1312), s4(0.2006),s5(0.1358), s6(0.1790), s7(0.0972)}{s1(0.0648), s2(0.1682), s3(0.1188), s4(0.0972),s5(0.1405), s6(0.2377), s7(0.1728)}{s1(0.0988), s2(0.1559), s3(0.1451), s4(0.2438),s5(0.1188), s6(0.1620), s7(0.0756)}{s1(0.2068), s2(0.1404), s3(0.1250), s4(0.0710),s5(0.2176), s6(0.0602), s7(0.1790)}{s1(0.2701), s2(0.3117), s3(0.0694), s4(0.1019),s5(0.0741), s6(0.0972), s7(0.0756)}{s1(0.0602), s2(0.1342), s3(0.1250), s4(0.1682),s5(0.2099), s6(0.1358), s7(0.1667)}{s1(0.1188), s2(0.1512), s3(0.0972), s4(0.0756),s5(0.1899), s6(0.1127), s7(0.2546)}{s1(0.3642), s2(0.0988), s3(0.1080), s4(0.0756),s5(01250), s6(0.0710), s7(0.1574)}{s1(0.1296), s2(0.2716), s3(0.1636), s4(0.1080),s5(0.0648), s6(0.1204), s7(0.1420)}{s1(0.1358), s2(0.1852), s3(0.1034), s4(0.0988),s5(0.2052), s6(0.1744), s7(0.0972)}{s1(0.2654), s2(0.1250), s3(0.1404), s4(0.0695),s5(0.2423), s6(0.1250), s7(0.0324)}{s1(0.1512), s2(0.1204), s3(0.0648), s4(0.2716),s5(0.0648), s6(0.2192), s7(0.1080)}{s1(0.1466), s2(0.1358), s3(0.0756), s4(0.2608),s5(0.1790), s6(0.0278), s7(0.1744)}{s1(0.0926), s2(0.1404), s3(02052), s4(0.1250),s5(0.2315), s6(0.0648), s7(0.1405)}{s1(0.1080), s2(0.1636), s3(0.0926), s4(0.0710),s5(0.2808), s6(0.1914), s7(0.0926)}{s1(0.1852), s2(0.2423), s3(0.1404),s5(0.1528), s6(0.1127), s7(0.1666)}{s1(0.2377), s2(0.1296), s3(0.0432), s4(0.1451),s5(0.1728), s6(0.1682), s7(0.1034)}{s2(0.1296), s3(0.2701), s4(0.1250),s5(0.1559), s6(0.1682), s7(0.1512)}
3.2.2 综合一致性/不一致性指标计算
利用公式(3)~(4),将决策专家对准则的评分信息转换为准则偏好矩阵,如表5所示,矩阵中的偏好信息用PLTS表示。

表5 专家-准则偏好矩阵Table 5 Experts-criteria preference matrix
根据8个决策专家构成的决策群体对10个评价准则进行评分,通过公式(5)~(7)确定各个准则权重为

绿色包装方案的6种可能测试方案Ol(l=1, 2, …,6):(1,2,3)、(1,3,2)、(2,1,3)、(2,3,1)、(3,1,2)、(3,2,1),根据公式(9)得到可能度矩阵P。受篇幅限制,仅给出c1和c10下的可能度矩阵,如表6~7所示。

表6 准则c1下可能度矩阵Table 6 Possibility matrix of criteria c1

表7 准则c10下可能度矩阵Table 7 Possibility matrix of criteria c10
根据公式(10)~(11),获得准则cj下,测试方案Ol下的加权一致性/不一致性指标Ilj,如表8所示。
表8 加权一致性/不一致性指标Table 8 weighted consistency / inconsistency index
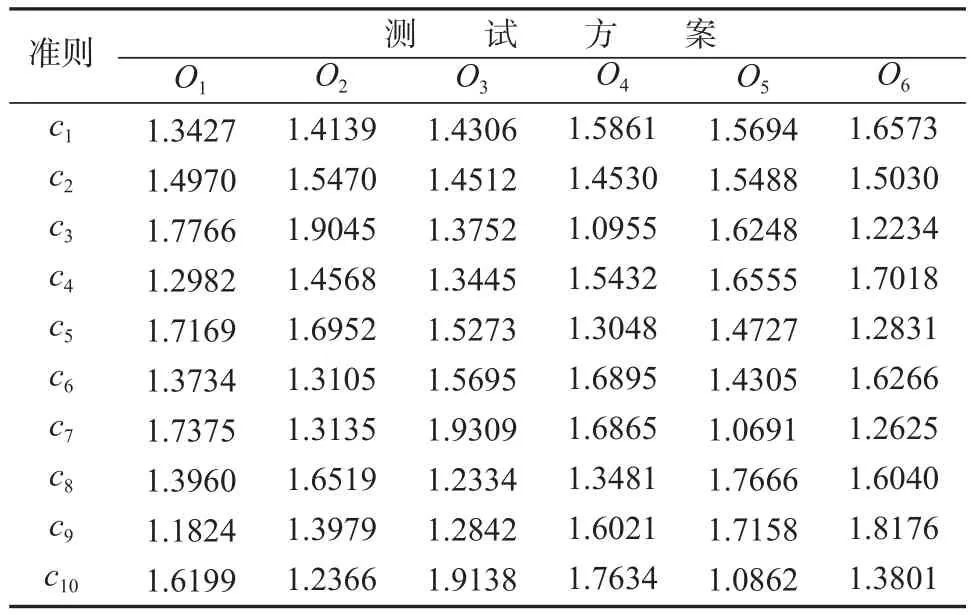
表8 加权一致性/不一致性指标Table 8 weighted consistency / inconsistency index
准则 测 试 方 案O1O2O3O4O5O6 c1 c2 c3 c4 c5 c6 c7 c8 c9 c10 1.3427 1.4970 1.7766 1.2982 1.7169 1.3734 1.7375 1.3960 1.1824 1.6199 1.4139 1.5470 1.9045 1.4568 1.6952 1.3105 1.3135 1.6519 1.3979 1.2366 1.4306 1.4512 1.3752 1.3445 1.5273 1.5695 1.9309 1.2334 1.2842 1.9138 1.5861 1.4530 1.0955 1.5432 1.3048 1.6895 1.6865 1.3481 1.6021 1.7634 1.5694 1.5488 1.6248 1.6555 1.4727 1.4305 1.0691 1.7666 1.7158 1.0862 1.6573 1.5030 1.2234 1.7018 1.2831 1.6266 1.2625 1.6040 1.8176 1.3801
根据公式(12)计算得到各测试方案的综合一致性 /不一致性指标Il:I1=1.5087,I2=1.4957,I3=1.5180,I4=1.5043,I5=1.4820,I6=1.4913。
基于综合一致性/不一致性指标Il,对最终测试方案进行排序,排序结果为

3.3 对比分析
目前,将QUALIFLEX和概率语言相结合的研究较少。文献[23]在概率语言环境下,结合前景理论(PT)对QUALIFLEX方法进行拓展,文献[22]将犹豫模糊语言术语集换为PLTS,提出了一种新的可能度公式及概率语言QUALIFLEX方法。本文利用PLTS表示决策专家群体对各方案的评价信息和决策专家对各评估准则的偏好关系信息,采用QUALIFLEX方法对绿色包装方案进行评估。为证明本文方法的合理性和有效性,将本文方法与文献[22]、[23]的方法进行对比,结果如表9~11所示。

表9 专家权重对比结果Table 9 Comparison results of expert weights
3.3.1 专家权重对比
文献[22]通过计算均值进行赋权,文献[23]未考虑决策专家的权重信息,本文方法基于决策专家之间的信任关系进行赋权,3种方法计算得到的决策专家权重如表9所示。
从表9可以看出,文献[22]认为所有决策专家的影响程度是相同的,文献[23]假设所有决策专家在给出评价信息时就已经达成了一致,这两种方法均未考虑在不同决策问题中,不同决策专家的影响力往往具有差异,这些差异会对决策结果产生影响。相较而言,本文方法对决策专家权重的分配更具有区分度,在绿色包装领域中影响力更大的决策专家在决策时可以发挥更大的作用。因此,本文方法能最大程度地发挥决策专家的专业能力,较以往方法更具客观性和可靠性。
3.3.2 准则权重对比
文献[22]和[23]分别利用线性规划和基于可能度公式的赋权方法确定准则权重,本文方法基于决策专家对准则的偏好关系,利用可能度公式进行赋权。3种方法计算得到的准则权重对比如表10所示。

表10 准则权重对比结果Table 10 Comparison results of criteria weights
由表10可知,在确定准则权重时,文献[22]中各准则分配的权重极不均衡,对c7赋予极高权重1,而认为其他准则的重要性程度极低,权重为0。文献[23]中各准则分配的权重极其均衡,认为所有准则对绿色包装方案决策结果的影响程度相同。相对来说,本文方法对各准则权重的分配更符合现实情况,更具可区分性和可信度。
3.3.3 综合对比
基于本文提出方法中所涉及的社会网络、评价内容、专家权重确定、准则权重确定、方案比较方法5个方面,与文献[22]和[23]中方法进行对比,以说明本文所用方法的特点和优势,综合对比内容如表11所示。

表11 综合对比结果Table 11 Comprehensive comparison results
由表11可知,文献[22]将QUALIFLEX方法和线性规划方法应用于资源规划系统的选择问题,文献[23]将QUALIFLEX方法应用于初创企业的选择问题。其中,文献[22]认为每个决策专家都是同等重要的,并通过求均值的方法赋予每个决策专家同样的权重;文献[23]未考虑决策专家权重问题。然而,在实际中,决策专家之间的信任关系将会对决策结果造成重大影响,故通过社会网络分析计算各个决策专家的受信任程度,以评估其实际影响力和重要性,进而确定各个决策专家的权重,是更加合理的赋权方法。此外,文献[22]和[23]在确定准则权重时,忽略了决策专家对各准则具有不同的偏好,其偏好关系会对决策结果产生直接的影响。因此,结合决策专家对准则的偏好关系与决策专家对各方案各准则的评价信息,得到的准则权重更加符合实际。
4 结语
本文在传统绿色包装评价方法的基础上,充分考虑了决策专家间的信任关系和专家对准则的偏好关系,采用基于信任关系的决策专家赋权方法以及结合偏好关系和基于距离的可能度公式的准则赋权方法,提出了一种SNA-QUALIFLEX-PLTS多准则决策方法,并将其应用于绿色包装方案评价问题。通过与现有研究的对比,本文所提出的方法能够获得更加贴合实际情况、满足决策需求的决策结果,从而实现更加科学合理的决策。本文方法具有如下优点:
1)将绿色包装评价维度进行扩展,构建了一个更加科学合理且符合现实的三层绿色包装方案评价指标体系;
2)采用PLTS对不同方案不同准则下的评价值进行描述,可以较好地体现决策专家在评价时的模糊性特点;
3)通过社会网络分析方法计算专家和准则权重,既减少了计算量,又能体现出决策专家之间的信任关系与决策专家对准则的偏好关系,得到的结果更加全面合理;
4)使用QUALIFLEX方法,一方面能较好处理准则数量大于方案数量的决策问题,另一方面可以降低决策过程的复杂程度,较好地平衡隐性信息利用与决策效率之间的一致性。
在未来的研究中,从以下两个方面进行优化:
1)通过获取真实数据以及不同类型的数据,构建决策专家间的信任关系网络及决策专家对准则的偏好关系矩阵;
2)进一步将决策专家之间的相似关系引入网络构建。

