基于几何约束与隐马尔可夫链模型的轴孔装配策略

潘柏松，颜天野，胡鑫达，罗路平+，翁微妮

(1.浙江工业大学 机械工程学院，浙江 杭州 310014；2.浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310014; 3.博世电动工具(中国)有限公司，浙江 杭州 310052)

0 引言

装配作为零件生产的后续工作，是实现产品功能的主要环节，约占整个生产过程工作量的45%[1]。在电子、计算机等3C行业中，为保证小间隙、易断裂零件的装配精度，常需为装配零件设计专用的定位夹具，使零件定位精度达到亚毫米级，这将大大增加零件装配成本、降低生产效率。

针对零件位姿不确定性导致机器人自动装配效率低、环境适应性差等问题，越来越多学者开始研究机器人自动装配。其中，大部分研究都以轴孔装配为研究对象，因为这一操作代表了装配中的典型困难[2]。HUANG等[3]基于视觉引导，使用百特机器人完成间隙为1 mm的轴孔装配。虽然视觉引导装配效率高、搜索范围大，但其易受环境影响，难以完成亚毫米级别的装配任务，且无法对轴孔间接触力进行控制。因此，大部分针对轴孔装配的研究都引入力传感器，并基于传感器力与力矩信号实现轴孔主动柔顺装配。这些研究[4-6]通常通过建立各接触状态下统计学分类模型或几何、力学物理模型来识别零件接触状态，并根据不同接触状态采用不同运动策略来实现装配任务。ZHANG等[7]通过分析轴与孔零件各接触状态下几何与力学模型的联系，提出一种两步法装配策略，并将该策略应用于低重复定位精度机器人，实现了在22 s内完成0.5 mm间隙的轴孔装配。然而，基于接触状态物理模型的轴孔装配策略对各接触状态识别准确率最高仅为94.4%[8]，仍无法对衔接阶段的接触状态进行精确识别，将大大影响轴孔装配成功率与效率。

近年来，研究人员逐渐采用示教学习[9-10]的方法来实现轴孔装配，以提高不确定性环境下轴孔装配的效率与成功率。与基于接触状态物理模型的轴孔装配相比，XU等[11]指出基于示教学习方法无需进行复杂的在线判断与计算，装配效率大大提高。SONG等[12]应用基于时间的高斯混合模型(Gaussian Mixture Model, GMM)进行示教学习，在20 s内完成间隙为0.18 mm，最大中心距偏差在4.5 mm内的轴孔零件柔顺装配。该方法通过离线学习和在线快速回归拟合控制量，对环境噪声有较好的鲁棒性，但存在对时间的依赖且无法改变机器人速度，机器人停止后难以继续完成装配任务。为避免对时间的依赖性，ALJAZ等[13]利用基于动态运动基元(Dynamic Movement Primitive, DMP)的示教学习方法获得轴孔装配过程中力、力矩信号与机器人运动轨迹的函数曲线对孔轴进行装配。但SONG等[14]实验表明，当轴孔最大中心距偏差与最大轴线夹角从5 mm、1°扩大到8 mm、5°时，基于示教学习的轴孔装配策略装配成功率从100%下降到84%。示教学习方法装配效果依赖于训练样本的选取，在少样本、较大定位偏差情况下，装配成功率无法得到保障。

为克服上述基于接触状态物理模型与基于示教学习数据模型的轴孔装配策略的不足，保证轴孔零件在少训练样本、较大定位偏差情况下装配效率与成功率，本文提出一种将几何约束物理模型与示教学习数据分析方法相结合的机器人轴孔装配策略。该装配策略旨在简化轴孔装配接触状态模型的划分，通过几何、力学物理模型获得轴孔理论装配轨迹，并采用基于隐马尔可夫链模型和高斯混合回归(Hidden Markov Model-Gaussian Mixture Regression, HMM-GMR)[15-16]示教学习模型对装配过程中期望环境接触力进行学习与预测，利用导纳控制器[17-18]对理论装配轨迹进行补偿，实现对期望接触力的跟踪，以保证轴孔零件间稳定的几何约束内接触。本文所提出轴孔装配策略的特点在于通过HMM-GMR模型对期望接触力的跟踪，避免复杂的轴孔装配接触状态划分与识别，以保证在少训练样本、较大定位偏差情况下更高的装配成功率与装配效率。

1 轴孔装配几何与力学分析

为完成轴孔装配任务，一般需要满足以下两个几何条件：①轴孔零件中心距小于配合间隙；②零件轴线平行。由于装配过程中存在夹具定位误差、传感器误差等不确定性因素，零件间的相对位姿难以精确计算。本文根据人类轴孔装配习惯，将轴孔接触状态重新划分，并根据不同接触状态下几何与力学模型，利用传感器力、力矩信号与零件间的几何约束，指导机器人运动，以克服机器人装配过程中不确定性因素带来的零件位姿的偏差。

1.1 轴孔装配接触状态划分

如图1所示，在轴孔装配研究中根据接触点的数量与位置，常将各接触状态[19]分为：①孔外接触阶段,包括孔外单点接触状态、孔外两点接触状态、孔外三点接触状态；②孔内接触阶段,包括孔内单点接触状态、孔内两点接触状态。工程人员在轴孔装配过程中，并不是根据接触点数量识别接触状态，而是通过分辨轴零件发生卡阻的方向调节零件姿态。当装配过程中轴零件受到垂直端面向下的装配力时，轴端底面接触点将产生轴向卡阻，轴圆柱侧面接触点将产生径向卡阻。同时，由于装配力的存在，径向卡阻往往不单独发生。因此，本文将图1中的接触状态重新划分为轴向卡阻状态、轴向径向双向卡阻状态(简称双向卡阻状态)。

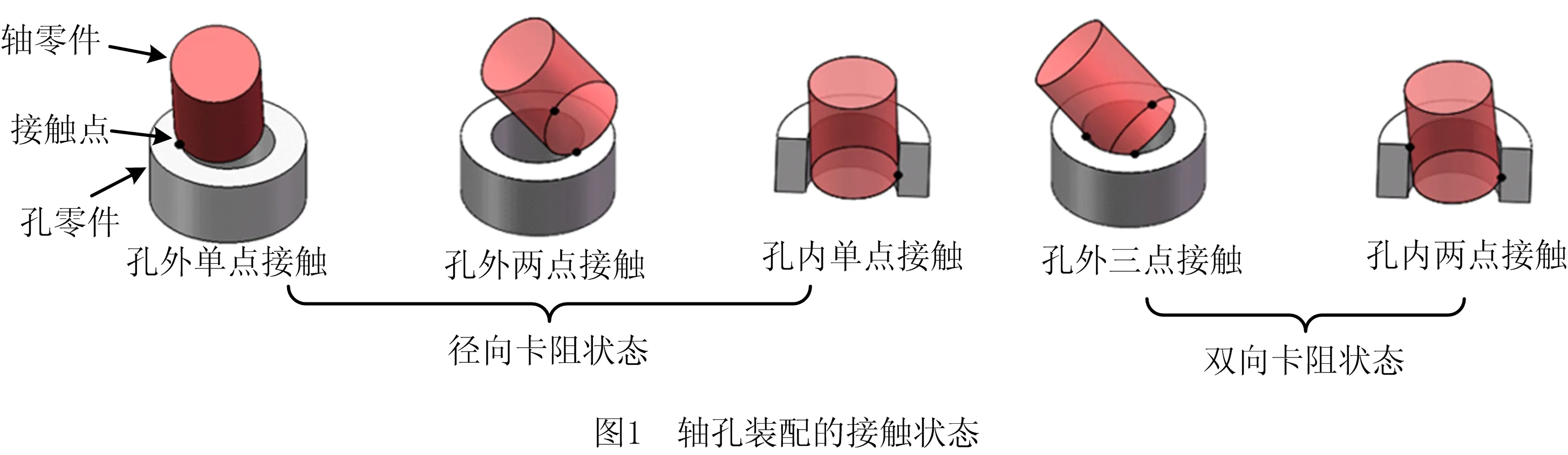
1.2 轴孔装配几何分析

在轴孔装配过程中，将轴插入孔中的深度hZ作为是否完成装配的关键指标。若以轴零件底面圆心作为原点建立坐标系，如图2所示为轴孔零件XoZ面的剖面图，对于直径为d、长度为H的轴零件和孔径为D的孔零件，若设轴孔零件中心点实际距离

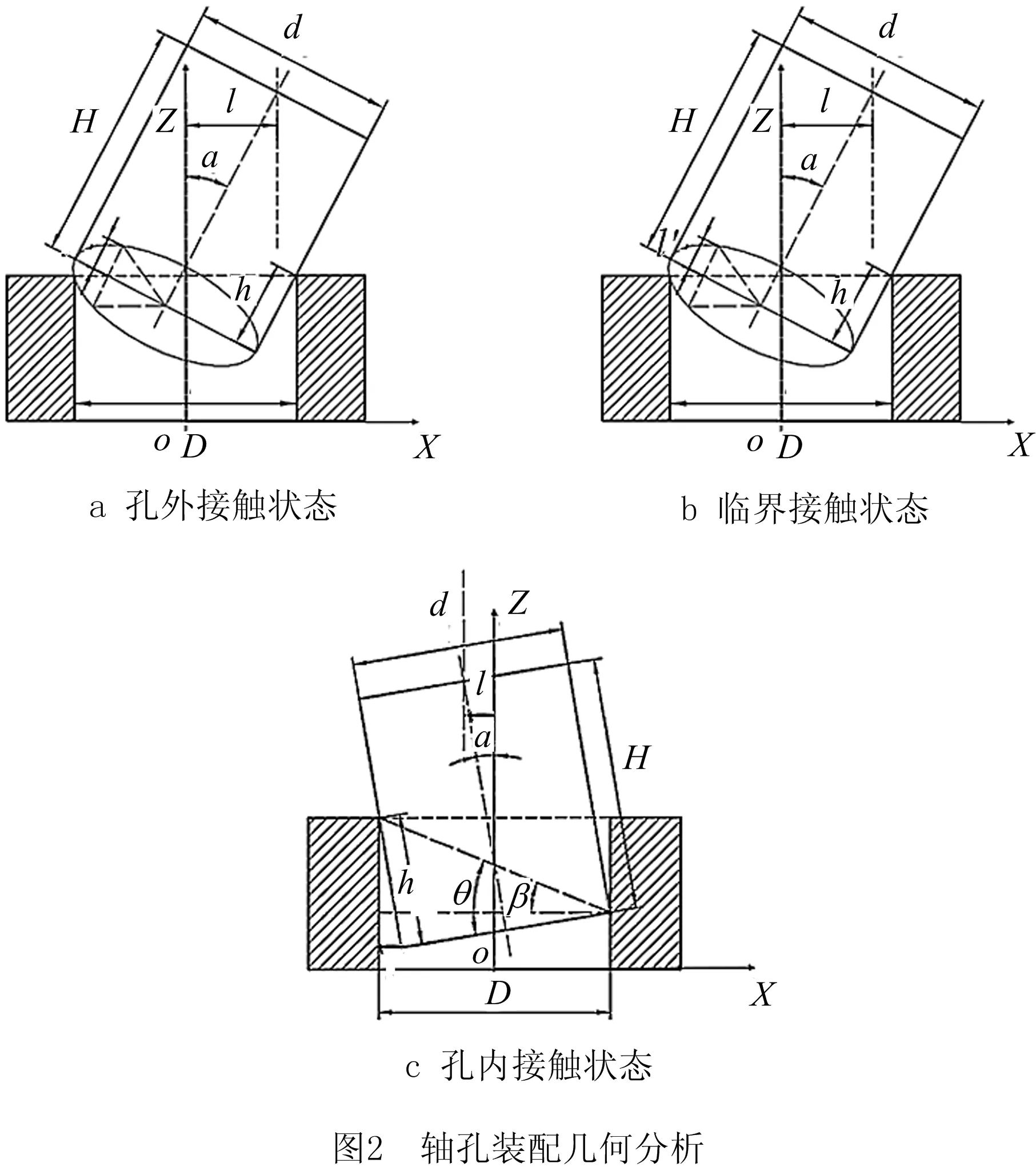
为l，轴孔零件轴线实际夹角为a，轴顶端朝X轴正方向倾斜为正。

根据临界阶段几何分析可知，轴孔装配进入孔内接触阶段时，轴线夹角a最大值amax1的表达式为：

(1)

如图2c所示，轴线夹角a最大值amax2可由图中添加的辅助角θ,β相减计算得到，角θ为轴孔零件孔内接触点相对于轴零件底面夹角，角β为轴孔零件孔内接触点相对于孔零件底面夹角。则轴伸入孔中深度为hZ时，轴孔零件轴线夹角a最大值amax2为：

amax2=θ-β=

(2)

根据式(2)计算，针对小间隙轴孔装配，根据hZ不同,amax2大小往往在0.1°～0.5°之间。

保持零件轴线夹角a不变，轴零件圆柱侧面与孔零件产生接触(进入双向卡阻状态)时，轴插入孔中深度h最大，最大插入深度hmax大小为：

(3)

式中：a≥|amax1|为孔外接触状态，a<|amax1|为孔内接触状态，式(3)可简化为：

(4)

为使轴插入孔中深度最大，零件中心距l与轴线夹角a必须满足：

(5)

当轴插入孔中深度hZ>hmax时，零件中心距l与轴线夹角a必须满足：

(6)

根据式(5)和式(6)绘制函数曲线图3，图中红线为零件发生双向卡阻时中心距l与轴线夹角a的关系曲线，图中黑色区域为轴插入孔中的深度hZ>hmax对应的零件中心距l与轴线夹角a的取值范围。当两零件一直保持端面接触状态时，轴零件平移过程中将在红线处产生径向卡阻。

1.3 轴孔装配力学分析

图4为孔外接触阶段的受力分析，在轴零件上施加一个垂直轴零件端面的装配力FC时，接触点A和B处将产生反作用力FA和FB，对轴零件产生轴向卡阻。此时，反作用力合力F在XoY面的投影总是指向孔的中心。SYLVAIN等[20]指出合力F是轴孔装配即使是在位姿不确定情况下也能顺利完成的重要原因。若轴零件沿合力F方向平移，轴圆柱侧面将与孔零件产生接触，此时轴零件将受到一个阻力f，产生径向卡阻，使轴零件进入双向卡阻状态。

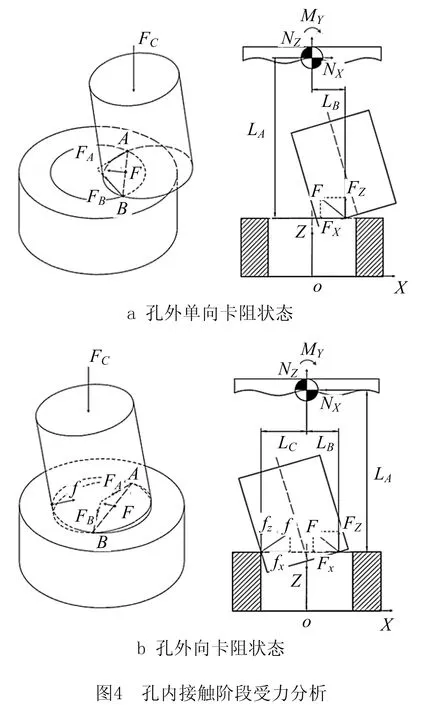
通过受力分析，径向卡阻状态下力传感器X、Z轴方向上力信号NX、NZ和Y轴方向上力矩MY大小可表示为：

(7)

双向卡阻状态下力传感器信号NX、NZ和MY大小可表示为：

(8)

式中：FX、FZ为轴零件底面接触点处产生的合力F在坐标系X、Z轴上的分力;fX、fZ为轴零件侧面接触点处产生的阻力f在坐标系X、Z轴上的分力;LA为轴零件底面接触点到力传感器原点X轴方向上距离;LB为轴零件底面接触点到力传感器原点X轴方向上距离;LC为轴零件侧面接触点到力传感器原点X轴方向上距离。同理，图5为孔内接触阶段的受力分析。轴端面两接触点A和B合并为单点，轴零件发生轴向单点卡阻，其反作用力F在XoY面的投影仍指向孔的中心。若轴零件沿合力F方向平移，轴圆柱侧面将与孔零件产生接触，此时轴零件将受到一个阻力f，产生径向卡阻，使轴零件进入双向卡阻状态。

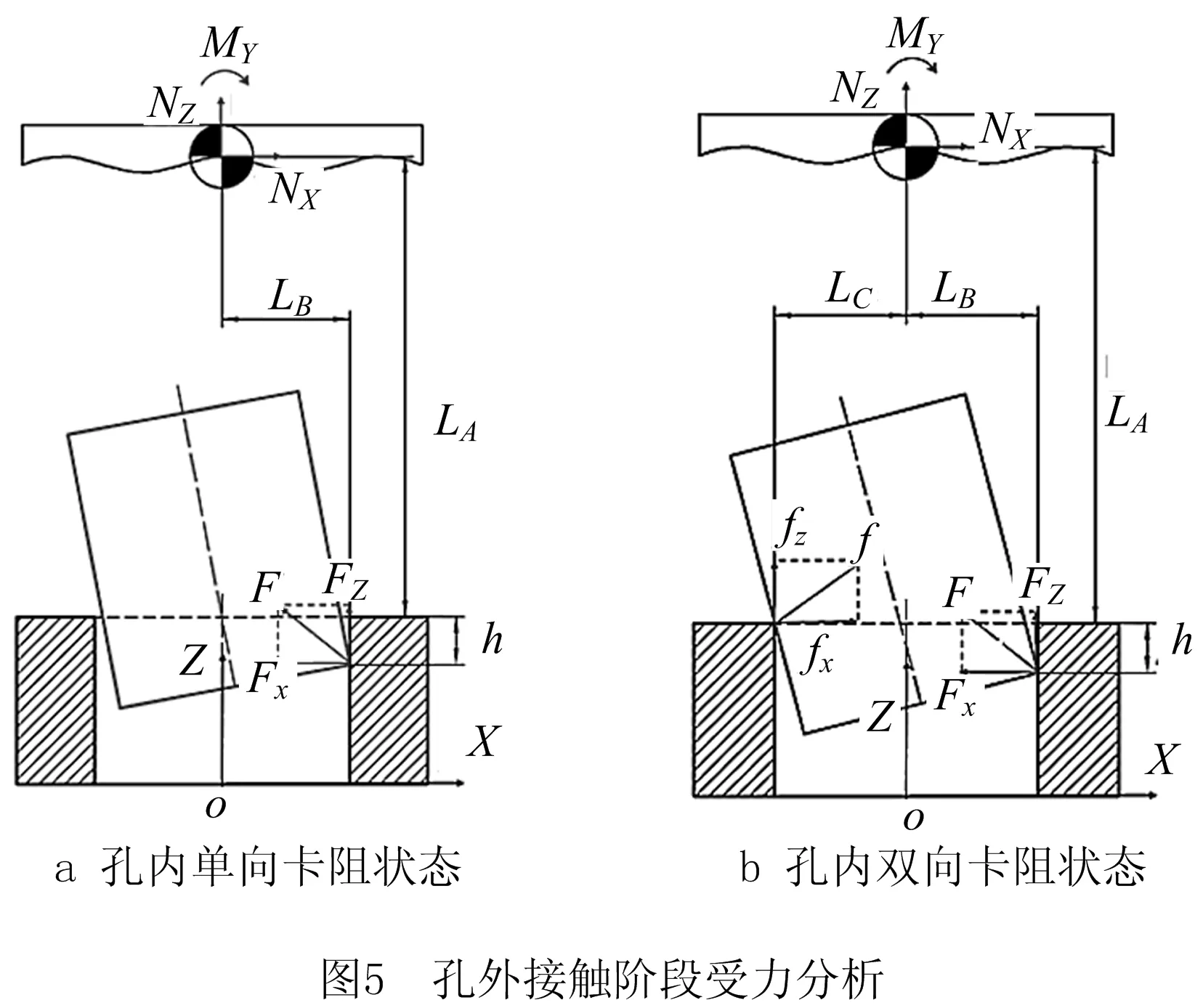
通过受力分析，径向卡阻状态下力传感器信号NX、NZ和MY大小可表示为：

(9)

双向卡阻状态下力传感器信号NX、NZ和MY大小可表示为：

(10)

通过上述对轴孔各接触状态力学模型的分析，当轴孔装配处于轴向卡阻状态时(无论是单点还是多点接触)，接触点处产生的反作用合力F在XoY面的投影指向孔的中心，轴零件沿该合力反方向运动便可到达双向卡阻状态。理论上，由于LA与轴插入深度h已知，且LC+LB=D，整理式(9)和式(10)可得：

MY=-[NX×(LA+h)+NZ×LB]+fZ×D。

(11)

实际情况下，轴孔受力状态更加复杂，且由于传感器误差、重力补偿误差、机械安装误差、轴孔零件尺寸加工误差的存在，传感器力、力矩信号与LC的关系难以定量计算，但由于径向阻力fZ的产生，MY将增大。当前后时刻MY差值ΔMY大于某一阈值时，本文判定轴零件进入双向卡阻的约束状态。

2 约束式轴孔装配策略

为完成小间隙(亚毫米级)轴孔装配，零件轴线夹角a偏差需小于0.5°。若采用经典的基于接触状态物理模型的轴孔装配策略，由于受到诸多不确定性因素的影响，其装配效率与装配成功率将大大降低。本文基于轴孔装配过程中的几何约束，提出一种新的装配策略，来减小装配过程中的不确定性因素对装配效率和装配成功率的影响。

2.1 轴孔装配策略建立

工程人员在闭眼状态下，也能顺利完成较大位姿偏差下的小间隙轴孔装配，其主要是通过分辨零件卡阻方向，利用双向卡阻状态产生的约束阻碍轴零件滑出孔外，从而完成轴孔装配。如图6所示，黑线为本文基于零件间几何约束提出的约束式装配策略理论装配轨迹。当零件发生接触后，仅改变轴孔零件中心距离，零件将从径向卡阻状态转换至双向卡阻状态，再使零件沿双向卡阻状态函数曲线(红线)运动，使零件一直保持双向卡阻状态直至完成轴孔装配。

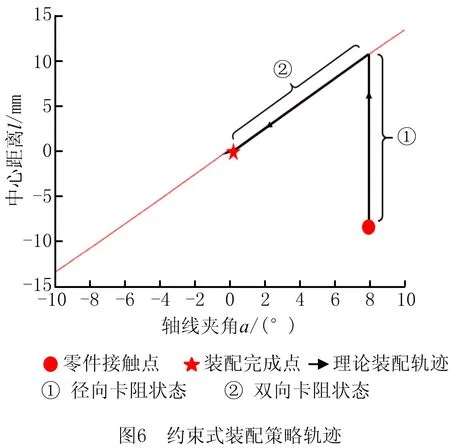
如图7所示，轴零件在产生接触并进入轴向卡阻状态后，沿接触点合力F方向平移，利用轴孔零件间几何约束产生的径向卡阻可克服零件相对位姿的不确定性，若时刻保持双向卡阻状态便能顺利完成装配任务。本装配策略的优势在于，即使轴零件装配过程中产生过量旋转，也可反向平移重新运动至新的双向卡阻状态。

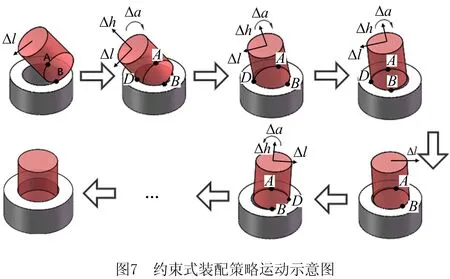
其中，机器人单位时间水平方向与竖直方向位移Δl、Δh与单位时间旋转角度Δa关系式可由式(5)和式(6)得：

(12)

图8为本文所提装配策略的流程图，主要步骤如下：

步骤1机器人运动至装配准备点。

步骤2力传感器置零，装配运行参数初始化。

步骤3机器人沿装配方向缓慢下降Δh直至轴孔产生初步接触，进入轴向卡阻状态，即满足条件1：力传感器Z轴读数NZ大于一定阈值FZ。

步骤4根据力传感器X、Y轴的读数，获得端面接触点合力F的方向和大小，并令机器人沿该方向平移Δl，平移过程中时刻保持传感器Z轴读数NZ大于阈值FZ，直至轴零件进入双向卡阻状态，即满足条件2：前后时刻MX,Y差值ΔMX,Y大于阈值TX,Y。

步骤5记录此时插入深度h′，利用式(5)计算轴线夹角a′，并以此作为a的初始值。令机器人以

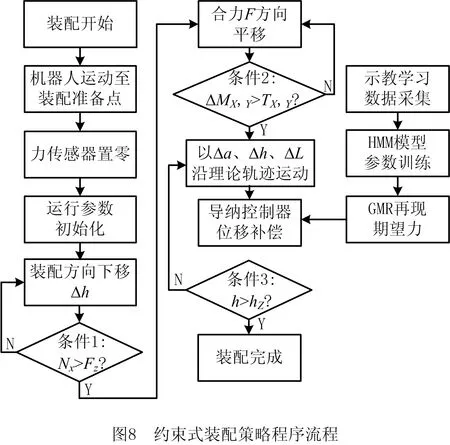
Δa、Δl、Δh沿图6中红色函数曲线运动，并用导纳控制器进行位移补偿，直至满足条件3：轴插入孔中深度h大于hZ。

3 基于HMM-GMR模型的柔顺控制

在实际运行过程中，轴孔装配过程中零件为刚性接触且装配间隙极小。运行参数Δa、Δl、Δh在计算过程产生的偏差将会导致局部接触应力过大或轴侧面、端面脱离接触状态而导致装配失败。因此，本文采用基于HMM-GMR模型的示教学习方法来获得装配过程中的期望接触力Fd，并通过导纳控制器对理论轨迹进行补偿，实现对期望接触力Fd的跟踪，使轴孔零件一直保持双向卡阻状态直至装配完成。

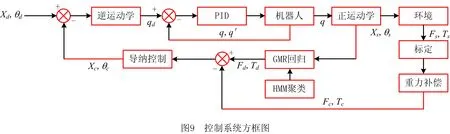
如图9所示，通过读取力传感器数据Fs、Ts后，经标定与重力补偿后得到装配接触力Fc、Tc，将机器人实际位姿Xs、θs输入提前训练好的HMM-GMR模型得到期望力Fd、Td,将其输入导纳控制器获得补偿位姿Xc、θc，并对理论装配位姿Xd、θd进行补偿，经逆运动学与PID控制器控制机器人各轴运动，其中Fd、Td包括笛卡尔坐标下力与力矩{Fd,Td}={FdX,FdY,FdZ,TdX,TdY,TdZ}。

3.1 基于HMM-GMR的示教学习

本文采用HMM-GMR模型对轴孔装配过程中期望接触力进行学习与预测,该方法不依赖时间，且可利用GMR在线回归，对环境噪声有较好的鲁棒性。

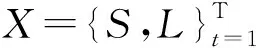
(13)

式中i={1,…,K}。

利用GMR预测期望接触力,接触力的表达式为：

(14)

式中，hi(St)为HMM模型前向向量：

(15)

初始值ht(S1)的表达式为：

(16)

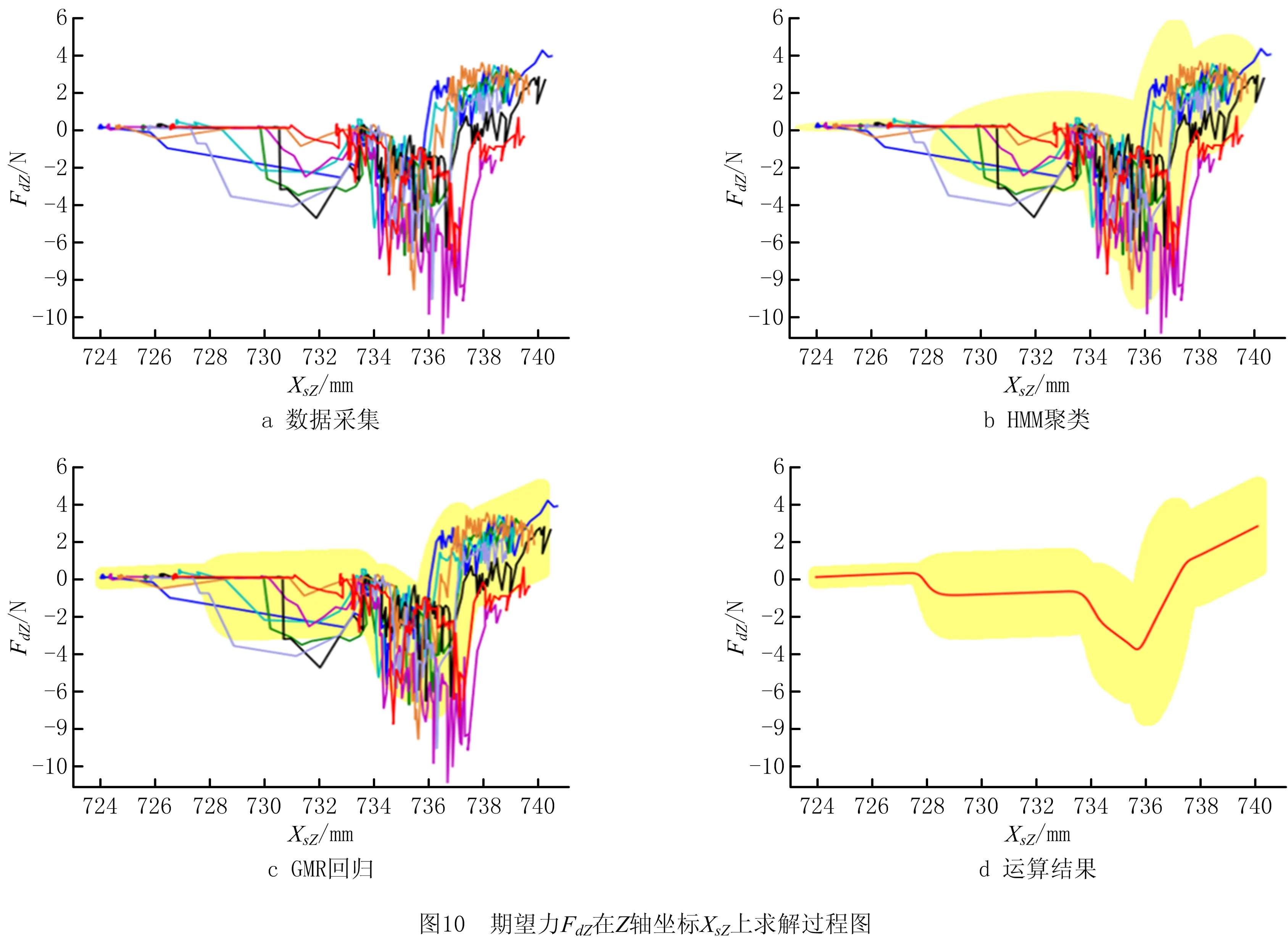
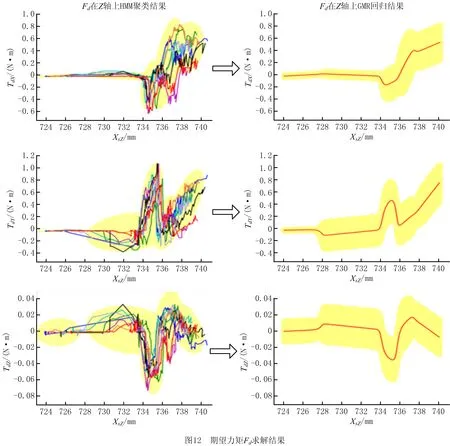
如图10所示，为期望力FdZ在机器人Z轴坐标XsZ上求解过程。图10a为通过机器人拖动示教，完成8组连续序列的数据采集；图10b为利用Baum-Welch算法对HMM模型参数求解，并将数据聚类为5类；图10c为利用式(14)对聚类结果进行GMR回归拟合；图10d为最终运算结果，红线为期望力FZ与机器人Z轴坐标函数曲线，为保证机器人运行的平稳，黄色区域为拟合结果的可信区间，通过多次调参确定最优可信度，这里设置可信度为80%，可通过导纳控制器控制零件接触力在该区间内。

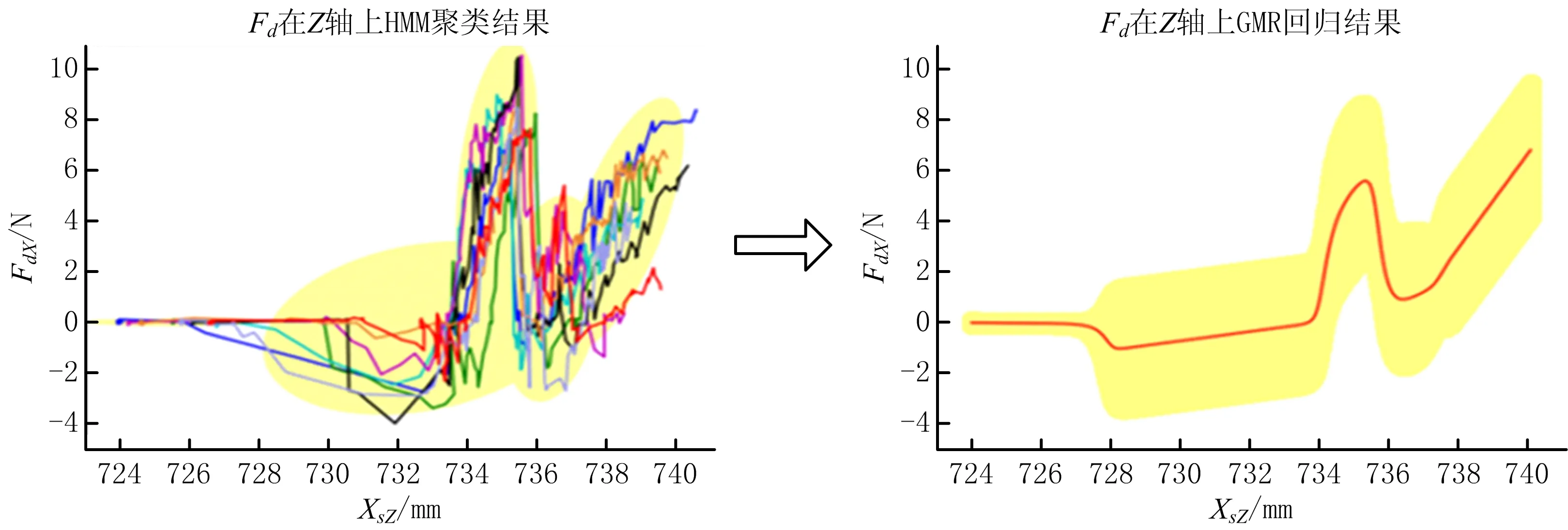
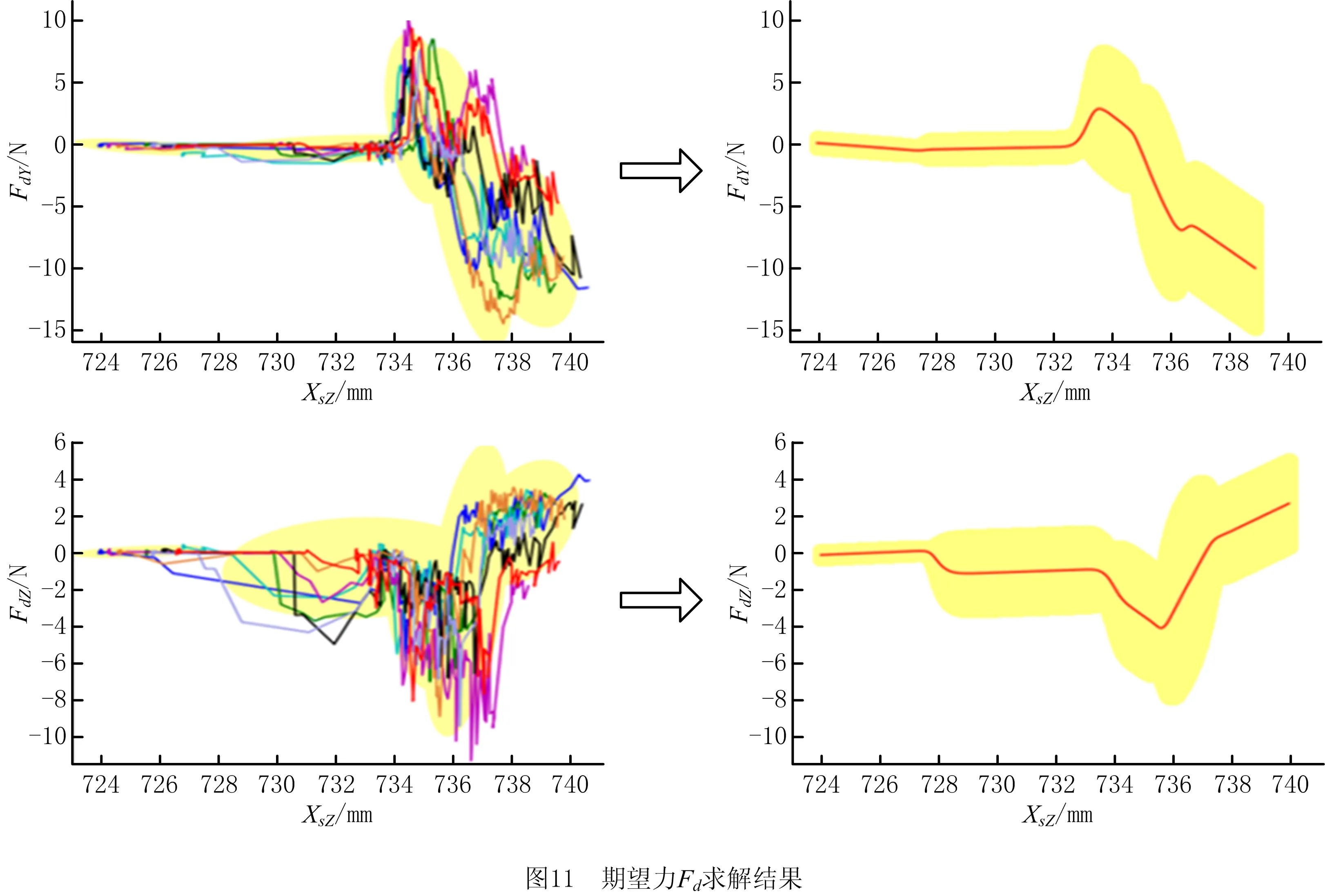
如图11和图12所示，分别为期望力Fd与期望力矩Td在机器人Z轴坐标XsZ上HMM聚类与GMR回归结果。红线为期望力Fd与期望力矩Td与机器人Z轴坐标XsZ回归结果，黄色区域为回归结果的可信区间，可信度为80%。

4 实验与验证

4.1 实验设计

实验平台如图13所示，本文采用ABB 1200工业机器人及三爪气缸、力传感器、相机以及上位机组成机器人轴孔装配系统。基于C#完成程序编写与界面设计，利用USB串口通讯实现力传感器信号的采集，采用机器视觉技术完成零件的识别抓取，通过ABB二次开发实现机器人的控制。

如表1所示，本次实验的装配对象为直径21 mm无倒角圆柱形孔零件与圆柱形轴零件，轴孔零件间隙为0.16 mm，装配深度需大于20 mm，并设定轴孔零件初始中心距偏差为0～15 mm，轴线夹角为0°～10°。

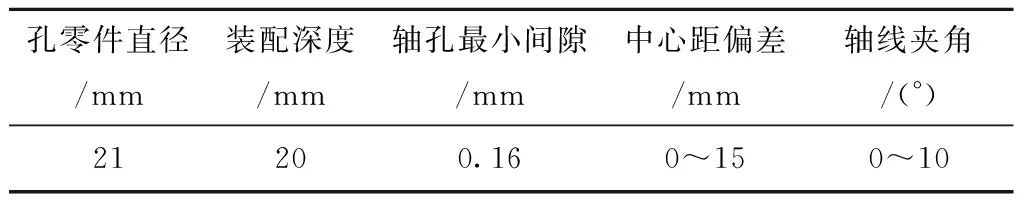
表1 轴孔装配实验对象

为验证本装配策略的有效性，如表2所示设置3组不同策略下的轴孔装配实验。策略一：基于本文所述几何约束与HMM-GMR示教学习方法相结合的轴孔装配策略完成装配；策略二：采用各接触状态下基于几何约束的物理模型与导纳控制器完成装配；策略三：参照文献[12]采用基于时间的GMM-GMR示教学习方法完成轴孔装配。上述实验均采用相同的实验对象与实验环境进行50次重复实验，其中策略一与策略三均采集8组数据进行模型训练。

表2 轴孔装配实验设计

续表2

4.2 实验分析

策略一装配过程如图14所示。图14a为阶段Ⅰ：未接触阶段；图14b为阶段Ⅱ：初步接触阶段；图14c为阶段Ⅲ：轴线卡阻阶段；图14d为阶段Ⅳ：双向卡阻阶段；图14e为阶段Ⅴ：缓慢插入阶段；图14f为阶段Ⅵ：装配完成阶段。

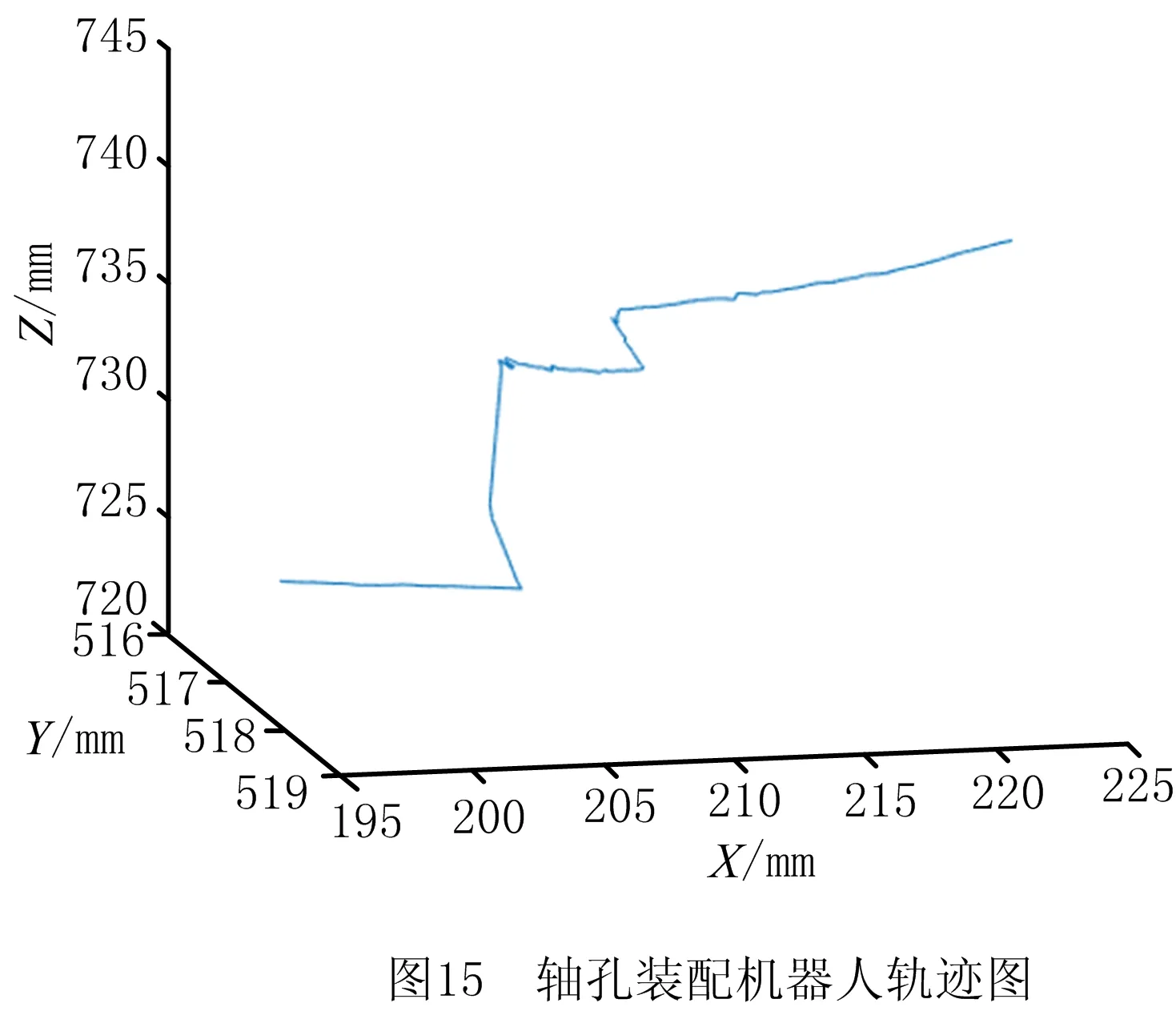
如图15所示为装配过程中机器人轨迹。如图16所示为装配过程中力、力矩与时间之间的曲线。首先，将机器人运动至装配准备点，此时轴孔零件处于阶段Ⅰ，传感器各轴力与力矩读数都为零。机器人沿装配方向移动,经2.7 s进入阶段Ⅱ，传感器产生读数，零件间产生接触。在阶段Ⅲ，零件保持轴向卡阻并沿合力F方向平移，经3.2 s进入阶段Ⅳ。此时，轴零件保持双向卡阻并经6 s的位姿调整进入阶段Ⅴ，在这一阶段传感器力与力矩读数产生较大波动。在阶段Ⅴ，轴零件缓慢插入孔零件中，此时力、力矩信号趋于稳定。当轴零件插入一定深度便到达阶段Ⅵ，轴孔装配完成。

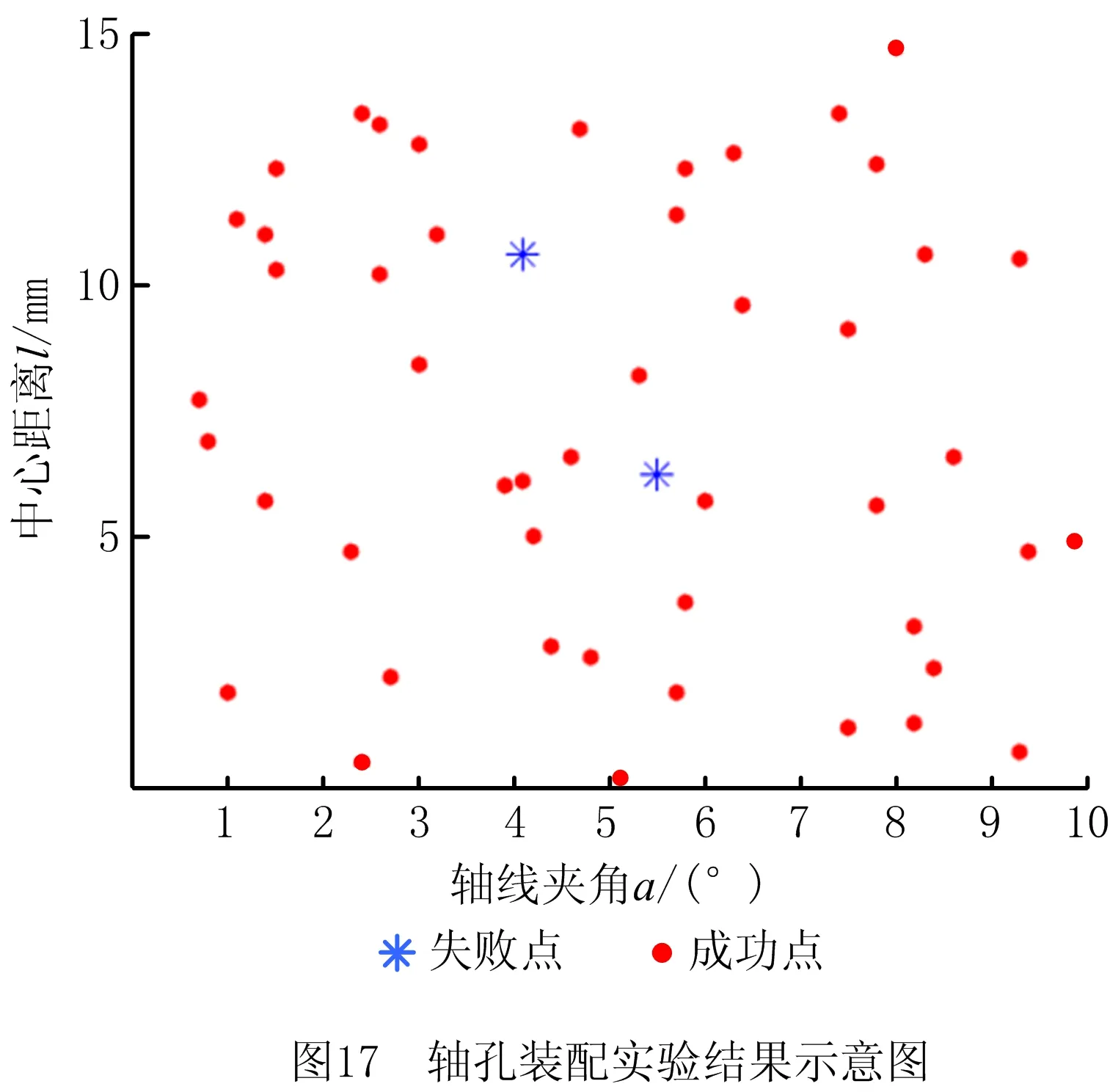
重复50次实验，零件在每次实验中初始位姿偏差随机，并记录实验过程中力传感器读数，当力传感器读数大于50 N视为实验失败。如图17所示，为策略一在零件不同中心距偏差、轴线夹角情况下实验成功与失败情况，在50次实验中共出现2次装配失败,装配成功率为96%。

4.3 实验结果

实验结果如表3所示，可以看到，本文所提出的装配策略一，通过导纳控制器实现了对HMM-GMR模型所求的期望接触力跟踪，保证实际装配过程中精确稳定的接触运动，减少了反复的位姿调整过程，使得在少样本、大定位偏差情况下，装配成功率为96%，平均完成时间为15.1 s，平均最大接触力为14.8 N。基于物理模型的策略二，由于机器人可借助零件间约束，反复进行位姿调整，保证了装配成功率为92%，但正因为反复的计算与调整，平均完成时间达到27 s，平均最大接触力超过29 N。而基于t-GMM示教学习的策略三平均完成时间最短为13.8 s，但由于训练样本相对于偏差范围过少，装配成功率无法保证，仅为64%。从三组实验中可以看出，装配策略三平均完成时间与最大接触力最小，但其不能保证少训练样本、较大零件位姿偏差情况下的装配成功率，本文所提出的装配策略一装配成功率最高，且平均完成时间与最大接触力均小于策略二。

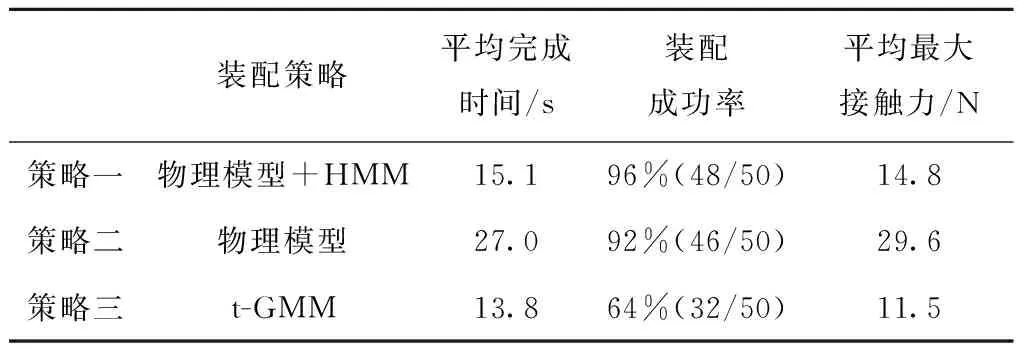
表3 不同策略下轴孔装配实验结果

5 结束语

本文提出一种将各接触状态下几何约束与HMM示教学习方法相结合的机器人轴孔装配策略。首先，对轴孔各接触状态下的几何与力学约束进行分析，获得理论装配轨迹。其次，基于HMM-GMR示教学习方法获得期望接触力与机器人位姿的关系曲线。随后，通过导纳控制器对期望接触力的跟踪，补偿零件间较小的位姿偏差，使零件在约束范围内能够保持稳定的接触运动。最后，针对最小间隙为0.16 mm的轴孔零件进行3组不同装配策略的对照实验。与基于物理模型的装配策略相比，平均完成时间减少约11.9 s，平均最大接触应力减少14.5 N。而与基于示教学习的装配策略相比，保证了在少训练样本、较大零件位姿偏差情况下的装配成功率，装配成功率达96%。在本文中轴孔自动装配对象最小间隙为0.16 mm，仍属于较大的配合间隙，此时零件加工误差对轴孔装配影响较小，故文中主要针对少训练样本、较大零件位姿偏差这一不确定因素，提出了一种新的轴孔装配策略以提高该情况下轴孔装配成功率与效率。而在未来研究中，针对更高精度、更小间隙的轴孔零件，必须进一步考虑加工误差这一不确定因素对机器人轴孔自动装配系统的影响，以提高该情况下轴孔装配成功率与效率。