不确定环境下U型自动化码头绿色集成调度
许波桅,接德培,李军军,杨勇生
(1.上海海事大学 物流科学与工程研究院,上海 201306;2.上海海事大学 商船学院,上海 201306)
1 问题的提出
自动化集装箱码头(简称自动化码头)的高速发展提升了港口的运作效率[1],但是现有自动化码头中场桥需要长距离的往复行驶、能源消耗高;场外集卡司机倒车进入交互区作业时,容易影响其他车道正常通行,在总结现有自动化码头的不足后,上海振华重工提出一种全新U型工艺的自动化码头,如图1所示。U型码头高效经济是未来自动化码头改造的方向[2]。岸桥、自动导引车(Automated Guided Vehicle, AGV)、双悬臂轨道吊(简称轨道吊)和外集卡是U型自动化码头的主要装卸设备,四者相互关联,相互影响,如何使得岸桥、AGV、轨道吊和外集卡高效协同作业,保证以最少的时间完成所有装卸任务,是亟待解决的关键科学问题。

关于自动化码头的集成调度问题,国内外众多学者对此进行了研究,LUO等[3]整合自动化码头装卸设备的各个组成部分,以最小化船舶靠泊时间为目标,建立了混合整数规划模型;常祎妹等[4]考虑龙门吊间的干扰和安全距离等现实约束,建立了龙门吊、集卡和场桥的协同调度模型;田宇等[5]研究了自动化码头双循环AGV和场桥协同调度问题;张振毓等[6]研究了岸侧泊位和岸桥资源的协同调度问题,建立了不确定环境下连续型泊位岸桥集成调度的数学模型,采用双层决策结构的优化算法对模型进行求解;郑红星等[7]研究了传统集装箱码头的场桥和内外集卡的集成调度问题,提出一个多场桥调度整数规划模型,设计新的变异操作来提高遗传算法的全局寻优能力。随着自动化码头建设的加快,如何减少大型自动化装备运作的能耗是另一个重要的科学问题。YU等[8]考虑了工作量的不确定性,研究了集装箱码头中电动轮胎式龙门起重机的碳配置问题,建立了两阶段随机模型;LIU等[9]利用排队论对AGV的运输方式进行建模,通过优化岸桥的数量,使集装箱从岸桥到AGV卸载过程中的碳排放量最小。实际运作中的不确定因素影响着码头的装卸效率,宋云婷等[10]根据集装箱班轮靠泊规则,构建了基于运行时间不确定的集装箱码头靠泊计划优化模型;常祎妹等[11]考虑了集装箱码头岸桥、集卡的速度变化等不确定因素,建立了船舶和集卡装卸作业集成调度模型,并设计了改进的多层遗传算法求解模型;韩笑乐等[12]研究了泊位和堆场资源联合分配问题,考虑了船舶到港时间的不确定性,提出了基于松弛时间的启发式调整规则用来优化启发式算法,为集装箱码头多资源协同分配提供了有效的决策思路。然而,现有自动化码头集成调度研究中,大部分都是建立在确定的理想情况下,较少考虑外集卡;关于集装箱码头节能减排的研究大多数集中在传统码头上,缺乏对自动化码头集成调度情况下的节能减排研究。因此,研究不确定环境下U型自动化码头绿色集成调度有助于促进我国集装箱港口的高质量转型发展。
2 问题描述与建模
2.1 问题描述
本文研究U型自动化码头边装边卸模式,即AGV完成一个集装箱装船任务后接着完成一个卸船任务,完成一个卸船任务后接着完成一个装船任务。在U型自动化码头中,外集卡可以进入堆场与轨道吊进行交互,因此可以将外集卡的任务穿插在AGV任务中,减少外集卡的等待时间,即当外集卡到达时,轨道吊完成当前AGV装卸任务后立即执行外集卡的任务。为了减少轨道吊的行驶距离,降低能耗。本文提出一种绿色等待策略,即当外集卡任务与船舶任务在堆场的贝位一致时,运输该船舶任务的AGV将等待该外集卡到达,之后轨道吊完成外集卡任务装卸后立即对船舶任务进行装卸,可充分减少轨道吊的行驶距离和停驻次数,减少轨道吊的碳排放量。
本文的优化目标为在外集卡到达时间不确定的情况下合理分配作业任务实现岸桥、AGV、轨道吊和外集卡之间集成调度的总时间最小以及3种装卸设备的碳排放最低。
2.2 数学模型
(1)假设
①码头设备之间不存在冲突和拥堵。
②岸桥和AGV间不存在相互等待。
③AGV在转弯和直线行驶的速度相同。
④所有集装箱的大小都为40英尺,外集卡全部为单挂集卡,所运输的集装箱都为40英尺。
(2)符号说明
本文中的符号定义如表1~表4所示。

表1 集合符号定义

表2 参数符号定义

表3 非0-1变量符号定义

续表3
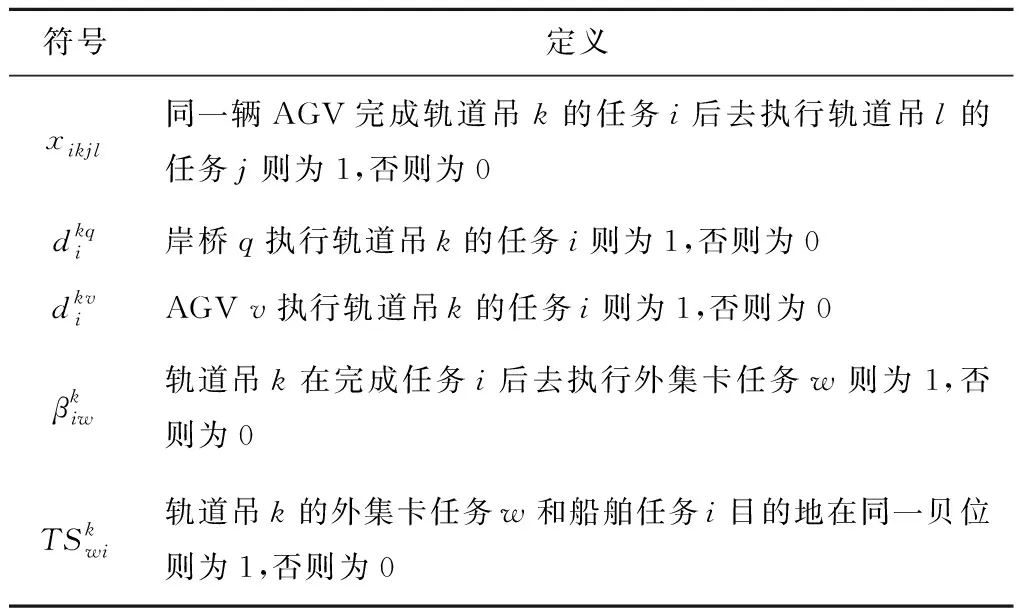
表4 0-1变量符号定义
(3)多目标混合规划模型
(1)
f2=min{Esq+Esy+EAGV},
(2)
f=φ1f1+φ2f2。
(3)
其中:式(1)为第1个目标,码头设备完成所有任务的时间最小;式(2)为第2个目标,3种设备的碳排放量最少;式(3)为目标函数,其中φ1为f1的权重系数,φ2为f2的权重系数。
(4)
(5)
∀k∈Y,i∈U,m∈Q,n∈B;
(6)
∀k∈Y,i∈U,w∈W;
(7)
∀k,l∈Y,i∈U,j∈L,m∈B,n∈B,w∈W。
(8)
其中:式(4)表示卸船任务的开始时刻与AGV到达岸桥时刻之间的关系;式(5)表示AGV到达岸桥时刻与岸桥将集装箱放到AGV上时刻之间的关系;式(6)表示AGV从岸桥出发的时刻与AGV到达堆场指定装卸贝位时刻之间的关系;式(7)表示轨道吊开始卸载AGV上集装箱的时刻与该任务结束时刻之间的关系;式(8)表示上一个卸船任务结束时刻与AGV到达下一个装船任务的堆场指定贝位时刻之间的关系。

(9)
∀l∈Y,j∈L,m∈B,n∈Q;
(10)
(11)
(12)
∀k,l∈Y,i∈U,j∈L,m∈Q,n∈Q。
(13)
其中:式(9)表示装船任务的开始时刻;式(10)表示装船任务开始时刻与AGV到达岸桥时刻之间的关系;式(11)表示AGV到达岸桥的时刻与岸桥将集装箱从AGV上取走时刻之间的关系;式(12)表示岸桥从AGV上取走集装箱的时刻与装船任务结束时刻之间的关系;式(13)表示AGV完成上一个装船任务时刻与到达下一个卸船任务的岸桥的时刻之间的关系。
∀k∈Y,i∈U∪L,w∈W;
(14)
(15)
(16)
(17)
(18)
(19)
(20)
其中:式(14)表示执行与外集卡任务有相同目标贝位的船舶任务的AGV到达目标贝位的时刻与外集卡到达时刻之间的关系;式(15)表示轨道吊到达任务目标贝位的时刻;式(16)表示表示同一辆AGV完成一个岸桥卸船任务后只能完成一个岸桥的装船任务;式(17)表示同一辆AGV完成一个岸桥的装船任务后只能完成一个岸桥的卸船任务;式(18)表示轨道吊一次只能执行一个外集卡任务;式(19)表示一个集装箱只能由一辆AGV运输;式(20)表示一个集装箱只能由一个岸桥装卸。
(21)
C4·ηy2·TN。
(22)
其中:式(21)表示完成所有任务后岸桥总的碳排放量;式(22)表示完成所有任务后轨道吊总的碳排放量。
EAGV=C1·(E1+E2+E3+E4);
(23)
(24)
(25)
(26)
(27)
其中:式(23)表示AGV完成所有任务后总的碳排放量;式(24)表示AGV将集装箱从岸桥运输到堆场的能耗;式(25)表示AGV从堆场行驶到下一个任务堆场的能耗;式(26)表示AGV将集装箱从堆场运输到岸桥下的能耗;式(27)表示AGV从岸桥行驶到下一个任务岸桥的能耗。
(28)
(29)
式(28)~式(29)表示部分参数和决策变量的取值范围。
3 改进的混合遗传布谷鸟算法
3.1 概述
遗传算法是由美国的HOLLAND[13]于20世纪70年代提出的一种启发式算法,由于其通用性强,算法收敛速度快,被大量的学者用于求解自动化集装箱码头的集成调度模型。LAU等[14]以岸桥、AGV和场桥3种设备为研究对象,建立了最小化岸桥延误时间、AGV和场桥总运行时间的集成调度模型,并采用最大匹配遗传算法进行求解;JI等[15]研究了边装边卸模式下的自动化集装箱码头中岸桥、AGV和场桥的集成调度问题,以所有集装箱完成时间最小为目标建立了双层规划模型,并提出基于冲突策略的双层自适应遗传算法解决该协同调度问题;LUO等[3]整合集装箱自动化码头装卸设备的各个组成部分,以最小化船舶靠泊时间为目标,建立混合整数规划模型,提出一种自适应遗传算法。但是遗传算法易早熟,易陷入局部最优解,针对这些缺点,本文引入布谷鸟算法中的莱维飞行搜索方式。布谷鸟算法是于2009年提出的一种新兴启发式算法,其被证明具有较好的全局搜索能力[16-17],使得遗传算法不易陷入局部最优解。除遗传算法以外,李静等[18]利用灰狼优化算法解决自动化集装箱码头AGV的调度问题。
3.2 编码
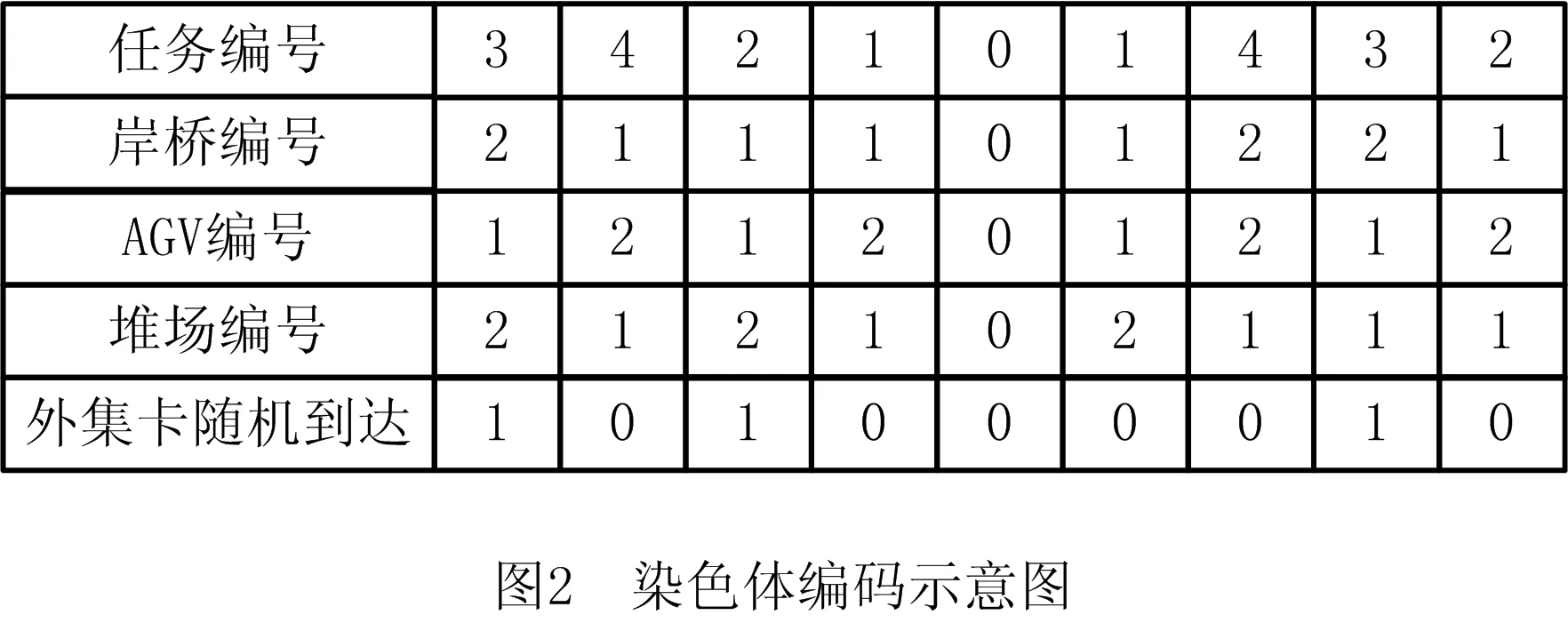
染色体编码是遗传算法的关键操作,染色体编码的好坏直接影响算法的求解结果以及效率。本文研究U型自动化集装箱码头中4种设备的集成调度,因为所建立的模型需要区分岸桥、AGV、轨道吊和外集卡的任务,所以采用任务分配的形式进行染色体编码。假设现在有装船任务和卸船任务各4个,2台双小车岸桥,2辆AGV,2个堆场区域,每个堆场区域配备2台双悬臂轨道吊,染色体编码示意图如图2所示。为了区分卸船和装船任务,本文在染色体中加入数字“0”用来区分,“0”左边的为卸船任务,右边的为装船任务。第1行表示集装箱任务的编号,第2行表示岸桥的编号,第3行表示AGV的编号,编号为奇数的AGV先进行卸船任务后进行装船任务,编号为偶数的AGV先进行装船任务后进行卸船任务,第4行表示堆场的编号,第5行表示外集卡随机到达,其中数字“1”表示有外集卡到达,“0”表示没有外集卡到达。
3.3 解码
对图2染色体进行解码操作,1号AGV路径为:岸桥2→堆场2(卸船任务3)→堆场2→岸桥1(装船任务1)→岸桥1→堆场2(卸船任务2)→堆场1→岸桥2(装船任务3);2号AGV的路径为:堆场1→岸桥2(装船任务4)→岸桥1→堆场1(卸船任务4)→堆场1→岸桥2(装船任务2)→岸桥1→堆场2(卸船任务1)。同理可以得到2号AGV的路径。对于外集卡任务,轨道吊执行完当前任务后立即执行外集卡任务,例如当外集卡随机到达为“1”时,堆场2的轨道吊在执行完卸船任务3后立即执行外集卡任务,外集卡随机到达为“0”时,轨道吊执行完当前任务后继续执行下一个AGV的任务。
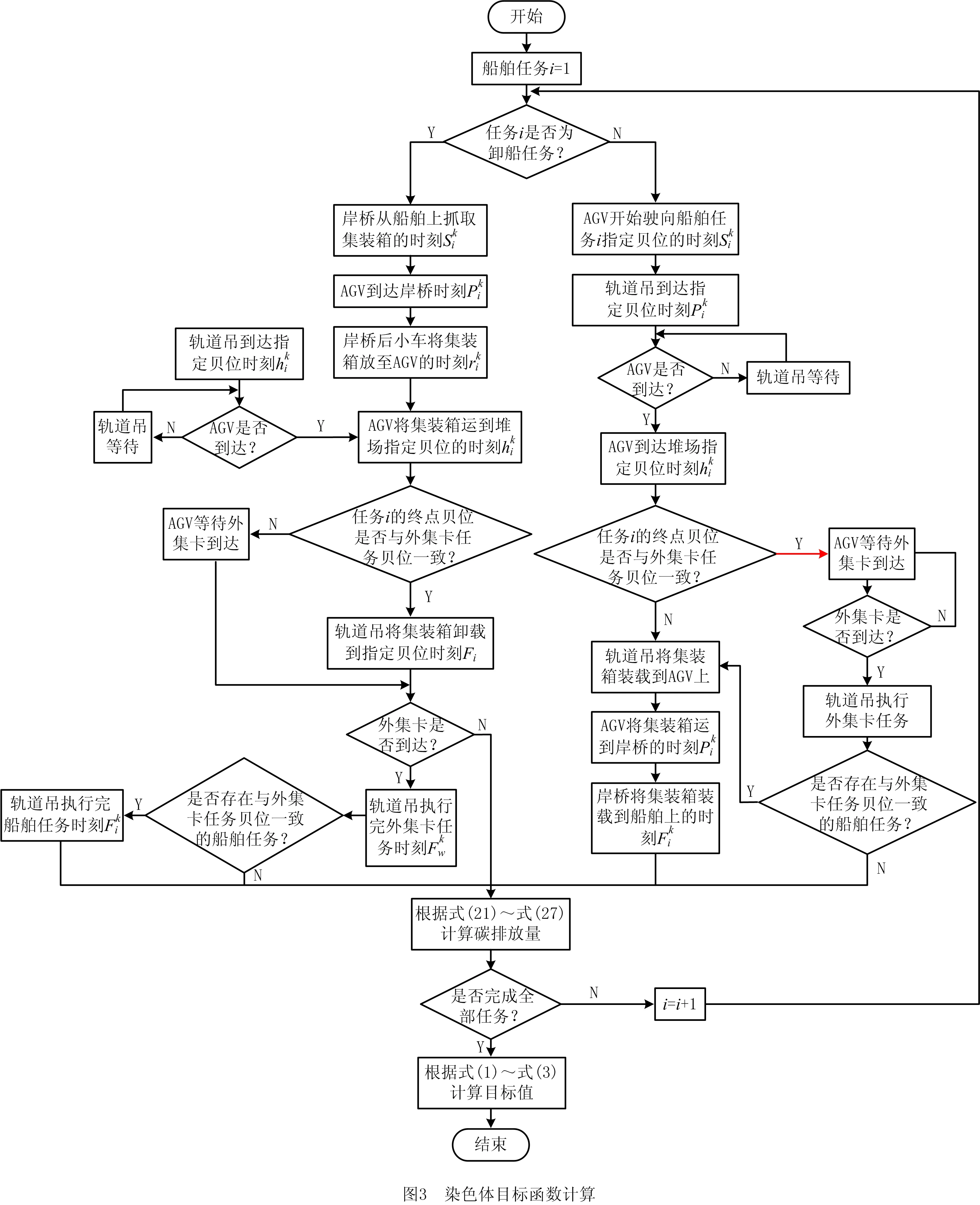
完成任务分配之后,求解目标函数,求解流程图如图3所示。
3.4 基于莱维飞行的交叉
本文的适应度函数选取目标函数的倒数,即F(x)=1/(φ1f1+φ2f2)。选择操作采用轮盘赌机制,为了防止算法陷入局部最优解,本文在选择操作时保留5%的劣质个体。产生下一代可行解采用交叉和变异的方式,其中交叉部分引入莱维飞行的理论,针对染色体第一层任务编号,将染色体中卸船和装船任务分别进行如下操作,首先对每一个基因按照文献[17]的莱维飞行公式进行更新,如式(30)~式(31)所示。
(30)
(31)

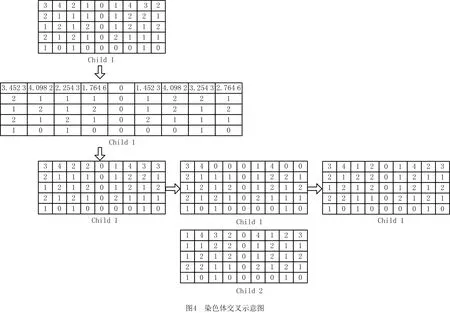
此操作的结果会产生不可行解,随后将不可行解修复成可行解,如图4所示,具体操作为对每个基因位中的元素进行四舍五入取整的操作,然后将其中相同的元素置0,最后选择种群中适应度最好的个体与更新后的个体进行比较,将随机选择的个体中含有但更新后个体中不含有的元素依次替换掉后者中的“0”元素。针对染色体第二、四和五层,将染色体进行单点交叉,随机选择交叉点,将两条染色体交叉点之前或者之后的所有元素进行交换。针对染色体第三层,由于AGV可以进行任意的任务,不需要对第三层进行操作。
3.5 变异
本文的变异采用逆序操作,该操作不会产生不可行解,在染色体上随机选择两点,将两点之间的任务进行逆序排列。变异概率采用自适应变异概率[19],根据进化代数自动调整,如式(32)所示:
(32)
式中:pmax为最大变异概率,pmin为最小变异概率;iter为进化代数,Maxiter为最大进化代数。
3.6 算法流程
改进的混合遗传布谷鸟算法步骤如下:
步骤1初始化。设置参数,根据上述3.2节中的方式生成初始种群。
步骤2计算适应度和选择。根据上述3.3节至3.4节的方式计算适应度并进行选择操作,记录当前最优解。
步骤3交叉操作。根据上述3.4节的方式进行基于莱维飞行的交叉操作。
步骤4变异操作。根据上述3.5节的方式进行变异操作。
步骤5更新当前最优解,若满足停止条件(达到最大进化代数),输出最优解;否则,转步骤3和步骤4操作产生的下一代种群,转步骤2继续寻找最优解。
4 数值实验及结果分析
本章对所建立的模型以及提出的算法进行实例验证,运用MATLAB 2018b,运行环境为Window10操作系统,Intel(R)Core(TM)i7-8750H CPU @ 2.20 GHz,16 GB内存。
4.1 参数设置
(1)模型参数
本文以U型自动化码头中某次船舶靠港装卸为例,码头的布局如图1所示,码头的水平运输区域长300 m,宽120 m,堆场一个贝位的长度为15 m,每个堆场区域有40个贝位。AGV匀速行驶速度为5 m/s,轨道吊匀速行驶速度为2 m/s。岸桥的前小车从船舶上取箱或者将中转平台上的箱子放到船舶上的时间服从(20 s,30 s)的均匀分布,岸桥的后小车将集装箱放到AGV或从AGV上取箱的时间均为20 s,双悬臂轨道吊将箱子从AGV拿到指定堆存点或者从指定堆存点放到AGV上的时间服从(30 s,50 s)的均匀分布,目标函数中的φ1和φ2如式(32)所示:
(32)
岸桥、AGV和轨道吊的作业能耗等相关参数[1]如表5所示。关于碳排放量的计算,本文先计算出装卸设备的电力能耗,再将能耗根据碳排放因子折算成碳排放量,其中碳排放因子选取我国南方区域电网基准线碳排放因子,如表6所示。

表5 设备能耗参数
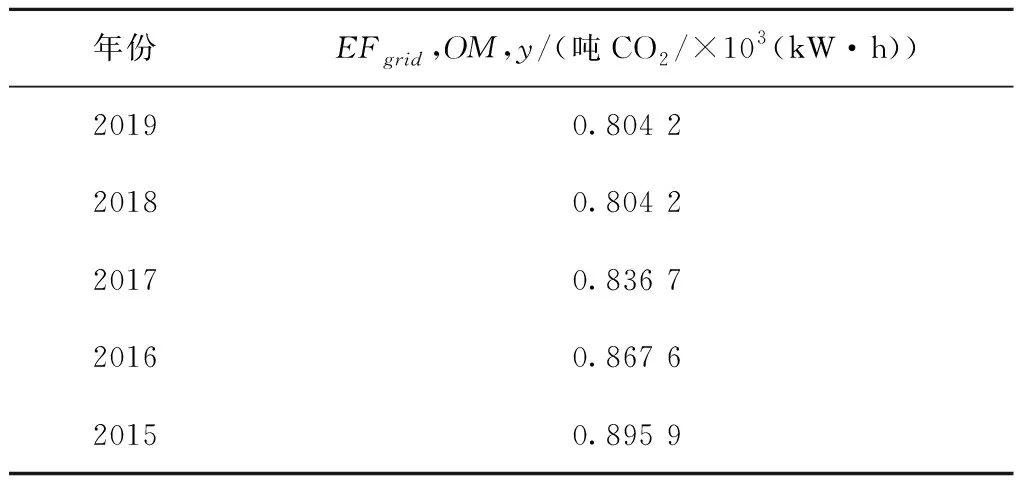
表6 中国南方区域电网基准线碳排放因子
(2)算法参数
算法参数取值如表7所示。

表7 算法参数取值
4.2 结果分析
为了验证模型和算法的有效性,本文分别采用自适应遗传算法(Adaptive Genetic Algorithm, AGA)[3]、遗传算法(Genetic Algorithm, GA)、灰狼优化算法(Grey Wolf Optimizer, GWO)[16]、改进的混合遗传布谷鸟算法(Hybrid Genetic Algorithm Cuckoo Search, HGACS)进行15组对比实验,对于每组实验求解30次,以平均值作为最终的结果,如表8和表9所示。从实验结果可以看出:
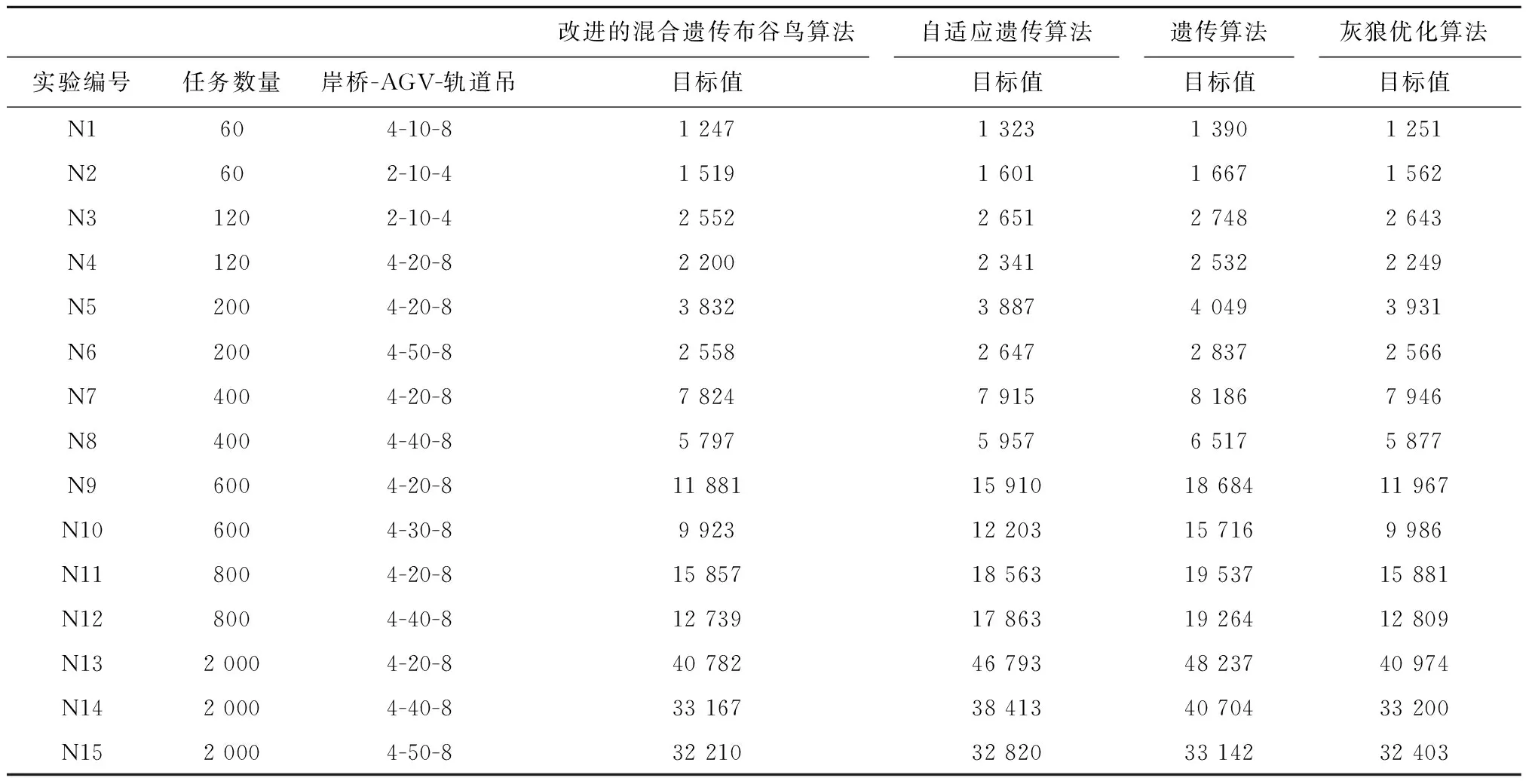
表8 平均目标值的对比

表9 CPU平均运行时间(s)的对比
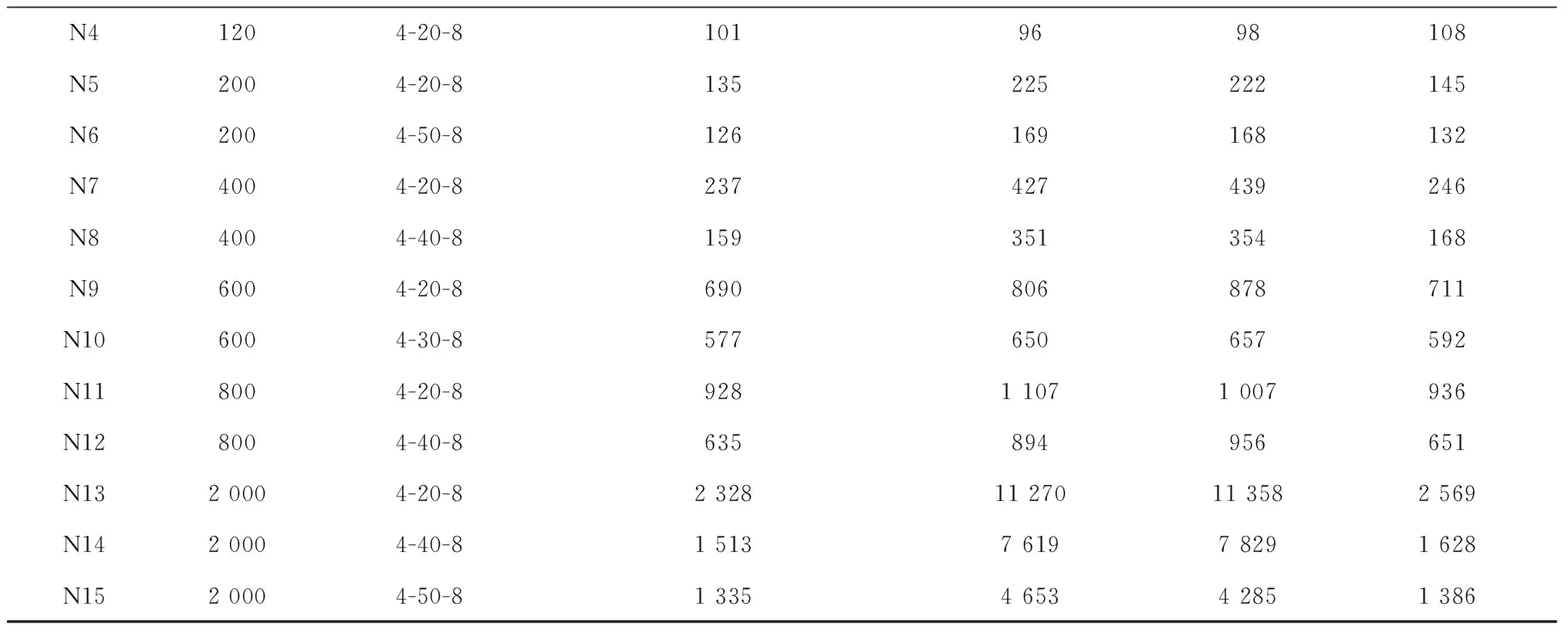
续表9
(1)提出的改进的混合遗传布谷鸟算法在求解过程中,能够稳定地获得大规模集装箱计算问题的近似最优解。例如表9中的算例12和15,在集装箱任务为800、AGV数量为40时,其CPU计算时间大约为15分钟,表8中可以看出其目标值为12 739。当集装箱任务为2 000,AGV数量为50时,其CPU计算时间约为21 min,其目标值为32 210,基本符合现阶段自动化码头作业系统调度的时间和能耗。
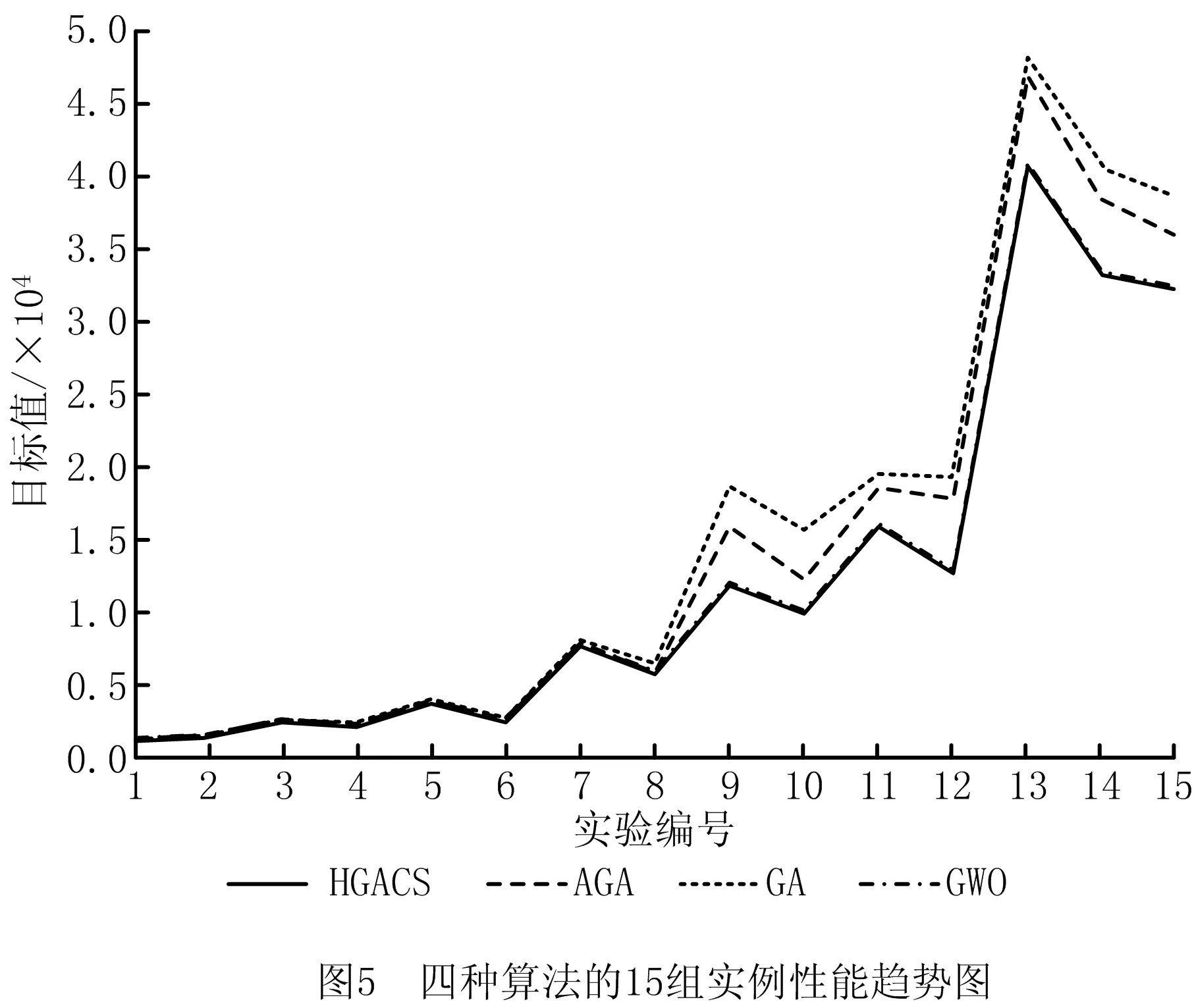
(2)当集装箱任务增多时,码头的总装卸时间也随之增加;同等任务数时,AGV的数量增加会使得总装卸时间减少,因此在一定程度上增加AGV的数量可以显著提高装卸任务的效率,尤其是在大规模集装箱任务时。不同的集装箱任务数以及AGV数量对码头总装卸时间有着显著的影响。如图5所示为4种算法分别计算不同任务数以及不同AGV数量时的最优目标值,比较结果表明在任务数量较小时,几种算法的最优值相近,随着任务数量的增加,本文所实验的其他算法目标函数值与HGACS算法的目标值的差值越来越大。
如图6~图7所示分别为针对小规模算例和大规模算例两种策略的结果对比,从图中可以看出,当任务规模较小时,不等待的策略的结果较好,并且随着任务量的增多,两者的差值逐渐减小;当任务规模较大时,采用等待策略的结果较好,并且随着任务量的增多,两者的差值逐渐增大。产生这种情况的原因是当任务规模小时,码头设备资源利用量较小,碳排放量少,采用等待的策略会导致AGV的运行效率降低,延长任务总完工时间,而目标函数包括总完工时间和能耗两方面,此时总完工时间占比较大,最终导致目标函数值升高。当任务规模较大时,码头资源利用量较大,碳排放量多,采用等待策略可以充分减少轨道吊的行驶距离和停驻次数,减少码头的碳排放量,此时由于碳排放量增多,能耗占比较大,最终导致目标函数值降低。

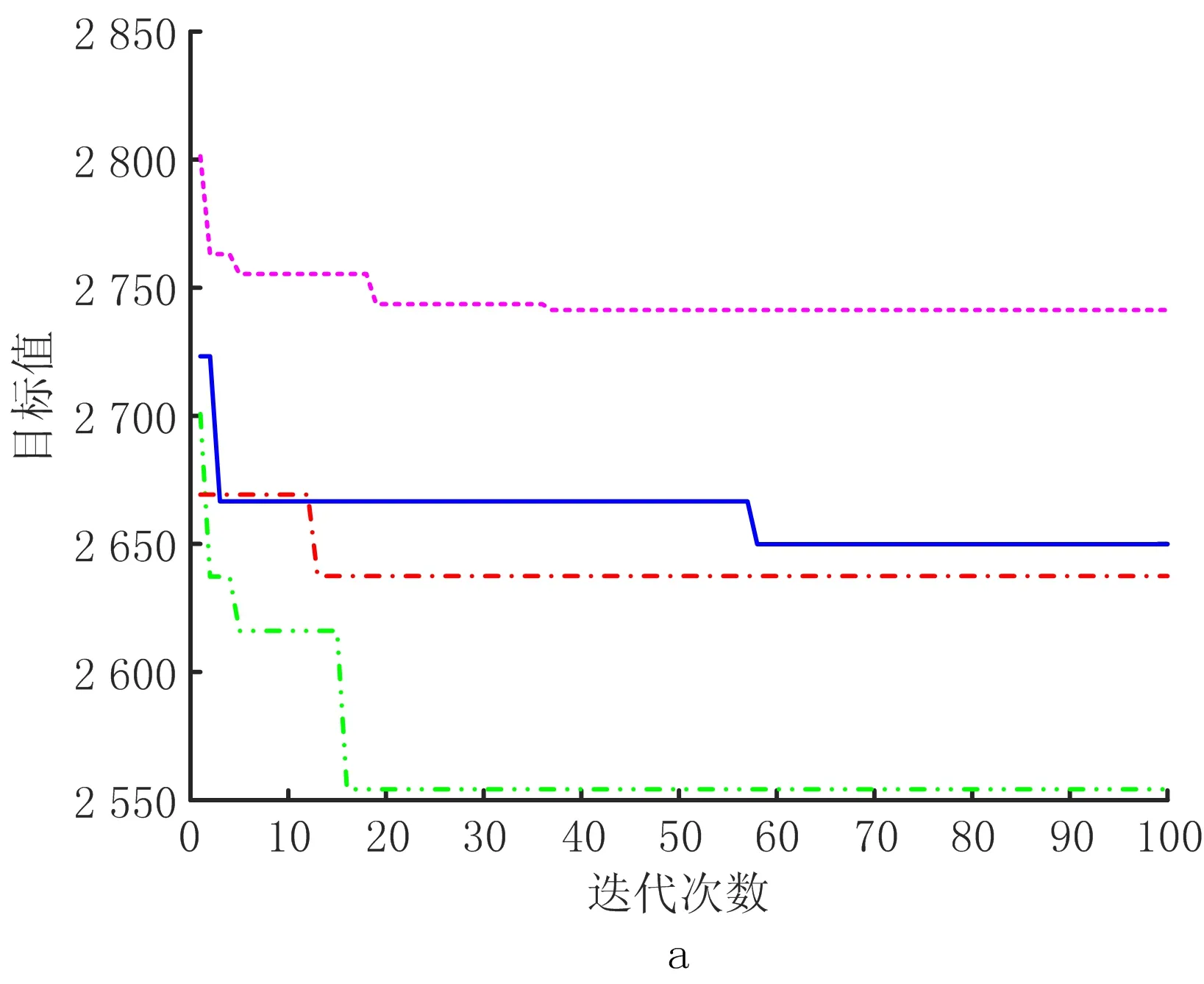
为了进一步展示几种算法性能的整体比较,本文利用4种不同算法在不同规模下进行对比,如图8所示。其中图8a~图8d分别表示在集装箱120、200、800、2 000个时的不同算法的收敛情况。从图中可以观察到HGACS的收敛时间随着规模的增大而增大的,收敛结果比其余算法要好。从图8c和图8d可以看出,大规模算例下,HGACS算法前期收敛速度比其他算法要好,最终分别在346代和351代收敛到最优解。这是因为在交叉操作时引入莱维飞行的更新策略,长短步长相结合的方式,使得算法向更好的方向搜索,同时采用自适应变异策略使得算法能够跳出局部最优解,所以该算法在求解时间和质量上都具有更优异的性能表现。而其他算法在大规模算例下,迭代后期过早收敛易陷入局部最优解。综上可知,本文所设计的算法求解小规模和大规模问题的结果都是比较优异的。

5 结束语
本文通过数值实验验证了所建立的模型能有效的解决U型自动化码头的集成调度优化问题,提出的算法能稳定地获得算例的近似最优解。两种调度策略对比表明,当任务规模较小时,AGV不等待外集卡的策略的结果较好,并且随着任务量的增多,两者的差值逐渐减小;当任务规模较大时,采用AGV等待外集卡一同装卸的策略结果较好,并且随着任务量的增多,两者的差值逐渐增大。该方法能够在合理的时间内获得有效调度策略和决策方案,符合U型自动化码头高效经济的发展需求。
然而自动化码头的作业优化问题涉及很多方面,是十分复杂的实际工程问题,本文对该问题进行了简化,对于不确定因素只是考虑了外集卡到达的不确定性,未来可以考虑其他不确定因素,如船舶到达时间的确定性,装卸设备故障等,还可以考虑AGV和外集卡的拥堵和冲突、外集卡预约系统、外集卡碳排放量等因素,也可以考虑U型自动化码头海铁联运的调度优化。

