基于LNN-DPC加权集成学习的转炉炼钢终点碳温软测量方法

熊 倩，刘 辉+，刘旭琛

(1.昆明理工大学 信息工程与自动化学院，云南 昆明 650500； 2.昆明理工大学 云南省人工智能重点实验室，云南 昆明 650500)

0 引言

转炉炼钢是以钢铁料、铁合金等金属材料和其他非金属料，依靠熔池中大量复杂的物理和化学反应产生的热量，完成炼钢的过程[1]。其关键在于实现对吹炼终点的控制，即在吹氧结束时，熔池中钢液的碳含量、各金属元素的含量和温度能同时达到出钢要求。因此，实现转炉终点碳温的准确预报，能有效缩短冶炼时间，减少原材料消耗，降低生产成本，并提高成品钢的品质。

目前，转炉终点碳温测量方法有人工经验法、副枪检测法、炉气分析法、火焰图像处理、光谱分析和生产过程数据的软测量方法[2]。其中，人工经验法受人为主观因素的影响生产效率较低。副枪检测和炉气分析由于设备本身的安装费用和维护成本过高，无法在中小型转炉企业中推广开来。随着智能检测技术的发展，基于火焰图像、光谱分析[3-8]、生产过程数据软测量实现终点碳温预报的方法成为研究热点。周木春等[9-10]采用支持向量机和基于模糊支持向量机的光辐射状态识别实现转炉终点判断，而火焰光谱图像的采集往往会受到环境因素及炉内烟气的影响，难以有效精确预测出终点碳温值。然而，对炉内尚不明确各原材料物理化学反应机理的生产过程，基于数据驱动的转炉炼钢生产过程数据软测量建模方法[11-15]着重考量生产过程数据输入变量与终点碳温之间的关系，能够保证出钢的品质。刘畅等[16]对实际的工业数据进行分析，运用基于事件驱动的策略，采用最小二乘支持向量机和改进粒子群算法构建预测模型提高模型的普适性，表明软测量方法运用于转炉炼钢生产过程是有效的。

在基于数据驱动的转炉炼钢生产过程数据软测量方法中，终点碳温的变化会受到熔池中投放的铁水、废钢、石灰石等原材料的影响，SHI等[17]在高炉相对稳定的条件下采集过程数据，利用主成分分析和偏最小二乘算法预测铁水中的硅含量。但熔池内各原材料的差异导致炉次样本的波动较大，单一模型无法有效预测出高炉铁水中的各元素含量。因此，有学者提出通过划分数据子集构建局部模型预测主导变量的方法，以提升模型预测精度和鲁棒性。孙茂伟等[18]通过正则化互信息特征排序指标实现特征扰动的方法，对Bagging算法训练样本重采样输入特征抽取来产生训练数据子集；ZHANG等[19]提出一种新的集成模式树方法来预测高炉铁水温度，证明了集成模型比单个模型有更好的精度和鲁棒性；LYU等[20]将机理建模与数据驱动软测量建模方法相结合，采用负相关学习对Bagging进行修剪以生成集成模型预测铁水温度，该方法提高了预测精度和集成效率。而对于转炉炼钢生产过程数据，采用传统集成学习数据采样方法对训练样本采样得到的数据子集生成的模型并没有体现集成学习“分而治之”的思想，在不同的子模型下会产生相同的预测结果以致子模型失去了多样性。FONTES等[21]采用模糊C均值聚类的方法划分数据子集，通过非线性自回归神经网络模型预测生产工业过程铁水的温度和硅含量，证明通过聚类算法划分数据子集构建局部模型的方法，有一定的优越性。

本文提出一种基于密度聚类的灰色关联度加权集成软测量建模方法。首先，采用t-分布随机邻域嵌入(t-distributed Stochastic Neighbor Embedding，t-SNE)可视化样本间的分布情况，通过样本密度度量策略，为密度峰值聚类算法提出一种新的局部最近邻截断距离的计算方式，使得样本的类间方差更大、类内方差更小，以更好地划分转炉炼钢生产过程数据得到局部样本子集。其次，通过构建局部子集与原始生产数据之间的映射关系，生成局部高斯过程回归模型，并在原始数据子集中通过对灰色关联分析定位得到的局部样本子集初始质心进行信息熵加权，以获得加权后的子集“质心”。最后，为了减少测试样本在选择模型时的计算复杂度，通过灰色关联分析评判高斯过程回归子模型与测试样本之间的关联程度，确定子模型与测试样本之间的关联度权重，选择更优的模型来构建集成模型，提出灰色关联分析加权的集成融合方式形成集成学习器输出碳温预测结果。通过转炉炼钢终点碳温预测的仿真实验表明本文所提方法具有良好的预测精度。

1 基于LNN-DPC加权集成学习的终点碳 温软测量方法

1.1 基于密度聚类的转炉炼钢生产过程数据子集 构建

在炼钢过程中，传感器会采集到众多的生产过程数据，这些数据通常都是不相关的高维数据，而距离度量公式在高维数据下一般会失效[22]。因此，采用降维的方法可以有效避免高维数据距离度量失效的问题，同时提高聚类算法的表现能力。

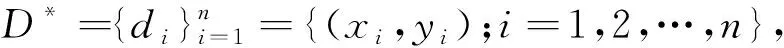
1.1.1 基于t-SNE的生产过程数据降维

t-SNE是一种高维数据降维方法，它通过数据之间的分布相似性将高维数据映射到低维空间，以可视化数据分布情况[23]。设生产过程数据在低维空间下映射的数据Dl={dli,i=1,2,…,n}，则di，dj对应生产过程数据点的条件概率为：

(1)

其中σi为中心在di的高斯方差，可以通过预先设定的复杂度因子执行二分搜索获得。在低维空间下，dli，dlj对应低维映射点的联合概率分布为：

(2)

根据条件概率的对称性获得高维数据和低维映射点的联合概率，t-SNE通过梯度下降算法最小化KL(kullback-Leibler)散度，达到最小化条件概率分布差异的目的，使得相似度较高的样本点在低维空间下的距离较近，相似度低的样本点在低维空间下的距离较远。

1.1.2 改进的密度峰值聚类算法

通过转炉炼钢生产过程数据t-SNE降维的分布情况，从数据样本间的紧密程度考量数据之间的相似程度，提出局部最近邻密度峰值聚类算法(Local Nearest Neighbour Density Peak Clustering, LNN-DPC)，来划分生产过程数据样本子集。

DPC[24-26]是一种基于密度聚类的方法，该方法能够直观地找到类簇的数量并进行高效聚类。对于数据集Dl，数据dli的局部密度

(3)

式中：distij为数据dli、dlj之间的距离;distc为数据的截断距离。

在原始DPC算法中，截断距离distc选取需要满足平均每个样本点的相邻个数为所有点的1%～2%的条件，但这只考虑了距离的全局信息，没有考虑到每个样本与剩余样本间的局部信息。因此，本文提出一种适应于生产过程数据样本子集划分新的确定截断距离的方法。根据近邻的思想，确定局部近邻(Local Nearest Neighbour，LNN)的截断距离，其定义如下：

每个样本距离distij的标准差为：

(4)

(5)

局部截断距离为：

(6)

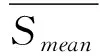
(7)

该算法把局部密度ρi和相对距离δi都相对较高的点作为类簇中心，为了方便寻找聚类中心的数量，可设置决策值γi=ρiδi，γi越大就越有可能是类簇中心，剩余数据点则分配至密度比它大且最近邻数据点所在簇。通过建立低维数据子集与原始数据的一一对应关系，获得原始生产过程输入数据下的样本子集R={r1,r2,…,rm}，m表示数据集的样本划分数量。

1.2 生产过程数据样本子集“质心”确定

灰色关联分析[27](Gray Correlation Analysis, GCA)通过参考序列与比较序列之间的相似程度来判断序列之间的关联程度。给定转炉炼钢生产过程数据样本子集X={xi;i=1,2,…,nm}。 其中，xi∈h，nm为每个子集的样本个数，h为特征变量的维度。设定每个样本都作为参考序列，其余样本为比较序列，设参考序列为x0={x0(1),x0(2),…,x0(h)}，根据GCA算法计算灰色关联系数：

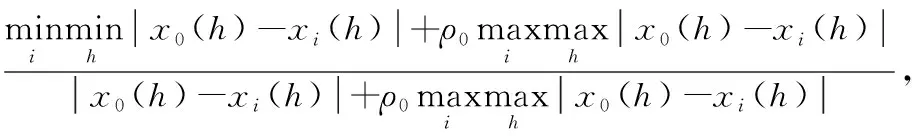
(8)

式中ρ0为分辨系数。计算参考序列与比较序列的关联度为：

(9)

根据上式，nm个样本生成的关联度矩阵为：

(10)

选择与所有数据关联最为密切的样本为最大关联序列，即子集的初始“质心”Z*。 然后，根据式(8)计算最大关联序列下各个特征变量的关联系数，得到各指标的关联系数矩阵:

(11)

为了得到客观的子集“质心”，引入信息熵加权[28]描述关联系数矩阵下每个特征变量的变异程度来修正指标，为特征变量赋予客观的权重。一般来说，特征变量的信息熵越小其变异程度越大，信息量越多，则分配的权重也越大;反之，信息熵越大特征变量的重要程度越低，权重越小。通过上式的关联系数矩阵，计算第h个特征变量下第i个样本的特征值比重为：

(12)

第h个特征变量的熵值为：

(13)

那么，关联系数矩阵中各个特征变量的权值：

(14)

最终得到加权的子集“质心”Zm=whZ*，表示有m个类的生产过程样本子集“质心”。

1.3 转炉炼钢生产过程数据加权集成软测量模型

1.3.1 基于高斯过程回归的碳温预报子模型构建

yi=f(xi)+ε,ε～N(0,σ2)。

(15)

式中：ε是均值为0、方差为σ2的高斯噪声;f(xi)是未知函数，且服从高斯分布。因此，Ym也服从均值为零的高斯分布为：

Ym～N(0,C(Xm,Xm)+σ2I)。

(16)

式中：C(Xm,Xm)为训练输入的协方差矩阵，I为单位矩阵。

对于测试输入样本x*的测试输入f(x*)和训练输出Ym的联合分布为：

(17)

则f(x*)的后验分布为：

f(f(x*)|Ym,Xm,x*)～N(μ(x*),σ(x*))，

(18)

f(x*)=μ(x*)=C(Xm,x*) (C(Xm,Xm)+σ2I)-1Ym。

(19)

均值和方差分别为：μ(x*)=C(Xm,x*)(C(Xm,Xm)+σ2I)-1Ym，σ(x*)=C(x*,x*)-C(Xm,x*)(C(Xm,Xm)+σ2I)-1CT(Xm,x*)，μ(x*)就是测试输入样本x*的碳温预测输出值，σ(x*)则为碳温预测输出值的方差。

关于核函数，采用平方指数协方差核函数则定义为：

(20)

式中：σf为信号标准偏差，σl为长度尺度。对于上述提到的参数，称为超参数，记作θ=[σf,σl,σ]，通过极大似然求取得到。

1.3.2 碳温预报子模型的选择和融合策略

建立GPR子模型其实就是假设空间根据给定的转炉炼钢生产过程数据建立模型空间的一个过程。然后，通过优化模型参数，找到与给定数据最为匹配的模型空间参数来确定模型。

因此，本文寻找最能代表整个数据子集的“质心”Zm，通过Zm与测试样本之间的关联程度来描述子模型与测试样本之间的联系，从而选择子模型进行集成加权。经生产过程数据子集集合R训练生成m个GPR模型记为M=[M1,M2,…,Mm]，选择更优的子模型生成集成模型可以为测试样本x*获得更好的碳温预测结果，提高集成学习器的表现性能。通过GCA准则分析测试样本x*与Zm之间关联程度，以碳温测试样本为参考序列，m个子集“质心”Zm为比较序列，得到x*的关联度集合Ω=[ω1,ω2,…,ωm]。 当ωm的值大于或等于V∈[min(ωm),max(ωm)]时，则保留其所对应的数据子集训练的GPR子模型，完成模型选择过程。

保留下来的子模型为Mnew=[M1,M2,…,Mα],α∈[1,m]，其对应的数据子集为Rnew={r1(x1,i,y1,i),r2(x2,i,y2,i),…,rα(xα,i,yα,i)},α∈[1,m],i=1,2,…,nm，则对应的关联度集合为Ωnew=[ω1,ω2,…,ωα],α∈[1,m]。 对于测试样本x*，在GPR子模型上的终点碳温输出结果为：

ypred,α=C(xα,i,x*)(C(xα,i,xα,i)+σ2I)-1yα,i。

(21)

式中：C(xα,i,xα,i)为训练输入的协方差矩阵，C(xα,i,x*)为测试样本与训练数据的协方差矩阵。GCA加权融合的终点碳温预测输出结果为：

(22)

2 基于转炉炼钢生产过程数据的加权集成 学习终点碳温软测量模型

转炉炼钢生产过程数据软测量建模具体操作流程如图1所示。

2.1 基于LNN-DPC的碳温预报子模型构建

转炉炼钢生产过程数据通常都是高维数据，由于密度峰值聚类算法的主要变量都是与距离度量相关，通过t-SNE将标准化后的原始数据样本降至二维空间下，避免了高维数据下采用距离度量失效问题，可以减少计算的复杂度。采用提出的改进峰值密度聚类算法(LNN-DPC)划分数据子集并建立与原始数据的一一对应关系，训练得到GPR子模型。

其中，采用LNN-DPC对生产过程数据样本集进行划分，其算法实现过程如下：

(1)对转炉炼钢生产过程数据进行预处理，通过t-SNE将D*映射至二维空间下；

(2)计算两两数据样本之间的距离值distij；

(3)通过每个样本的局部截断距离，计算全局截断距离distc；

(4)根据全局截断距离distc计算每个样本的局部密度ρi和相对距离δi；

(5)通过局部密度ρi和相对距离δi计算决策值γi，以样本点数量为横坐标，γi为纵坐标，绘制子集的数量决策图；

(6)利用决策图，将γi较大的值标记为子集中心以确定子集的数量；

(7)将剩余的点分配至与子集中心最近且密度较高样本点邻近的区域所在的子集中。

采用t-SNE对生产过程训练数据集降维，在低维空间下的数据分布如图2a和图2d所示，通过LNN-DPC划分生产过程数据的类簇个数决策图如图2b和图2e所示，最终子集划分结果如图2c和图2f所示。

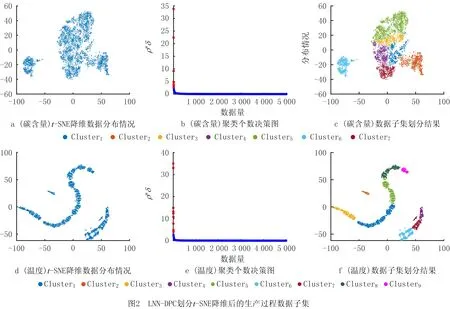
最终将碳含量生产过程数据划分为7个子集，温度数据划分为9个子集。根据原始数据样本子集训练GPR局部模型，从而获得一组具有多样性的GPR基学习器。

2.2 碳温预测子模型的选择集成融合策略

通过选择合适的GPR子模型来组成集成学习器是提高模型预测性能和泛化能力的关键一步。引入信息熵为GCA准则定位的子集“质心”特征变量加权获得较为客观的子集“质心”，利用GCA确定测试样本与子集“质心”的灰色关联度来选择GPR的子模型，即选择关联系数大于某一阈值V所对应的GPR子模型组成集成学习器，最后根据GCA加权集成融合策略得到最终的预测结果。

为了构建预测性能较好的集成学习器，需要选择与测试样本相关性较强的GPR子模型，因此本文通过评价基于信息熵加权的子集“质心”与测试样本的灰色关联系数，实现对GPR子模型的选择。实现方法具体如下：

(1)根据LNN-DPC获得低维数据子集并建立与原始生产过程数据之间的对应关系，得到高维数据下的数据子集集合R，训练生成GPR子模型；

(2)计算每一个子集中两两样本之间的灰色关联度形成关联度矩阵，找到最大关联序列，得到未加权的子集“质心”Z*；

(3)计算最大关联序列下各个特征变量的关联系数，通过信息熵确定Z*的权重；

(4)获得加权的子集“质心”Zm；

(5)计算测试样本和每一个子集“质心”的灰色关联系数；

(6)判断所有子集的灰色关联系数大于某一个阈值V所对应的训练模型及关联系数，这些模型就作为最终集成学习器的基模型；

(7)根据上述所得到的基模型和关联系数对基模型进行加权集成，得到加权集成学习器；

(8)输出碳温预测结果。

对测试样本x*，不同的GPR子模型会得到不同的预测值，而子模型的预测性能优劣决定了集成模型预测精度和泛化能力的好坏。通过GCA判断测试样本和子模型之间的关联程度，选择子模型进行加权集成融合，提升了集成学习器的预测性能。

2.3 集成软测量建模具体实施步骤

转炉炼钢生产过程数据样本聚类的加权集成软测量建模主要过程如图3所示。

其基本操作步骤如下：

(1)利用传感器获取转炉炼钢生产过程数据，经过数据清洗、特征选择得到样本数据集，将其分为训练样本和测试样本；

(2)训练样本经t-SNE降维，通过LNN-DPC划分为m子集；

(3)建立每个子集与原始数据样本之间的一一对应关系并训练GPR模型，获得m个GPR子模型的同时采用信息熵为GCA定位的每个子集“质心”加权；

(4)分析测试样本与每个子模型之间的关联程度，选择该测试样本下关联系数大于阈值V的子模型作为集成所需的基模型，基模型所对应的灰色关联系数为权值；

(5)通过选择的基模型和权值进行融合组成加权集成预测模型，将测试样本输入预测模型最终得到碳含量和温度的预测结果。

本文采用均方根误差RMSE、平均绝对百分比误差MAPE和预测精度PA评价预测模型性能，其计算方法如下：

(23)

(24)

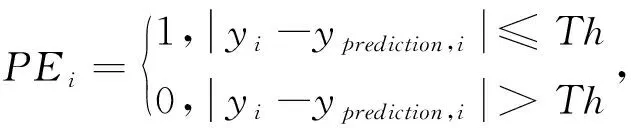
(25)

(26)

其中:Ntest为测试样本的数量;yprediction为预测值;PE表示预测误差在命中区间时即为命中，记为1，其他情况记为0;温度的预测误差范围Th=10℃，15℃，碳含量的预测误差范围Th=0.02%，0.03%。MAPE反应集成模型的优劣，该值越小表示集成模型越优;PA表示碳温在误差范围内的预测精度，该值越大表示该模型的预测性能越好。

3 转炉炼钢终点碳温预测模型仿真实验

3.1 实验数据及辅助变量特征

本文实验研究数据来源于某钢厂的实际炼钢生产过程数据。转炉炼钢终点控制的关键是实现对碳含量和温度的预报，但在转炉炼钢生产过程中通过传感器获得的数据有装入铁水量、装入生铁量、装入废钢量、铁水C、兑铁时长、吹氧量、枪位、氧压等126维。通过特征选择的方式，选择影响出钢时碳含量和温度的关键特征变量作为辅助变量，主导变量就是碳含量和温度。最终，分别选取6个特征作为辅助变量，其关键变量如表1所示。

表1 转炉炼钢生产过程数据变量表

在实验过程中，生产过程数据实验样本总共有5 500组，训练样本集5 000组，测试样本500组。表1中所示的部分特征名称中所含数字表示不同时刻点传感器对该特征进行测量的次数[11]。一般情况下，出钢温度在1 590～1 680℃范围内，以1 600℃为例，10～15℃的相对误差范围在0.63%～0.94%之间，根据不同品质的钢的出钢要求有不同的误差允许范围。

3.2 转炉炼钢终点碳温预测实验及结果分析

利用转炉炼钢生产过程数据验证基于LNN-DPC样本聚类的软测量GCA模型选择加权集成建模方法的有效性，其中通过比较GPR全局建模、Bagging(GPR)、随机森林(Random Forest,RF)、梯度回归树模型(Gradient Boosted Regression Trees, GBRT)、Adaboost(GPR)和K-means聚类、层次聚类(Hierarchical Clustering, HC)、高斯混合模型(Gaussian Mixture Model Clustering, GMM)、模糊C聚类(Fuzzy C Clustering，FC)、DPC的方法验证LNN-DPC的有效性,聚类算法都是对GPR子模型进行集成；通过比较平均(Simple Average, SA)集成融合策略验证GCA加权平均(GCA Weighted Average, GCAWA)集成融合策略的有效性。实验结果数据表现如下，表2呈现了不同建模方法下温度和碳含量的预测性能指标，图4～图7分别是碳含量和温度的预测结果图。

表2 不同建模法预测碳含量和温度性能指标

续表2

从表2的实验结果可以看出，基于LNN-DPC样本聚类划分数据子集来构建GCA加权集成软测量模型的方法在转炉炼钢生产过程数据上的表现更优，说明该方法可以很好地通过生成样本的多样性从而构建子模型的多样性以保证集成模型泛化性能的同时提高预测精度。在转炉炼钢生产过程数据中基于样本聚类的方式划分数据子集的建模方法优于全局建模和传统的集成学习软测量模型，说明这种划分数据样本的方法在转炉炼钢生产过程数据上能够构建出更加多样性的子模型，从而提升集成模型的泛化能力。对于集成融合过程，通过GCA选择GPR子模型进行集成，去除部分对于测试样本来说预测效果不佳的子模型，使得构建的GCA加权集成学习器对测试集有更好的预测性能。

图5d和图7d分别是本文所提方法的碳含量、温度预测结果图。从两图中可以看出，该预测模型对终点碳温都有很好的预测效果，从RMSE上来看，本文方法预测结果表现更好；从MAPE来看，本文方法构建的模型相对于其他方法也更合理。

综上所述，说明LNN-DPC算法在生成转炉炼钢生产过程数据子集上有一定优越性，GCA准则选择子模型的同时进行集成学习器子模型加权的方法也有较理想的终点碳温预测精度。

4 结束语

本文针对转炉炼钢生产过程原材料品质差异导致的过程数据波动性较大，造成全局软测量模型以及传统的集成学习模型无法精确描述转炉炼钢生产过程的实际工况的问题，提出一种基于LNN-DPC的软测量GCA加权集成建模方法具体总结如下：

(1)通过LNN-DPC划分数据子集，保障了数据子集多样性的同时也保证了构建子模型的多样性。

(2)采用GCA准则选择GPR子模型并进行加权融合的方式减少了冗余的子模型，以选择更优的模型进行集成从而提高预测精度，得到更好泛化性能的预测模型。

通过对转炉炼钢生产过程数据的实验仿真，验证了该方法可以有效地解决生产过程数据中终点碳温预报的问题，相比于全局建模和传统的集成学习方法也有更好的预测性能，说明基于样本聚类的集成学习软测量建模方法为生产过程数据终点碳温预报的研究提供了更好的研究方向，而且本论文的方法也为转炉炼钢过程生产提供了合理的建模过程。随着转炉炼钢生产过程的工况不断变动的情况，如何使得集成软测量模型自适应的更新，并能够不断地适应生产过程变化的情况将是下一步的研究方向。