着手特殊角度 一题多解
西华师范大学数学与信息学院
彭 亚 高 明
1 如何实现一题多解
一题多解,是指从不同的视角出发来分析题目,用多种方法来解题.它不仅能促进学生对题目本质的理解,还能发展他们的思维,更能激发他们解题的兴趣,使数学解题教学充满趣味性,数学课堂氛围也变得活泼.本文中以一道常见的解三角形题目为例,分析题目的多种解法,展现解题过程,促进学生对一题多解的进一步认知.
解题的本质就是对题进行变换和化归.要想实现一题多解,首先要拆解题目,明白题目具有的信息特征.比如数量、结构、关系、图形等特征,不同的特征会带给我们不同的解题视角.其次,选择解题的策略.解题策略包括变、换、构、拆、凑,这也是一题多解的角度,不同的角度拟定不同的解题计划.接着,根据解题计划逐步实施.最后反思解题过程能否继续优化拓展.
2 典例分析
例在△ABC中,角A,B,C所对应的边分别为a,b,c,若角A,B,C的大小成等比数列,并且b2-a2=ac,求角B的大小.
思维视角一:根据余弦定理解题.
分析:由题中的条件b2-a2=ac出发,观察该式的结构,联想到余弦定理,二者联合可以得到角A与角C的关系,结合题中条件角A,B,C成等比数列,求出角B.
解:由余弦定理,可得b2=a2+c2-2accosB.
又因为b2-a2=ac,所以c2-2accosB=ac.
即a=c-2acosB.
由正弦定理,得
sinA=sinC-2sinAcosB.
即sinA=sinC-[sin(A+B)+sin(A-B)].
即sinA=sin(B-A).
由于A,B∈(0,π),所以A=B-A,即B=2A.
又因为角A,B,C成等比数列,所以B2=AC.
即C=4A.
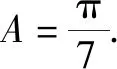
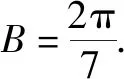
点评:这道题是典型的解三角形问题.常规思路是分析题中的已知条件,观察各边和各个角的关系,根据题中的边角关系来选择解题方法.解题的大方向会涉及到用正弦定理和余弦定理来求解.本题根据边和角的关系选择余弦定理,结合三角成等比数列,求解得到角B.这个方法是最常见的解三个角形方法,是大多数同学容易想到的.
思维视角二:根据托勒密定理解题.
分析:可以从几何角度将式子b2-a2=ac变成b2=a·a+a·c.由此根据平面几何中的托勒密定理来求解此题.托勒密定理的内容,即圆的内接四边形两组对边乘积的和等于两条对角线的乘积.那么,我们构造一个圆的内接四边形,作出对角线,便可得出各个角之间的关系.
解:由b2-a2=ac,得b2=a·a+a·c.构造一个圆O及其内接四边形ABCD,使AB=c,CD=a,BC=AD=a,BD=AC=b,如图1所示.
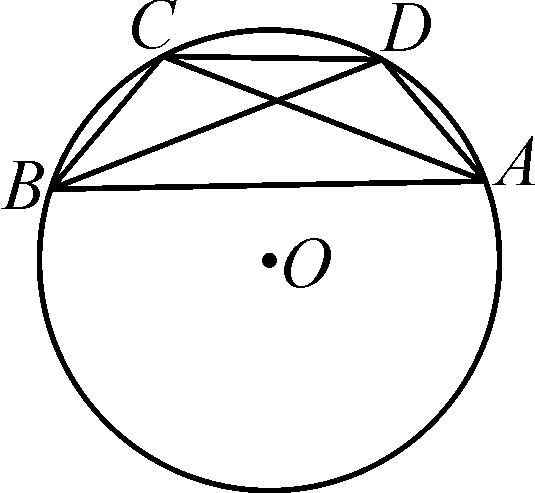
图1
即四边形ABCD满足托勒密定理:
AC·BD=BC·AD+AB·CD.
由于BC=CD=AD=a,故
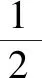
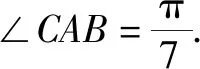
点评:这种解法是从变换b2-a2=ac的角度出发,观察式子的特征联想到托勒密定理,进而构造几何图形来求解.这种视角将代数式与几何图形联系在一起,即代数问题几何化,是一题多解的一种独特视角.
思维视角三:根据相交弦定理解题.
分析:相交弦定理说的是,圆内的两条相交弦,被交点分成的两条线段长度的积相等.所以将b2-a2=ac看成(b-a)(b+a)=ac,即将线段a,b,c构造成满足相交弦定理的图形,再从图形中寻找各个角之间的数量关系,结合三个角成等比数列的条件进行求解.
解:如图2所示,作一个半径为b的圆C,直径MN过圆心C,取线段MN上的点B,使BC=a,过点B作弦PA,使PB=a,BA=c,连结PC,AC.则BN=a+b,BM=b-a,BP=a,BA=c,满足相交弦定理.
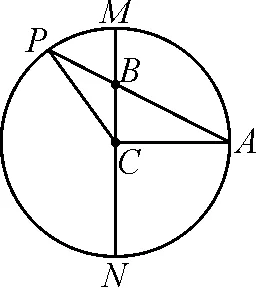
图2
因为PB=PC,所以∠BPC=∠BCP.
因为CP=CA,所以∠BPC=∠A.
所以∠ABC=∠BPC+∠BCP=2A.
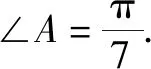
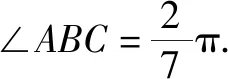
点评:将b2-a2=ac看成(b-a)(b+a)=ac,即对式子进行变换,并且联想到相交弦定理,构造图形找到角与角的数量关系,降低了解题的难度.
3 总结
一题多解的解题教学是非常有必要的.如何系统地对学生进行一题多解教学,如何培养学生从多视角观察分析问题,是当下数学教育工作者需要思考的问题.一题多解不仅有益于思维的拓展,更有利于展现数学之美,是对学生进行数学美育渗透的一种重要渠道.

