学案模式 逐层递进
——“余弦定理、正弦定理”教学设计
江苏省海安高级中学
杨 玫
余弦定理、正弦定理是新人教A版普通高中数学必修第二册第六章“平面向量及其应用”第4节内容,作为平面向量的一大应用,可以与平面几何、三角函数、平面向量等相关知识交汇、融合,同时也为解决三角形问题提供了基本且重要的工具.
在实际教学过程中,以学案形式,对“余弦定理、正弦定理”部分做了如下对应的教学设计.
1 提前预习
1.1 读一读——学习目标
(1)从特殊的直角三角形入手,借助向量运算,探索任意三角形边长与角度的关系,通过平面向量的应用来分析与推导余弦定理、正弦定理,进而掌握余弦定理与正弦定理,并能利用这两个定理解决一些简单的三角形度量问题;
(2)掌握余弦定理、正弦定理的推导,并运用定理解决一些与三角形有关的数学问题.
1.2 看一看——重点难点
重点:
(1)理解并掌握平面向量法推导余弦定理的过程,理解并掌握余弦定理及其相关应用;
(2)理解并掌握平面向量法推导正弦定理的过程,理解并掌握正弦定理及其相关应用.
难点:
(1)理解与掌握余弦定理的推导过程与相关应用;
(2)理解与掌握正弦定理的推导过程与相关应用.
1.3 填一填——基础知识
1.3.1 余弦定理
三角形中任何一边的平方,等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍,即a2=______,b2=______,c2=______.
1.3.2 正弦定理
在一个三角形中,各边和它所对角的正弦的比相等,即______=______=______=______.
正弦定理揭示任意三角形中各边与对应角的内在的数量关系,即任意三角形中三条边与对应角的正弦的比值之间的关系式,它是三角形中最基本的数量关系式.
2 课堂教学
2.1 探一探——定理推导
(1)余弦定理的推导(课本第42页对应部分).
(2)正弦定理的推导(课本第46页对应部分).
此处借助平面向量的应用,结合教师的分析与讲解,通过PPT加以展示证明过程.同时,适当引导学生根据所学的知识,探究证明余弦定理与正弦定理的其他方法与应用.教师可以根据班级学生的不同情况加以适当安排.
2.2 学一学——方法讲解
(1)余弦定理是勾股定理的推广.当a2+b2=c2时,∠C=90°;当a2+b2>c2时,∠C<90°;当a2+b2
(2)利用余弦定理可以解决两类斜三角形问题:
①已知三角形的三边求各对应的内角;
②已知三角形的两边和这两边的夹角,求第三边和其它两个角.
由三角形全等的判定定理知,以上两类斜三角形都是确定的,所以对应问题的解也是唯一的.
(3)正弦定理的变形形式:
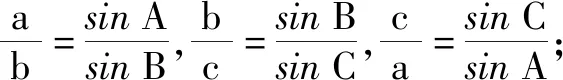
②a=2RsinA,b=2RsinB,c=2RsinC;
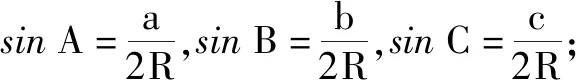
④a∶b∶c=sinA∶sinB∶sinC;
⑤asinB=bsinA,bsinC=csinB,asinC=csinA.
利用上述不同形式可进行三角形的边、角及外接圆半径之间的互化.
(4)正弦定理主要用来解决两类常见问题:
①已知三角形的两角与一边,解三角形;
②已知三角形的两边与其中一边的对角.
特别注意,利用正弦定理解决有关“已知两边与其中一边的对角”的斜三角形问题时,要对三角形解的不同情况进行分类讨论:有两解,有一解,无解.具体情况如下:
当A为锐角时,如图1.
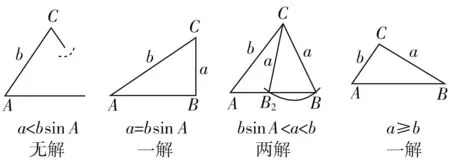
图1
当A为钝角时,如图2.
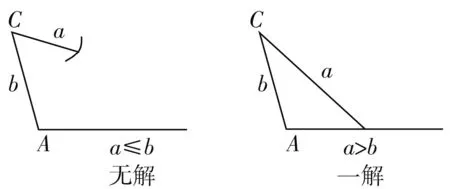
图2
(5)余弦定理和正弦定理的区别与联系:
①区别:余弦定理主要是三角形的其中一个内角的余弦值与三条边的关系,而正弦定理主要借助边的比和对应角正弦值的比互化来建立关系.
②联系:它们之间可以互推.
通过平面向量法来推导余弦定理与正弦定理时,利用余弦定理可以证明正弦定理,同样利用正弦定理也可以证明余弦定理.而破解相关的“已知两边与其中一边的对角”的斜三角形问题,一般通过正弦定理来解决,也可以借助余弦定理建立方程来巧妙解决.
(6)注意分类讨论:利用正弦定理解决相关的“已知两边与其中一边的对角”的斜三角形问题时,要通过分类讨论来处理,同时利用平面几何作图直观分析或“三角形中,大边对大角”等来合理推理.
注意隐含条件:利用余弦定理或正弦定理解决任意三角形问题时,要注意三角形自身隐含的条件,这里包含三角形的内角和定理及隐含的A,B,C均为正角等.
2.3 讲一讲——典例剖析
基本题型1:余弦定理的应用.
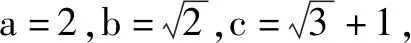
分析:已知三角形的三边,可以利用余弦定理的变形公式解决.注意求解过程中,充分利用三角形内角和定理加以简化运算.
解析:由余弦定理,得
因为0° 又由余弦定理,得 因为0° 由A+B+C=180°,可得C=180°-45°-30°=105°. 利用余弦定理求解有关三角形的内角问题时,往往会用到余弦定理的变形形式.其实,余弦定理的每一个等式都包含三角形六要素中的四个不同的量,它们分别是三角形的三条边和一个角.在余弦定理的每一个等式中,已知三个量便可求出第四个量. 基本题型2:正弦定理的应用. 分析:已知三角形的任意两角与一边,求解其他两边和另一角时,一般先由三角形的内角和定理,计算出三角形的另一角,再由正弦定理来计算出另外两边. 解析:由A+B+C=180°,可得C=180°-105°-45°=30°. (5)若三角形三边长的比为5∶7∶8,则它的最大角和最小角的和是______.(答案:120°.) (6)在△ABC中,a,b,c分别是角A,B,C所对的边,若(a+b+c)(sinA+sinB-sinC)=3asinB,求角C的大小.(答案:60°.) (8)已知△ABC的三个内角A,B,C的对边分别为a,b,c,若2b=a+c,且2cos 2B-8cosB+5=0,求角B的大小,并判断△ABC的形状.(答案:B=60°;等边三角形.) 通过以上课前预习、课堂教学、课堂练习的设计,以学案的形式展示余弦定理、正弦定理的推导过程、方法讲解、典例剖析,并通过随堂演练加以巩固.在实际教学过程中,学案式的教学设计也是一种基本教学设计形式,对学生知识的理解与掌握大有益处.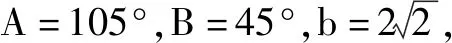
3 课堂练习
3.1 练一练——随堂演练
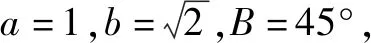
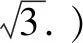
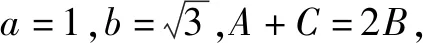

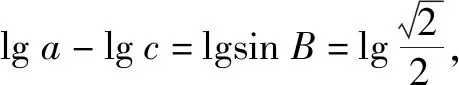
4 设计意图

