组合-混合梁结合段传力机理研究

董梅，赵灿晖，张永明，张育智，舒本安，刘志文

（1.佛山市交通投资集团有限公司，广东 佛山 528300；2.西南交通大学，四川 成都 610000；3.佛山市建盈发展有限公司，广东 佛山 528300；4.佛山市交通科技有限公司，广东 佛山 528300）

混合梁斜拉桥因具有受力明确、施工快捷等特点，近年来在国内大跨径斜拉桥中被广泛应用［1-3］。钢混结合段作为混合梁斜拉桥主梁中钢梁与混凝土梁的关键连接节段，因构造复杂且传递荷载大，其力学行为受到国内外学者的广泛关注。钢混结合段的研究重点：①荷载分配或传递路径（即钢混结合段中承压板与剪力连接件所传递荷载占总荷载的比例）；②钢混结合段中剪力钉、PBL等连接件的剪切刚度、疲劳性能等力学性能。黄彩萍等人［4］以武汉二七长江大桥为研究对象，分析表明荷载分配与剪力钉剪切刚度密切相关。李小珍等人［5］通过厦门马新大桥的缩尺试验，得到承压板与PBL剪力件所传递荷载各占50%。姚亚东等人［6］以甬江特大桥为原型，制作了缩尺比为1∶5的全截面模型进行试验研究和有限元分析，发现承压板对结构轴向力的传递有重分配作用。HE等人［7］以UHPC灌浆的钢混结合段为研究对象，通过试验研究发现，承压板承受总荷载的65%，其余35%由剪力件承担。针对剪力连接件的研究，黄翔等人［8］采用推出试验方法，得出了钢混结合段中PBL剪力件的极限承载力和抗剪刚度计算公式。周阳等人［9］设计并制作了甬江特大桥结合段中典型钢格室的足尺模型，对剪力钉和PBL剪力件群进行了疲劳荷载试验，剪力栓钉与PBL剪力件的配合使用，提高了结构的安全储备与抗疲劳性能。

组合梁是近年来桥梁设计的热点［10-12］，其截面中的混凝土桥面板面积较大，对截面的轴向刚度及抗弯刚度均有较大贡献，当组合梁用于结合段时，由于混凝土桥面板的存在，导致轴向力在截面上的分布规律、结合段内荷载传递机理与常规的钢-混凝土结合段有较大差异。为研究组合-混合梁结合段的传力机理，本研究拟以主跨为580 m富龙西江大桥为例，对中腹板区域进行1∶2缩尺模型试验，并采用Abaqus软件建立有限元模型，研究组合-混合梁截面各参数对结合段轴向传力路径的影响规律，以期为该类桥型结合段的设计提供参考。

1 模型试验

1.1 模型设计

富龙西江大桥主跨为580 m，主梁宽为41.4 m，主跨侧采用组合钢箱梁，边跨侧采用混凝土箱梁，结合段设置于辅助墩上，如图1所示。以该桥组合梁-混凝土梁结合段为例，选取主梁横断面中受力最显著的中腹板区域进行1∶2缩尺模型试验，如图2（a）所示。模型主体由组合梁、结合段和混凝土箱梁组成，对应的长度分别为1.30、1.07和2.50 m。

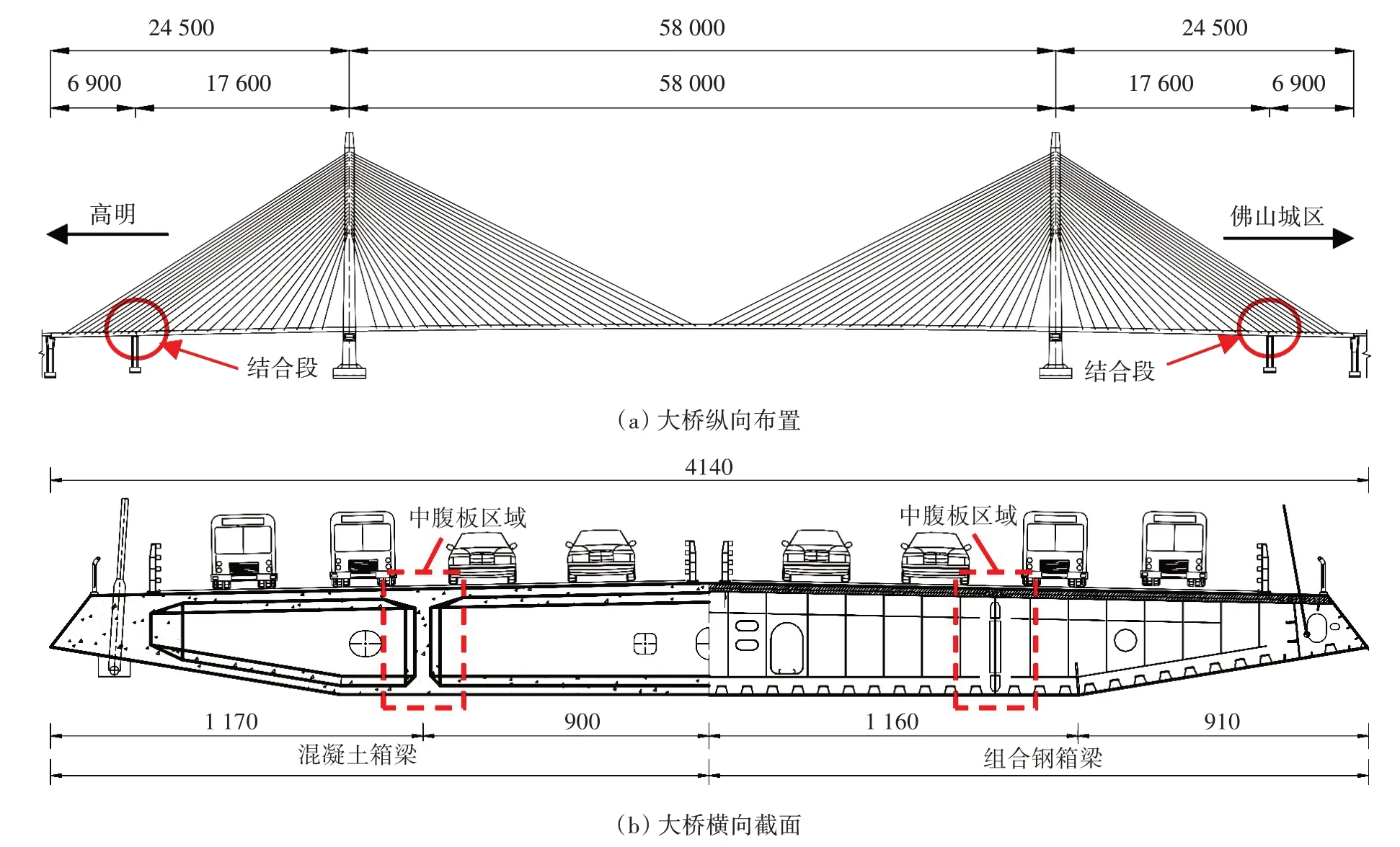
图1 富龙西江大桥钢混结合段布置（单位：cm）Fig.1 The layout of steel-concrete joint section of the Fulong Xijiang Bridge（unit：cm）

横断面尺寸为1.85 m×1.67 m，其中，组合梁截面内桥面板厚度为0.125 m，如图2（b）所示。板内分两层，共设置36根Φ12的HRB400纵向钢筋，钢梁顶、底板厚度为10 mm，腹板、顶板加劲与底板U肋为8 mm，底板加劲为12 mm，钢材为Q345。结合段与组合梁交界面上设有厚30 mm的承压钢板，组合梁各板件经承压板伸入结合段内，利用PBL剪力件和剪力栓钉与结合段混凝土相连，剪力件的布置如图2（d）、（e）所示。混凝土梁截面为工字型，其端部与加载锚座相连。

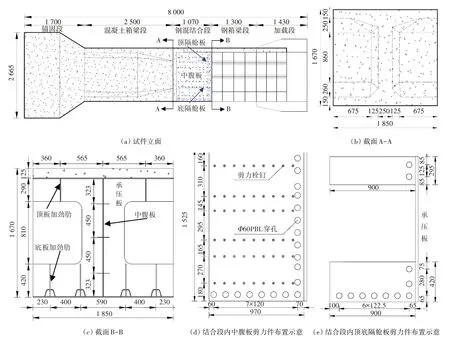
图2 模型结构布置图（单位：mm）Fig.2 The layout diagram of model structure（unit：mm）

1.2 加载方案

模型采用两组水平千斤顶进行加载，如图3所示。加载端截面上部布设2台250 t千斤顶，下部布设2台200 t千斤顶，利用锚座中预埋预应力钢绞线施加荷载。各千斤顶同步加载，各级荷载值如图4所示。最终结合段内总轴力为4 800 kN，总弯矩为2 500 kN·m，该荷载对应实桥中最不利轴力工况。

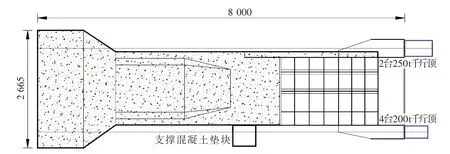
图3 加载示意（单位：mm）Fig.3 Loading schematic（Unit：mm）

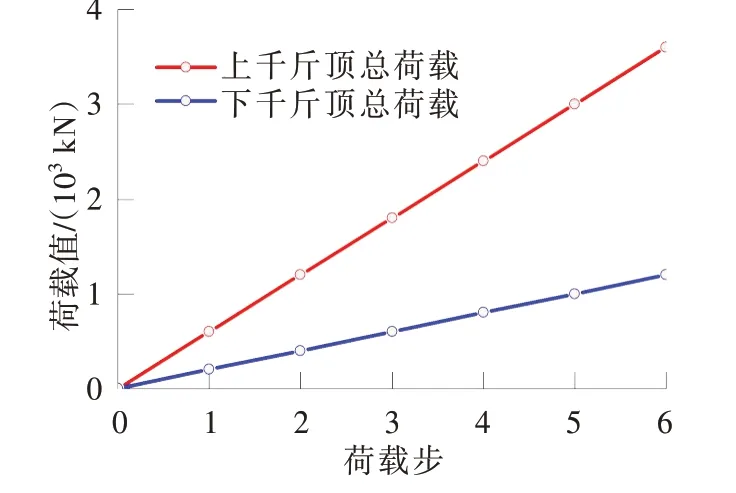
图4 加载步骤Fig.4 Loading procedure

1.3 应变测试方案

模型测点布置分为组合梁、结合段埋入区两个部分，如图5（a）所示。中腹板沿高度方向共设置9行轴向应变测点。结合段埋入区1列，组合梁内1列，编号分别为M1-1至M1-9、M2-1至M2-9。底钢板沿截面宽度方向设置4行轴向应变测点，组合梁内1列，结合段埋入区1列，编号分别为D1-1至D1-4、D2-1至D2-4，如图5（b）所示。顶钢板与底钢板测点布置相似，编号为T1-1至T1-4、T2-1至T2-4，如图5（c）所示。结合段埋入区的顶、底隔舱板上分别布置了3行1列、3行1列的轴向应变测点，对应的编号为TC1-1至TC1-3以及BC1-1至BC1-3，如图5（d）所示。桥面板内对应承压板的位置设置3个钢筋应变测点，编号为R1至R3，如图5（e）所示。

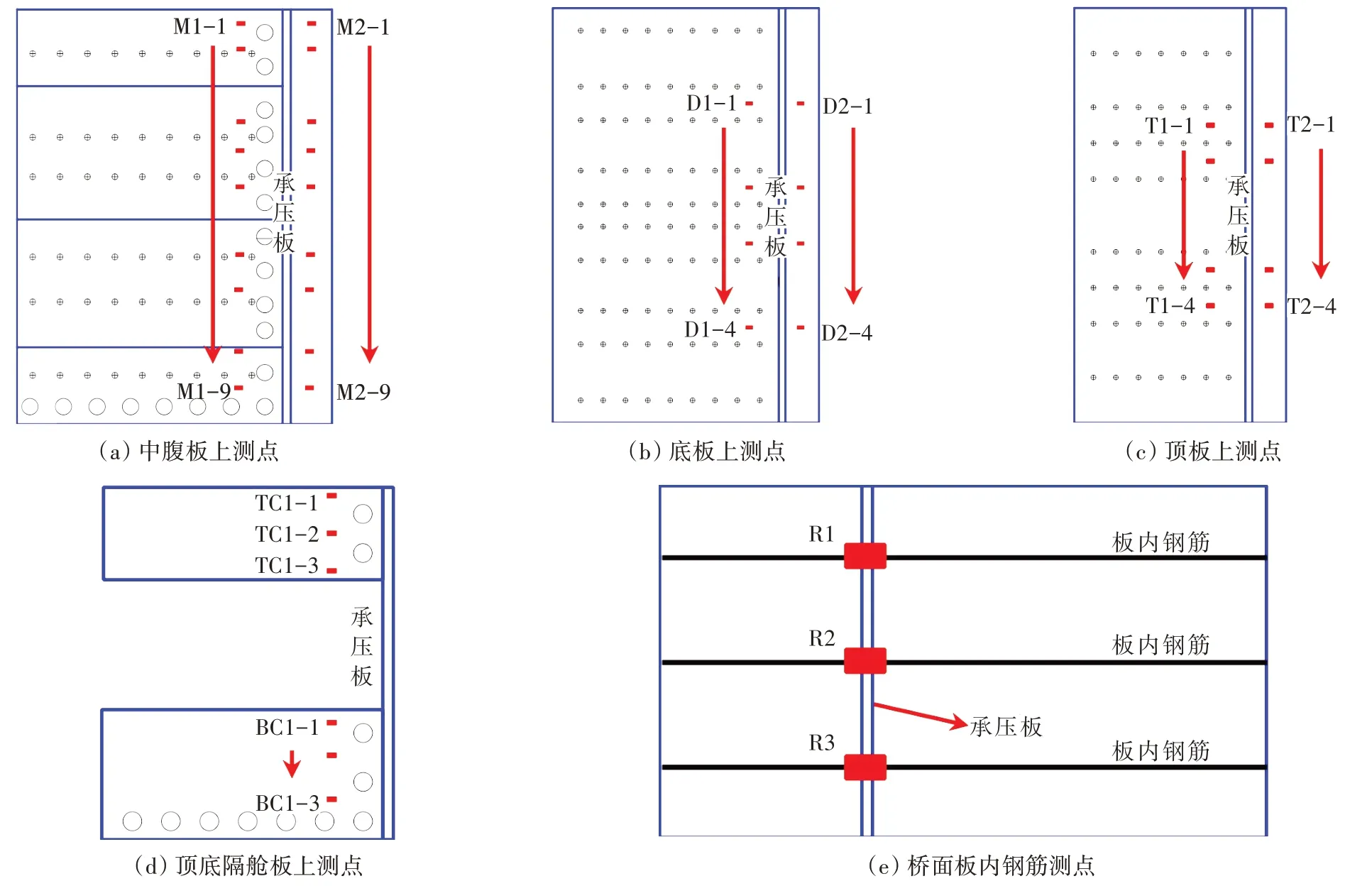
图5 应变测点布置Fig.5 The layout diagram of strain measuring points

2 试验结果

组合梁区域内腹板不同高度处的轴向应变如图6（a）所示。从图6（a）可以看出，各点应变随荷载增大呈线性增长，并且在轴压力+正弯矩组合作用下压应变从上到下呈依次减小的分布形式，最大应变值为-343με。组合梁内顶板整体截面均匀受压，平均压应变为-275με，组合梁内底板受压也较为均匀，但压应变较顶板小，平均压应变为-50με。

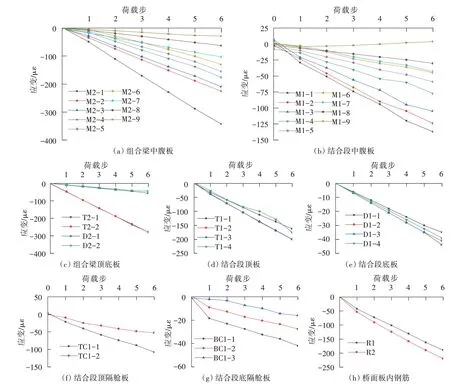
图6 应变测试结果Fig.6 Test results of strain

结合段内各钢板件在各荷载级下的中腹板上各测点的应变测试结果如图6（b）所示，其应变分布规律与组合梁区域测点相似，但同一荷载下的应变值较组合梁区域测点小，最大压应变为-141με。结合段内顶板与底板中测点测试结果如图6（d）和图6（e）所示，顶板与底板中各测点与承压板的距离一致，因此应变值相近。与顶钢板相连的顶隔舱板受压，如图6（f）所示。压应变达到-108με。底隔舱板全截面受压，压应变从上至下呈递减趋势，与底钢板相连处压应变最小为-16με，如图6（g）所示。桥面板内钢筋测点的应变结果如图6（h）所示，最大压应变达到-220με，测点TC1-3与R3受到破坏，无读数。

从图6还可以看出，承压板两侧的结合段截面和组合梁截面上同名板件具有相同的应变分布规律和不同应变大小，因此截面内力发生了重分布。承压板截面的受力构件包括：桥面板、承压板、各类钢板（中腹板、顶钢板、底钢板、顶隔舱板及底隔舱板）和结合段混凝土，该截面轴力传递的途径有3种：①桥面板自身传递；②承压板面压传递给结合段混凝土；③结合段内各纵向钢板通过剪力件群传递至结合段混凝土。

3 有限元计算及验证

为分析结合段的传力机理，采用Abaqus软件建立结合段全截面有限元模型，如图7所示。桥面板与混凝土箱梁均采用C3D8R实体单元，钢箱梁则采用S4R壳单元进行模拟。结合段中设置剪切弹簧，模拟剪力钉与PBL剪力件；桥面板内埋入Truss单元，模拟纵向钢筋。考虑承压板与结合段内结合段混凝土的接触效应，混凝土取规范［13］中C60混凝土的本构曲线，弹性模量为36.0 GPa，钢材料弹性模量取200 GPa，剪力钉与PBL剪力件的剪切刚度分别为575 kN/mm［14］与682 kN/mm［15］。

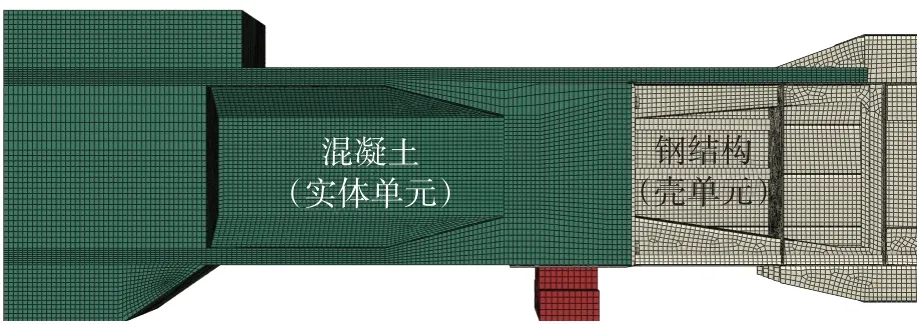
图7 有限元模型Fig.7 Finite element model

有限元计算结果与试验实测值的对比如图8所示。从图8可以看出，有限元计算结果与实测应变吻合良好，表明可以利用有限元计算结果对结合段的受力特征及传力路径进行分析。

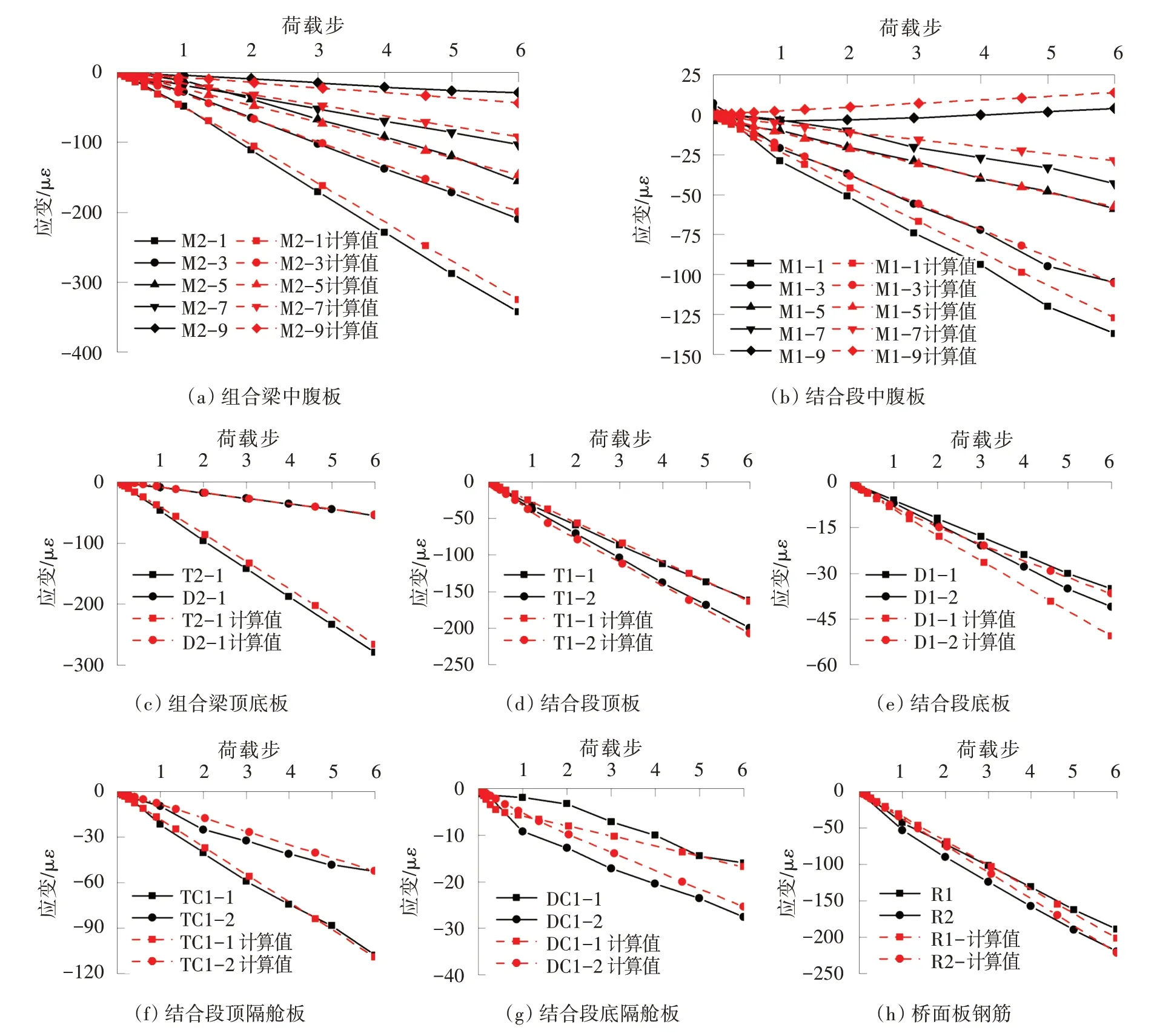
图8 有限元结果与试验结果对比Fig.8 Results comparison of finite element and test

根据试验中的三种轴力传递方式，为计算结合段各部分所传轴向力准确数值，利用有限元模型取多个截面如图9（a）所示。通过节点力积分的方式得到各部分传递的轴力及其占比，计算结果如图9（b）所示。从图9可以看出，C0截面处承压板所传递的轴力荷载占总轴力的32.2%，桥面板传递的轴力占总轴力的45.0%，剪力连接件传递给混凝土梁的轴力占比为22.8%。随着截面与承压板距离的增大，混凝土中的轴力持续增大，这是因为由剪力连接件传递给混凝土的轴向力持续增大，在C4截面处，混凝土承受的轴力占比达到56.2%，桥面板的轴力占比为38.5%，由于组合梁钢顶板在C3截面与C4截面间结束，C4截面上剪力连接件的合计轴力占比仅为5.3%。在整个传力过程中，各类钢板承受的轴力及桥面板中的部分轴力通过剪力件群逐渐传给结合段混凝土，桥面板中剩余轴力则由桥面板与混凝土箱梁的结合面直接传递给混凝土箱梁。

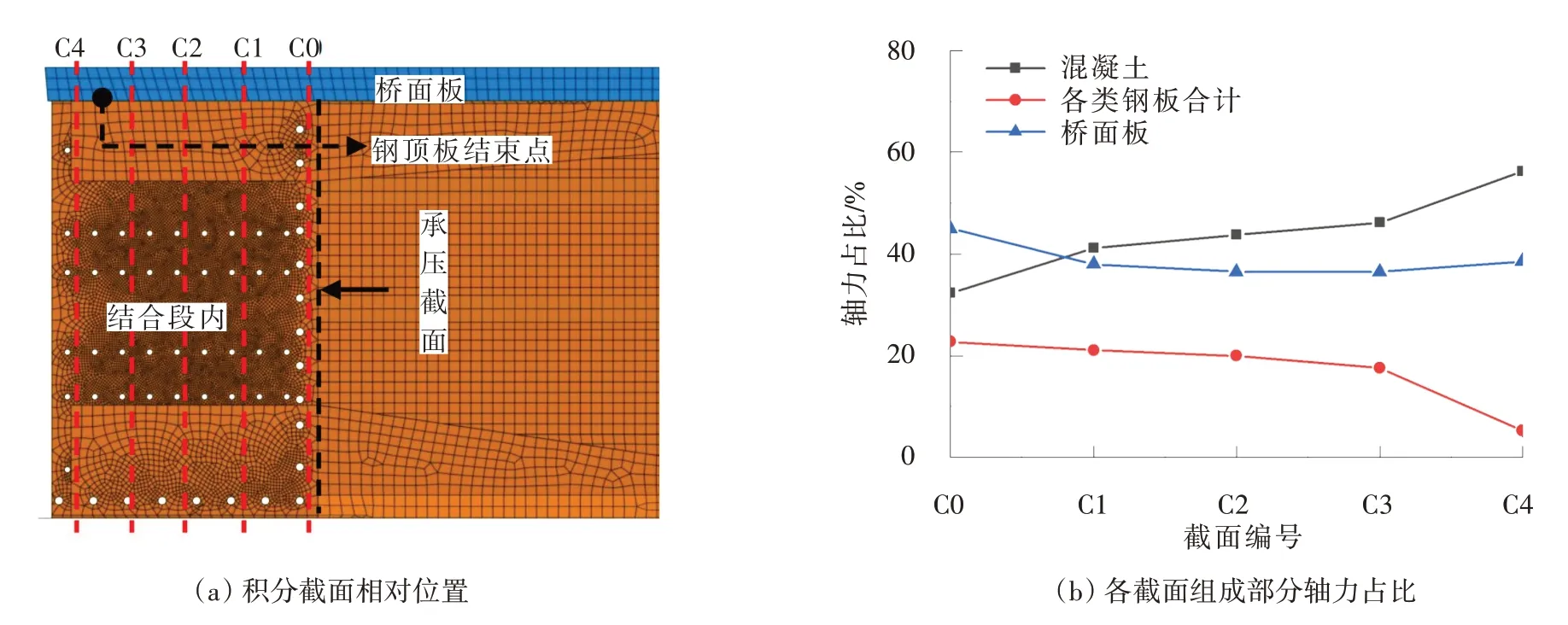
图9 组合梁-混合梁结合段轴力传递机理Fig.9 Axial force transmission mechanism of composite beam-concrete joint section

4 参数分析

为分析各种设计参数对组合-混合梁结合段轴力传递路径的影响规律，针对组合梁-混凝土梁结合段的桥面板厚度、承压板厚度、钢板（中腹板、顶底板、顶底隔舱板）厚度及剪力连接件刚度对结合段轴向力传递路径的影响进行了研究，各参数变化见表1。其中，Z1为原型，Z8的剪力键总刚度为Z1的一半。

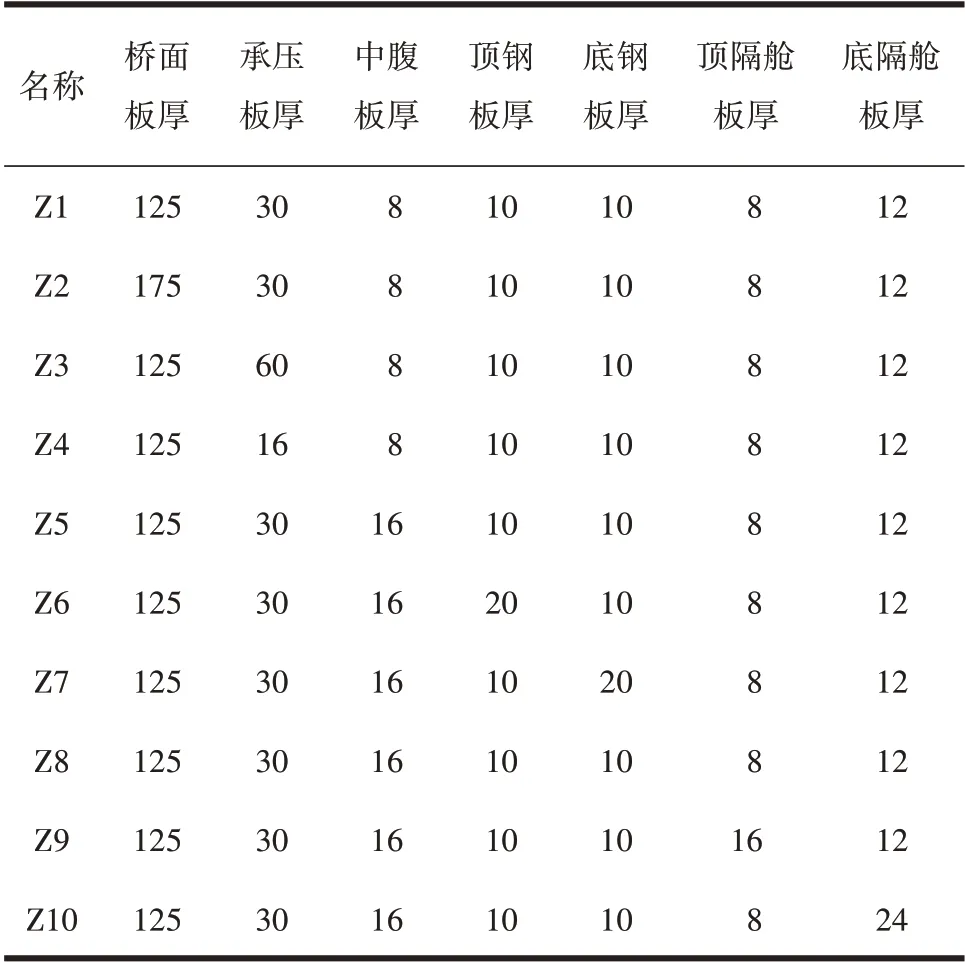
表1 参数分析表Table 1 Parameters of the finite element model mm

各参数模型计算结果如图10所示。当增大桥面板厚度时，Z2模型在C0截面处的桥面板轴力占比从45.0%提升至50.4%，承压板传递给结合段混凝土轴力占比有所减少，由32.2%变为28.1%，而剪力件的轴力占比有轻微减少，由22.8%降为21.5%。这是因为桥面板厚度增加时，加大了桥面板轴向刚度在组合梁截面轴向刚度中的比例，从而使桥面板传递的轴力比例增大。同时，由组合梁的钢结构部分传递的轴力比例减小，由承压板直接通过面压传递给结合段混凝土的轴力为组合梁的钢结构传递的轴力中的一部分，因此，由承压板直接传递给结合段混凝土的轴力占比随之减少。

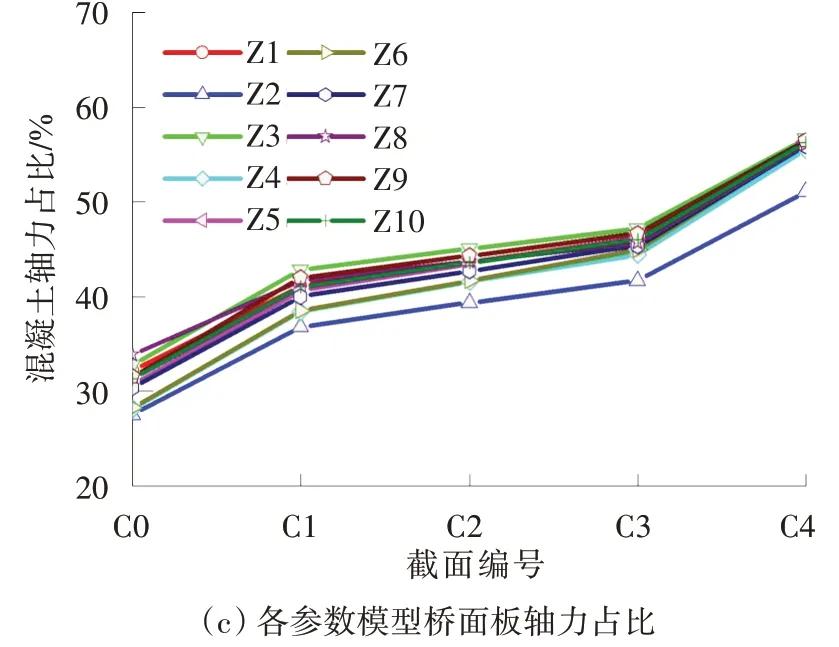
图10 各模型计算结果对比Fig.10 Comparison of calculation results of each model

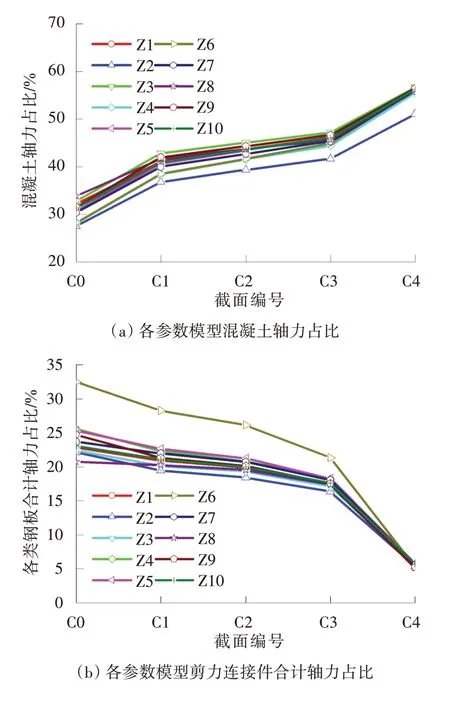
增大组合梁钢顶板厚度时，Z6模型中C0截面处剪力连接件的轴向力占比有明显提升，从22.8%提升至32.5%，同时桥面板所传递的轴力明显减少，由45%降低至39.3%，承压板传递给结合段混凝土的轴力也从32.2%降低至28.2%。这是因为组合梁钢顶板厚度增大时，减小了桥面板轴向刚度在组合梁全截面轴向刚度中的比例，因此，桥面板承担的轴向力比例减小。组合梁钢顶板厚度增大时，减小了组合梁截面中除钢顶板外的钢结构轴向刚度在组合梁全截面轴向刚度中的占比，也会减小由承压板传递给结合段混凝土的轴向力。组合梁钢顶板厚度增大时，增加了钢顶板轴向刚度在组合梁截面纵轴向刚度中的占比，增加了钢顶板传递的轴向力，而这部分轴向力会通过钢顶板上的剪力键传递给结合段混凝土，增大了剪力连接件传递轴力的占比。

由Z2～Z4号模型的计算结果可知，将承压板从30 mm增大到60 mm，不会明显改变各部分所传递轴力大小，但承压板厚度从30 mm减小到16 mm时，将使C0截面承压板传递的轴力占比从32.2%降低至28.0%，剪力连接件传递的轴力占比由22.8%提升至25.5%，桥面板由45.0%提升至46.5%。这是因为在承压板较薄情况下，增大承压板厚度，能够提高承压板的面外刚度，从而提高由承压板与结合段混凝土间的接触刚度，进而提高由承压板传递给结合段混凝土的轴力占比。当承压板达到一定厚度（30 mm）后，再加大承压板厚度不会显著提高承压板与结合段混凝土间的接触刚度，因此不会显著影响各部分传递轴力的占比。

组合-混合梁结合段影响轴力传递机理的关键参数是桥面板厚度、组合梁顶板厚度及承压板的厚度，改变其中任一参数都将使结合段内轴力分布发生一定程度的变化。当提升桥面板厚度时，桥面板自身轴力增大，组合梁截面中钢梁轴力减小，导致承压板与剪力件轴力占比减小。当提升钢顶板厚度时，组合梁截面内钢梁轴力占比增大，桥面板轴力占比减小，剪力件轴力占比增大，相应的承压板轴力占比减小。当承压板厚度较薄时，增大承压板厚度能够提高承压板直接传递给结合段混凝土的轴力占比，但承压板厚度达到一定厚度时，再增大承压板厚度则不会显著改变各部分传递轴力的占比。

传统的钢箱梁-混凝土梁结合段中，轴力传递路径的控制因素是钢箱梁板件的厚度与承压板的厚度。组合-混合梁结合段中控制轴向力分配的因素中多了桥面板的厚度，根本原因是组合梁将桥面板作为传递轴力的重要部件，大幅减少了组合梁钢板传递的轴力。因此，轴力通过结合段时，剪力连接件与承压板传递的轴力占比明显比传统钢-混结合段中的小。组合-混合梁结合段较传统钢箱梁-混凝土梁结合段的优势是可以通过调整桥面板的厚度使结合段内的轴力分布达到预期的设计状态，同时桥面板的存在减小了对承压板与剪力连接件的设计需求。

5 结论

1）组合梁-混凝土梁结合段的轴向传力部件为桥面板、埋入区的各类钢板上的剪力连接件及结合段混凝土。在承压板界面处，结合段混凝土承担的轴力为承压板所传递的轴力。轴力在结合段传递的过程中，埋入区各类钢板的轴力通过剪力连接件传递至结合段混凝土，结合段混凝土中的轴力不断增大，桥面板中的轴力通过组合梁钢顶板上的剪力连接件及桥面板与混凝土箱梁的接触面传递给结合段混凝土。

2）组合-混合梁结合段中，影响其轴向力传递路径的参数是桥面板厚度、组合梁顶钢板厚度及承压板厚度。增大桥面板厚度，能显著减小承压板所传递的轴力，提高桥面板传递轴力的占比。增大组合梁钢顶板的厚度，能减小桥面板所传递轴向荷载，提高剪力连接件传递的轴力占比。在某一范围内增大承压板厚度能增大承压板传递的轴向力占比，但承压板厚度达到某一值后，再增大承压板厚度对轴向力的传递路径影响不大。