泡沫轻质土换填路堤下地基沉降计算方法
薛国毛,李金龙,谢规球,李繁
(1.中交建筑集团有限公司,北京 100022;2.中南大学土木工程学院,湖南 长沙 410075)
为满足高速公路对于不均匀沉降控制的特殊要求,路基填筑工程中常会采用泡沫轻质土代替普通土石填料[1-5],通过减轻路堤荷载的方式,实现控制路基整体沉降量的目的。目前,主要有填土路堤、填土-轻质土路堤及轻质土路堤三种不同类型的路堤形式。在复杂的路堤荷载作用下,如何准确量化分析上覆荷载引起的地基附加应力及沉降变形是当前重要的研究课题[6-10]。
国内外学者为研究轻质土路堤下的基底沉降变形分布规律进行大量的研究。马云燕[11]依托杭州东站某轻质土填筑工程项目,通过现场监测路基的土体压力与沉降变形数据,绘制出了土体压力和路面沉降的变化曲线。路通等人[12]基于广佛快速通道某一试验段的轻质土换填路基工程,采用现场实测的方法,探究了上覆泡沫轻质土路基荷载下软土地基的应力、应变及分层沉降规律。杨春风等人[13]以某高速扩建工程为依托,结合理论分析方法和有限元数值模拟研究了轻质土拓宽路基的基底附加应力与沉降分布变化规律。李群[14]结合理论分析、室内外试验和数值仿真等方法,对泡沫轻质土置换软土路基实例的相应沉降变形特性详细地进行了研究,为轻质土换填的工程应用提供了一定的理论依据。目前,有关轻质土路基的沉降变形特性的理论研究仍滞后于实践。本研究基于弹性理论中的Boussinesq解,采用积分处理的方法,推导泡沫轻质土换填路堤下地基的竖向附加应力解析解表达式,并结合分层总和方法,建立轻质土地基沉降值的理论计算模型。探究不同路堤形式的地基沉降差异,为泡沫轻质土沉降控制提供定量分析方法。
1 轻质土路堤荷载下地基竖向附加应力
1.1 无限长均布线荷载
与公路路基的横向尺寸相比,公路路基的纵向长度可视作无限长。因此,可从平面应变的角度,假定在纵向路堤荷载为无限长均布形式,而路堤下的地基土可假定为半无限弹性形体。由Boussinesq解可知,在集中荷载作用下,半无限弹性空间体内任意点N(x,y,z)的竖向附加应力计算式为:

式中:Q为空间体上作用的集中力;x、y、z为N点空间坐标;R为N点与原点之间的距离。
在半无限空间体表面作用一无限长均布线荷载p时,对式(1)进行数值积分可得坐标面xoz内点M(x,0,z)的σz解析式,计算示意如图1所示,其应力计算式为:

图1 线荷载下附加应力计算简图Fig.1 Calculation schematic diagram of additional stress caused by the line load

式中:p为无限长均布线荷载。
1.2 梯形路堤荷载
路堤横断面内的线性分布荷载为梯形分布形式的荷载,相应的附加应力计算示意图如图2所示。
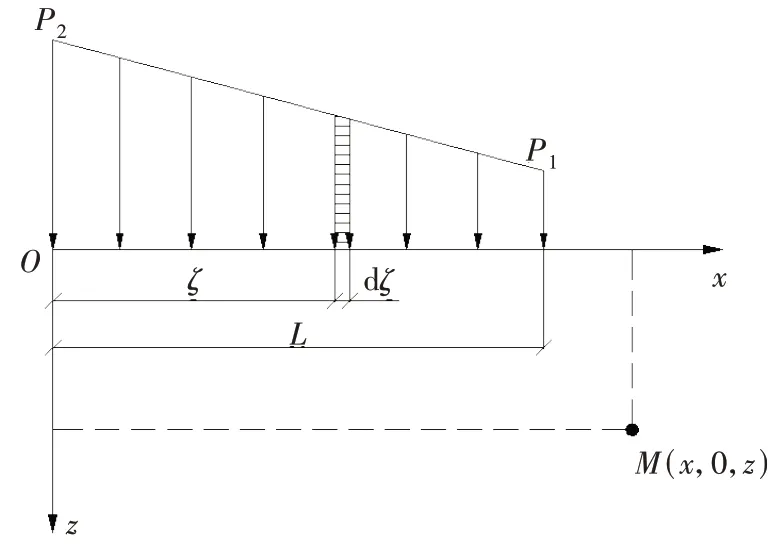
图2 梯形路堤荷载下附加应力计算简图Fig.2 Calculation schematic diagram of additional stress caused by the trapezoid embankment load
从图2可看出,荷载分布横向呈线性变化,其分布函数为:

式中:p1、p2分别为梯形分布的最小与最大荷载;ξ为荷载内任意点距原点的水平距离;L为上覆荷载的分布宽度。
对分布荷载中任意段微分dξ进行分析,相应的荷载微分dQ为:
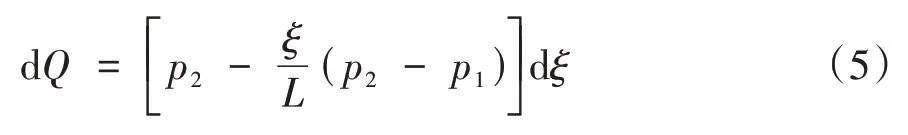
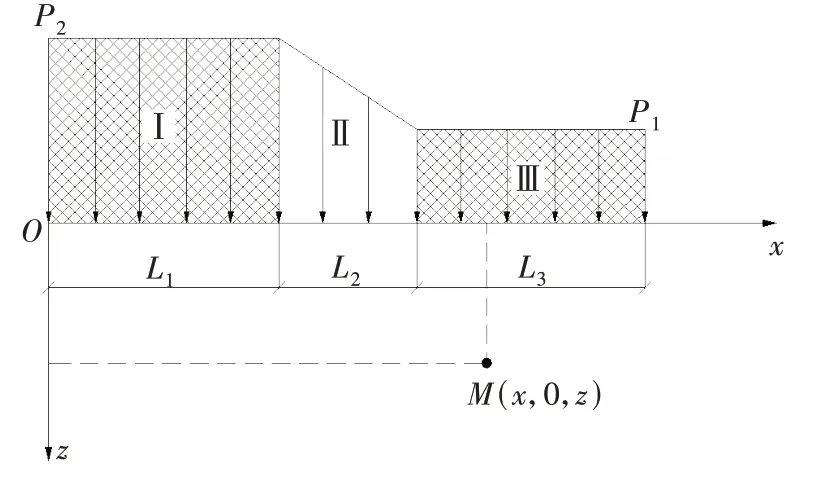
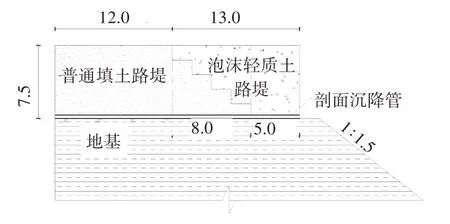
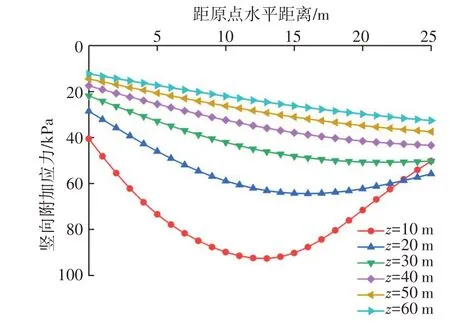
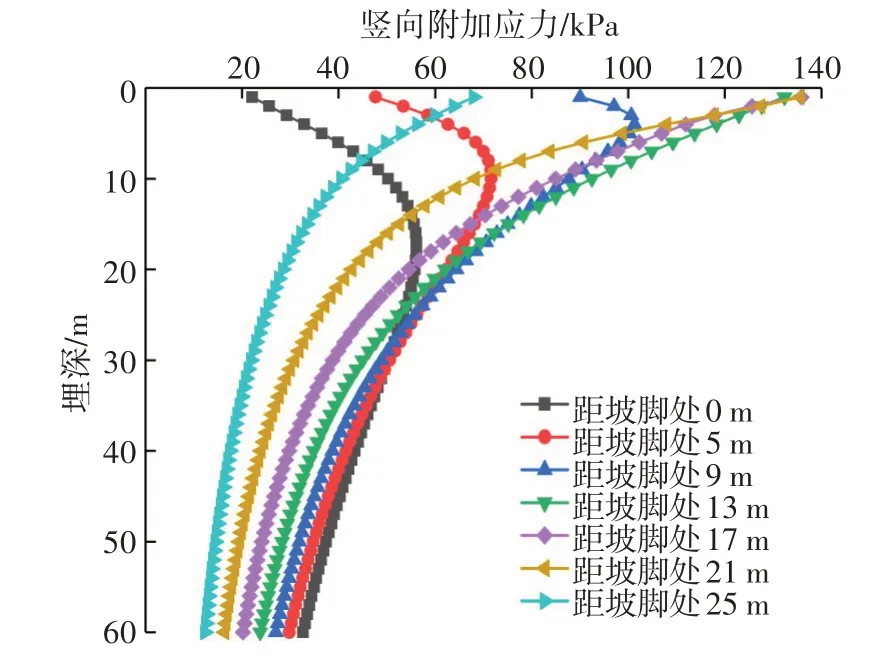
xoz平面内任意点M(x,0,z)与微段dξ的距离为x-ξ,其中,0<ξ 由梯形荷载分布特点可知,当p1=p2=p时,梯形荷载就转化为均布条形分布荷载形式,如图3所示。此时,点M(x,0,z)处的竖向附加应力变为: 图3 均布条形路堤荷载下附加应力计算简图Fig.3 Calculation schematic diagram of additional stress caused by the uniformly distributed strip embankment load 轻质土换填路堤的材料主要由普通土石填料和泡沫轻质土填料组成,两者在容重上差别较大,轻质土路堤的荷载远小于填土路堤的载荷,且填土路堤和轻质土路堤之间通常会设置台阶式衔接段,如图4所示,荷载分布形式如图5所示。 图4 泡沫轻质土换填典型路堤剖面示意Fig.4 Schematic diagram of a typical embankment section of foam light soil replacement 图5 轻质土换填路堤荷载示意Fig.5 Schematic diagram of loading of embankment filled with light soil 由图5可看出,轻质土换填路堤荷载可视为均布荷载与梯形荷载的组合。因此,在地基土竖向附加应力叠加计算之前,先需对各组成部分进行坐标系的归一化处理。 图5与图3的坐标系相同,故荷载Ⅰ引发的竖向附加应力计算式为: 在图5中,荷载Ⅱ的坐标系相较于图2的坐标系向左平移了L1,因此,由荷载Ⅱ引发的竖向附加应力表达式为: 在图5中,荷载Ⅲ的坐标系相较于图3的坐标系向左平移了L1+L2,其竖向附加应力计算式为: 对荷载Ⅰ、Ⅱ、Ⅲ的竖向附加应力解进行叠加,可得泡沫轻质土换填路基作用下的竖向附加应力计算式为: 根据式(11)并采用分层总和法计算泡沫轻质土路堤堆载下的地基沉降。假定地基土为半无限弹性空间体和有侧限压缩变形。将压缩层内的地基土划分为i层,根据地基内的竖向附加应力理论计算公式,累加各层的沉降值,得到压缩层的总沉降值。因此,路堤的基底沉降变形的计算式为: 式中:S为地基总沉降;Si为第i层土的沉降值;h为压缩层厚度;i为压缩层划分层数;hi第i层土的厚度;ε为单位厚度土体应变;ES为地基土的压缩模量。 以广连高速公路TJ05标段某区间的泡沫轻质土填筑工程为例进行计算分析。依据沉降理论计算模型得到路堤各位置处的地基沉降值与现场测量的路堤基底沉降数据进行对比,验证该计算模型的合理性。 该泡沫轻质土换填路堤可分为普通填土段、泡沫轻质土段及填土-泡沫轻质土过渡段三部分。其中,轻质土路堤段底部宽5.0 m,顶部宽13.0 m,高7.5 m;过渡段衔接形式设置为台阶式,底部宽8.0 m;填土段路堤底部宽20.0 m,顶部宽12.0 m,高7.5 m。断面尺寸如图6所示。试验区间岩土层的物理力学参数见表1。 图6 泡沫轻质土换填路堤断面尺寸(单位:m)Fig.6 Cross-sectional dimension drawing of embankment filled with foam light soil(unit:m) 现场监测利用剖面沉降仪及预埋设的剖面沉降管采集泡沫轻质土路基基底剖面沉降数据。该沉降管为特制PVC管,现场试验如图7所示。 图7 剖面沉降仪的监测示意Fig.7 Schematic diagram of the profile of the sedimentation instrument 根据表1中采集的实际参数计算地基土沉降变形理论模型所需参数取值结果见表2,沉降值计算过程分为5步: 表1 岩土层的物理力学参数Table 1 Mechanical parameters of the rock and soil layers 表2 主要计算参数取值Table 2 Value reference for the main calculation parameters 1)根据压缩层厚度确定原则,确定路堤各位置处的沉降计算深度; 2)为了方便计算,将地基压缩层的分层厚度设置为1 m; 3)针对泡沫轻质土路堤不同基底位置给出地基竖向附加应力值,计算地基压缩层分层的平均附加应力; 4)计算地基压缩层分层沉降量; 5)累积计算路堤各基底位置处的地基沉降量。 不同深度地基竖向附加应力的分布曲线如图8所示。从图8可看出,地基埋深z分别为10、20和30 m的竖向附加应力分布曲线均大致呈勺状,即泡沫轻质土路堤两侧的地基的竖向附加应力较中心位置的低,最大应力值出现在路堤中间的某一位置。地基埋深z分别为40、50和60 m时,最大应力均出现在坡脚处;且距原点水平距离越远,距离坡脚越近,竖向附加应力越大。 图8 地基竖向应力水平分布规律Fig.8 Horizontaldistributionoftheverticalstressoffoundation 地基竖向附加应力分布曲线如图9所示。从图9可看出,坡脚附近的地基竖向附加应力沿埋深方向也呈勺形分布,最大值并不在顶面处。竖向附加应力沿埋深方向先逐渐增大,在某深度位置处取得最大值后,随着深度增加逐渐减小。远离坡脚处的地基竖向附加应力随埋深的增加而递减,最大应力值在地基顶面处取得。推测造成最大附加应力位置不同的原因在于轻质土荷载的大小的差异。 图9 地基竖向应力竖向分布规律Fig.9 Vertical distribution of the vertical stress of foundation 距坡脚不同距离处的地基沉降理论计算值与现场实测值见表3和图10所示。 表3 地基沉降计算结果Table 3 Calculation results of foundation settlement mm 由图10可看出,泡沫轻质土在路堤荷载作用下,地基沉降理论值在水平位置上大致呈V形曲线分布,在距坡脚13.0 m处,即路堤中心位置的沉降量最大,越靠近路堤两侧,地基沉降量越小。 图10 地基沉降变形理论值与实测值对比Fig.10 Comparison of the theoretical and the measured values of foundation settlement deformation 由表3可知,依据本理论计算的地基最大沉降值为68.6 mm,最大实测值为62.9 mm,相差8.3%且路堤各基底位置处的沉降计算值与实测误差均≤9%,理论计算结果与实际变形吻合较好。表明基于该地基竖向附加应力理论计算模型是可靠的。 为更直观地体现泡沫轻质土在控制地基沉降方面的成效,不改变该工程路堤的相关尺寸及地基土等参数,分别设置路堤形式为全填土路堤、填土-轻质土路堤与全轻质土路堤3种形式,利用本研究的沉降理论模型,计算得到这三种路堤形式的地基沉降值,如图11所示。 图11 路堤形式对地基沉降的影响对比情况Fig.11 Comparison of the influence of embankment forms on foundation settlement 从图11可看出,3种路堤形式地基沉降值由大到小依次为:填土路堤、填土-轻质土路堤和轻质土路堤。将全填土路堤部分换填为轻质土可明显降低地基沉降,而当其全部换填成轻质土后,整体地基沉降变形降低了68%。这是因为轻质土的容重远小于填土的容重。本实例中所采用轻质土的容重仅为填土容重的1/3,换填成轻质土后地基的上覆荷载减小了2/3,沉降量也随之大幅降低。 1)在弹性理论解的基础上,采用数值积分的方法求解了梯形、均布条形的竖向附加应力解析解,并通过叠加计算获得了轻质土路堤下的竖向附加应力场; 2)依据推导出的地基土竖向附加应力分布的解析解,结合分层总和的沉降分析方法,构建了泡沫轻质土换填路堤荷载下的地基沉降理论计算模型; 3)通过工程实例分析,结合现场实测数据,验证了该沉降计算模型的可靠性。根据沉降分布曲线,在路堤荷载作用下,泡沫轻质土地基的沉降理论值在水平位置上大致呈V形曲线分布,路堤中心位置处沉降量最大,越靠近路堤两侧,地基土的沉降量越小; 4)通过换填路堤分析路堤形式对地基沉降的影响,研究结果表明:采用换填轻质土能有效降低地基土的上覆荷载,降低整体沉降。因此,通过调节泡沫轻质土的容重可实现调节地基沉降量的目的。
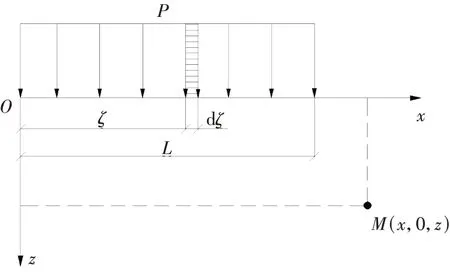
1.3 均布条形路堤荷载

1.4 轻质土路堤荷载




2 轻质土路堤荷载下地基沉降
3 实例验证与分析






4 结论

