因倍数概念教学中数形结合的妙用

江苏泰兴市鼓楼小学教育集团鼓楼校区（225499） 赵丽君

何为数形结合？数学家华罗庚有过经典总结：“数缺形时少直观，形少数时难入微。”这句话深刻揭示了数形结合的内涵。实际教学中，广大教师正是明白这一点，才不遗余力地用“形”的直观去弥补“数”的抽象，用“数”的严谨去弥补“形”的粗放，让数和形完美结合，交相辉映，将数形结合的教学功能发挥到极致。由此，数形结合既是一种研究数学问题的思想方法，同时又可以看成是揭示数学知识逻辑的有效手段。下面笔者将以数形结合为切入点和研究思路，对“倍数与因数”的教学进行改进。

一、借“形”引出概念

【教学片段1】

师（出示图1、图2）：某个运动会开幕式上，中日两个国家的体育代表团分别站成两种队形，计算一下，中日两国各派出多少人参加这次运动会的开幕式？

图1

图2

生1：根据图1列队的情况，可以算出中国代表团的人数为9×4=36（人）。根据图2列队的情况，可以算出日本代表团的人数为5×7=35（人）。

师：在9×4=36这个乘法算式中，按照以往的称谓，相乘的两个数9和4称之为乘数，而相乘所得的结果36则称之为积。在队列中，9是每行站队的人数，4则表示一共站了4行，36则是这个队列中运动员的总数。

师：联系今天学习的课题“倍数与因数”，请大家猜测，在计算图1中国代表团的人数的乘法算式中，哪一部分是因数，哪一部分是倍数。

生2：在9×4=36这个算式中，4和9是36的因数，36是4和9的倍数。

师：现在请大家再次观察图2的队形，重点关注行数、列数和总数，并对照匹配的乘法算式5×7=35，说说哪一部分是因数，哪一部分是倍数。

生3：列数5与行数7都是总人数35的因数，总人数35是行数5和列数7的倍数。

（根据学生回答板书，如图3）

图3

【评析】倍数与因数是定义两个自然数的倍率关系的，这种关系可以用乘法算式直观反映出来。在自然数的乘法算式中，乘数和积就是因倍数关系的直观体现。可见，这部分新知完全可以脱离乘法算式，只要乘法算式中的各数字为非0自然数即可。仅仅依靠这种形式上的关联还不够，运动会开幕式体育代表团队形的情境，不但可以激发学生的学习动机，而且能借助图形的直观性从另一个维度呈现因倍数的关系：行数和列数是因数，队列总人数为倍数，而且它们是相互依存的。这样一来，可以观察出总人数就是行数和列数的整倍数，因为行数和列数以及总人数必须全部是整数。之后再来对照计算总人数的乘法算式，三管齐下，因倍数的概念就会非常清晰通透。这种融入数形结合的教学方法，可谓匠心独具，将陌生的新知在不知不觉中渗透到旧知中，毫无痕迹。

二、用“形”抽象概念

【教学片段2】

师：倍数与因数是两个举足轻重的概念，是分数运算中通分和约分的奠基内容，所以请同学们务必学好。

师：仿照前面习得的方法，请大家随机写出2～3个不重复的乘法算式，并在点阵图（如图4）中圈画，然后与同桌互相说说“谁是谁的因数，谁是谁的倍数”。

图4

师（出示图5）：这是“神算子”写出的算式和配图，正确吗？如果没有异议，请说说“谁是谁的因数，谁是谁的倍数”。

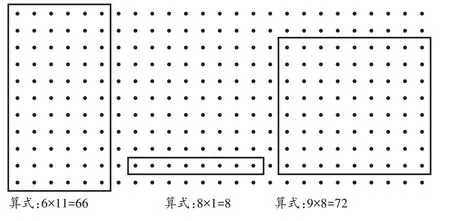
图5

师：像这样具备因倍数关系的数对多吗？

生（齐）：多。

师：谁能一口气说完？

生1：唯一的办法就是用代数式表示，这样可以代表所有存在因倍数关系的数对。

师：好极了！如果分别用字母a、b、c表示3个不同的数，如何表示它们之间的因倍数关系？

生2：a×b=c（a、b、c均为大于0的自然数），则c为a、b的倍数，a、b为c的因数。

【评析】自主探究环节中的“圈画、列式、陈述”，其目的在于构建因倍数的几何模型，即在点格图中根据行数和列数来反映因数，用总数来反映倍数。借助这个几何模型，它们之间的数量关系也呼之欲出——行数乘以列数等于总数，这就意味着因数乘以因数等于倍数。“神算子”的作品中，有只有一行的，也有列数大于行数的。这既提供了常规例子，又展示了特例——行数为1。在此基础上，学生抽象出字母表达式，就顺理成章了。显然，教学片段1的情境以及教学片段2的“圈画、列式与陈述”，只是从情境、图形、语言和操作几个方面让学生理解概念，最后抽象出的字母表达式才是终极形式，字母表达式才是概念内涵的核心。那么，大费周章地运用这么多表征来让学生理解概念有无必要？曾有美国权威学者采用图6揭示概念的发展过程：“实物操作只是展示数学概念的初级形态，图像、语言、表达式才能起到抽象作用，并且深刻揭示概念内涵。”这一观点就是概念教学的灯塔：在教学中，任何一种表征都不应被忽略，各种表征应该串联起来形成合力，帮助学生学会根据客观需要选用合适的表征来理解。

图6

三、“形”助理解规定

【教学片段3】

师：以前学习的倍数，其实还可以用除法算式c÷a=b（abc≠0）表示，这里a、b、c的取值范围不作限定，整数、小数、分数均可，只要不为0。今天学习的倍数则用乘法算式来理解，形如a×b=c的算式就可以表示因倍数关系，此处a、b、c的取值范围是否还是那么随意？

生1：我认为不作限定，整数、小数、分数均可，只要不为0。

生2：不对！这次学习的倍数与以前学习的倍数大有不同，此处的a、b、c必须为非0自然数。

师：请说说你的理由。

生3：我们是在点阵图中提炼因倍数概念的，行数、列数、总数都必须是非0自然数，这是常识。

师：“倍数”与“倍”只有一字之差，它们到底有何异同？

生4：从数量比较上看，它们反映的都是两个数的倍率关系。不同点是，“倍”是一个广义宽泛的概念，其中的“数”可以是所有数型，只要排除0；“倍数”是一个狭义的概念，其中的“数”严格限定为非0自然数，规定极为严苛。

【分析】“倍数”是什么？要向学生说清这一概念，不能仅靠范例，因为范例只是一面之词，容易让学生“一叶障目不见泰山”。如果此时与相近易混的概念“倍”做一番比较，那么学生的眼界和思路将会更加宽阔，看问题的角度也会更全，分析问题时会更全面。通过比较辨析，学生弄清二者之间的异同点。相同点是都表示两数的倍率关系，都可以用乘除法算式表示。不同点仅仅在于称呼和取值范围的不同——“倍”只要不为0，所有数型都可，因为这是由除法的性质决定的，除法算式的结果可以是整数、分数、小数等各种形式，“倍”就是除法算式中衍生的一个概念，除法算式才是“倍”这个概念的母体；而“倍数”的概念则是由特殊的乘法算式决定的，特殊之处就在于是计算圈画出的点子图的总数时，行数、列数必须都是整数，所以这里的数只能是非0自然数。通过对比辨析，学生调用在点子图中积累的直观经验论述了因倍数概念的内涵本质。在此，借助直观的点子图还有另一好处，那就是让“0除外的自然数”这一规定显得合乎情理。

四、依“形”建构模型

【教学片段4】

师：点子图帮了我们的大忙，有了它，因倍数概念就非常浅显易懂，以后找倍数就可以回想点阵图。请大家思考一下，借助点阵图寻找某数的倍数，其实是对应地先确定什么，再找什么？

生1：先确定一行的点数，再逐步递增行数计算总数。

师：下面请大家依据他的描述，自己动手圈画一下，试着找一下7的倍数。

（学生边汇报教师边播放课件，最后得出图7）

图7

师：通过刚才的操作，请归纳找一个非0自然数a的倍数的方法。

生2：a×1，a×2，a×3……

生3：依次找a的1倍、2倍、3倍……

师：根据自然数的定义，倍数的数量是无限多的，有最小的倍数，一个数的最小倍数就是它本身，没有最大的倍数。

【评析】“圈画点阵图，并尝试找出7的倍数”的活动，一方面，让学生体验找倍数的直观方法，进一步领悟倍数的概念；另一方面，在这种直观操作中，找倍数的方法也不言自明：一个数就是每一行的点数，倍数就是在不同行数下的总点数。通过圈画，学生会发现，求一个数的倍数，就是将这个数量不断复制，复制一次就有一个倍数出现，倍数可以无限大，这映射到乘法算式里就是将目标数从小到大不断连续乘以自然数——从这个数的1倍开始找起，接着找它的2倍、3倍……同时，倍数的特征也一览无余：一个数的最小倍数就是它自己，倍数可以无穷大，相邻两个倍数的相差值是它的本身。

因倍数本是一个代数概念，这个概念的内涵本身并不复杂，可以直接借助乘除法算式来定义，只不过，一旦与乘除法发生勾连，那么概念的范围势必会受到学生前认知的干扰，而倍数是专门针对非0自然数设计的，也就是只有正整数乘法算式中，才可言倍数概念。这样一来，学生的理解难度就会骤然加大。在教学中利用数形结合之后，倍数概念必须定义在非0自然数范围内就显得天经地义，因为任何队列的列数和行数以及总数都必须是正整数，这是与客观现实相适配的。因此，用数形结合的方法来理解倍数概念可以精准揭示概念内涵。