不确定性工时下甲板作业的前摄性鲁棒调度

万兵，苏析超，郭放，韩维，梁勇

海军航空大学，烟台 264001

航母是海上“移动基地”，其作战效能的发挥直接由搭载舰载机的出动能力来决定[1]。舰载机在出动前都要进行以充添加挂为标志的使用保障工作，即加油、注水、挂弹、出动前检查等时序要求工序，但由于受到甲板空间、机位、保障资源数量等的限制，在对舰载机机群进行保障时，会出现竞争使用资源的情况，影响到各单机保障工作，以至于增加了单机的保障准备时间，进而影响到机群作业进度，因此甲板作业的科学调度、统筹规划需求迫切。此外，工时不确定性导致实际作业与调度计划出现偏差，降低方案的可执行率，影响舰载机出动效能。综上，开展不确定工时条件下甲板作业鲁棒调度优化研究，对应对不确定性工时扰动、竞争性保障资源冲突，确保各阶段作业协调有序，并对提升舰载机出动能力与航母作战保障水平意义重大。

近年来，围绕甲板作业调度学者主要从出动回收全流程和分阶段优化研究，美国麻省理工大学人工智能研究所Ryan等[2-3]开发了舰母甲板作业规划决策支持系统，建立舰载机全流程作业混合整数规划模型，引入“人在回路”的决策方法，并用优化器Gurobi/Cplex进行求解，比较了自动算法与人工经验的决策效果。Michini和How[4]提出了基于专家经验的逆向强化学习机制，完善了智能调度策略，但对不确定环境下的决策问题效果不佳。Zheng等[5]针对全流程连续作业提出了基于学徒学习的智能调度算法，算法较好地跟踪了专家经验，但作业过程模拟较简单且所选定特征量难以反映真实场景，其智能决策结果仅提供顶层的任务规划，相比于基于AnyLogic[6]全局信息、动态交互的全流程模拟决策，其任务规划效果无法评估。文献[7-10]则从调运、甲板作业、出动及回收等方面进行基于启发式算法求解。Qi和Wang[11]提出层次任务网络规划架构采用回溯算法，解决了舰面保障任务耦合问题，其分层规划思想贴近指挥员-飞行计划-调度员-调度方案-执行的垂直体系，是调度分解的一种思路，但回溯法仅为现行约束规划的一种策略，仍有较大改进空间。综合现有研究及甲板作业特点，分阶段研究集中对起降作业中调运、保障等具体作业调度的优化生成，而全流程研究对细节忽略较多，仅适合做作业任务规划，可作为时间窗约束嵌入各阶段作业调度计划。研究分阶段中时长占比最大的甲板作业保障，相比文献[9]给出的柔性车间调度模型，对于人力与设备分配及时序编排问题，资源受限项目调度模型(Resource Constrained Project Scheduling Problem, RCPSP)更接近其本质。故对多机甲板作业保障，实则完成具有工时不确定和空间约束的多项目资源受限项目调度优化工作。

针对该阶段调度研究，Cui等[12]综合考虑了多机保障流程约束和保障单元约束，建立了多机一体化机务保障调度模型；笔者团队[13]引入“油电气液”等勤务保障的协同作用和约束限制，建立了机务勤务一站式保障调度模型。刘钦辉等[14]考虑了甲板站位空间因素对舰载机作业的影响，设计了融合串行调度和并行调度的混合调度算法生成多站式保障调度方案。对上述多站式、集中式和一站式保障，甲板作业集中式保障能力强、利于大规模机群分波出动，但资源调度复杂度高，故重点研究该模式下的调度优化。

与现有的经典多项目RCPSP问题相比，有以下几点不同：① 资源覆盖所带来的空间约束问题，比如甲板上有多个加油站，但对某一加油站则仅能覆盖保障其附近2个停机位，故即便在加油站资源充裕时上述2机位由于空间约束无法同时加油作业；② 资源使用的容量约束，对同一类资源除数量限制外，同时使用的容量也有要求，比如充氧氮站/车同时工作的站数不得超过某阈值；③ 机队保障作业并非单机项目调度的并行叠加扩充，在其合成的多项目调度中，不同项目的相同工序(如加油等)存在工序耦合，除前两个因素外，指挥员或调度人员的偏好会导致并行项目流图间存在耦合时序关系；④ 不确定工时显著服从一定的概率分布，容易采用Monte Carlo模拟其随机规律。

目前，舰载机不确定性作业调度领域文献较少，Yuan等[15]提出预-反应式调度策略，突出采用重调度策略来适应不确定性；Su等[16]基于双种群差分进化算法采用工时三点估计法进行鲁棒动态调度研究，通过设定最大适应不确定性的鲁棒指标搜索最优基线调度；李亚飞等[17]提出基于多智能体强化学习DQN(Deep Q Netwrok)的舰载机保障作业实时调度方法，立足部分可观测的弥补决策过程(Markov Decision Process，MDP)过程开展全流程动态环境下的在线学习与离线调配。针对不确定性的Multi-RCPSP问题，可采用随机调度、模糊调度、多智能体调度、重调度或基于启发式规则的在线调度方法。而调度更突出计划性与可执行性，目前研究较多的是鲁棒调度技术[18-19]，鲁棒性指标有完成时间裕度、最坏情况最小及按时完成率最大等，主要方法有基于关键链的时间缓冲法[20]、两阶段Benders-Cuts分解[21]或多阶段列生成算法[22]，前者是基于调度生成机制的智能优化算法，处理大规模问题占优；后者采用主-子问题对偶分解的优化器精确求解，应对中小规模问题效率极高。但当前不确定调度领域缺乏前摄计划性调度，而这可超前指导甲板作业执行。

综上分析，以舰载机甲板集中式保障模式为背景，重点开展具有随机分布的不确定工时的鲁棒调度研究，提出机队按时完成概率，最大完工期望和方差等指标构建综合鲁棒性指标，依托前摄性调度基于改进Memetic[13]元启发式算法(Improve Memetic, I-Memetic)生成满足鲁棒性能的基准调度方案，提升机队在甲板作业周期内应对工时不确定的抗扰动能力，确保机队出动按节拍连续可靠。

1 问题描述

舰载机甲板集中式保障(Aircraft Carrier Deck Centralized Operation, ACDCO)是指舰载机机群出库转运或着舰回收后，根据甲板布列计划，调运至指定保障停机位，并在这一阵位完成直接出动准备或再次出动准备所涉及的机务勤务保障作业，甲板保障全程只需牵引调运1次。而前摄式鲁棒调度[20](Proactive Robust Scheduling, PRS)是指在实际保障开展前，根据历史作业数据信息对随机因素进行预测，预先采取措施，以生成抗干扰能力较强的基准调度方案。因此，舰载机甲板集中式保障前摄鲁棒性调度(ACDCO-PRS)问题可描述为：在满足工序保障流程约束和资源约束条件下，通过预先构建基准调度计划，合理地规划作业时序和分配工序保障所需的人员设备等资源，使得在实际工时不确定扰动下，仍能保证机群保障作业完工的高效性和鲁棒性。

根据甲板保障作业约束条件属性，可将其划分为作业流程优先序约束和资源约束两大类，其中资源约束又可细分为人员、设备等可更新资源约束站位空间资源约束和供给资源约束。

1) 作业流程约束。舰载机在入位系留后，将进行装备检查、加油、充气、军械等一系列机务勤务保障作业，若将单机的保障活动抽象为1个项目，那么波次出动的机队保障作业流程可采用增广拓展AON(Activity on Node Network)图进行描述，可参考文献[23]。然而不同于传统多项目调度，由于固定资源站共用所带来的空间约束致使不同项目间相同工序出现交叉耦合，需添加额外优先序，使得模型求解更为复杂。

2) 人员、设备资源约束。保障人员按专业分为特设、军械、机械、航电等类型，而保障设备主要包括为舰载机提供油、电、气、液等勤务保障的固定资源站。图1为俄罗斯库兹涅佐夫航母的人员设备资源覆盖与转移示意图。资源配置竞争冲突明显，多机依序分配不同设备站资源。约束有以下特点：① 同一时刻工序占用资源总量限制；② 任务结束后释放资源并转移至其它工序；③ 固定设备覆盖因素带来资源转移范围受限，即固定资源仅为辐射区域飞机用；④ 人员约束可灵活设置成单机组保障和跨区域统筹，从提高效率角度可采用全域分配模式。

图1 某航母甲板资源保障示意图

甲板作业中，由于人员熟练度、资源转移、设备安装、飞机状态、甲板突发状况及备弹数、加油量等不同客观因素影响，工序工时具有随机性，假定可从历史作业信息中通过假设检验方式获得该不确定性相应概率分布函数，那么采用传统随机调度可以解决调度方案生成，其做法是针对1组随机抽样的工时进行多调度方案设计，通过多备份方案与重调度策略匹配不确定性。然而从甲板作业安全有序角度应减少项目执行中的重调度，因此提出基于鲁棒性指标的前摄性调度，可较好地平衡计划执行性与项目完成率，以满足机队出动回收作业全流程有序衔接、连续循环。

2 ACDCO-PRS模型及求解构架

模型建立前，作如下假设：① 作业过程不可中断，全程无人员和设备变更；② 同一人员或设备某时刻只能保障1个工序；③ 人员设备等转移时间远小于工序保障用时，可在不确定性工时中给予考虑，在本模型中忽略；④ 不考虑重大故障和任务变更等其它干扰；⑤ 不确定工时的分布规律已知；⑥ 人员保障范围为全域作业；⑦ 飞机进行原位机务勤务保障，无需中途调运。

2.1 模型参数及决策变量

主要参数及决策变量定义如表1和表2所示。

表1 模型参数及符号定义

表2 决策变量定义

2.2 数学模型

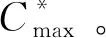
(1)

式中：F为目标优化函数值；ω为第2个目标VCmax的加权值；Pr为完工满足(·)内容的概率。

约束条件设置为

(2)

(3)

∀i,e∈I,∀j∈Ji∀g∈Je

(4)

(5)

(6)

∀i∈I,∀j∈Ji,∀k∈Ks, ∀t>0

(7)

(8)

(9)

(10)

(11)

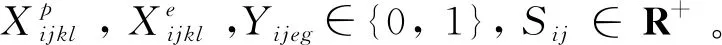
式(2)表示第i架舰载机入场系留完毕后才能开始保障，j=1代表开始的虚工序；式(3)表示各舰载机工序的紧前关系约束；式(4)表示占用相同资源的工序需按优先级依次开展，其中BM为足够大实数，确保不等式恒成立；式(5)和式(6)分别代表保障人员和设备的数量约束，即同一时刻所有处于执行状态的工序对某类专业人员或某类设备需求量需小于其数量上限；式(7)表示空间资源约束，即占用同一舰载机站位空间的不同工序不得同时作业；式(8)代表供给性资源约束，即任意时刻对某供给性资源的需求不超过其供给能力限制；式(9)为设备及人员的保障范围约束，即只对在保障设备及保障人员的保障范围之内的舰载机进行保障；式(10)和式(11)分别为工序对人员和设备需求量的分配量的匹配约束。

2.3 模型求解框架

根据ACDCO-PRS模型的决策变量定义，需要优化的内容包括保障时序方案和人员、设备分配方案。对此，设计ACDCO-PRS鲁棒性调度优化方法的求解框架如图2所示。

图2 ACDCO-PRS求解总体架构

求解过程包含3个主要环节：一是通过三阶段鲁棒调度生成机制得到鲁棒性基准调度方案，其中依次进行基于串行调度的基准时序方案、鲁棒性设备调整和鲁棒性人员分配3个阶段，通过所设计的设备调整鲁棒性和人员分配鲁棒性指标，使得改进后方案的鲁棒性相对基准时序方案的鲁棒性有局部提升；二是提出预约束调度策略，其作用是针对给定的基准调度方案，在不确定工时干扰下按照既定的调度规则生成的实际作业执行进程，从而通过Monte-Carlo仿真映射至式(1)的鲁棒性目标；三是针对鲁棒性目标，设计了I-Memetic算法对基准时序方案进行优化搜索，最终获得优化的鲁棒调度方案。

3 前摄性鲁棒调度生成机制

舰载机甲板集中式保障因涉及多架舰载机、多种资源在不确定工时下的有效协调，是1个多约束、大规模的NP-hard优化问题，与基于活动列表的经典随机调度不同，实际作业应基于基准调度进行。对此应生成前摄性鲁棒调度，包括生成初步作业时序计划及人员设备分配方案的基准调度方法，解决工时不确定条件下的基准调度执行的预约束调度策略。从而实现对给定基准调度，在不确定工时扰动下按既定调度规则生成的实际作业进程，并由2.3节完成其鲁棒指标评价。

3.1 基准调度方案生成

针对舰载机甲板集中式保障基准调度方案所包含的时序方案、保障人员分配方案和保障设备分配方案等3个核心要素，提出1种三阶段鲁棒性基准调度方案生成机制：首先在第一阶段，基于串行调度生成机制(Serial Schedule Generation Scheme, SSGS)产生基准时序方案，在给定时序方案下，由于固定资源站保障范围的约束，设备分配不具备随意变更特性，如某加油站的保障对象由舰载机A更换至舰载机B后可能导致前者无覆盖加油站而延迟等待，因此在本阶段基准时序方案还需匹配设备预先分配方案；相反地，人员分配具有互为替换性，可在后续阶段根据时序方案进行匹配。其次，考虑人员和设备的鲁棒性分配，在给定时序方案的前提下，资源分配方案可有多种选择，所形成的资源流网络也千差万别，文献[24]研究表明，资源流网络所增加的额外前后序关联数越少，活动之间的时差越大，则项目调度的鲁棒性越强。基于这一原则，阶段二和阶段三分别提出鲁棒性设备分配调整机制和人员分配机制，从而形成完整的基准调度方案。

3.1.1 基于串行调度的时序方案

取各工序期望工时Edij为输入，基于项目工序优先序，采用文献[16]所提出面向甲板保障约束的串行调度生成机制得到保障的时序方案{[Sij,Eij]}(i∈I,j∈Ji)，其中工序所需设备的选择采用基于覆盖范围内剩余工序作业时间最少优先规则(Minimum Total Processing Time Remaining in Covering Area, MTRCA)，即每个决策时刻选择空闲设备中覆盖范围内的舰载机待保障工序时间和最小的设备，从而得出设备的预先分配方案。通过MTRCA分配，一方面缓解覆盖较多舰载机工序的设备的使用冲突，使工作负载均衡；另一方面避免设备使用过度集中造成保障总时间的延迟。

基于时序方案生成机制的本质是左向对齐调度，使得工序的时序计划尽量靠时间轴的左侧安排，即尽早安排工序的开始时间。为进一步缩短总的工期，往往结合右向对齐调度一同使用，双向迭代算法即为一类代表。

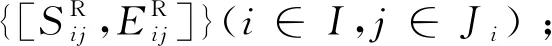
图3 左右对齐调度编排示意图

3.1.2 设备分配调整的鲁棒指标

上节生成的基准方案为仅考虑优化时序的初始配置，还需作进一步调整以应对不确定工时扰动，增强调度鲁棒性。

定义1具有资源转移关系工序对(Oij,Oeg)的空闲时差(Pairwise Flaoat,PF)

(12)

式中，Oij∈Peg表示工序对(Oij,Oeg)间无流程逻辑和资源流向的先后约束关系；否则，后续工序必然受前序工序影响，此时空间时差虽无缓冲意义，但并未引入额外资源流，因此具备更优的鲁棒性，不妨令其取值加上极大值BM。

由于当前阶段人员并未分配，设备分配未确定，资源流仅包括空间资源。考虑到活动空闲时差对鲁棒性指标的保护效果并非随着空闲时差的增加而线性递增，故引入设备分配鲁棒性指标。

定义2基于指数递减的效用函数来描述设备分配鲁棒性的替换指标RE:

(13)

以指导搜索在不破坏原有时序方案情况下的鲁棒最优设备分配方案，其中Qk为第k(k∈Ke)类设备具有相同设备转移关系的工序对集。

具体到设备的调整操作时，仅需确保每次调整后的局部鲁棒性优于调整前，则设备分配的全局鲁棒性必将持续优化。引入2类调整操作：①交换，即分属不同设备的两个工序互为交换设备分配，实施交换的前提是交换后仍满足设备覆盖范围约束，且工序保障时序不会与其他工序干涉；②插入，即将工序由原所属设备转移分配至另一设备，实施平移的前提除了满足设备覆盖范围约束外，工序保障时序不会与目标设备的所有工序存在干涉，如图4所示。

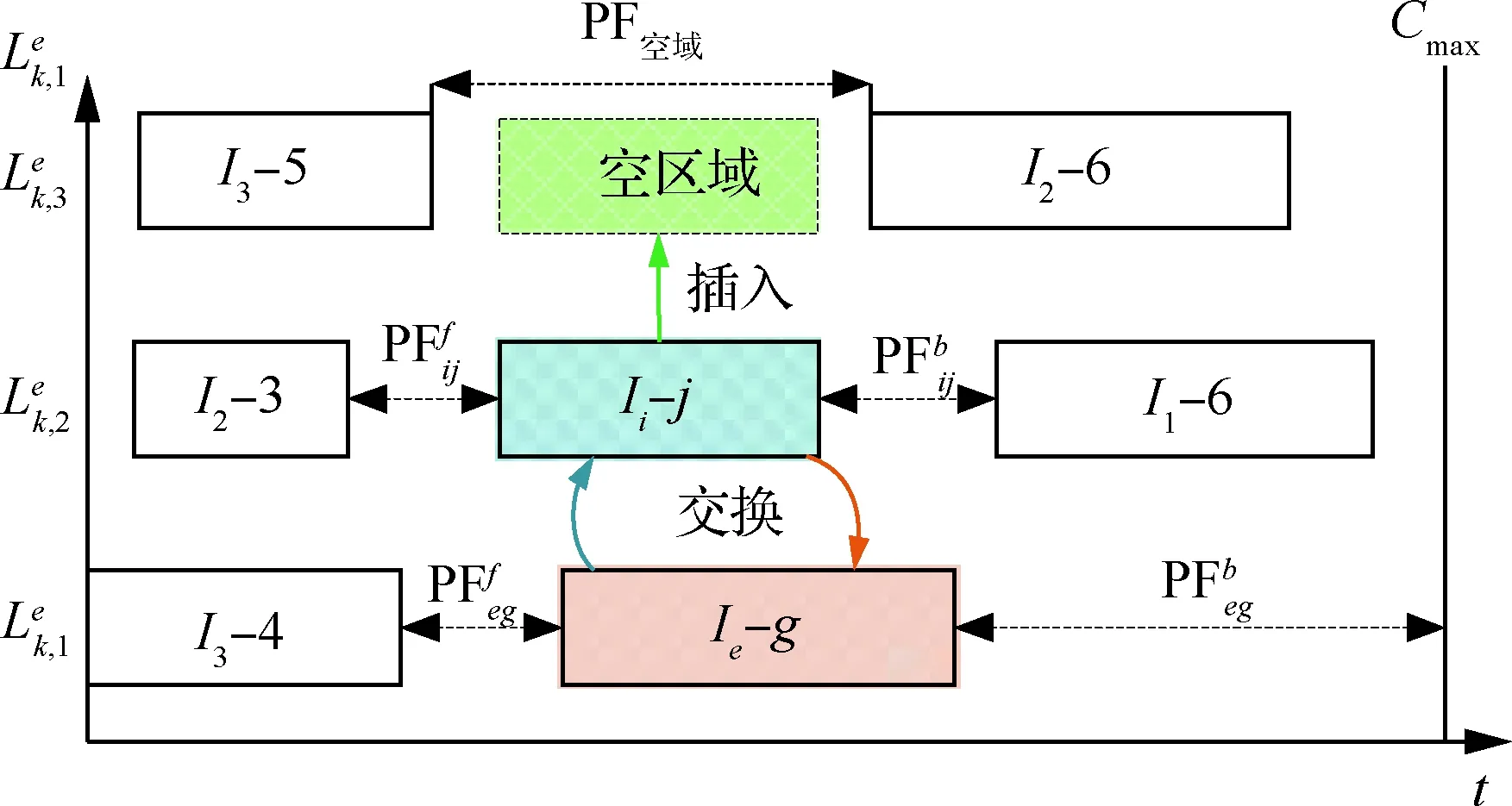
图4 鲁棒性设备调整示意图

3.1.3 人员分配的鲁棒指标

结合工序时序和设备分配方案完成人员分配，人员分配的鲁棒性指标与上节类似，借鉴空闲时差的概念，

定义3Oij与第k类可分配人员r之间的空闲时差

(14)

式中：LFTkr表示第k类保障人员r的最近保障完成时刻，对应最近完工的工序Oeg，该值相对于分配时刻Sij而言，并随着分配的深入而递增，Pij表示的Oij紧前工序集的构建在式(12)基础上新增了保障设备分配所形成的资源流前后继约束。

定义4利用指数型效用函数作为人员分配的鲁棒性指标，

RPijkr=exp(-IFijkr)

(15)

进而针对不同专业类型需求选择鲁棒性指标最小的人员进行分配。

3.2 预约束调度策略

甲板作业中，以基准调度作为不确定工时调度策略的参照，若采用基于工序优先列表的调度策略需提前将基准计划按照工序开始时间升序排列转化为工序优先列表。基准调度计划由串行调度机制生成，若直接采用基于资源调度策略CRB、接力赛或时刻表策略则会将原始计划的积极进度特性破坏并转变为非延迟进度特性，从而劣化了解的性能；而基于工序调度策略CAB受制于优先级列表，导致无约束限制，本可提前开始的活动必须延迟至活动列表优先的工序开始后。

综合调度策略优劣，提出一种面向舰载机甲板作业随机调度的预约束策略(Pre-Constraint policy,CPC)，该策略同样以并行时间递推调度为主线，确保满足约束的工序尽早调度；而在调度开始前，将人员约束、设备约束、空间约束和供给约束预先转换为工序之间的逻辑约束关系，从而保证了基准调度方案的积极进度特性不受并行调度的影响。具体预先约束转换过程如下：

1) 将基准调度方案中各人员、设备的保障资源流转换为工序之间的完成—开始型紧前约束，如某保障人员所分配的保障工序Oij优先于Oeg，则在初始流程约束中增加OijOeg前后续约束，并更新多机保障工序流程网络D=(V,AN,AR)。

2) 将基准调度方案中各工序占用相同空间的前后顺序，按照人员、设备保障工序流的转换方式，同样转变为完成—开始型紧前约束。

4 鲁棒调度的I-Memetic算法

基于上述鲁棒调度方法，在给定基准时序方案下，可相应得出鲁棒性设备和人员的分配方案，进而通过预约束随机调度策略结合Monte Carlo仿真方法求解基准方案的鲁棒性指标。然而，基准时序方案的优劣将直接影响到保障作业鲁棒性的大小，常规基于启发式规则制定的基准时序方案并不具备面向鲁棒性指标的优化性能。对此，本文设计一种结合双种群遗传优化和自适应变邻域局部优化的I-Memetic算法对基准时序方案进行优化。

4.1 算法总体流程

I-Memetic算法流程如图5所示，步骤如下：

图5 I-Memetic算法流程图

步骤2对当前种群PopL进行遗传进化，采用右向对齐生成时序方案，根据阈值评估机制进行Monte Carlo鲁棒性指标解码，每个个体的进化操作按如下步骤执行：

1) 取左种群PopL的第i个个体作为父代个体，再从除父代个体之外的PopL剩余种群中随机选择2个互不相同的个体，根据二元锦标赛策略，选择其中适应度值最优的作为母代个体。

2) 对父代个体和母代个体执行基于资源利用率的两点交叉和变异操作，生成2个子代个体。

3) 对2个子代个体分别进行基于串行调度机制的右向对齐调度，得到时序方案和预先设备分配方案。

5) 在确保预先设备分配不变的条件下，通过左向对齐将原时序方案转化为标准时序方案，进而采用鲁棒性设备分配调整机制和人员分配机制形成完整的基准调度方案。

6) 基于预约束调度策略，在Monte Carlo随机采样的作业场景下，对基准调度方案进行调度并统计式(1)中的鲁棒性指标。

7) 对比2个子代个体的适应度值，择优保留，以右向对齐形成的初始调度时序方案的开始时间修正原父代个体编码，得到所有子代新个体组成的右种群PopR。

步骤3判断当前累积评价次数是否达到最大评价次数，若是，则迭代终止，并输出最优基准调度方案和鲁棒性指标；否则，转入步骤4进行右种群的遗传进化。

步骤4对右种群PopR进行遗传进化，具体每个个体的进化操作步骤与左种群进化相同，其中的操作差别在于以下3点：① 时序方案由基于串行调度机制的左向对齐调度生成；② 由于左向对齐生成的时序方案即为标准时序方案，因此相对5) 中仅需进行鲁棒性人员分配和设备调整；③ 最终保留的精英子代的编码采用左向对齐形成时序方案的结束时间来修正，得到所有子代新个体组成的左种群PopL。

步骤5对当前历史最优解进行自适应变邻域搜索，若有改进，则修正编码并替换左种群PopL中的最劣解，并将新的左种群返回步骤2。

4.2 编码与评价

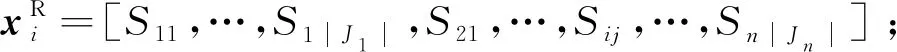
为确保基准方案下的保障作业尽早开始，标准的时序方案由左向对齐操作生成，针对右向对齐所生成时序方案的鲁棒性评价，需首先在确保设备分配不变的条件下，通过左向对齐将其转化为标准时序方案，进而按照上述流程开展评价。

4.3 遗传操作

作业调度瓶颈因素往往存在于资源利用率较高的时段，而利用率低时段的工序仍有充分利用资源以提升作业效率的潜质，故将资源利用率作为一项启发性因子，以引导遗传进化中的交叉变异操作。

定义5基准保障方案S在t时刻的加权综合资源利用率为

(16)

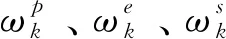
4.4 自适应变邻域局部搜索

除遗传操作外，还引入局部搜索机制(邻域变换)，引导优有个体在适应度函数的极值处作深度探索。该搜索机制，一是利于种群个体跳出局部最优解，二是根据当前状态调整邻域结构加快搜索[24-25]。针对优先数编码设计了5类不同规模的邻域结构：

1) 交换邻域：随机交换不存在前后续结束工序的编码所对应基因位的优先数。

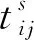
3) 项目内活动灾变邻域：随机选取机群中舰载机i，再随机取出其中Na(Na∈Z[4,9])个工序，对每个工序按照插入邻域依次重新插入。

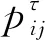
(17)

式中：width为衡量抽样概率的延展参数，算法取值为width=1。

5) 项目重组邻域：随机选取机群中舰载机i，对其所属所有工序按流程进行随机插入，即重组其时序优先数。

根据邻域规模来划分，交换邻域和插入邻域属于小规模邻域结构，项目内活动灾变邻域和局部时间活动灾变邻域属于中规模邻域结构，项目重组邻域输入大规模邻域结构。

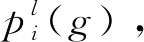
(18)

(19)

式(19)为第g次局部搜索选中第i个邻域结构进行操作后的概率更新公式，式(19)为未选中邻域结构的概率更新公式，αreward、αpenalty分别为奖励学习和惩罚学习速率，Nl为邻域结构数，β(g)为第g次迭代所获得的回报反馈，不妨取：

(20)

从而确保当邻域结构在进化过程有改进效果时，其选择概率会相应增加。

4.5 阈值评估机制

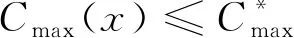
(21)

F(x1)

(22)

(23)

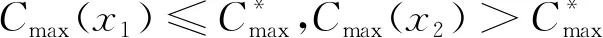
5 仿真实验

5.1 场景设置

甲板作业保障仿真场景如图1所示，机队调度为多个单机作业的综合，单机调度的项目流图及作业工序参见文献[23]中图、表的资源覆盖数据。各类保障工序在人员主观因素、保障对象状态、设施设备保障条件等客观因素综合作用下，保障时间所服从的分布规律不尽相同。在作业交互数据合理假定下通过AnyLogic仿真软件模拟测试，作业工时的概率分布主要包括：截断正态分布、均匀分布和二项分布。其中，工时服从二项分布的保障工序主要包括充氧和充氮，并非每次飞行前准备都需要实施，而是根据一定概率进行保障，其本质即为实验次数为1的伯努利试验，事件发生概率为p。

表3 保障工序时间随机分布参数

5.2 确定性保障调度仿真及算法对比

经多次实验比对，将设计的I-Memetic算法参数设置为：种群规模NP=30，标准变异概率Pm=0.1，局部搜索的循环邻域操作次数下界，上界，学习自动机的奖励学习速率和惩罚学习速率分别为αreward=0.8、αpenalty=0.8。标准GA算法中，采用二元锦标赛选择、两点交叉和随机变异操作，其中变异概率取Pm=0.05，LA-VNS算法参数的设置与上述I-Memetic算法一致，其它算法的参数则参照所引用文献的参数设置。算法取最大调度次数作为终止条件，在1个场景下进行1次完整的机群保障作业仿真，即为1次调度。

将上述8种算法在不同调度次数下分别进行30次独立运行，得到的结果如表4所示，其中Q为调度次数。

表4 算法性能对比

对比表4的数据，可以看出：① 所提出的I-Memetic算法相对其它算法有了更进一步的提升，无论在各调度次数等级下，算法的最优解搜索能力和算法稳定性均优于其它所列算法；② 通过标准GA算法的仿真结果对比，说明本文I-Memetic算法可有效克服传统标准GA算法的缺陷，避免限入局部最优解或导致提前收敛，从而可有效挖掘适应度函数空间，且验证了所采用的双种群迭代机制具有良好的可拓展性；③ 在LA-VNS算法的仿真结果对比，说明提出的基于学习自动机的变邻域搜索算法不仅局部搜索能力良好，同时具有较强的全局搜索性能，优于标准GA、MDE、Memetic和SAHGA等算法。

5.3 鲁棒调度策略与算法对比

在所设计的机群保障案例下，考虑工序保障时间随机不确定下的前摄性鲁棒调度优化仿真，主要包括2部分，一是基于本文设计的I-Memetic算法，对比CPC、接力赛、时刻表、CRB和CAB等5类调度策略，在不同鲁棒人员分配和设备调整执行模式和不同调度次数下的鲁棒性指标；二是对比本文I-Memetic算法、DSaDEII算法与求解经典资源受限随机项目调度问题的ABGA(Artifical Beecolony Genetic Algonthm)算法[29]、果蝇算法(Order-based Fruit fly Optimization Algorithm, OFOA)[30]用于求解ACDCO-PRS的鲁棒性效果。

在人员、设备鲁棒调度分配对比分析中，设置I-Memetic算法参数与5.2节相同，鲁棒指标权重ω=0.1，优化过程抽样场景NS=20，所有仿真结果均基于30次独立运行得出。

首先，对不同调度策略、不同鲁棒人员分配与设备调整执行模式和不同调度次数下的鲁棒调度优化进行对比，得到仿真结果如表5所示。其中鲁棒人员分配和鲁棒设备调整可选择执行(是)或不执行(否)，当不执行鲁棒设备调整时，按照基于串行调度机制所生成的初始设备分配方案执行保障；当不执行鲁棒人员分配时，则按照累积保障时间最少优先规则进行分配；由于CRB策略和CAB策略是面向任务列表，因此不涉及人员和设备分配方案。表中结果[abc]分别表示机群按时完工概率、完工时间期望和完工时间方差。

同时，基于CPC策略，鲁棒人员分配和设备调整均执行，调度次数为Q=250 000下得到的最优基准方案，分别采用4类调度策略进行场景抽样数为3 000次的蒙特卡洛仿真，所得保障完工时间分布的箱线图如图6所示，其中横轴为表5中的CPC、接力赛(Roadrunner)、时刻表(Railway)及CAB等调度策略，纵轴为保障完工时间(min)。

表5 调度策略性能对比

又取最优基准方案中的时序方案，分别在不同鲁棒人员分配和设备调整执行模式下进行场景抽样数为3 000次的蒙特卡洛仿真，所得保障完工时间分布的箱线图如图7所示。其中的1、2、3、4编号的箱线图分别代表鲁棒人员分配和设备调整均有，随机人员分配而有鲁棒设备调整，有鲁棒人员分配而无鲁棒设备调整以及鲁棒人员分配和设备调整均无等4类组合。

通过表5、图6基于不同调度策略的鲁棒性目标仿真结果，图7对有无鲁棒人员/设备分配情况下完工时间的对比实验，可知：

图6 不同调度策略下保障完工时间箱线图

图7 不同鲁棒性分配组合下保障完工时间箱线图

1) 在给定鲁棒人员分配和设备调整模式下，从整体鲁棒性指标看来，调度策略的排序为CPC>时刻表>接力赛>CAB>CRB。时刻表策略由于限制了开工时间，一定程度上减少了开工时间波动性，因此其完工时间的方差较小；接力赛策略对所有工序采用并行调度，破坏了基准调度方案中供给性资源保障计划的积极进度特性，从而劣化了解的鲁棒性能；同样，基于并行调度机制的CRB策略对基准调度方案的积极进度特性的破坏则是全方面的，因此所得结果较差。

2) 鲁棒人员分配和鲁棒设备调整机制均对基准调度方案的鲁棒性指标有提升作用，且前者的作用相对后者作用更为明显。这主要是由于工序保障对人员的需求远高于对设备的需求，且设备主要是一对一需求，即1架飞机对某类设备可能仅有1道工序有需求，一对多需求的以电站为主，因此可供鲁棒性设备调整的对象并不多，而鲁棒人员分配则面向所有工序集合，影响范围更广。

为验证I-Memetic算法有效性，将其与求解资源受限随机项目调度问题的代表性算法进行对比，包括ABGA和OFOA。不同最大调度次数下的最优解的鲁棒性指标和平均鲁棒性指标统计如表6所示。其中，DSaDEII算法除了算法框架与I-Memetic算法不同，其内涵均与I-Memetic算法相一致，包括鲁棒人员分配和设备调整机制，CPC调度策略，基于蒙特卡洛仿真的阈值评估机制等。在调度策略上，ABGA采用CAB策略，OFOA采用CRB策略。

表6 鲁棒调度优化算法对比

6 结论与展望

在对工时具有随机不确定性假设下，针对机队保障应最大可能在甲板作业周期内完成，提出前摄性鲁棒调度和预约束策略，运用I-Memetic算法结合Monte Carlo仿真验证了鲁棒基准调度的可行性、算法的有效性。

图8 保障人员分配甘特图

2) Monte Carlo对鲁棒优化的基准调度方案仿真表明，方案能较好地适应人员、设备工时扰动影响。

3) 提出的I-Memetic算法显著优于已有智能优化算法，预约束策略好于接力赛、时刻表等鲁棒调度策略。

由于对RCPSP的资源分类过细致，使模型复杂、约束耦合多、求解困难，下步可考虑采用调度分解方式开展同类资源归并的分层规划、甲板分区保障的并行调度研究，从而降低问题复杂度，由任务规划算法重构RCPSP网络流图，采用Cplex约束规划器求解。也可使用强化学习方法，结合专家知识开展包括但不限于工时不确定条件下动态调度。此外，对工时不确定性还可考虑凸多面体等处理办法，引入其它可调节鲁棒性指标开展基于优化器精确解法的调度研究。