基于嵌套网格变几何轴对称进气道非定常数值模拟

罗炯，李志宏，陈科，向欢

航空工业成都飞机设计研究所，成都 610091

随着飞行器速度不断提高，未来飞行器飞行范围得到了极大扩展，速域覆盖从低速、超声速到高超声速，对动力提出了更高的要求，任何单一动力形式都无法满足从低速到高超声速的宽速域工作需求，涡轮/冲压组合动力是最有希望满足这一需求的动力形式。进气道作为推进系统的关键部件，其性能对飞行器性能有至关重要的影响，必须在宽马赫数范围内稳定工作，另外还要求：总压损失小、出口流场均匀、工作稳定、抗干扰能力强、阻力小等[1]。这就对进气道宽速域设计提出了巨大挑战。

如何使进气道在宽速域范围内保持良好的工作状态，一直是组合动力高速飞行器的设计难点，国内外对此开展了很多研究。常用的方法是针对固定几何进气道设计抽吸、溢流[2]，尽量降低进气道起动马赫数，但这种方法效果有限，并不能提高总体性能，甚至可能增加飞行器溢流阻力。此外，更有效的方法是，通过变几何调节，改善进气道起动性能，使进气道能更好地兼顾设计点及非设计点的性能。在各种压缩形式的变几何进气道中，轴对称进气道利用中心锥和唇罩内表面对来流进行压缩，具有压缩效率高、流场畸变较低等优点，多年来一直受到国内外众多研究机构和学者的关注，并在高速飞机和导弹上得到了广泛应用。

20世纪60—70年代，美国针对变几何轴对称进气道进行了深入研究。洛马公司研制的“黑鸟”SR-71高空高速战略侦察机(图1)采用中心锥可前后移动的轴对称进气道方案[3]，巡航马赫数可达3.2。美国马里兰大学的Colville等就以SR-71轴对称进气道为基础，用CFD的方法研究了多种改变几何外形的方法及其效果，包括转动外罩唇角度、中心锥锥角改变等[4-6]。NASA德莱顿飞行研究中心提出了一种在中心锥上开槽(图2)的方法来拓宽轴对称进气道工作范围[7]，在非设计点状态时，中心锥上的槽道打开，增加喉道的面积，适应低速流量需要，并用F-15飞机挂载进行了进气道飞行验证。日本ISAS的研究人员为串联TBCC发动机ATREX设计了变几何轴对称进气道，在法国ONERA的超声速风洞完成了变几何自动调节试验[8]。东京大学的Kobayashi等还发明了一种中心体由一个顶锥和多个圆盘组成的的多级盘式轴对称进气道[9]，进气道中心锥上圆锥盘之间的距离的改变使得中心锥长度随之改变，从而控制进气道的流量系数和总压恢复系数。国内南京航空航天大学对于变几何进气道研究也有较多进展，滕建等设计了一种中心锥带凹腔的变几何轴对称进气道，后退圆锥头部可提高流量系数[10]；李建用设计点马赫数6.0的轴对称进气道数值模拟发现，中心锥向前移动时，不但可以提高低马赫数下气动性能，还可以改善起动性能[11]。

图1 黑鸟SR-71飞机

图2 中心锥变体进气道

真实飞行过程中，在进气道几何调节和来流扰动的共同影响下，进气道流场具有强烈的非定常特征，而这种非定常流动极容易造成进气道的不起动。Wagner等在风洞试验中采用转动进气道出口斜板的方式实现出口反压的变化，分析了反压变化引起的进气道不起动的流场结构[12]。国防科技大学的游进通过数值模拟和试验相结合的方法对混压式进气道再起动特性及调节方法的机理和相关影响因素进行了研究[13]。南京航空航天大学的刘凯礼等对迎角动态变化的二元进气道进行了非定常数值模拟，进气道特性有明显迟滞现象，低速区非定常效应影响显著[14]；王卫星等采用非定常数值方法研究了高超声速进气道自起动过程中非定常流动特性，分析了流道外形及来流对进气道自起动过程中流动特性影响[15]。

目前对于进气道数值模特的研究一般采用传统的定常模拟方法，向欢等采用嵌套网格非定常方法对战斗机大迎角时进气道气动特性进行了数值模拟[16]，该文中进气道外形不变，而进气道变几何调节过程涉及到进气道外形的变化，非定常数值模拟研究有待进一步加强。

本文对可调轴对称进气道，使用嵌套网格技术数值模拟中心锥前后动态调节非定常过程，同时在调节过程改变来流条件和进气道出口反压条件，讨论了中心锥动态调节过程中流场变化规律和进气道性能变化规律，研究了轴对称进气道调节的非定常过程在临界反压下中心锥移动速度对进气道起动性能的影响，为进气道方案设计和改进提供参考。

1 物理模型及计算方法

设计点马赫数为3.5的单级轴对称混压式进气道的二维模型图如图3所示。它由一个轴对称的中心锥和外罩组成，其半锥角角度为13.5°，内收缩比为2.60。当来流马赫数发生变化，中心锥体也会相应地前后移动。计算马赫数为2.5～3.5，飞行高度11 km，攻角0°。不同马赫数Ma之间的中心体移动规律如图4所示。从马赫数2.5～3.5，中心锥一共后移400 mm。锥面激波不断后退，激波角不断减小。在每个马赫数变化的区间内，假定中心锥的位移随马赫数线性变化。

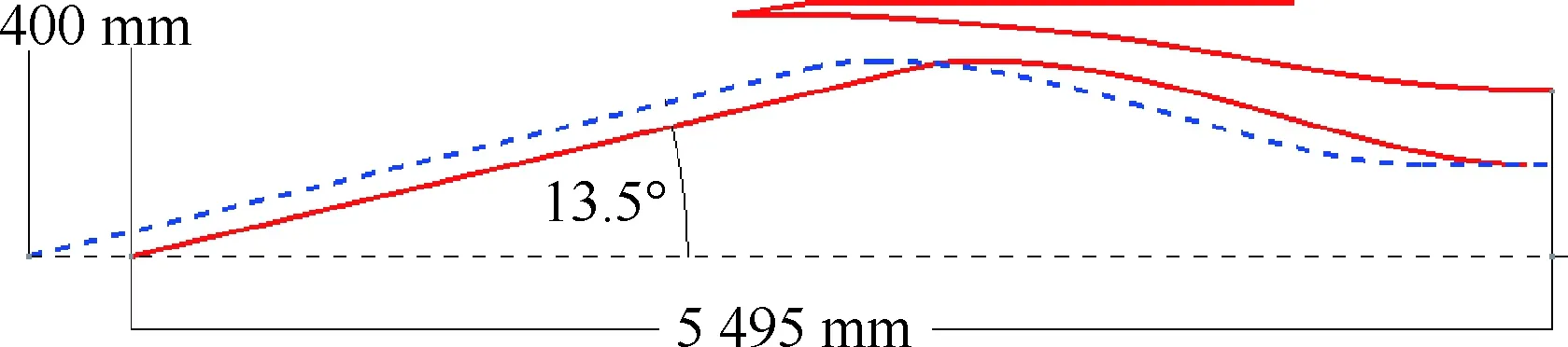
图3 轴对称进气道方案

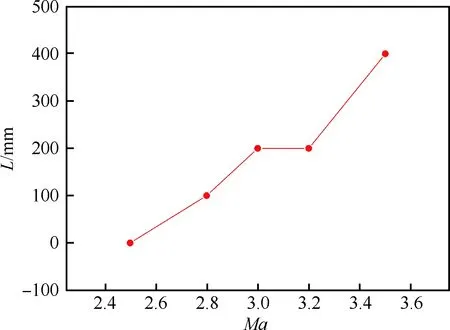
图4 中心锥移动变化规律

本文所用计算软件是Metacomp Technologies公司的CFD++，该软件基于有限体积法求解RANS方程，软件可计算结构化或非结构化网格，拥有MPI并行计算能力，其中无黏项是2阶TVD格式，黏性项采用中心离散格式，湍流模型采用Realizablek-ε模型。对于定常状态，初始流场为来流条件，此时整个流场的流动参数都和来流一样。当出口流量不再变化时，认为得到稳态结果。非定常计算采用URANS方法，初始流场为初始时间的稳态流场，采用隐式LU-SGS时间推进方法，通过引入子迭代即双时间步使得时间方向上达到较高的精度，总时间步设置为0.5 ms，其中子迭代设置10步即可让子迭代内残差能够下降3个数量级。嵌套过程如图5～图8所示，其中背景网格数为16万，嵌套网格数为3万。嵌套网格会把背景网格中多余的部分切割下来，得到我们想要的完整网格。进气道模型生成的非结构网格如图7所示。网格总数为5万，物面第1层网格厚度为0.012 mm。进气道内部网格适当加密，以便能解析更真实流动状态。远场边界为3.0 m，避免计算过程激波的影响。在模拟中心锥的移动时，使用了CFD++中嵌套网格技术。将中心锥用网格包裹，嵌套入背景网格之中，当中心锥移动时，包裹中心锥的嵌套网格整体移动即可。

图5 定常计算网格

图6 背景网格

图7 嵌套网格

图8 非定常计算网格

本文先对典型马赫数工况进行了定常模拟，通过逐步增加反压，研究了典型马赫数下进气道的抗反压能力。然后对进气道动态调节过程进行了非定常模拟，研究了进气道动态调节时的流场变化规律。

2 定常状态计算分析

图9给出了设计状态Ma=3.5在不同进气道出口反压Pb下马赫数分布和密度梯度的模分布云图，其中密度梯度的模清晰地反映了流场的激波结构。正激波被推出之前，锥面激波基本封住了唇口，流量系数接近100%，随着不断增加出口反压，正激波最终被推出。表1给出了流量系数和总压恢复系数随反压的变化情况，定常状态计算下，进气道出口反压增大到43.5P∞(P∞为远场来流压力)时进气道仍然处于起动状态，超过此反压进气道将不起动，此时进气道处于临界状态。进气道进入不起动状态后，进气道出口的流量系数和总压系数均出现大幅降低。反压较小时，结尾激波处在进气道喉道后的扩张段，此时结尾激波前马赫数较高，总压损失较大；随着反压增大，结尾激波移动到喉道处，波前马赫数降低，结尾激波损失较小，进气道总压恢复系数得到提高。

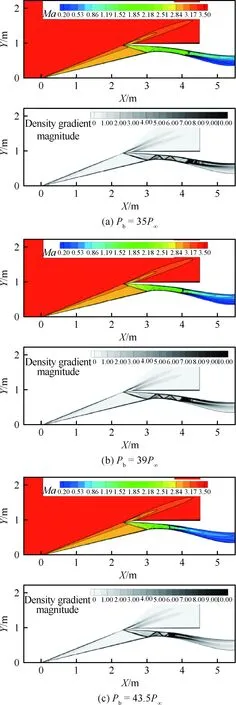
图9 Ma=3.5不同反压下进气道出口流场结构

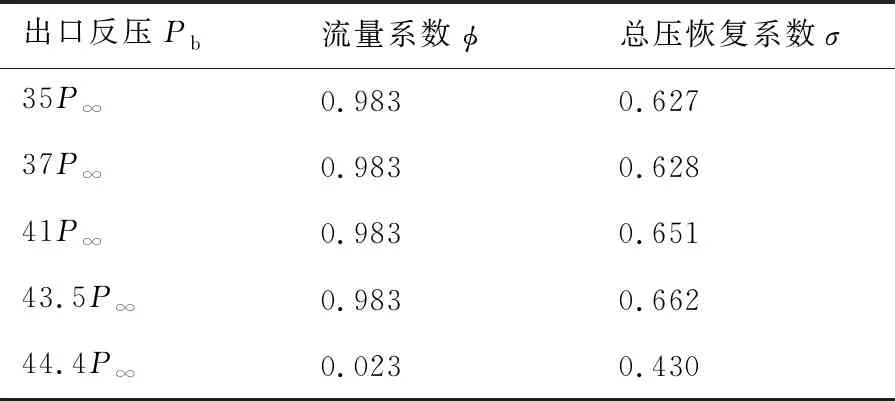
表1 Ma=3.5时进气道性能

图10给出了Ma=2.5～3.2工作状态进气道马赫数分布和密度梯度的模分布云图。随着马赫数的增加，第1道斜激波不断增强，气流进入进气道后经过多道斜激波增压减速，在进气道喉道后形成一道末激波将气流减速到亚声速。表2给出了各个马赫数的起动状态进气道工作状态时进气道出口反压、流量系数和总压恢复系数。随着马赫数增加，中心锥不断后移，锥面斜激波角减小，到设计状态马赫数3.5形成封口，流量系数也随之增加。由于马赫数3.0～3.2中心锥没有移动，故马赫数3.2下总压恢复系数偏小，马赫数3.2～3.5中心锥向后移动了200 mm，内收缩比增大，大幅改善了设计点马赫数3.5总压恢复系数。

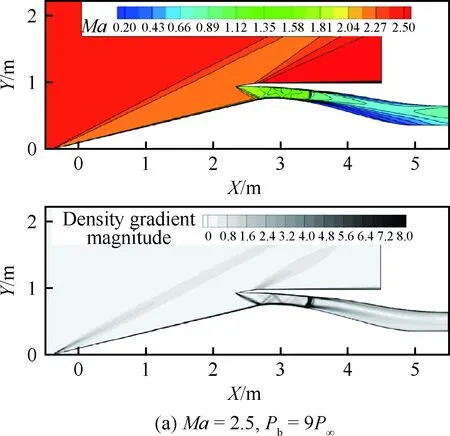
图10 Ma=2.5～3.2工作范围进气道流场

表2 不同来流调节进气道性能

3 非定常状态计算分析

根据进气道的设计，当马赫数从2.5增加到2.8，中心锥后移D=100 mm，进气道出口反压会从9P∞增加到14.7P∞，图11～图12给出了计算来流马赫数随时间变化及出口反压随时间变化，两者均为线性变化，通过非定常方法数值模拟此动态过程。分别用1 s总时间来实现这一过程，研究非定常的流场变化情况。初始时刻t=0 s时流场为Ma=2.5时定常计算得到的稳态流场。

图11 来流马赫数随时间变化

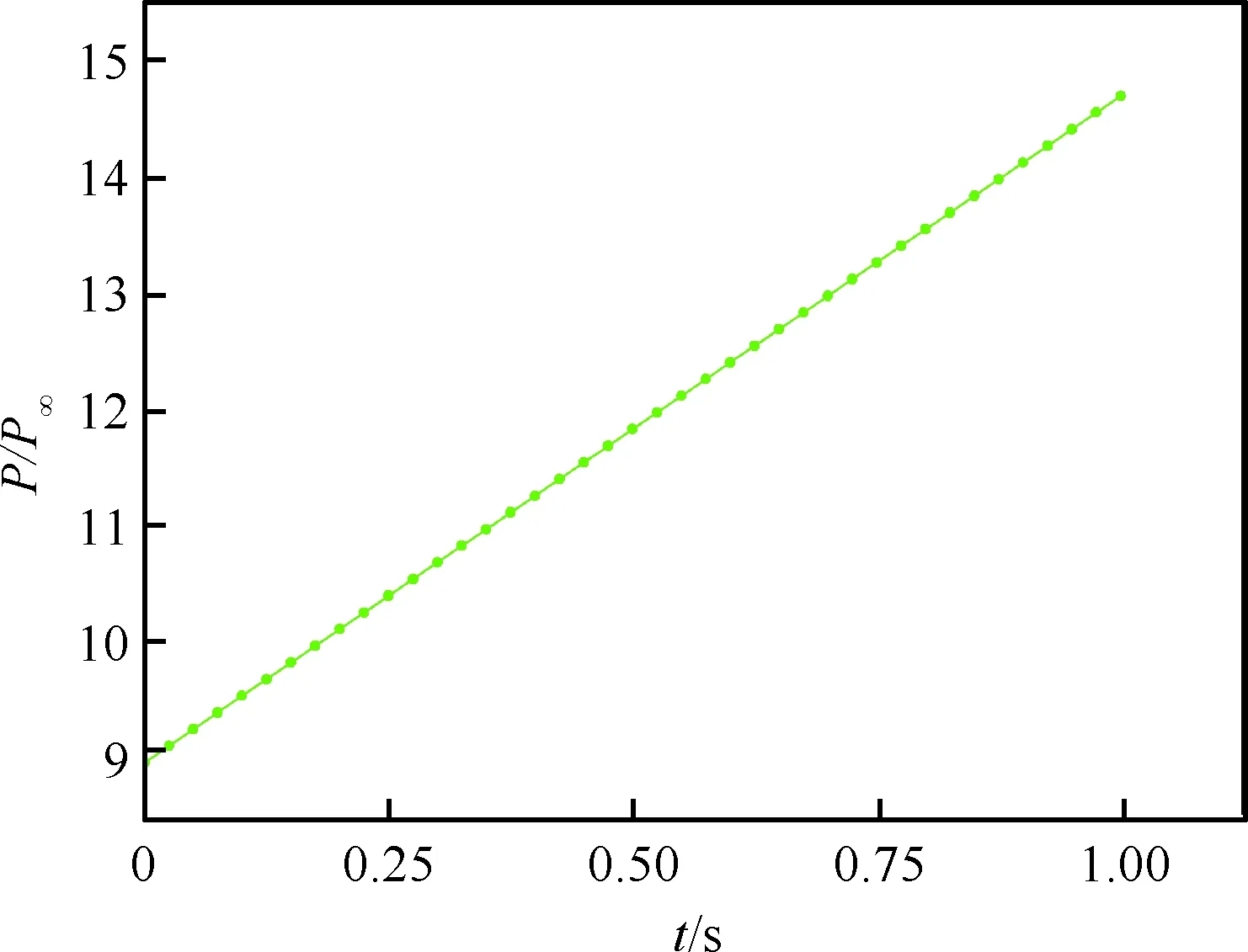
图12 进气道出口反压随时间变化

图13给出非定常计算结果各个时刻的马赫数云图分布，图14给出了非定常计算各个时刻流场激波结构变化情况。中心锥移动过程中，来流马赫数不断增加，锥面激波逐渐向唇口移动，唇口反射激波不断增强，唇口到喉道处形成了激波串，将流体进一步增压减速，结尾激波保持在喉道附近，进气道保持起动状态。图15～图16给出了进气道流量系数及总压恢复系数随时间变化规律，流量系数基本随时间线性增加，总压恢复系数基本随时间线性减小。表3给出了计算结束时刻进气道出口流量系数和总压恢复系数与定常状态对比，相比于定常状态，非定常计算结果得到的流量系数降低了0.019，总压恢复系数降低了0.015。

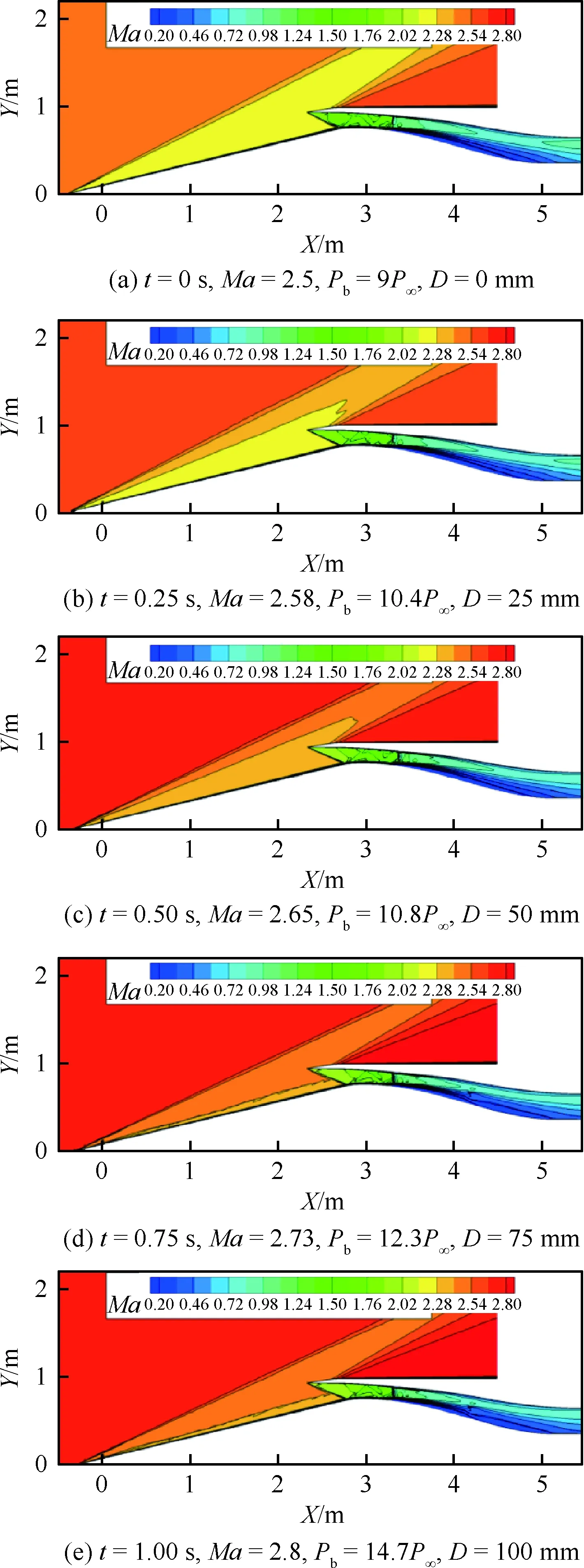
图13 不同时刻马赫数云图分布(Ma=2.5～2.8)

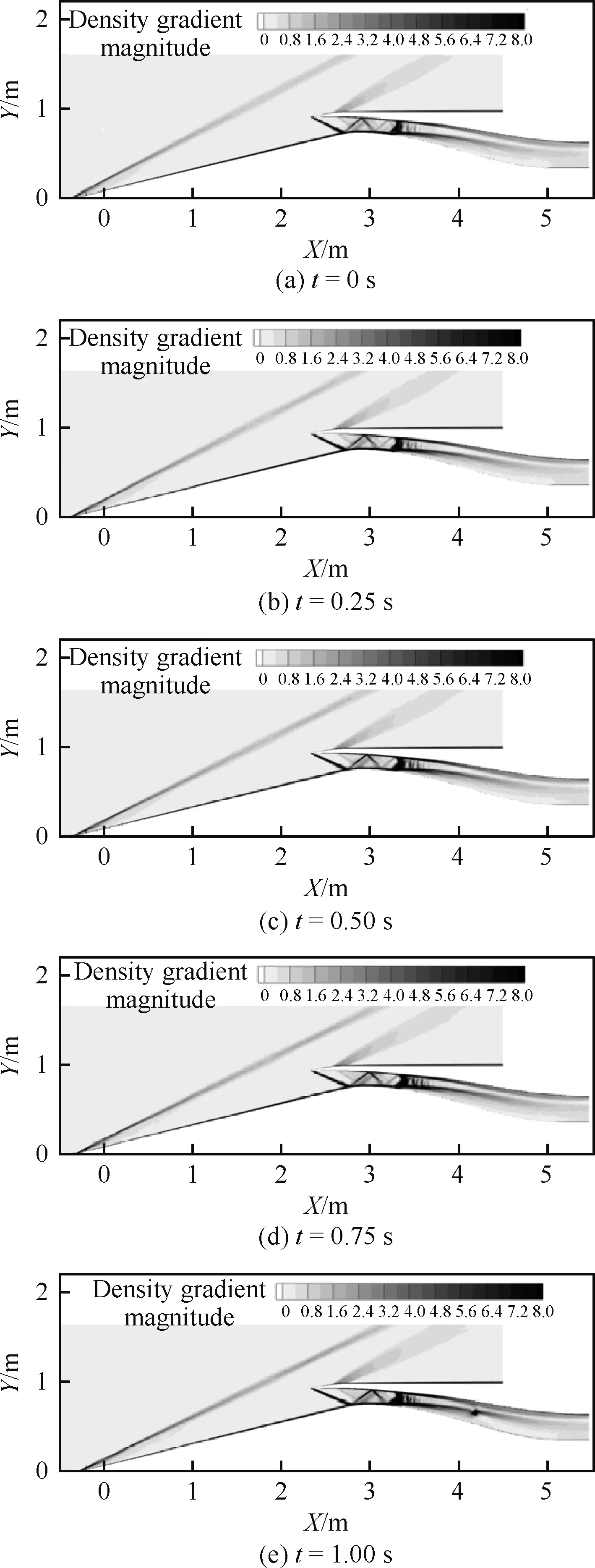
图14 不同时刻流场激波结构(Ma=2.5～2.8)

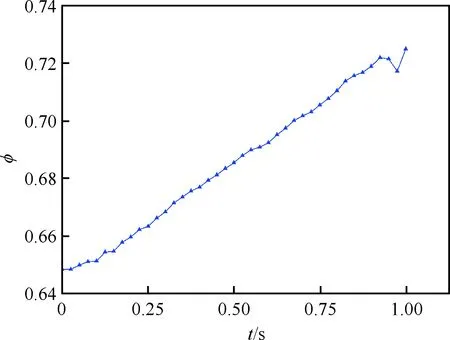
图15 进气道流量系数随时间变化

图16 进气道总压恢复系数随时间变化

表3 动态调节时进气道性能变化(Ma=2.8)

考虑中心锥不移动，来流条件从马赫数3.0增加到3.2，进气道出口反压从21P∞增加到25P∞，假定来流马赫数和反压随时间线性增加，通过非定常方法数值模拟此动态过程。整个过程耗时1 s，初始时刻t=0 s流场为Ma=3.0时定常计算得到稳态流场。图17给出了非定常计算得到马赫数云图分布在各个时刻变化，随着来流马赫数增大，锥面激波逐渐靠近唇口，唇口激波前马赫数不断增大，唇口激波强度增加，结尾激波小幅向后移动，基本保持在喉道附近，进气道处于起动状态。表4给出了马赫数为3.2时，定常状态和非定常状态计算得到进气道性能，流量系数变化不大而总压恢复系数下降0.01。

图17 不同时刻马赫数云图分布(Ma=3.0～3.2)

表4 动态调节时进气道性能变化(Ma=3.2)

4 结 论

通过CFD数值模拟分析了某款混压式轴对称进气道在典型工况的抗反压能力和设计点基本性能，之后又通过非定常方法模拟了进气道在典型工况点间动态调节的过程中流场变化和进气道性能变化规律，得到了以下结论：

1) 在同一来流马赫数下，随着进气道出口反压的提高，进气道内结尾激波向喉道移动，波前马赫数降低，激波损失减小，总压恢复系数得到提高，当进气道出口反压超过一定值后，结尾激波被推出进气道内，整个进气道处于不起动状态。

2) 非定常数值模拟中心锥移动过程，在马赫数2.5～2.8过程中，中心锥向后移动了100 mm，锥面激波逐渐向唇口靠近，唇口激波逐渐增强，结尾激波基本保持在喉道附近，进气道处于起动状态。

3) 非定常计算和定常计算结果对比可知，进气道受到动态过程小扰动影响性能略微下降。