高超声速飞行器前缘主动冷却影响因素

罗世彬，庙智超，宋佳文

中南大学 航空航天学院，长沙 410083

热防护技术是高超声速飞行器的关键技术之一，随着飞行速度的进一步提升，热防护问题成为制约高超声速飞行器发展的核心所在[1-2]。热防护技术根据其冷却原理的不同，可分为被动和主动式热防护。航天飞机、宇宙飞船等再入式高超声速飞行器由于所受气动加热严重，峰值热流密度过高等限制，大都采用了结构简单、技术成熟的烧蚀冷却[3]。未来世界各国为降低空间运输成本，大力发展可重复使用天地往返飞行器，对于整个飞行任务中气动外形的保持提出了更高的要求[4]。单纯依靠一次性使用、成本过高的烧蚀冷却难以满足任务需求[5]，因此需要探索能抵抗更高热流密度、可长时间工作、可重复使用、温度和热流可闭环控制的热防护技术[6]。

主动冷却是一种通过自身携带或从外界获取冷却工质与壁面进行热交换带走热量或形成气膜覆盖在高温壁面表面阻止热量传递的冷却方式[7-8]。其中，气膜冷却和发散冷却相较于对流冷却有更高的冷却效率和更少的冷却剂消耗量，已在航空发动机的涡轮叶片和端壁冷却中得到了广泛应用[9]。针对高超声速应用背景下，气膜冷却可极大降低鼻锥壁面的热载荷[10]，但需要较大的吹风比，不利于长时间工作。此外，Ding等[11]指出，采用单一气膜冷却时，大量的冷却剂热沉未得到合理利用。针对高超声速飞行器发散冷却技术，近年来研究表明[12]，由于前缘结构具有曲面效应，曲面附近驻点区域的温度和压力过大，远大于前缘的下游直线段，导致多孔介质内的冷却剂分布不均匀，在热流密度最高的头部区域反而冷却剂质量相对更少，在主流温度较高的情况下，可能会导致多孔介质烧蚀，发散冷却失效，影响飞行器的正常工作。由于气膜冷却和发散冷却在高超声速应用背景下都存在自己的优势和局限性，通过结构设计，可将气膜冷却和发散冷却进行组合，实现优势互补[13]。清华大学的Huang等[14-15]设计了支板发散-气膜组合冷却结构，并通过实验和数值模拟验证该结构可显著提升冷却效率。中国科学技术大学的Ding等[11]提出了一种双层气膜-发散组合冷却结构，研究了3种质量流量下，不同内层气膜孔的数量对结构整体冷却效率的影响，并对组合冷却结构的流动换热机理进行了研究。

当前针对鼻锥、前缘发散冷却研究集中在对结构的优化、冷却剂种类以及多孔介质参数的研究中[11]。Zhao[16-17]和林佳[18]等分别开展了基于多孔鼻锥模型的液态水发散冷却试验和气态发散冷却数值模拟，选取了主流参数中的温度、速度、雷诺数，研究其对多孔鼻锥冷却特性的影响。Ding等[11, 19]提出前缘间断发散冷却模型和前缘双层气膜-发散冷却模型，通过研究不同的结构布局来分析冷却特性的改变，而关于运行工况只研究了不同的冷却剂流量的影响。

目前关于鼻锥、前缘的发散冷却采用的计算工况和真实飞行工况存在一定差别，在研究中为了简化模型选取了0°攻角。但是高超声速飞行器在实际飞行过程中，攻角会实时发生变化，此时飞行器体轴不再与速度方向平行，来流的特性会发生极大的改变，对前缘主动冷却的影响也更加明显。关于前缘半径和热流密度的关系已知，但关于前缘楔角的改变给前缘组合冷却带来的影响目前尚无研究。此外，前人的研究中所采用的几何模型均为上下面对称结构，考虑到真实飞行器的前缘外形在设计时可能会采用上下非对称结构，因此有必要对非对称构型前缘的组合冷却效果进行研究。本文在Ding等[11]提出的具有良好冷却效果的气膜-发散组合冷却结构基础上，针对来流攻角、前缘楔角产生的非对称因素对前缘主动冷却结构的影响进行研究，揭示流动换热规律，为高超声速飞行器主动冷却结构设计提供参考。

1 数值模拟

1.1 物理模型

采用的物理模型参考了Ding等[11]提出的高超声速飞行器前缘双层气膜-发散组合冷却结构，结构示意图如图1所示。其中，内部为空腔，尾部管路用于输送冷却剂。内层为开有离散槽缝的结构金属层，采用高强度铝合金材料制成，可增强组合冷却结构的承载能力；外层为基于多孔介质的发散冷却层，采用镍基高温合金粉末烧结而成。

图1 高超声速飞行器前缘组合冷却结构[11]

为了减小计算的复杂度，将三维模型简化为二维模型进行研究，简化模型如图2所示[11]。前缘总长度L为 40 mm，上楔角为θ1，下楔角为θ2，头部半径为3 mm，多孔介质和高强铝合金厚度均为1 mm，离散槽缝及气膜孔的宽度均为0.5 mm。以前缘头部最前端为平面直角坐标系的原点，将X轴坐标由前缘总长度L进行无量纲化处理。

图2 模型尺寸示意图[11]

1.2 数学模型和数值方法

本文建立了包括主流通道、多孔介质、固体、冷却剂通道4个计算域。主流通道和冷却剂通道计算域的控制方程如下：

(1)

(2)

(3)

式中[20-21]:ρ为流体密度,kg/m3；U为流体速度,m/s；p为压力,Pa;τ为剪切应力,N；E为内能,J；λ为热导率,W/(m·K)；T为温度，K。

由于多孔介质真实结构复杂，内部孔隙形状及大小各不相同，在数值模拟时一般不采用直接模拟的手段，而是对其进行简化，通过在动量方程中添加源项来模拟流动阻力，源项由黏性损失项和惯性损失项组成。基于Darcy定律的Forchheimer-Brinkman修正方程已被广泛用于描述多孔介质内的流动特性[22]，其特点是同时考虑了流体流动惯性和黏性耗散影响，可用于多孔介质区域动量方程的建立。多孔介质传热模型主要有局部热平衡模型(Local Thermal Equilibrium, LTE)和局部非热平衡模型(Local Thermal Non-Equilibrium, LTNE)，区分这两种模型的依据是多孔介质内部固体相温度Ts和流体相温度Tf是否相等。当多孔介质内部固体相与流体相之间的换热充分时，可视为两相温度相同，此时可采用局部热平衡模型。研究表明，局部热平衡模型相对于局部非热平衡模型的计算工作量大大减少，并广泛用于研究多孔介质内流动换热。因此多孔介质区域的能量方程采用了热平衡模型进行分析[23]。综上，多孔介质单相发散冷却控制方程为

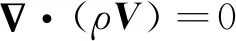
(4)

(5)

(6)

(7)

λeff=ελf+(1-ε)λs

(8)

式中:ε为多孔介质孔隙率；V=εU为Darcy速度,m/s；μ为流体动力黏度,Pa·s；K为多孔介质渗透率；dp为颗粒直径,m；λeff、λf和λs分别为多孔介质有效导热系数、流体导热系数和固体导热系数[20-21]。

固体计算域的热传导方程为

(9)

由于本文求解的是高超声速可压缩流动，因此选用密度基求解器和隐式求解算法。采用二阶迎风格式对控制方程的对流项进行离散化；采用组分输运模型并设置混合物为空气和氮气，空气密度采用理想气体模型，黏度采用萨瑟兰定律，热导率和比热随温度变化的数据从NIST数据库中获取并进行多项式拟合。引入多孔介质热平衡假设，并开启多孔介质局部热平衡模型，冷却剂在多孔介质内视为层流流动，多孔介质参数参考Shen等[24]的多孔介质前缘试验件，孔隙率设定为0.33，渗透率为7.5×10-14m2。多孔介质骨架材料选取高温合金Inconel-600[25]，热物性参数如表1所示[25]。

表1 高温合金Inconel-600热物性[25]

采用SSTk-ω湍流模型针对图3中的超燃冲压发动机支板发散冷却进行模拟，提取收敛后的结果与Xiong等[26]的结果进行对比，如图4所示。可以看出，采用SSTk-ω模型得到的支板外壁面温度曲线与文献中变化趋势一致，且吻合程度较好。此外，与本文前期的工作中研究对象一致[27]，计算方法的准确性也曾得到过验证，证明该方法用于本文的研究是合理的。

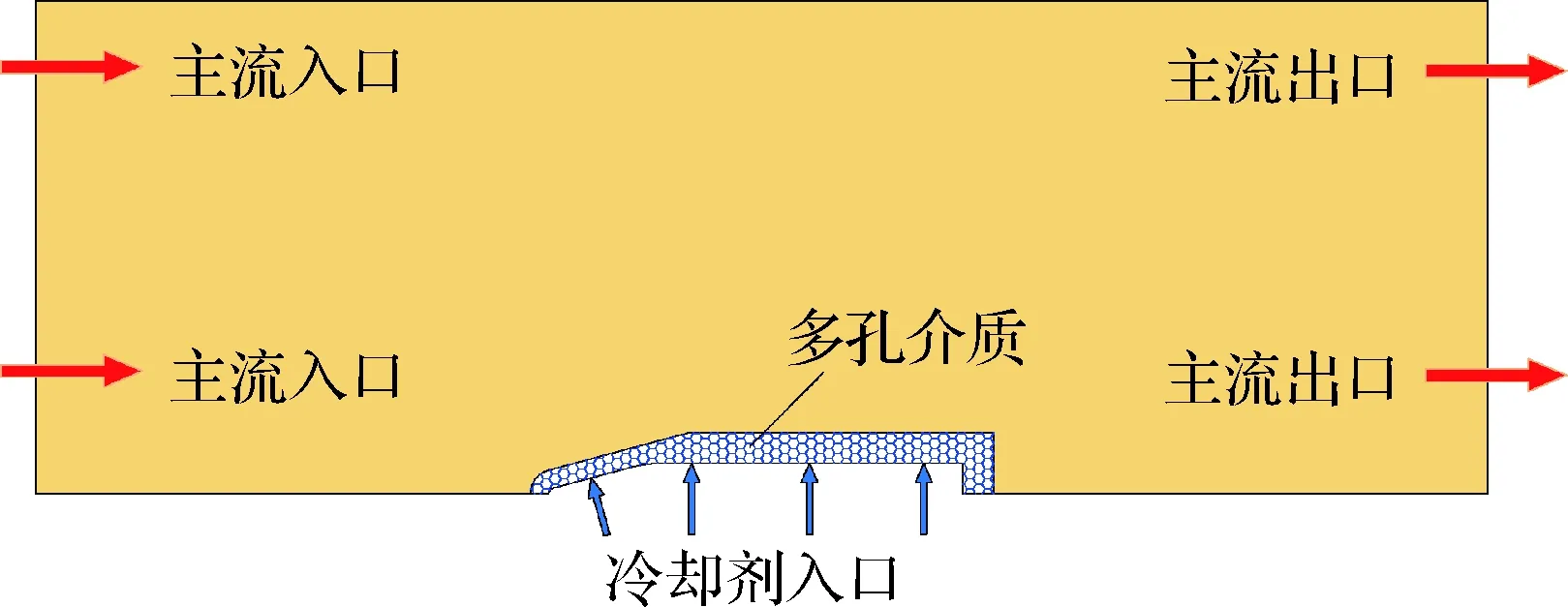
图3 超燃冲压发动机支板发散冷却示意图[26]

图4 数值模型验证结果

1.3 网格划分与边界条件

采用O型和Y型分块技术对计算域进行结构化网格划分，由于SSTk-ω模型对无量纲壁面距离Y+值要求较高，通常需满足Y+值小于1。通过流体速度、密度、动力黏度、边界层长度可计算出第1层网格高度，并对前缘外表面进行加密。最终生成的网格如图5所示，在整个计算域内质量大于0.93，越靠近1代表网格质量越高。控制第1层网格高度不变，分别生成4套不同节点数的网格用于网格无关性验证，从网格1～网格4沿着主流的流向进行加密，且网格的节点数按照1.5～2的倍数递增。给定主流工况：来流马赫数4.2，攻角为0°，总压1.33 MPa，总温2 310 K，前缘外壁面为绝热壁面。0°攻角下可选取模型的一半来计算无冷却情况下的驻点温度。

图6给出了用4种网格计算出的前缘正前方的温度曲线。从网格2开始，误差百分比都低于0.1%，可以看出由网格引起的误差对结果的影响很小，为了降低计算的开销，提高计算效率，这里选取网格2用于后续的计算。网格2的半模网格量为120 597，全模网格量为241 194。

图5 结构化网格示意图

图6 不同网格量下前缘正前方温度分布

主流入口采用压力远场边界条件，在研究来流攻角、前缘楔角影响时，工况和Shen等[24]的高超声速发散冷却试验工况一致，来流马赫数4.2，总压1.33 MPa，总温2 310 K。冷却剂入口设置为质量流量入口，质量流量为0.03 kg/s，入口压力为0.18 MPa，冷却剂为N2。主流、冷却剂、固体与多孔介质计算域之间的传热耦合采用直接整场离散策略进行求解，主流出口设置为压力出口边界。

2 结果分析

2.1 来流攻角对组合冷却效果的影响

改变来流攻角α为0°、4°和12°，其他边界条件不变，分析攻角对组合冷却效果的影响。图7为不同攻角下的全场温度云图，从图中可以看出，随着攻角的增大，激波的形成位置不再是前缘正前方，而是沿着逆时针方向转动，因此流场结构不再对称，迎风面受到来自主流的流动冲击加强，迎风面的气动加热情况更严重，温度明显低于背风面的温度。通过对比3种工况，发现攻角的变化对多孔介质和结构金属层内温度分布有较大的影响。

图8为沿X方向的多孔介质外壁面温度变化曲线。首先，几种攻角下的温度变化趋势一致，X/L=0～0.33区间为温度快速变化段，X/L=0.33～1为温度缓慢变化段。其次，攻角改变使多孔介质上下壁面出现了较大的温差，α=4°时上下壁面温差达到639.2 K，α=12°时温差达到459.2 K。从图中可以看出，从α=0°～4°时，峰值温度增大了4.2%，而从α=0°～12°时峰值温度增大了32.8%，且峰值温度所在坐标也向下游移动。从图8中还可看出，在所有的温度曲线中，α=12°时下壁面的峰值温度为全局最高温度，达到1 587.3 K，虽然此时尚未超过多孔介质骨架材料Inconel-600的熔点，若以较长时间保持12°攻角飞行，随着热量的积累，有可能会导致多孔介质局部温度过高，影响发散冷却的效果。针对此种情形，可以增大冷却剂的质量流量以及采用更高熔点的材料作为多孔介质的骨架。

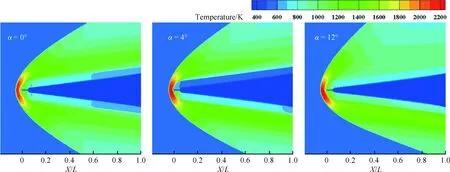
图7 不同攻角下全场温度云图

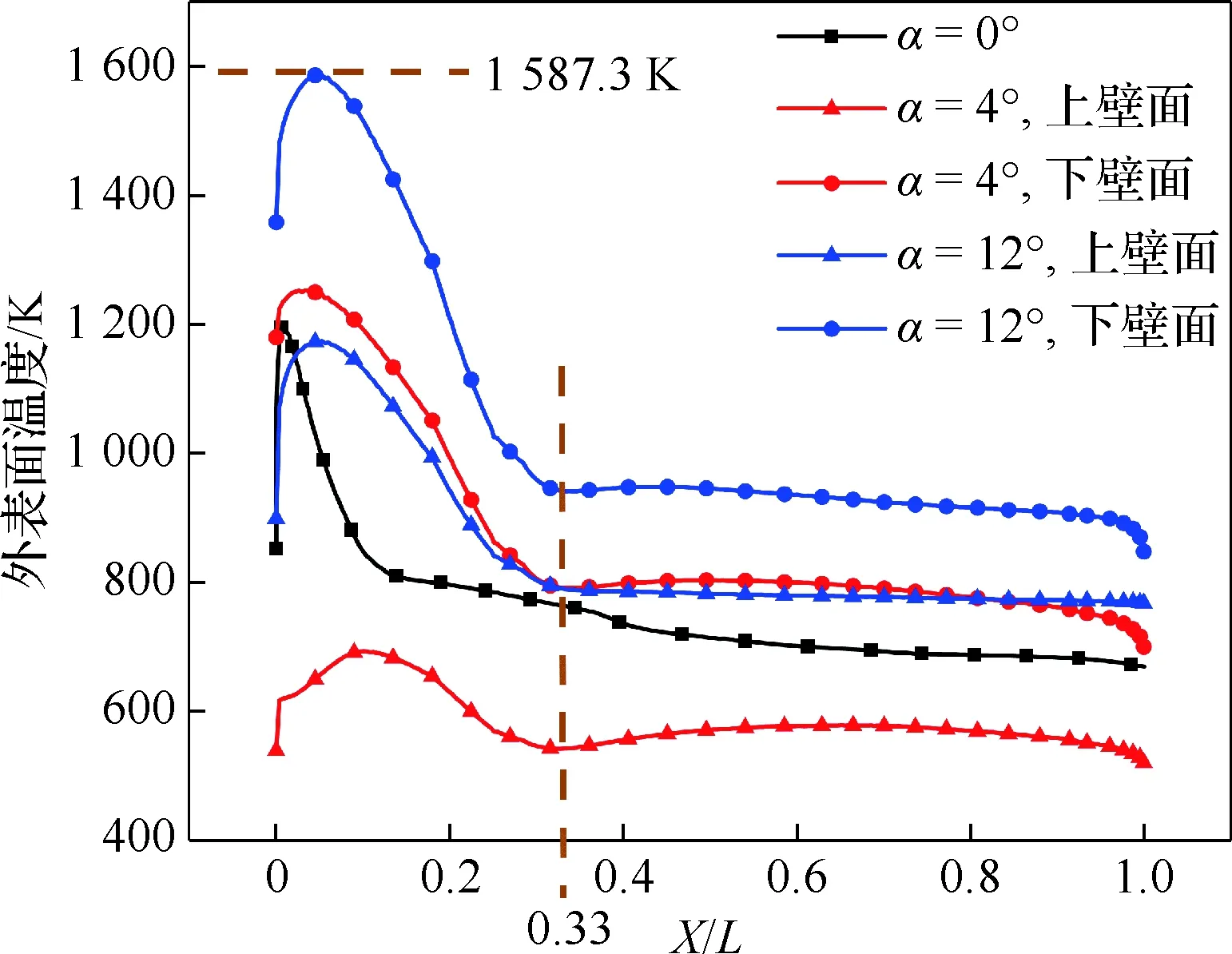
图8 不同攻角下外壁面温度沿X方向变化

图9为沿X方向的多孔介质外壁面压力变化曲线，图10为α=0°，4°，12°时的全场压力云图及流线图。从图10中可看出，当α=4°，12°时，多孔介质外壁面的压力分布不均匀，且下壁面的压力要明显大于上壁面的压力。在α=0°时，压力的最大值出现在气膜孔出口区域，而随着攻角的增大，头部高压区域也沿着多孔介质表面逆时针转动，导致冷却剂更难从多孔介质下表面中流出，发散冷却的效果较差，因此下表面的温度明显高于上表面。

图9 不同攻角下外壁面压力沿X方向变化

图11为α=0°，4°，12°时的冷却剂质量分数云图。从图中可以看出，冷却剂从右边入口注入后，一部分会从前端的气膜孔流出，在主流的作用下形成气膜，对头部区域进行覆盖；另一部分冷却剂通过结构金属层之间的离散槽缝进入到多孔介质内，冷却剂主要集中在X/L=0～0.15段，从图7和图8可知此区间是前缘承受气动力热最严重的区域，均匀分布的离散槽缝发挥了合理分配冷却剂的作用。X/L=0.15～1段外表面压力明显减小，一部分冷却剂会在压力的驱动下向下游扩散。当α=0°时，多孔介质上半段和下半段冷却剂质量分数一致，α=4°，12°时，多孔介质上半段内冷却剂的质量分数要远大于下半段。当α=4°时，多孔介质上半段内冷却剂质量分数明显大于其他两种工况，且冷却剂附面层脱离壁面的距离较小，多数附着在上壁面。

因此α=4°时，气膜冷却和发散冷却对上壁面的冷却作用明显。此外，通过冷却剂在主流中的分布可以看出，当攻角增大到12°时，从气膜孔喷出的冷却剂不易附着在表面，更多的冷却剂耗散在主流中，这也导致了在α=12°时前缘头部的温度较高，与图8中的现象一致。

2.2 非对称构型前缘组合冷却效果分析

控制前缘下楔角θ2=9°，改变上楔角分别为θ1=0°，3°，5°，研究当前缘截面为非对称构型时，对组合冷却效果的影响。

图12为不同上楔角的全场温度云图，从图中可以看出，前缘外流场特征相似，这是因为在改变楔角的过程中，头部半径保持不变。而楔角的增大使得多孔介质内整体温度增大，并引起多孔介质内温度梯度分布发生改变。

图13为θ1=0°，3°，5°时，多孔介质外壁面的温度分布情况。从图中可以看出，在整个外壁面，温度曲线变化趋势一致，并且峰值温度所在坐标一致。随着上楔角的增大，前缘头部的峰值温度有较小幅度的增加，壁面最高温度可达1 339.8 K。在不同的工况中，多孔介质下壁面温度都始终大于上壁面温度，θ1= 0°，3°，5°时，上下壁面最大温差分别为148.9 K、110.4 K和93.5 K，随着构型越接近于对称，上下壁面的温差越小。

图14通过提取θ1= 0°、 5°的壁面温度数据进行插值得到θ1= 3°时的插值温度，并与θ1= 3°的实际壁面温度进行对比。从图中可以看出，θ1= 3°时实际壁面温度的数据点基本都落在插值温度曲线上或其上方，上壁面实际温度与插值温度之间的平均误差为2.6%，下壁面实际温度与插值温度之间的平均误差为2.0%。因此可知上下壁面的温度都随楔角呈现近似线性变化。

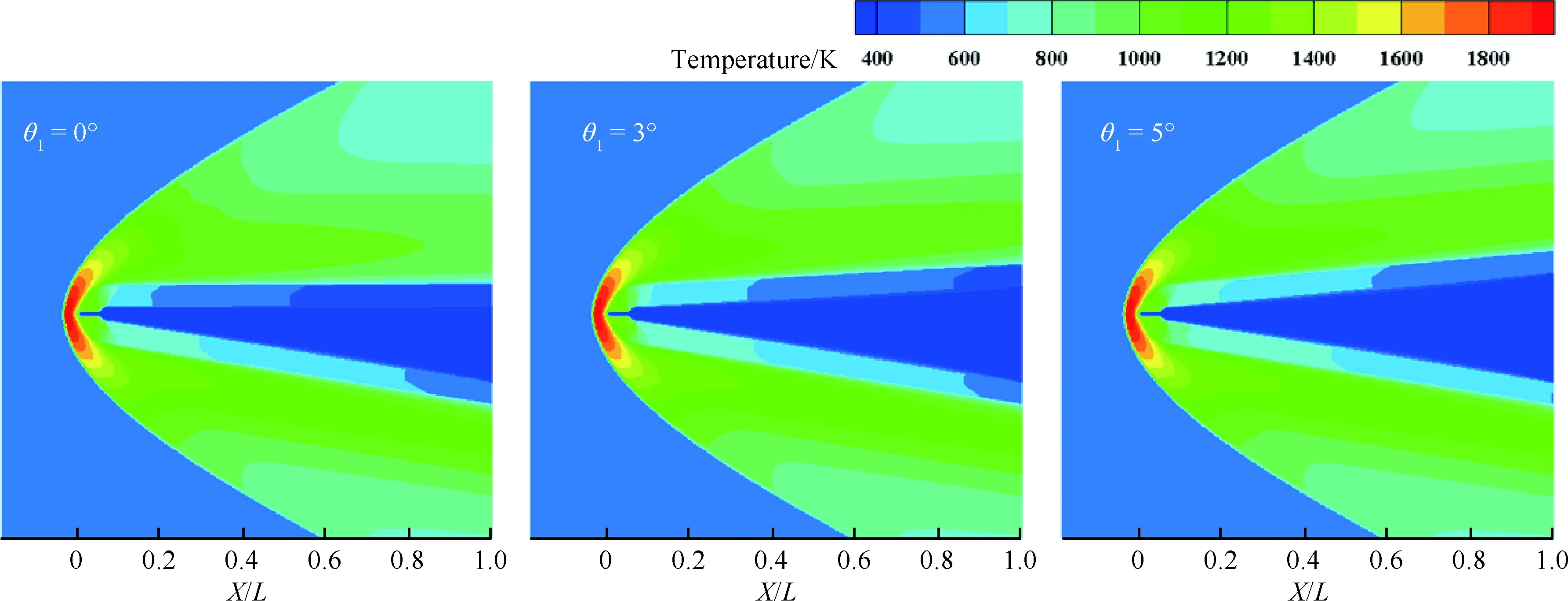
图12 不同上楔角下全场温度云图

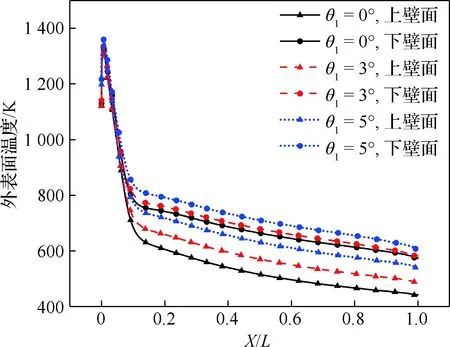
图13 不同上楔角下外壁面温度沿X方向变化

图14 上楔角3°时插值温度与实际温度对比

图15为θ1=0°，3°，5°时的冷却剂质量分数云图。从图中可以看出，当上楔角增大时，冷却剂在多孔介质内向下游扩散距离减小，而多孔介质下半部分冷却剂质量分数几乎不受上楔角变化的影响。此外可以看到θ1=0°时，前缘上半段的第1个槽缝出口处的冷却剂质量分数明显小于θ1=3°和θ1=5°。

图16为θ1=0°，3°，5°时，计算域内压力云图和流线图。从图中可以看出当θ1=0°时，多孔介质上半段的离散槽缝出口的压力值较小，未能和周围的环境形成压力梯度，从流线可以看出在槽缝入口处有明显的回流现象，因此冷却剂很难从该槽缝注入多孔介质中，这也验证了为什么图15中该处冷却剂质量分数明显小于其他两种工况。冷却剂从前端的气膜孔中喷出过程中会有一部分直接进入到多孔介质中换热后流出表面，可以看到楔角越小时，冷却剂通过此方式注入到多孔介质内的质量越多，冷却剂会向下游的低压区扩散，提高下游的冷却效果。

图17为θ1=0°，3°，5°时，多孔介质外壁面的压力分布情况。从图中可以看出，不同楔角情况下，压力曲线变化趋势一致，下壁面压力几乎不变，这是因为下楔角始终为θ2=9°，前缘下半部分外流场结构未受到影响。在X/L=0～0.077区间，上壁面的压力相近，而在X/L=0.077～1区间，上壁面的压力随楔角增加小幅度增大。

图15 不同上楔角下冷却剂质量分数云图

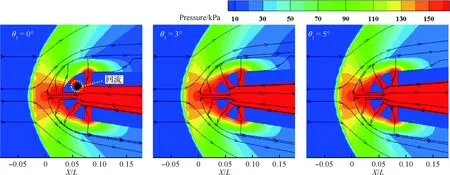
图16 不同上楔角下压力云图和流线图

图17 不同上楔角下外壁面压力沿X方向变化

3 结 论

本文以高超声速飞行器前缘组合冷却结构为研究对象，通过数值模拟的方法，分析了不同的来流攻角对组合冷却效果的影响。通过改变前缘的上楔角来研究非对称构型下组合冷却的流动换热规律。主要的结论如下：

1) 不同的攻角对前缘周围流场的影响较大，流场特征不再对称，由此带来前缘外壁面的压力和温度的改变。压力的大小决定了冷却剂从多孔介质中流出到外表面形成气膜的难易程度和冷却剂在多孔介质中的输运能力。

2) 当攻角为4°时，上下壁面的温差达到了639.2 K，攻角为12°时，最高温度可达1 587.3 K，局部温度过高对热防护结构带来了巨大的考验，在极端工况中，需要对结构进行进一步优化设计，或考虑进一步加大冷却剂流量以及采用更加耐热的骨架材料等。

3) 当前缘截面构型不再对称时，上楔角的改变影响了多孔介质内部的温度分布，随着上楔角的增大，冷却剂向多孔介质上半段的下游输运距离减小。通过数据的对比发现外壁面的温度随楔角增大呈现近似线性增长的规律。

4) 当楔角为0°时，在多孔介质上半段的离散槽缝入口处出现了明显的回流现象，冷却剂很难从此槽缝进入到多孔介质中。

点阵结构是多孔结构的一种，有优良的力学性能以及换热能力，目前的增材制造加工技术已较为成熟，相对于采用粉末冶金技术烧结而成的多孔介质材料具有更多的发挥空间。下一步可将点阵结构引入到高超声速飞行器前缘发散冷却结构设计中，研究不同的点阵单元类型、单元尺寸以及点阵设计尺寸等参数对冷却效果的影响。