单级冲击采样器切割头气流特性及切割粒径研究

吴政江 彭小勇 陈丽园

南华大学土木工程学院

0 引言

惯性冲击采样器是一种测量空气中颗粒物浓度的装置。切割头是采样器内部非常重要的构件，作用为进行细颗粒物的分级和采样。2006 年，国内学者刘运席等[1]设计出七级不同粒径范围的颗粒物采样器，并增加了旋转收集功能，使得颗粒物收集更加均匀，填补了国内采样器研究领域的空白。2013 年孙奇等[2]通过研究撞击效率与无量纲数之间的关系，发现常规撞击采样器对高温颗粒的粘附效果更好。

为研究切割头喷嘴伸入空腔内对切割效率的影响，本文建立了喷嘴处不同的两种结构模型，通过分析切割器内部流场和无量纲数曲线来探究喷嘴处结构对捕捉效率的影响机理。

1 物理模型及数值方法

图1 给出了单级冲击采样器切割头物理模型，其中图1（a）为模型1（喷嘴末端平齐模型外壁），具体尺寸为：空气入口直径4 mm，空气入口渐缩段小口直径2 mm，管长16 mm，喷嘴到冲击板的距离为6 mm，捕捉面直径为10 mm，冲击板直径为15 mm，外壁直径18 mm，空气出口处直径10 mm，长度12 mm。图1（b）为模型2（喷嘴末端向下延伸），模型二尺寸与模型一基本相同，喷嘴处有所差异，喷嘴向下延伸2 mm。

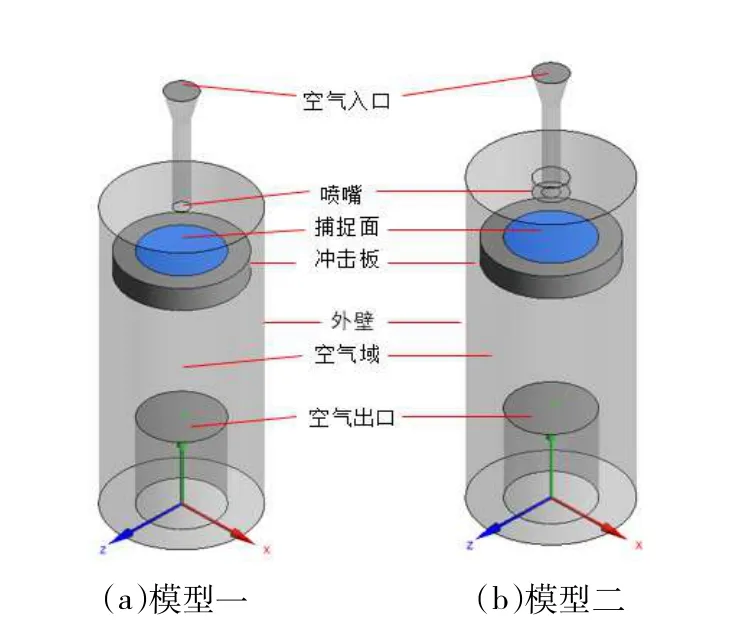
图1 冲击采样器切割头物理模型

采样器内部空气流动满足低速不可压缩湍流流动，湍流模型采用标准κ-ε 模型。采用离散项模型（DPM）对颗粒物运动进行模拟。采用稳态压力基求解器，速度与压力基的耦合选用SIMPLE 算法，动量、能量和湍动能均采用一阶迎风的差分格式进行离散。单级冲击采样器切割头边界条件设置见表1，其中冲击板上有捕捉面用于捕捉颗粒物，其表面较为粗糙，在实际使用时会均匀涂抹凡士林来防止颗粒物反混，故捕捉面DPM 项设为Trap。为得到较准确的计算结果及较快的收敛速度，对喷嘴、捕捉面及冲击板周围进行局部加密，所有网格都采用六面体结构化网格，并采用O 型网格划分方式。网格数量约为80 W，质量均在0.65 以上。

表1 边界条件设置

2 模拟结果及分析

2.1 切割头流场分析

在模型中心进行XOY 面切片，对入口速度为7 m/s 的速度流线图进行分析，如图2。空气离开喷嘴后贴近冲击板壁面流动，两模型在捕捉面附近的速度流线无明显差异。

图2 速度流线图及局部放大图

为进一步分析，分别在模型一、模型二XOY 平面取三条观测线段（X 取值为（-1.5，1.5），见图4）：分别位于捕捉面上方0.85 mm、0.45 mm、0.05 mm 处。观测线2 位于捕捉面往上0.45 mm 处、观测线3 位于捕捉面往上0.05 mm 处。每条线段长3 mm，分等距取31 个点绘制速度曲线图。观测线位置见图3，观测线速度曲线见图4。

图3 观测线示意图

由图4 可知，随着高度的减小，在靠近捕捉面的位置，模型二中心处的速度比模型一小，随坐标位置的向外移动两个模型速度均有所增大，且模型二增速更快，在与喷嘴管径相同坐标位置的时候，即X=-1 mm 和X=1 mm 处，两个模型速度相同。而后，坐标越远离中心位置，模型二外侧速度大于模型一，且差值逐渐增大。模型二曲线曲率较大，速度改变较快，根据惯性撞击原理，颗粒物不易克服惯性改变运动轨迹从而撞击在捕捉面上，因此模型二对于颗粒物捕捉效果更好。

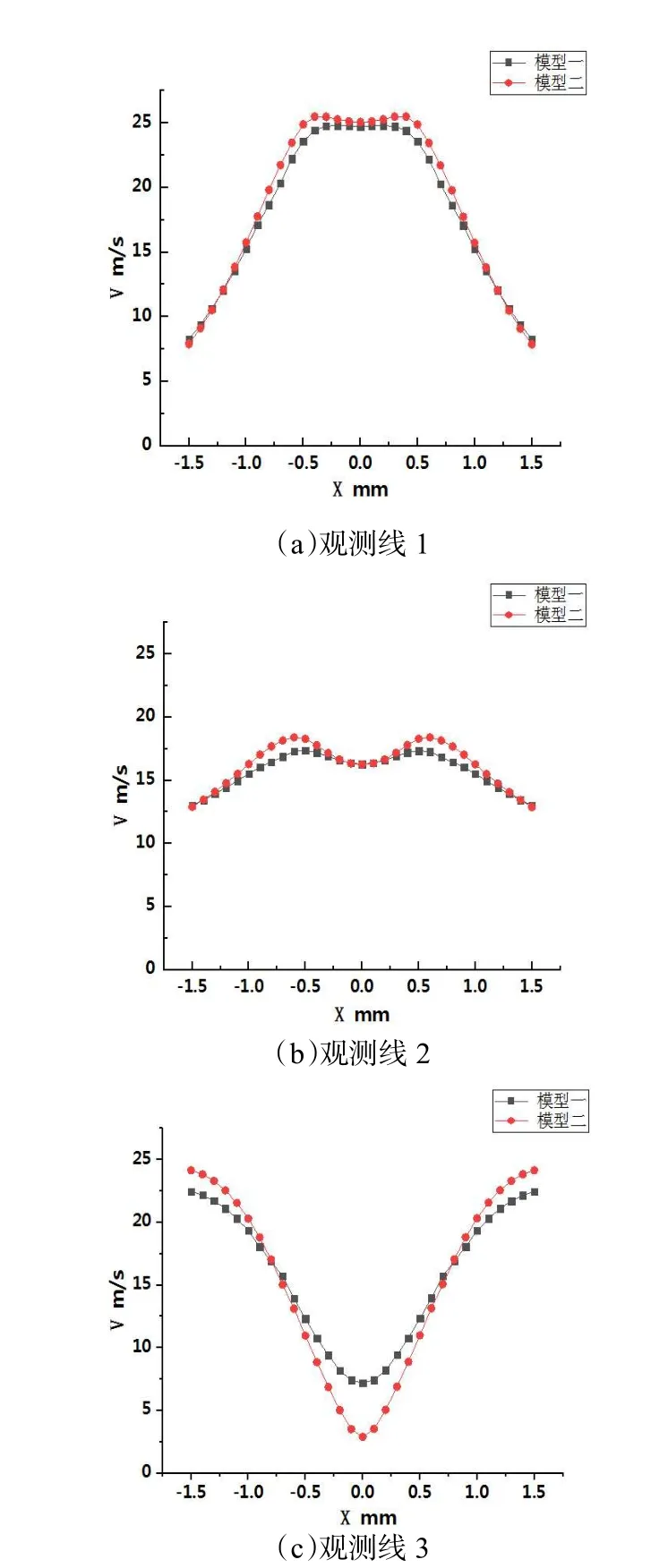
图4 观测线速度曲线图

2.2 颗粒物轨迹分析

设粒径为0.5 μm、1 μm、1.5 μm、2 μm、2.5 μm、3 μm、3.5 μm、4 μm、4.5 μm、5 μm 十种球形惰性颗粒物，其密度均为1000 kg/m3。在DPM 数值计算时，考虑曳力和重力作用。

入口速度为7m/s 时，对粒径为1.5 μm、1 μm、1.5 μm、2 μm 四种颗粒物的运动轨迹进行研究，每种粒径颗粒物在入口处分别释放200 个，由图5 可知，粒径为1 μm 颗粒物大约有50 个绕过冲击板从出口处流出，粒径为1.5 μm 的颗粒物大约有10 个绕过冲击板，而粒径为2 μm 及2.5 μm 的颗粒物全部捕捉面捕捉；由图6 可知，粒径为1 μm 和1.5 μm 的颗粒物几乎都可以绕过冲击板，而粒径为2 μm 的颗粒物约有50 个绕过冲击板从出口流出，粒径为2.5 μm 的颗粒物全部捕捉面捕捉。模型一对粒径为1.5 μm、1 μm、1.5 μm、2 μm 四种颗粒物的捕捉率较高，但由于粒径1 μm、1.5 μm 的小颗粒物逃逸率较低，反而导致其切割效果不佳，无法有效通过粒径对颗粒物进行区分。而模型二对粒径1.5 μm 和2 μm 的颗粒物捕捉效果差异较大，可以有效地通过粒径对颗粒物进行选择性捕捉。

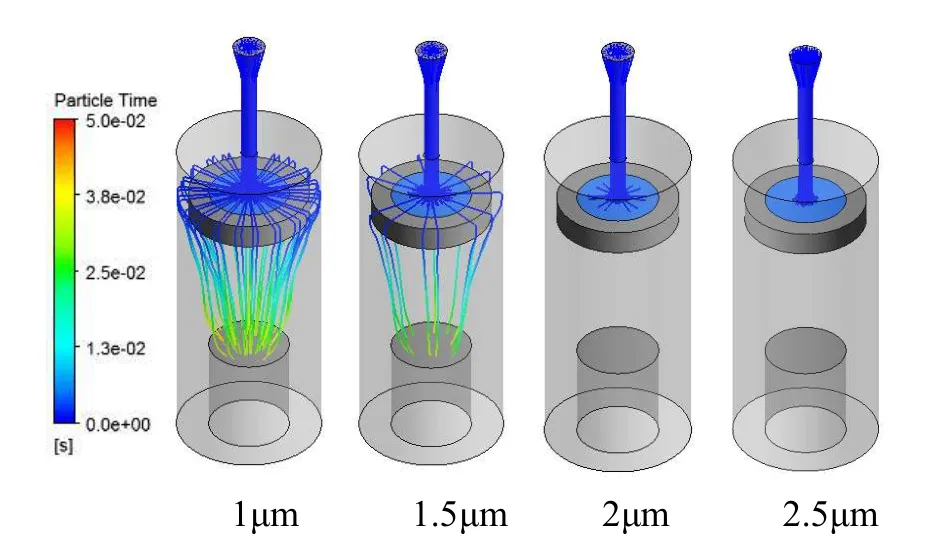
图5 模型一在V=7 m/s 时的颗粒物轨迹图

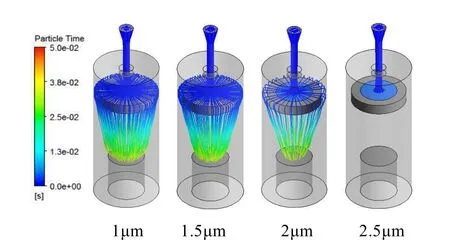
图6 模型二在V=7 m/s 时的颗粒物轨迹图

无量纲数Stoke 数[3]是用来描述惯性采样器切割头颗粒物动力学行为，表征捕捉率的重要参数之一，它也常被用于描述颗粒物离开流线难易程度。为更好的研究两个模型在切割颗粒物时的区别，引入对两个模型切割效果进行评价

选取粒径1 μm 至3.5 μm，入口速度0.6 m/s、1 m/s、2 m/s、4 m/s 的颗粒物，计算出，并选取作为横坐标，捕捉率（冲击面上被捕捉的颗粒物总数与速度入口颗粒物总数之比）为纵坐标，见图7。

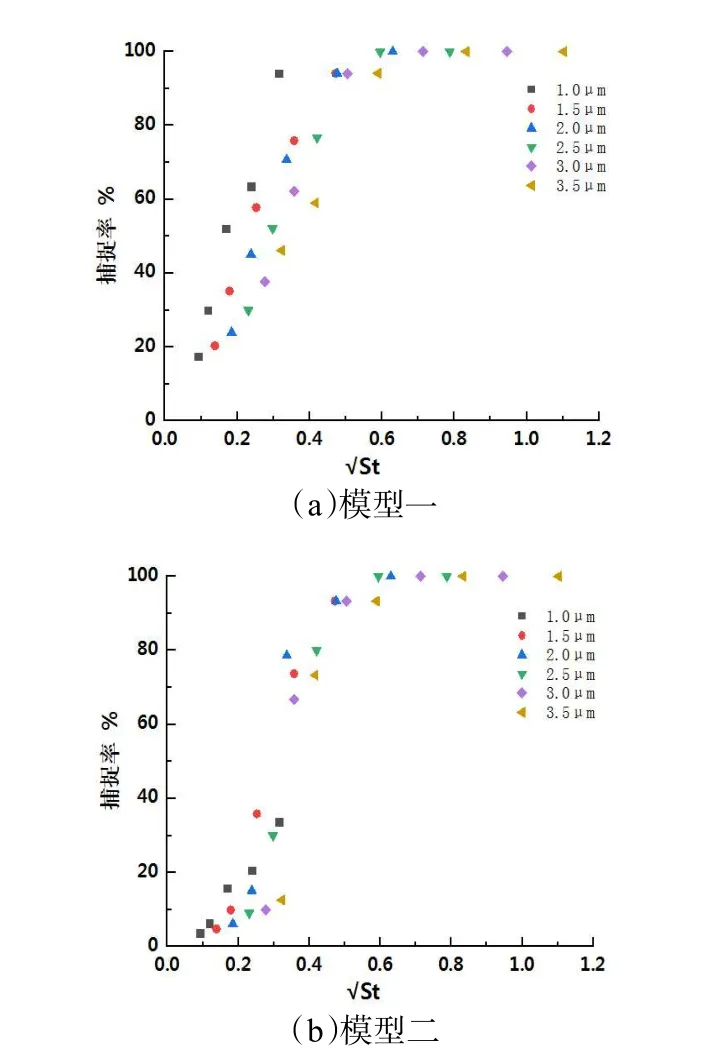
图7 数与捕捉率散点图

2.4 颗粒物粒径与捕捉率分析

选取粒径0.5 μm 至5 μm 的颗粒物（密度ρp=1000 kg/m3），当入口速度为0.6 m/s、1 m/s、2 m/s、4 m/s、7 m/s 时，颗粒物捕捉率随粒径变化曲线见图8。由图8 可见，入口速度为V=0.6 m/s 时，模型一和模型二切割头对粒径4 μm 以下的颗粒物几乎没有捕捉作用。而入口速度为V=7 m/s 时，模型一和模型二切割头对粒径2.5 μm 以上的颗粒物几乎全部捕捉，没有区分效果。从其他曲线也可以得出结论，入口速度较大时对应的切割粒径较小，入口速度较小时对应的切割粒径较大。

通过对图8 曲线对比发现，模型一切割头捕捉率曲线较为平坦，如入口速度为4 m/s 时，切割头对颗粒物捕捉率从20%升至100%的粒径范围是0.5 μm 至3.5 μm，相对应的模型二切割头入口速度为4 m/s 时，捕捉率0%升至100%所对应的粒径范围是1.5 μm 至3.5 μm，曲线较模型一更为陡峭。因此，可以看出在模型二切割头捕捉率比模型一更陡峭，对颗粒物的切割效果更好。

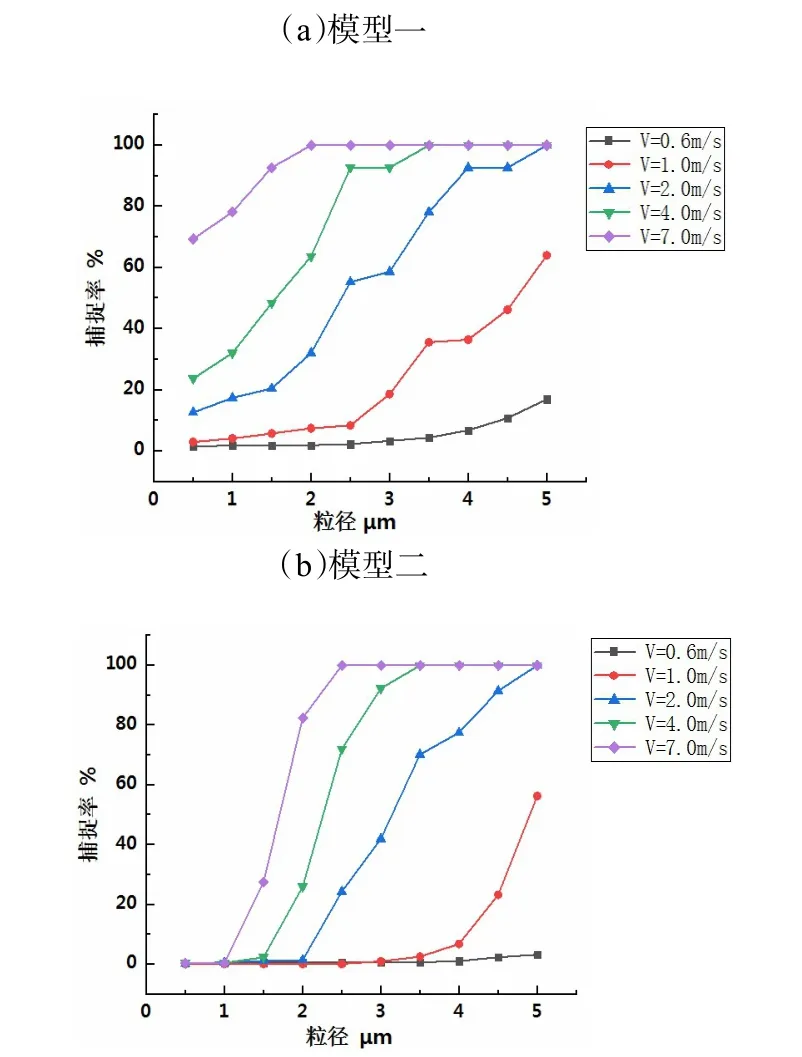
图8 切割头捕捉率曲线

3 结论

1）由入口速度为V=7 m/s 时捕捉面附近速度曲线图分析，模型二切割头比模型一切割头在捕捉面附近速度曲线曲率更大，更符合惯性撞击原理，对于颗粒物从流线分离的效果更强。模型二切割头对于粒径为1.5 μm 和2 μm 的颗粒物捕捉效果有较大的区别，可以有效通过粒径对颗粒物进行选择性捕捉。