基于POD-LSE-FCD 的iBES 异常能耗数据检测方法

马忠娇 张吉礼

大连理工大学建设工程学部

0 引言

2018 年，我国建筑能耗占社会总能耗的36%，其中建造能耗占比为14%，建筑运行能耗占比为22%[1]。目前，我国已在33 个省市建立了国家机关办公建筑和大型公共建筑能耗监测系统，累计对11000 余栋建筑完成了能耗在线监测[2]，形成了建筑能耗海量数据。然而，由于感知层信道的干扰和平台能耗监测技术的不成熟，数据丢失、瞬时异常值和平台固有偏差等问题数据质量问题普遍存在于我国大部分建筑能耗监测平台，严重影响了设备用能特征的深入研究以及后续建筑节能相关措施的实施。因此，提升数据质量至关重要，是数据深入分析的前提。近年来，许多学者及研究机构对建筑能耗监测平台的异常数据检测及修复方法进行了研究[3-9]，为本文的研究提供了很好的借鉴。本文提出了一种将本征正交分解，线性随机估计和分形关联维数相结合的POD-LSE-FCD 方法用于检测异常能耗数据，并将该方法应用于大连某高校节能监测管理平台实际监测数据的异常值检测。

1 POD-LSE-FCD 基本原理

1.1 POD-LSE 基本原理

本征正交分解 POD（Proper Orthogonal Decomposition）是一种源于矢量数据统计分析的方法，利用降维的思想，在损失少量信息的前提下，把多个指标转化为几个综合指标的多元统计方法[10-11]。

若将POD 法应用于能耗数据，则原始能耗数据可表示为矩阵E(x,t)={c(xi,tj)}，其中xi(i=1,2,…,m)为空间坐标，tj(j=1,2,…,n)为时间坐标。理论上，若要精确重构能耗数据矩阵需要一个无限项加和的表达式，而实际上有限数量的POD 模态即可体现数据的变化，故使用下式重构原始数据矩阵：

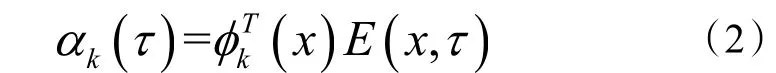
POD 模态的描述方法不是唯一的，直接法需要求解每个变量在整个场上的任意两点相关系数。

式中：COV(E(x,τ))为m×m 维度的协方差矩阵，根据线性代数与拉格朗日函数，COV(E(x,τ))协方差矩阵是一个半正定矩阵；EX{E(x,τ)}为各空间坐标能耗数据在矩阵表示时间段内的期望值，则：

由式(4)可见，λ1，λ2，λ3，…，λm(λ1≥λ2≥λ3≥…≥λm)为协方差矩阵COV(E(x,τ))的m 个特征根，，分别为各特征根对应的标准正交特征向量。此时，已经应用POD 法完成了原始数据矩阵的本征正交分解，并同时给出了原始数据重构后矩阵的均方误差。应用上述方法可用本征正交分解的时间系数来估计原始能耗数据矩阵，再利用基函数重构整个能耗数据矩阵。根据线性随机估计（Linear stochastic estimation，LSE）方法原理，能耗数据的估计矩阵En*(x,τ)表示为：

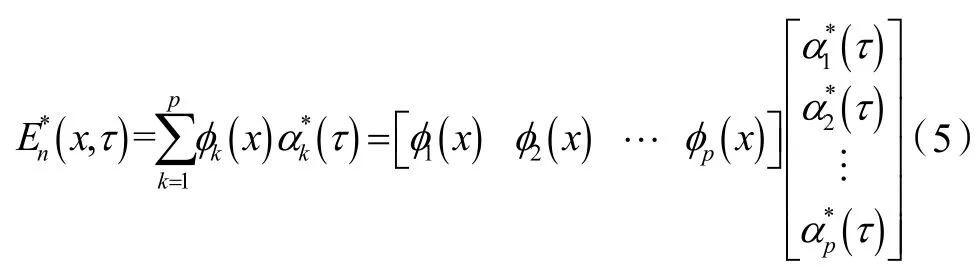
式（5）中估计的时间系数αk*(t)由式（6）计算：

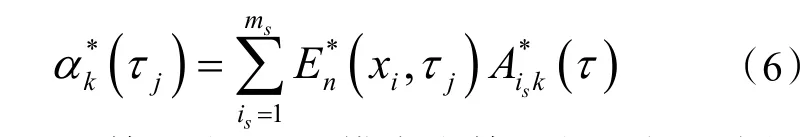
Aisk 是是第k 个POD 模态在第i 个测点的线性随机估计系数矩阵，由下式计算：

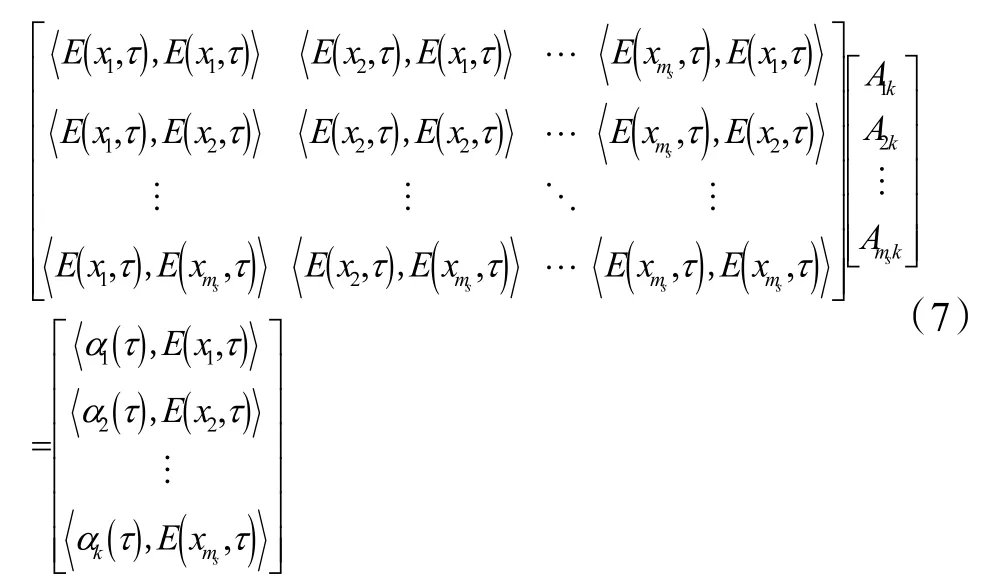
式（7）中E(xi,τ)是原本征正交分解中使用的第i个测点的原测量事件，αk(τ)是根据式（2）计算的第k 个POD 模态的实际时间系数，ms是用于估计整个时间系数的指定空间数据点的数量。

1.2 FCD 基本原理

分形关联维数 FCD（Fractal Correlation Dimension）是在相空间重构过程中求解嵌入维数的一种重要方法。G-P（Grassberger-Procaccia）算法是从一组随机分布的点估计分形标准的分形关联维数的一种主要算法。通过对时间序列的相空间重构，构造的奇怪吸引子在一定程度上反映系统的演化规律。通过分析相空间重构吸引子的结构来评价动力系统的混沌特性，即为G-P 算法的基本思想[12-13]。当应用G-P 方法与POD 耦合时，时间系数αk(tj)应描述如下：

式(8)中n 为表示第k 个POD 模态的一组时间系数序列的长度，时间序列可简化表示如下：

时间序列x(τj)表示在时间τj=τ0+j△τ 处x 值，假设时间序列{x(τj)}的统计量不随时间变化。除非测量值独立同分布，否则连续测量值之间将存在相关性。利用Takens 时延嵌入定理，设m 为嵌入维数且每个相空间有m 个数据点，τs=△τ 为时滞参数，则空间数据的相位可以表示为m 维空间中的一系列点，第j 个时间序列x(τj,m,τs)为：

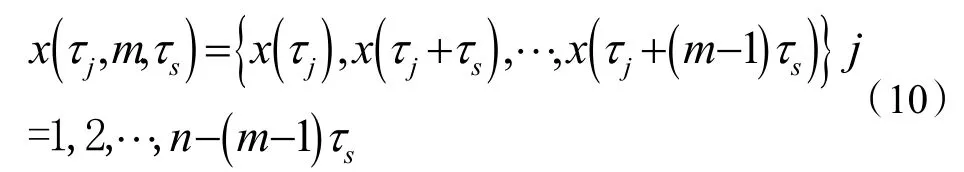
根据上述方法，n 个数据点的时间序列被分成nm组，nm=n-(m-1)τs，nm为分形数组中点的数量或坐标向量的数量，m 维超球半径用欧氏距离表示：

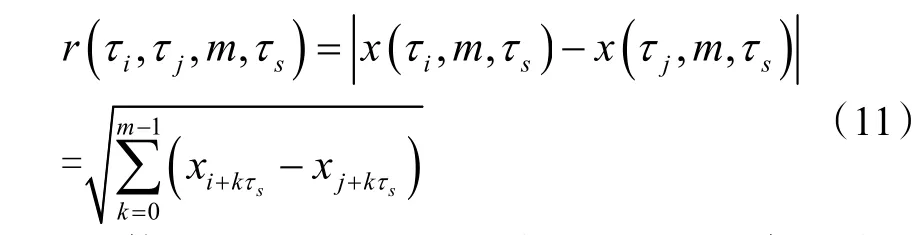
超球体的中心可以定义为半径，且对于每一个i值均可应用球面三角形法从相空间距离中求出一个半径，改变重构的超球体的中心将得到一系列的小球体。如果将r 定义为长度刻度，小球数与总球数之比定义为关联积分函数f(r)：

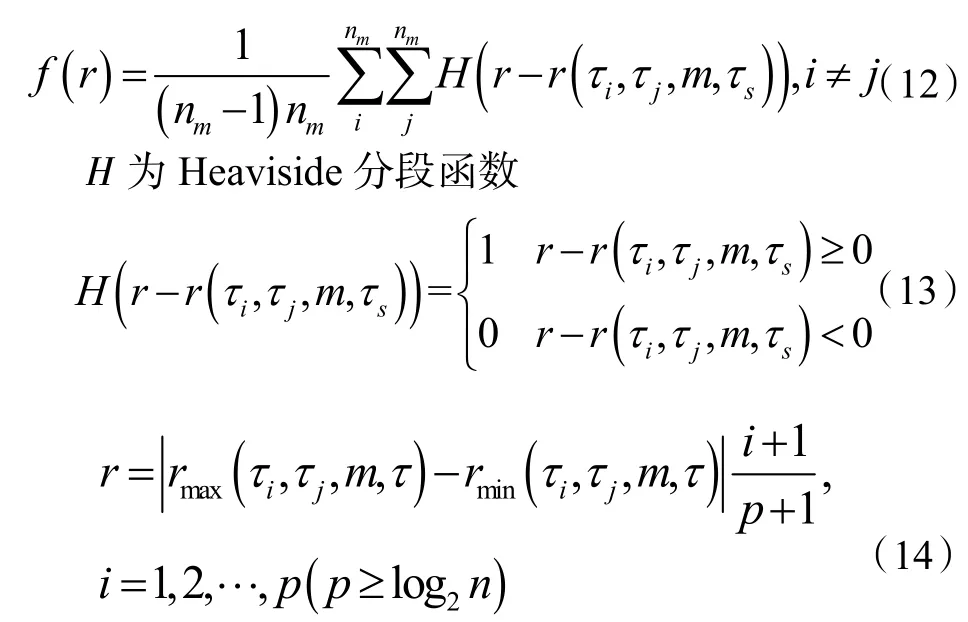
为了避免距离的双重计算导致计算量增大，可将式(12)转换为式(15)：

由于r 足够小且观测值数量nm足够大，分形关联维数重构相空间吸引子为：

综上，C(r)与距离小于r 的分形集的点对数成正比，若所考察的点系是分形集，则DC为双坐标对数图log2C(r)-log2r 在线性区的斜率，斜率DC即为系统的分形维数。

1.3 POD-LSE-FCD 异常数据检测方法基本原理

统计学中基于直接残差的方法通常以实测数据和估计数据之间残差来判断是否有异常值产生。针对能耗数据的非线性特点，本文提出了一种以直接POD和POD-LSE 时间系数的FCD 偏差代替直接残差的方法，即基于POD-LSE-FCD 的异常数据检测方法，该方法的流程图见图1。

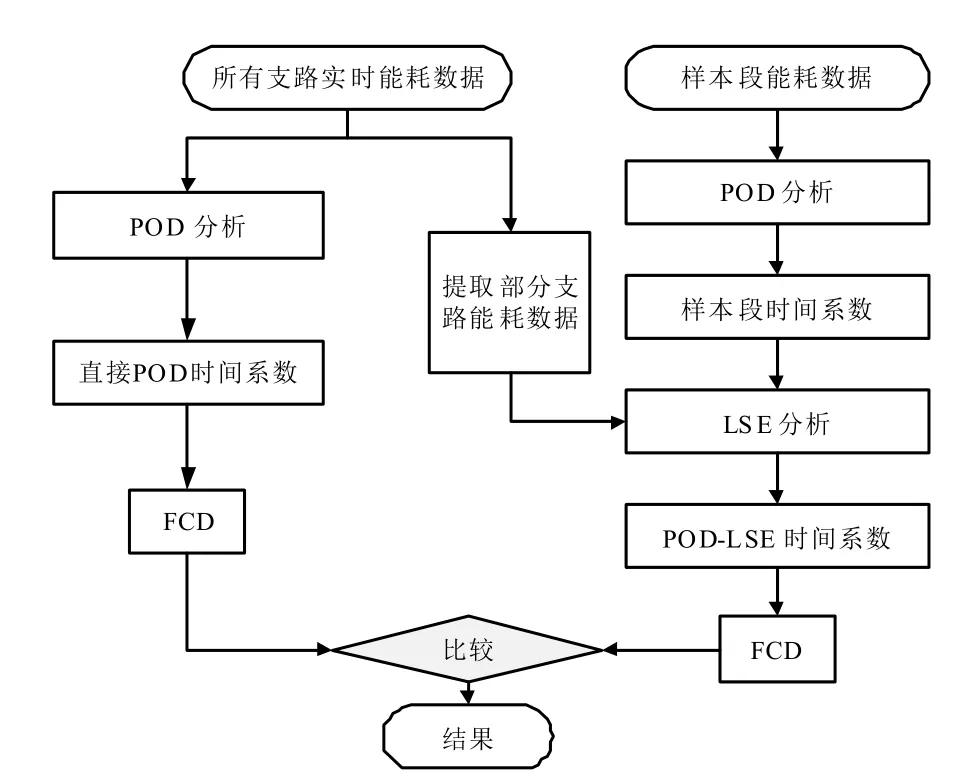
图1 POD-LSE-FCD 法逻辑流程图

研究结果表明，LSE 时间系数能够准确反映能耗监测平台的性能特征。如果直接POD 和POD-LSE 时间系数的FCD 偏差存在较大的差异，则表明直接计算整个域数据的时间系数可能不是正确的系数。因此，可以根据上述原理检测异常的能耗数据。直接POD 和POD-LSE 时间系数的FCD 标准差由式（17）计算：

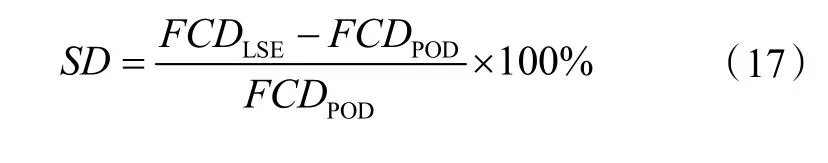
2 POD-LSE-FCD 异常数据检测方法实例分析

本文应用Matlab 自编程序实现了POD-LSE-FCD算法，以大连某高校校园节能监测与管理平台的创新园大楼的照明与插座分项实际监测用电量数据为例，验证了基于POD-LSE-FCD 的异常数据检测方法的有效性。该建筑群分为中央主楼、西侧学生实验楼、东侧创新实验基地，该建筑共有10 个照明与插座用电监测点，应用这10 个支路的数据进行研究，应用2017 年3月1 日-2018 年2 月28 日的逐日数据构成10×365 维能耗数据矩阵。

2.1 POD-LSE 时间系数在全域和选定域一致性的验证法

全域是指所有测点，选定域指的是从所有测点中选取的测点。为了应用本征正交分解降维需验证全域时间系数和选定域时间系数的一致性，本文应用实测能耗数据进行了多次模拟计算与验证，POD-LSE 的详细流程图如图2 所示。

图2 POD-LSE 法逻辑流程图

如图2 所示，第一部分的全域时间系数和选定域时间系数由式（4）的最大特征值计算确定，第二部分的时间系数根据选定域数据和参考时间系数的线性随机估计由式（6）和式（7）确定。参考时间系数是由选定的无数据异常的能耗数据样本段计算确定的（2017 年3 月1 日-2017 年6 月1 日），在计算样本段以外的时间区域内，若存在异常能耗数据，则该异常数据点的POD 时间系数的趋势将显示出明显的误差。

根据式（3），本文计算了不同时间跨度协方差矩阵，结果显示不同时间跨度协方差矩阵的特征值的能量分布高度一致。协方差矩阵第i 个特征值的能量占比表示为Eip，由式（18）计算。图3 为由10×10 协方差矩阵计算出的10 个特征值的能量分布，这表明最大特征值即第1 个特征值捕获了超过81.04%的能量。

图3 特征值能量分布图

根据图3，单一的时间跨度并不代表所有情况，需要验证不同时间跨度异常数据检测结果的区别。本文计算了所有测点和选定测点在相同时间端内的时间系数向量，两个时间系数向量具有相同的维度。图4（a）、图4（b）和图4（c）分别为时间跨度Span=14，Span=28 和Span=56 时直接POD 和POD-LSE 时间系数计算结果对比图。

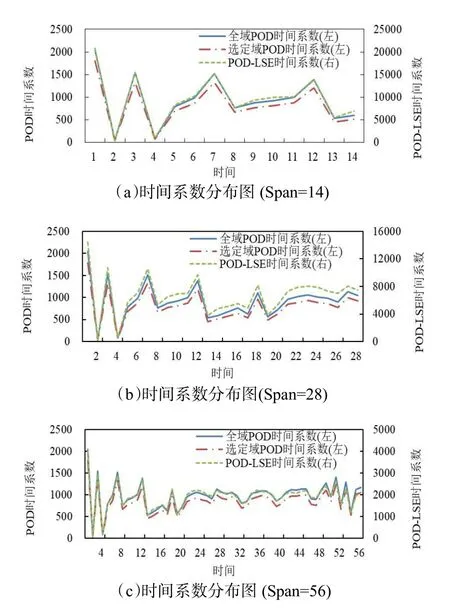
图4 不同时间跨度的时间系数分布图

由图4 可见，随着时间跨度Span 的增加，全域POD 时间系数和选定域POD 时间系数曲线趋于一致，而线性随机估计的POD-LSE 时间系数与全域POD 时间系数和选定域POD 时间系数虽然处于不同的坐标系，其动态变化趋势却保持一致性。

图5 显示了当时间跨度Span=28 时，部分时间的时间系数与能耗数据。由图5 可以看出，尽管时间系数与能耗数据处于不同的坐标轴且量纲不一致，两组数据的动态变化趋势却显示了明显的一致性，异常数据的检测正是基于正常情况下时间系数与能耗数据变化趋势一致这一特性。

图5 时间系数与能耗数据趋势对比图

2.2 POD-LSE-FCD 异常数据检测方法实例的分析结果

通过比较直接POD 和POD-LSE 时间系数的FCD，对实时能耗数据异常值检测方法进行了评价。若将时间跨度设为28，只需要确定1 个参数——步长。若步长设定为Step=7，则每次使用7 个新数据和21个历史数据来计算FCD。同时，在正常情况下选择的参考时间系数的维度与步长相同，应用该算法可检测出异常的能耗数据。直接POD 和POD-LSE 时间系数的FCD 标准差由式（17）计算，图6,图7 和图8 分别为不同步长Step=14，Step=7 和Step=4 的异常数据检测测结果。

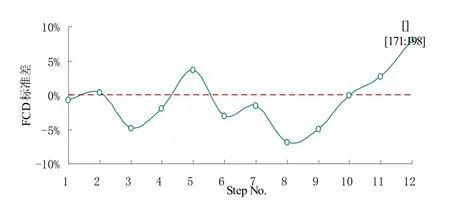
图6 异常数据实时检测结果（Step=14）

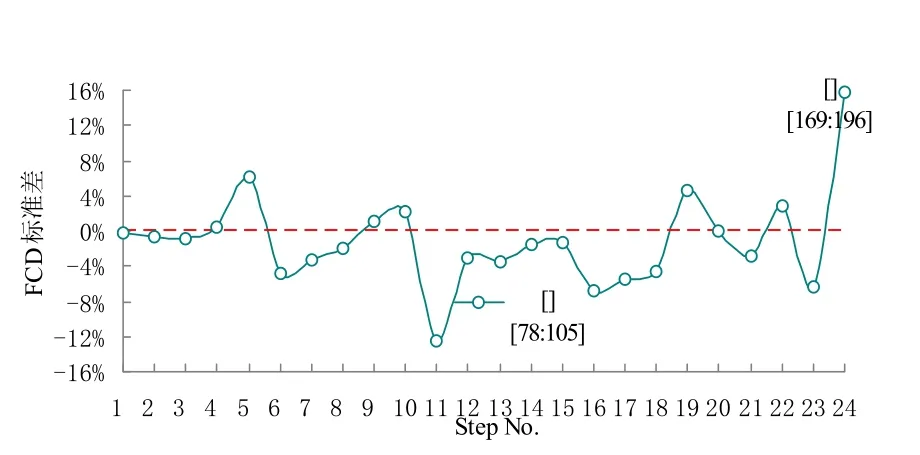
图7 异常数据实时检测结果（Step=7）

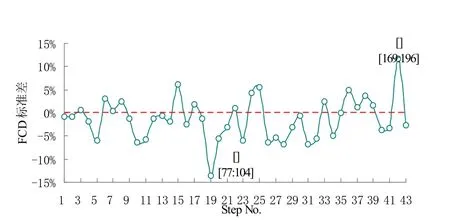
图8 异常数据实时检测结果（Step=4）

如图6 所示，当Step=14 时，检测结果显示在Step No.=12 时，即第12 步时，直接POD 和POD-LSE 时间系数的FCD 标准差SD=8.04%，明显高于其余计算步骤的标准差，该数据点出现的时间为[Start time:End timetime]=[171:198]；如图7 所示，当Step=7 时，检测结果显示在Step No.=11 和Step Noo.=24 时，即第11步和第24 步时，直接POD 和POD-LSE 时间系数的FCD 标准差分别为SD=-12.41%和SD=15.76%，明显高于其余计算步骤的标准差，这两个数据点出现的时间分别为[Start time:End timetime]=[78:105]和[Start time:End timetime]=[169:196]；如图8 所示，当Step=4 时，检测结果显示在Step No.=19 和Step No.=42 时，即第19步和第42 步时，直接POD 和POD-LSE 时间系数的FCD 标准差分别为SD=-13.58%和SD=11.66%，明显高于其余计算步骤的标准差，这两个数据点出现的时间分别为[Start time:End timetime]=[77:104] 和[Start time:End time-time]=[169:196]。

由图6，图7 和图8 还可以看出，当时间跨度Span=28 时，不同步长检测异常值结果略有不同。当Step=14 时，只检测出1 个异常数据点，而当Step=7 和Step=4 时，检测出2 个异常数据点且2 个数据点的位置一致。检测出异常值的步骤，其直接POD 和POD-LSE 时间系数的FCD 标准差SD 均大于8%，明显高于其余计算步骤的标准差。综上，当检测时间跨度Span=28 时，步长Step=7 时最为合适，与Step=14相比较更能准确地检测出异常值的位置，与Step=4 相比减少了计算量。

3 结论

本文提出了POD-LSE-FCD 能耗数据异常值检测方法，该方法将本征正交分解，线性随机估计和分型关联维数相结合。将该方法应用于大连市某高校能耗监测数据，通过比较直接POD 和POD-LSE 时间系数的FCD，对实时能耗数据异常值检测方法进行了评价。分别模拟计算了当时间跨度Span=28 时，不同步长Step=14，Step=7 和Step=4 的异常数据检测测结果，得出以下结论：

1）当时间跨度Span=28 时，不同步长检测异常值结果略有不同：当Step=14 时，只检测出1 个异常数据点。当Step=7 和Step=4 时，检测出2 个异常数据点，且两个数据点的位置一致。

2）检测出异常值的步骤，直接POD 和POD-LSE时间系数的FCD 标准差均大于8%，明显高于其余计算步骤的标准差。

3）当检测时间跨度Span=28 时，步长Step=7 时最为合适，与Step=14 相比较更能准确地检测出异常值的位置，与Step=4 相比减少了计算量。

综上，POD-LSE-FCD 法可以准确并快速的检测出能耗异常数据，适宜应用于iBES 建筑能耗监测平台异常数据诊断。