北方农村地区分布式能源系统综合评价
任志刚 陈昕 邓勤犁 周军莉
武汉理工大学土木工程与建筑学院
0 引言
随着建筑面积的扩大和生活水平的提高,建筑能耗在不断增加[1]。2018 年,我国建筑能耗在社会总能耗中占比达到36%,其中农村居住建筑能耗占全国建筑总能耗的22%[2]。分布式能源系统因其对能源的“梯级利用”准则,使得其具备较高的能源利用效率[3],能有效避免因能效低下产生的能源过度消耗。将分布式能源系统应用于我国农村地区可以有效改善农村居住建筑目前“低能效、高能耗”的状况。
本文建立了考虑能源、经济、环境三方面效益的评价指标体系,提出了基于组合赋权法和优劣解距离法(Technique for Order Preference by Similarity to an Ideal Solution,TOPSIS)的分布式能源系统评价方法。以山东省济南市刚家村为例,构建了三套适用于该村的能源系统方案,并利用上述评价指标和评价方法对三种方案进行综合评价。
1 指标体系
科学的指标体系不仅是多指标综合评价的前提,也是科学、公正结论的保证[4]。本文构建如表1 所示的评价指标体系,其中能源消耗量是指系统消耗燃气热量加上使用电量转换为燃煤消耗的能量;能源利用率是系统输出的能量与能源消耗的比值。初投资指系统设备总投资费用;运行维护费用包括系统维护和年燃料费用之合。
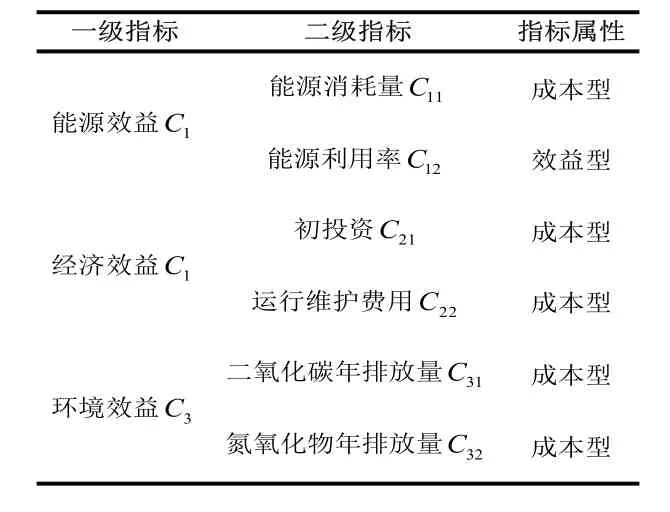
表1 分布式能源系统评价指标体系
2 评价方法
1)组合赋权法
由于实际中不同指标在系统评价过程中的影响程度不同,因此须对各项指标分配权重以反映其各自的重要程度。权重是否合理直接关系到综合评价结果的准确性[5]。权重的确定方法分主观法和客观法两大类[6]。本文采用一种结合主观权重和客观权重的组合赋权方法来确定不同层次的指标权重以区分其各自影响程度的差异性。
层次分析法作为一种定性与定量分析系方法相结合的综合主观评价方法,在多个领域得到广泛应用,其主要的计算分为三步[7]:建立比较矩阵;求比较矩阵的最大特征向量,并进行一致性检验;归一化处理得到权重。熵权法是一种客观赋权方法,它是利用各指标的熵值所提供的信息量大小来决定指标权重的方法,其计算过程如下[8]:明确评价问题,构建决策矩阵;对决策矩阵中各指标值进行无量纲化处理;计算各指标的熵值及差异系数;计算指标权重。
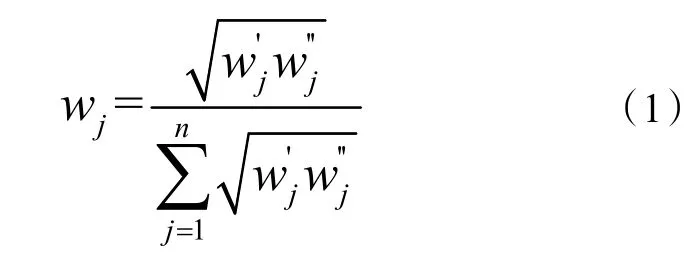
2)TOPSIS 评价法
TOPSIS 称为“优劣解距离法”,是一种多目标决策方法[10]。该方法是根据评价对象与理想方案的相对贴近程度,对众多评价对象整体排序从而确定方案之间的相对优劣,具体计算步骤如下[11]:对原始数据归一化处理,并利用组合权重对处理后的各项数据进行赋权,构成归一化后赋权的决策矩阵;确定理想解和负理想解;采用加权的欧几里得范数,度量实际解到理想解的欧几里得距离;计算每个实际解距离理想解的相对贴进度,按由小到大的顺序排列方案的优劣次序。该值越大,说明方案距离理想解越近,负理想解越远,说明该方案具有更好的综合效益。
3 实例分析
3.1 研究对象
本文以山东济南市商河县刚家村为研究对象,其位于济南市北部,属于寒冷地区。刚家村共有居民353户,每户3 至4 人,且各农户位置分布集中,因此适合分布式能源系统的应用。根据实地调研情况,本文选取该村一栋典型住宅,其建筑平面图如图1 所示。典型住宅外墙为“三七”墙,内墙为“二四”墙;屋顶为坡屋顶;窗为木框单层玻璃,窗高均为1.5 m;冬季采暖区域为两个卧室以及客厅。
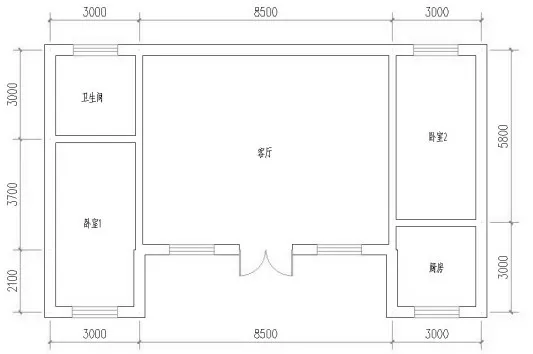
图1 刚家村典型住宅建筑平面图
利用EnergyPlus 软件对典型住宅供暖热负荷进行模拟,根据总农户数量和模拟结果推算刚家村的总体供暖热负荷。依照《建筑给水排水设计规范》(GB50015-2019)[12]中的规定,生活热水为每人每天40 L,冬季、夏季和过渡季的生活热水加热温差分别取35、25、30。全村每月用电量数据来源于当地电业局,如表2 所示。最后利用逐时分摊系数,得到全年逐时热水负荷与电负荷。各季节典型日逐时负荷见图2。
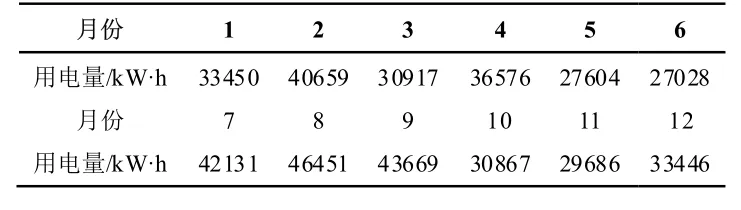
表2 刚家村月用电量

图2 刚家村各季节典型日负荷
电负荷与热水负荷的波动与人员作息相关,主要集中于晚间六点至十点。在冬季,农村居住建筑对供热的热力需求远大于对电力需求,主要原因有两点:一是,与城市居住建筑相比,农村居住建筑由于家电数量与居民用能习惯等方面的影响,建筑的电力需求尚处于较低水平,户均月用电量仅为100 kW·h。二是由于农村住宅围护结构保温措施不完善,导致建筑供暖热负荷较高。
3.2 能源系统方案
根据刚家村的规模和用能需求,本文构建了三种可用于该村的能源系统方案,即:传统分布式能源系统,天然气分布式能源系统和沼气分布式能源系统。系统承担用户的电负荷、供暖热负荷与热水负荷。
如图3 所示,传统分供式系统从电网购电满足用户电负荷E,利用燃气锅炉和燃气热水器承担用户供暖热负荷Qh和热水负荷Qc。通过建筑负荷和设备参数计算分供式能源系统的项指标数据值。

图3 传统分供式能源系统
分布式能源系统的运行模式主要分为两种,即“以电定热”和“以热定电”。考虑到我国很多农村地区的电力“上网”政策尚不完善,所构建的分布式能源系统以“以电定热”的模式运行。燃气供给内燃机发电机进行发电,产生的电能用于建筑电气照明设备等的供应,即系统优先满足用户的电力需求。发电后的系统余热通过热回收系统进行回收,以满足用户的热力需求。当热回收系统所回收的热量无法满足用户的热力需求时,则通过燃气锅炉进行补充供热。
利用TRNSYS 软件对分布式能源系统进行模型搭建,分别模拟天然气分布式能源系统和沼气分布式能源系统。将用户负荷和设备参数代入模型进行模拟,以此分别计算天然气和沼气分布式能源系统的指标数据。
3.3 结果与分析
计算得到三种能源系统方案的各项指标具体数值如表3 所示。可以看到,分布式能源系统在能源效益和经济效益方面显著优于传统分供式能源系统。分布式能源系统具有较高的能源利用率与较少的能能源消耗量,与之伴随的是燃料费用降低和更好的环境效益。传统分供式能源系统的初投资为124.8 万元,低于另外两种分布式能源系统,这是由于分布能源系统需安装发电设备,发电设备。沼气分布式能源系统与天然气分布式能源系统主要的区别体现在经济效益方面。沼气作为燃料,须对沼气进行净化、压缩等预处理,预处理设备所需的费用导致沼气分布式能源系统的初投资较高,但沼气价格低于天然气价格,使其在运行维护费用方面占有优势。
采用层次分析法确定主观权重,通过一致性检验。通过熵权法利用指标数据计算得到客观权重。最后由式(1)得到组合权重。从图4 中可以看出,主观和客观权重之间具有较大差异,主观权重中经济效益占据较大比重,而客观权重中则是能源效益。主观和客观权重之间的差异表明,使用单一方法进行赋权会导致结果不准确。综合主、客观的组合赋权法将兼顾对指标的主观偏好,同时又减小主观随意性,能使对指标的赋权达到主客观相统一。
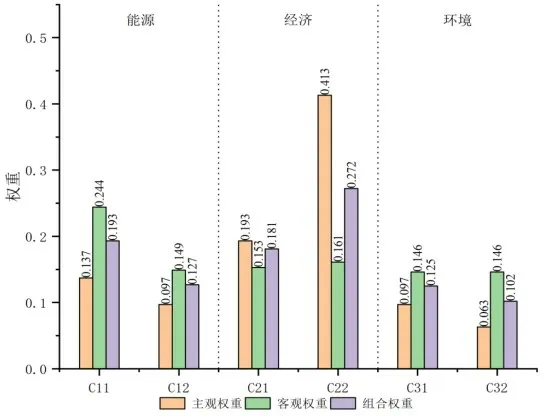
图4 各评价指标主观权重、客观权重以及组合权重
利用TOPSIS 方法对各方案进行综合评价。各方案距理想解的相对贴进度见表4 所示。各方案由优到劣的排序依次为:天然气分布式能源系统、沼气分布式能源系统、传统分供式能源系统。传统分供式能源系统的相对贴近度远小于天然气和沼气分布式能源系统,说明在我国北方农村地区,分布式能源系统将比传统分供式能源系统具有更好的综合效益。分布式能源系统在初投资方面具有劣势,但其在其他指标方面的优势足以弥补这一不足。天然气分布式能源系统与沼气分布式能源系统的相对贴近度接近。考虑到农村地区有大量的生物质资源可用作制备沼气的原料,沼气分布式能源系统为农村大量废弃生物质资源提供了有效的利用途径,也为当地农民增加了创收机会。因此在一些情况下,沼气分布式能源系统可作为农村村级分布式能源系统的优先选择。

表4 方案相对贴近度值
4 结论
本文建立了一套针对我国北方农村地区村级分布式能源系统的综合评价方法,采用主观赋权-层次分析法和客观赋权-熵权法相结合的组合赋权法确定指标权重,运用TOPSIS 评价方法,计算各方案的相对贴近度,以此对方案进行优劣排序。最后以山东省商河县刚家村为例进行实例分析。论文得到以下结论:
1)主观赋权法与客观赋权法的结果具有较大差异,综合主、客观的组合权重将兼顾对指标的偏好,同时又减小主观随意性,使对指标的赋权达到主客观相统一。
2)在我国北方农村地区,分布式能源系统将比传统分供式能源系统具有更好的综合效益,天然气分布式能源系统略优于沼气分布式能源系统。若考虑对当地生物质资源的有效利用,沼气分布式能源系统是我国北方农村地区能源系统的优先选择。

