教室内不同送风方式气流组织有效性对比

顾婷婷 邓利艳 郭琦 赵昊鹏 齐贺闯* 叶筱 亢燕铭

1 上海工程技术大学机械与汽车工程学院

2 东华大学环境科学与工程学院

0 引言

目前教室内普遍采用的空调送风方式为上送上回式的混合通风（Mixing Ventilation，MV），研究表明，该送风方式在冬季供暖时存在能耗高且局部热舒适度差等问题[1-4]。碰撞射流通风（Impinging Jet Ventilation，IJV）作为一种新型通风策略，近年来引起了国内外众多研究者的关注[4-7]。其通风原理为：送风气流以较高的动量从房间下部垂直射出，与地面发生碰撞后，在惯性力的作用下沿着地板水平扩散，并在地板上方形成一层很薄的“空气湖”，回风则从位于房间上部的回风口排出[7]。

为评价碰撞射流在用于教室热风供暖的可行性，本文针对冬季供暖工况，对比研究不同送风温差条件下碰撞射流通风与混合通风在教室热风供暖时的室内热环境分布特征，以期为冬季教室内热环境改善和空调送风系统的合理化设计提供参考。

1 计算模型与方法

1.1 物理模型和边界条件

以一长×宽×高为7.2 m×11 m×3.5 m 的教室作为物理模型进行研究。为尽可能接近实际，教室设有56个学生（均为坐姿状态）和27 盏灯，如图1 所示。人体和灯光散热量分别设为38 W/人和15 W/盏。

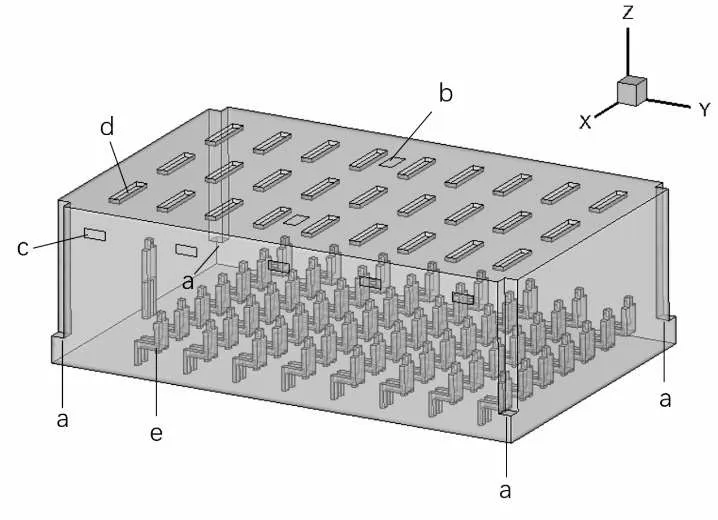
图1 模拟教室平面布置图

分别采用碰撞射流通风和上送上回式的混合通风两种送风方式对教室进行热风供暖。IJV 的四个送风口位于教室的四个墙角处，送风口尺寸为0.3 m×0.3 m，送风口距地面的高度为0.6 m。对于MV，五个送风口（尺寸均为0.5 m×0.16 m）均布置在侧墙上方，送风口中心距离地面的高度为3.0 m。两种送风方式的排风口（尺寸为0.6 m×0.3 m）均设在天花板上。两种送风方式的风口布置如图1 所示。

忽略冷风渗透造成的热损失，认为冬季房间热负荷主要来自四周侧墙和屋顶的热损失。墙面边界条件按恒定热流密度边界设定，侧墙热流密度均设为-24 W/m2，屋顶热流密度强度设置不同，详见表1。所有固体表面均设为无渗透和无滑移条件。送风口边界类型设为velocity-inlet，并假定流速均匀，排风口边界定义为outflow。

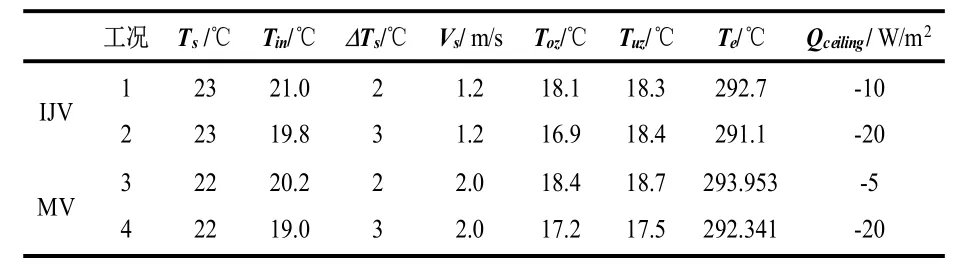
表1 计算工况的基本参数

1.2 研究方法及验证

认为室内空气设为连续、不可压缩流体，流体的基本属性不随时间发生变化，空气密度采用Boussinesq假设[8-9]。RNG k-ε 湍流模型模拟室内空气流动具有较好的可靠性且求解简单省时[10-11]，所以采用该模拟计算。模型的离散化中除压力项采用标准格式离散外，其他项均采用二阶迎风格式。采用SIMPLE 算法处理压力项和速度项的耦合。计算空间采用非结构化四面体网格进行划分，并且对室内热源表面、送风口、回风口等区域网格进行加密处理，最小网格尺寸0.05 m，增长因子1.15，最终网格总数分别为310 万（IJV）和298万（MV）。

文献[12]对置换通风室内温度和速度分布进行了实测，本文采用与之相同的物理模型、边界条件及室内热源条件进行数值模拟：房间尺寸长×宽×高为3.65 m×5.16 m×2.43 m，换气次数4 次/h，送风温度17 ℃，室内热源为2 个人（表面温度28～30 ℃）、2 台电脑（散热量为173 W 和108 W）、6 盏灯（散热量为34 W）、墙壁表面温度为23.3～26.0 ℃。

图2 给出了房间中心位置处气流速度和温度沿高度分布的结果对比。从该图可知本文获得的模拟结果与文献[12]的结果吻合较好，表明本文中使用的数值计算方法具有一定可靠性。

图2 数值模拟结果与实验结果对比

1.3 研究工况

分别对送风温差ΔTs为2 ℃和3 ℃的情况进行数值模拟。模拟时，送风参数，室内热源及四周墙面的热流密度恒定，通过改变屋顶热流密度强度实现不同送风温差条件。送风参数如表1 所示。

2 模拟结果与分析

2.1 不同送风方式下流场和温度场分布特征

图3 给出了送风温差ΔTs=2 ℃时，IJV 和MV 两种送风方式所对应的过房间中心剖面(y=5.5 m 平面)上的温度流线分布。

图3 y=5.5 m 平面上的流场和温度场分布

由图3（a）可知，IJV 在房间内的流场关于房间中心剖面y=5.5 m 平面对称分布，且整体空间温度分布较为均匀。这是因为，IJV 的送风气流以较高动量从送风口向下射出并撞击地面，随后沿地面水平扩散一定距离后在热浮力的作用下上浮，送风气流自下而上地与室内空气混合，最终形成了覆盖房间大部分空间的大涡流，这使得房间内的气流在惯性力的主导作用下充分混合，从而使室内温度均匀分布。

由图3（b）可以看到，在MV 中，送风气流从风口水平射出后，在热浮力和惯性力的共同作用下，气流运动轨迹由水平运动转变为斜向下运动。在遇到室内热源后，气流动量大幅衰减，此时热浮力起主要作用，气流运动轨迹改为向上运动，最终在房间中心处形成一个较大的涡流区，且该区域内温度明显低于其他区域。另外，由图3（b）还可知，与送风口同侧的近地面区域温度明显低于同高度其他区域，表明送风热气流不能与室内空气充分混合，这与供冷情况有显著差异[13-14]。

气流形态和温度分布特征的差异势必会带来不同的空调效果，为对比IJV 和MV 两者的送风有效性，下文将利用不同评价指标进行对比分析。

2.2 不同温差下气流组织有效性的评价

2.2.1 不均匀系数

采用温度不均匀系数和速度不均匀系数进行评价，其定义式分别为：

式中：Kt和Kv分别为温度不均匀系数和速度不均匀系数，Kt和Kv的数值越小，则气流分布的均匀性越好。n为测点数，ti为测点温度，ui为测点速度，t 为测点平均温度，u 为测点平均速度。

图4（a）和（b）分别给出了IJV 和MV 两种送风方式下的室内温度和速度不均匀系数。由图4 可以看出，IJV 房间内的温度和速度均匀性较好，能保证较好的舒适度。

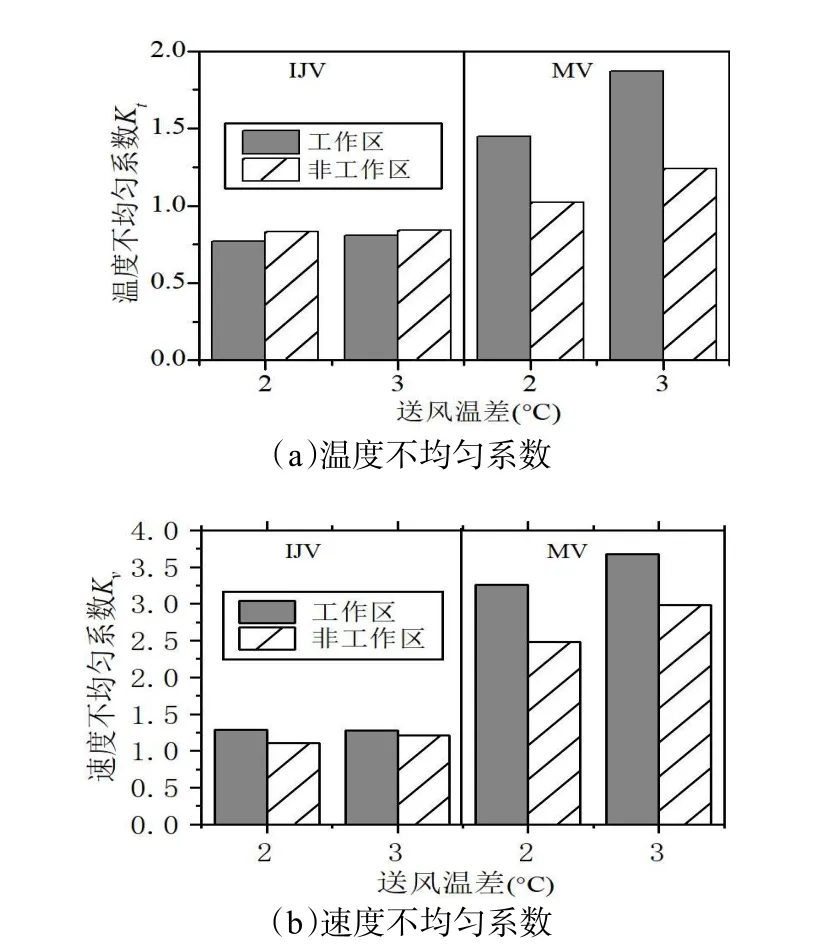
图4 不同送风温差下IJV 和MV 房间温度和速度不均匀系数对比

图4 的结果表明，对于IJV，温度不均匀系数和速度不均匀系数基本不随送风温差的变化而改变，而对于MV，Kt和Kv均随送风温差的增大而增大。这是因为，在用于冬季热风供暖时，IJV 将具有较大动量的气流直接送至房间下部，在惯性力和浮力的综合作用下与室内空气自下而上地混合，而MV 的送风热气流从房间上部送入室内，由于热浮力的作用，热气流很难到达房间下部人员活动区，且送风温差越大，送风气流受到的浮力作用越显著，送风气流与下部空间空气的混合越不充分（见图3）。

此外，由图4 还可知，IJV 房间内工作区的温度和速度不均匀系数基本与非工作区保持一致，而MV 房间内工作区的温度和速度不均匀系数均远大于非工作区的，这是因为，在热浮力作用下，MV 的送风气流与工作区气流难以充分混合，导致较大的工作区温度和速度不均匀系数。

2.2.2 吹风感

图5 给出了送风温差ΔTs=2 ℃时，IJV 和MV 房间内近地面区域z=0.1 m 平面（对应于人体脚踝高度）上的速度分布。由图5 可以发现，由于IJV 的送风气流直接送至房间下部，导致其室内z=0.1 m 平面上的气流速度明显大于MV，特别是对于送风口附近，气流速度之间的区别最为明显。较大的气流速度极易引发吹风感，为此，分别对IJV 和MV 两种送风方式所对应的脚踝高度平面（z=0.1 m 平面）上的平均吹风感进行对比研究。

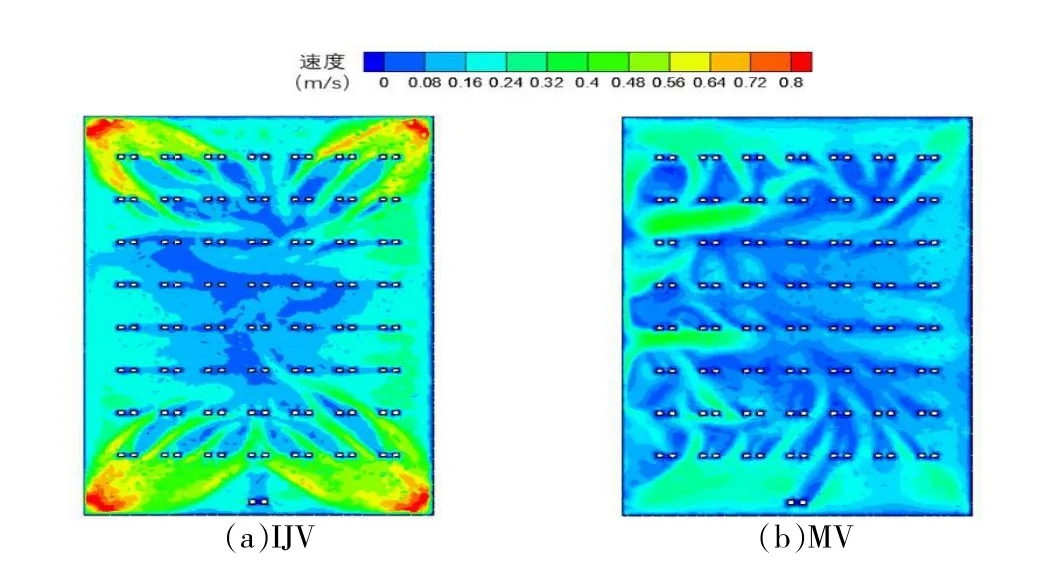
图5 IJV 和MV 房间内近地面区域z=0.1 m 平面上的速度分布

Fanger 等人将湍流强度表征为气流湍动变量，总结出因吹风感引起的不满意率（PD），ASHRAE 标准规定由于风感引起的吹风感不满意率不应超20%。

式中：Ti为对应测点温度，K；ui为对应测点风速，m/s；Ii为对应测点湍流强度，%。其中：当u＜0.05 m/s 时，u 取0.05 m/s；当PD＞100%时，PD 为100%。

图6 给出了不同送风温差下，IJV 和MV 供暖房间内z=0.1 m 平面上的吹风感对比。送风温差为2 ℃和3 ℃时，IJV 的PD 值分别为18.5%和18.3%，表明IJV 的PD 值不随送风温差的改变而改变。MV 的PD值在送风温差为2 ℃时为15.3%，在送风温差为3 ℃时为13.1%，表明MV 的PD 值随着送风温差的减小而减小。对于不同送风温差，尽管IJV 的PD 值高于MV 的，但仍处于ASHRAE 的标准限值20%。

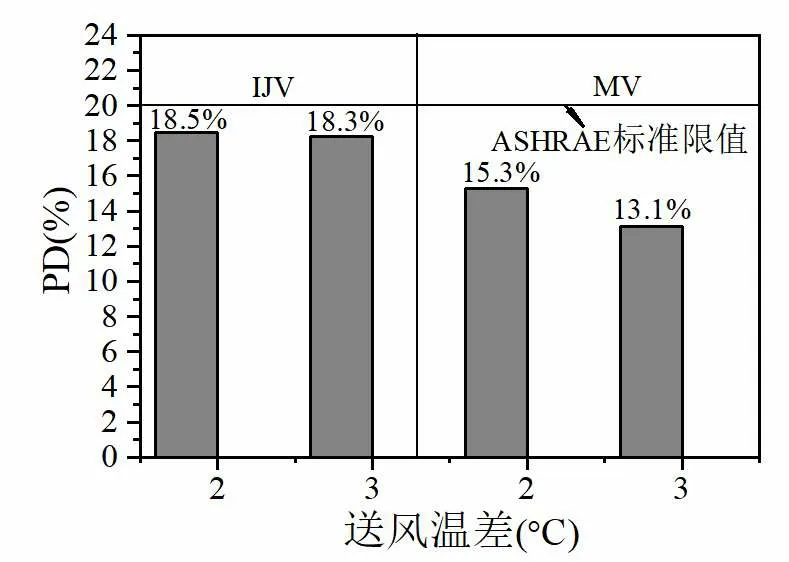
图6 吹风感对比

2.2.3 能量利用系数

利用能量利用系数评价气流分布的能量利用有效性：

式中：Tuz为非工作区平均温度，Toz为工作区平均温度，Ts为送风温度。

由图7 可知，对于不同送风温差，IJV 的能量利用系数均接近于1，而MV 的能量利用系数远小于1，对于本文所研究工况，MV 的EUC 最大不超过0.6。这意味着，与MV 相比，IJV 具有显著的节能效果。此外，图7 还表明，MV 的能量利用系数随送风温差的增大而减小，这是因为，送风温差越大，送风气流受到的热浮力作用越明显，进入房间下部的热气流越少。

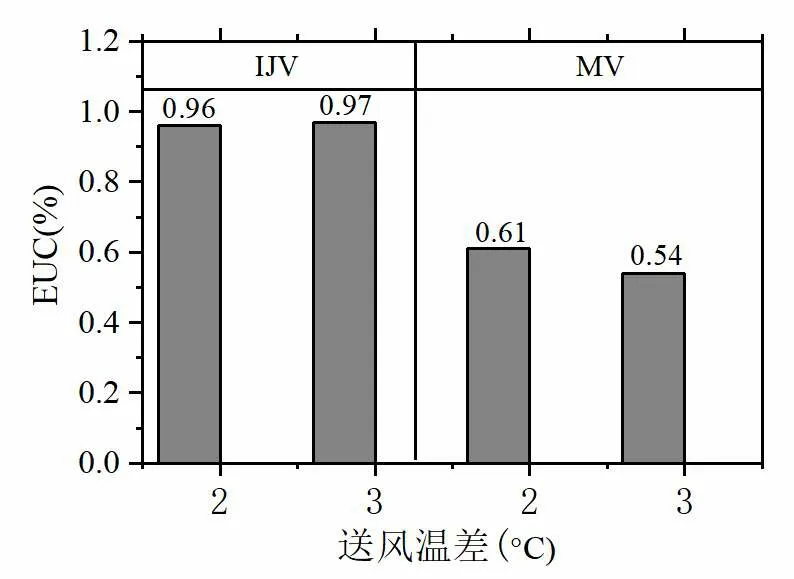
图7 能量利用系数对比

3 结论

本文数值模拟了教室在采用IJV 及MV 进行热风供暖时的流场，利用不同评价指标对两种气流组织进行了对比研究，结论为：

1）IJV 供暖时，送风热气流能够与房间下部空间的空气充分混合，而MV 的送风热气流因热浮力作用只有少部分进入下部空间，导致人员活动空间温度和速度的分布极不均匀。

2）尽管IJV 房间内近地面区域的气流速度高于MV 的，但PD 分析结果表明，不同送风温差下，IJV 房间内人体脚踝高度平面上的PD 平均值仍处于ASHRAE 标准规定范围内，不会给人体造成热不舒适吹风感。

3）对于不同送风温差，IJV 的能量利用率基本保持在1.0 左右，而MV 的能量利用率明显小于1，且送风温差越大，能量利用率越小，意味着在供暖时IJV 比MV 具有较好的节能效果。