航空发动机双转子系统叶片-机匣碰摩故障模拟

靳玉林，刘治汶，陈予恕

1. 电子科技大学 自动化工程学院，成都 611731

2. 西南交通大学 机械工程学院，成都 610031

3. 哈尔滨工业大学 航天学院，哈尔滨 150001

转子-轴承系统是航空发动机的“核心结构”，尤其是先进燃气涡轮发动机普遍采用双转子-滚动轴承支承结构，具有结构复杂、多支点弹性支承、零部件众多、装配工艺复杂、运行环境恶劣等特点。因此航空发动机双转子系统易出现不平衡、不对中等故障[1]。此外先进燃气涡轮发动机普遍采用小间隙设计[2-8]，并由于低压转子柔性结构设计、转子/静子非均匀热膨胀、强离心载荷以及复杂的整机动力学行为等因素的存在，导致双转子系统在很大程度上可能发生叶片-机匣碰摩故障。叶片-机匣碰摩容易引起叶片损伤，甚至导致叶片断裂、发动机着火等事故，严重影响发动机的运行稳定性及安全性[2]。

转-静碰摩是指高速旋转的转动部件与静子机匣/密封发生碰撞、接触和摩擦等物理现象[7]。国内外对转-静碰摩故障已有大量研究，获得了丰硕成果[2-16]。Ahmad[2]综述了转子-机匣接触碰摩的研究现状，总结了刚度、阻尼、库仑摩擦、转速、支承结构不对称、热效应等物理参数对转-静碰摩的影响。Georges等[3]从碰摩物理模型、热效应、数值及实验研究等方面对涡轮机械转-静接触问题进行了文献综述。李勇等[4]利用航空发动机模型转子测试了转-静碰摩的叶片振动载荷和振动特性。马辉等[5]对旋转机械转-静碰摩故障的实验研究进行了详细综述，总结了单点、局部及全周碰摩的故障特征；此外他们也对有/无涂层的转子叶片-机匣碰摩力学模型，以及相应的碰摩动力学特征进行了总结[6]。Chen[8]对航空发动机单转子系统的叶片-机匣碰摩进行了动力学建模，给出了碰摩故障的振动响应特征，并进行了实验验证。Wang等[9]研究了航空发动机风扇叶片断裂诱导的碰摩故障特性，并进行了实验验证。陈雪峰等[10]针对航空发动机碰摩故障响应信号微弱、频率快变的特点，提出了匹配同步压缩变换方法，给出了碰摩故障诊断的新技术。

然而过去关于转-静碰摩问题的研究以单转子系统为主，关于航空发动机双转子系统的转-静碰摩故障的研究在近十年来得到了较多关注。杨洋[7]建立了定点碰摩的航空发动机双转子系统的动力学模型，数值分析了双转子系统在不平衡激励作用下的定点碰摩故障振动响应，并通过实验验证了碰摩力模型的有效性。王四季等[11]通过实验研究了对转双转子系统局部碰摩的振动特性。陈松霆和吴志强[12]建立了反向双转子碰摩系统的动力学模型，分析了系统参数对振动响应的影响。罗桂火等[13]利用有限元软件及自由界面模态综合法，建立了含碰摩故障的高维双转子系统的动力学模型，分析了反向旋转双转子系统的碰摩故障动力学特性。Sun等[14]利用ANSYS 软件建立了某型航空发动机双转子系统的实体单元模型，采用模态综合法获得了高精度降阶模型，并利用谐波平衡-时频转换技术及弧长沿拓法分析了双转子系统主共振区间的非线性碰摩特性。Yu等[15]研究了航空发动机双转子系统的风扇叶片断裂甩出诱导的碰摩振动响应特性，定量分析了不同支承刚度下，风扇突加大不平衡离心载荷对不同支承轴承的影响，并分析了大不平衡载荷下出现的碰摩动力学行为。孙涛等[16]利用有限元法建立了反向旋转双转子系统的碰摩动力学模型，采用Wilson-θ法进行数值求解，分析了碰摩故障的非线性响应特性。

以上关于航空发动机双转子系统的转-静碰摩问题的研究主要基于简化的双转子动力学模型，未综合考虑发动机支承轴承非线性以及复杂装配结构的不对中、不平衡等因素；此外，碰摩力模型为经典的边界约束模型[11-16]，虽然近年来有学者提出了更完善的叶片-机匣碰摩模型[17-19]，但相关模型还未应用于航空发动机双转子系统叶片-机匣碰摩问题的研究。

针对航空发动机双转子系统，考虑支承轴承非线性、高低压转子联轴器不对中、高低压转子轮盘不平衡以及低压压气机轮盘叶片-机匣碰摩力学模型，利用有限元法建立整机双转子系统的非线性动力学模型；利用模态综合法缩减系统自由度，并数值求解降阶模型的非线性振动响应。同时，通过实验测试不同转速及不同转速比的碰摩振动响应信号，确定双转子系统叶片-机匣碰摩的故障特征。该研究结果及分析方法对于航空发动机双转子系统碰摩故障诊断及叶尖间隙设计具有一定的参考价值。

1 实验台双转子系统动力学建模

1.1 双转子系统简化力学模型

基于航空发动机实验台的双转子系统简化有限元模型如图1所示，设高低压转子同轴，高低压转子通过中介轴承(轴承4)套装在一起，并通过高低压控制电机驱动。在惯性坐标系O-xyz下，仅考虑系统横向振动，假设高低压转轴几何匀称，材料均匀，转轴为空心轴，可利用有限元方法将转轴离散为26个梁单元，共28个节点(N1～N28)。根据轮盘、轴承、联轴器位置将高低压转轴划分为7个轴段，低压转子划分为4个轴段，对应的单元数分别为2、2、10、2；高压转子划分为3个轴段，对应的单元数分别为2、4、4。实验台双转子系统的结构参数如表1所示。各个支承轴承的结构参数如表2所示。

各支承轴承的几何中心以及各轮盘的几何中心位于相应节点位置(图1)，考虑各支承座径向面内的弹性变形、各支承轴承非线性、各轮盘不平衡、高低压联轴器不对中、以及低压压气机叶片-机匣碰摩，利用有限元法可建立该系统的动力学模型。

1.2 双转子系统有限元模型

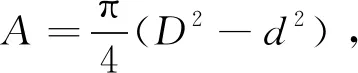
图1 航空发动机实验台双转子系统有限元模型

表1 双转子系统结构参数

表2 支承轴承结构参数

图2 双转子系统有限元模型

利用拉格朗日方程可获得转子第i个单元的动力学方程[20]：

(1)

同样，利用拉格朗日方程可获得转子第i个刚性轮盘的动力学方程[8, 20]：

(2)

式中：Md为刚性盘质量惯量矩阵；Gd为刚性盘陀螺矩阵；Fd为刚性盘受的外力向量。

考虑系统不平衡、不对中、支承轴承非线性、叶片-机匣碰摩，可获得实验台双转子系统的叶片-机匣碰摩耦合动力学方程：

(3)

式中：q为系统坐标向量；M、C、K分别为系统质量、阻尼以及刚度矩阵；GL、GH为低、高压转子陀螺矩阵。F(q,t)=Fb+Fr+Fc+Fg+Fu，Fb为轴承力；Fr为叶片-机匣碰摩力；Fc为联轴器不对中力；Fu为不平衡激励力；Fg为重力；ωL、ωH分别为低、高压转子转速。

假设实验台双转子系统的阻尼为比例阻尼，因此系统阻尼矩阵C可表示为α0M+α1K，α0、α1为比例阻尼系数，可通过模态实验获得。

1.3 联轴器不对中模型

航空发动机转子结构复杂，在装配或运行过程中不可避免存在不对中。联轴器不对中模型包含：平行不对中、角度不对中、组合不对中。由于实验台的联轴器为柔绳连接的一对法兰盘，因此其不对中模型可近似认为是平行不对中，如图3所示。作用在高低压转子的联轴器不对中力可表示为[21]

(4)

式中：Fcx、Fcy分别为x和y方向上的联轴器不对中力；mc为联轴器质量；Δl为不对中量。

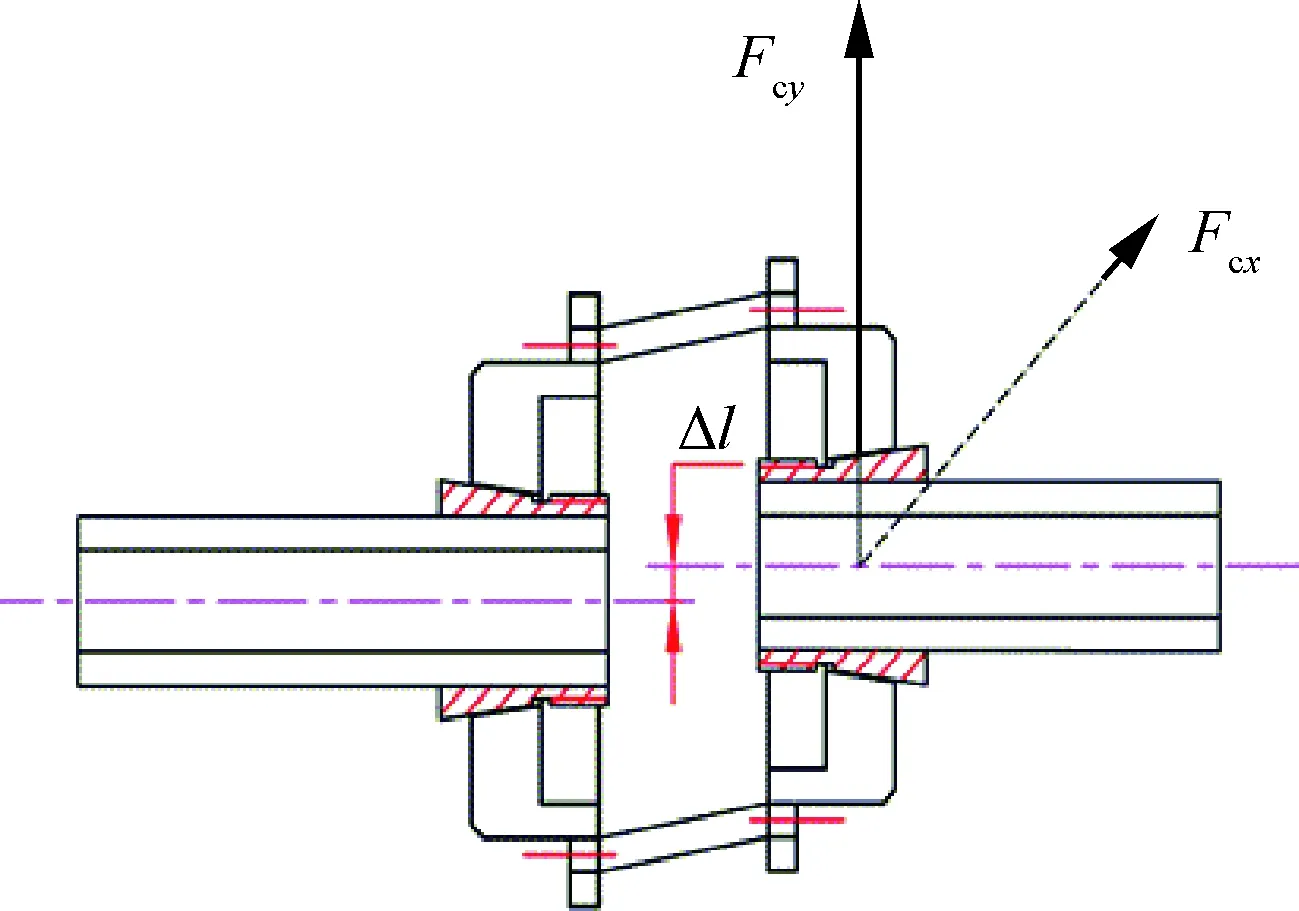
图3 联轴器平行不对中模型

1.4 转子叶片-机匣碰摩模型

旋转机械转-静碰摩的力学模型较多[5-6]，经典的轮盘-约束边界模型未考虑叶片的分布，不能真实反映碰摩振动响应信号特征。真实发动机转子叶尖间隙δd非常小，转子叶片-机匣碰摩容易发生，其物理接触过程可近似简化为图4(a)所示。由于小间隙工况下，叶片-机匣碰摩可能发生叶片断裂，为安全起见，航空发动机实验台的叶尖间隙δd设置较大，碰摩不易发生。通过在机匣一定角位置ϑ处开槽，利用步进电机控制开槽位置处的叶尖间隙δb在小间隙范围内进行局部碰摩，实现碰摩程度的控制，其碰摩物理过程可近似简化为图4(b)所示。

假设低压压气机轮盘的Nr个叶片均匀分布，叶片与轮盘视为刚性盘，叶片-机匣碰摩力等效为集中载荷，不考虑碰撞过程中的复杂物理过程及热效应，图4(a)中的第i个叶片叶尖位置与机匣的径向距离及角位置为

(5)

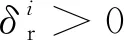
由于实验台初始装配叶尖间隙δd较大，通过在机匣角位置ϑ处开槽，利用步进电机控制开槽位置处的叶尖间隙δb，实现机匣角位置ϑ附近的局部碰摩。因此，图4(b)中的第i个叶片通过碰摩位置处的径向距离表示为

图4 转子叶片-机匣碰摩简化模型

(6)

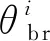
i=1,2,…,Nr

(7)

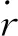
(8)

因此，在x和y方向的碰摩合力可表示为

(9)

1.5 支承轴承力模型

支承轴承力模型如图5所示，滚动体均匀的分布在内外滚道之间，考虑滚动体Hertz接触、时变刚度、间隙，假设轴承内圈与转子过盈配合，外圈与弹性支承连接，滚动体做纯滚动运动，忽略保持架及滚动体惯性运动，不考虑轴承润滑、热效应及轴向运动。支承轴承在水平和竖直方向上的接触力可表示为[20]

(10)

图5 支承轴承力模型

根据牛顿第二定律可获得弹性支承座的动力学方程

(11)

2 双转子系统降阶模型

式(3)是一个较高自由度的非线性时变动力系统，直接数值求解需要大量的计算机时。利用模态综合法对双转子系统进行降阶，缩短系统振动响应的求解时间。

根据支承轴承、碰摩边界、联轴器的位置，将双转子系统的广义坐标q划分为边界坐标qB和内部坐标qi，因此式(3)可表示为

(12)

式中：Mii、Cii、Gii、Kii分别为内部坐标对应的质量、阻尼、陀螺、刚度矩阵；MiB、CiB、GiB、KiB分别为内部坐标与边界坐标关联的质量、阻尼、陀螺、刚度矩阵；MBB、CBB、GBB、KBB为边界坐标对应的质量、阻尼、陀螺、刚度矩阵；式中下标iB和Bi对应的矩阵相同。

根据Craig-Bampton变换关系，系统坐标向量可表示为[14]

(13)

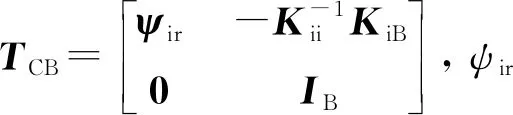
(14)

3 实验台双转子系统振动响应测试

为了研究航空发动机双转子系统的振动响应特性，搭建航空发动机双转子实验系统，如图6所示。该实验系统包括：双转子系统、驱动电机、控制系统、数据采集系统、冷却系统等。双转子系统由轮盘、转轴、叶片、弹性支承、联轴器、内外机匣、支承轴承、齿轮等部件装配而成。该实验台可实现航空发动机双转子系统非线性振动特性研究，以及航空发动机典型机械故障振动特性研究，如不平衡、转/静碰摩、不对中、轴承故障等。主要研究航空发动机双转子系统叶片-机匣碰摩的非线性振动响应特征，相应测试原理如图7所示。

由于实验台高低压转子轮盘都包含了大量倾斜安装的叶片，在运行过程中存在较大的气动阻力，因此实验台的最大转速不超过4 000 r/min。在振动响应测试中，采用5个高精度电涡流传感器测量双转子系统的位移振动，其中4个电涡流传感器分别竖直、水平安装在低压压气机轮盘和低压涡轮盘附近；1个电涡流传感器安装在机匣碰摩位置附近，测量叶片-机匣碰摩过程中的径向振动。数据采集系统的信号采样频率设置为10 kHz，测试过程中通过调节高低压电机转速控制高低压转子的运行速度，并在每个转速下稳定运行40 s左右。

图6 航空发动机双转子实验系统

图7 叶片-机匣碰摩振动响应测试原理

4 数值及实验结果

利用Runge-Kutta方法数值求解降阶模型的振动响应，计算时间步长为0.000 1 s，对比分析不同叶尖间隙、不同转速条件下，叶片-机匣碰摩的振动响应，给出双转子系统叶片-机匣碰摩故障振动响应特征及故障机理，并通过实验进行验证。

图8给出了不同ωL(100、300、400、450 rad/s)，图4中的两个碰摩模型在不同初始叶尖间隙δd(0、5、2 000 μm)下的低压压气机轮盘水平方向的位移响应(xLp)信号。由图8可知，当δd=0 μm时，相同初始条件下，两个碰摩模型在各转速下具有相同的振动波形，因此这种情况下两个模型等价；当δd=5 μm时，两个碰摩模型的振动响应十分接近；当δd=2 000 μm时，两个碰摩模型的振动响应相差较大。因此小叶尖间隙工况下，两个碰摩模型的动力学特性近似等价，大间隙工况下两模型存在较大差别。

由于局部碰摩模型为模型R在碰摩边界上的局部凸起，因此小间隙下，受局部凸起的扰动影响，局部碰摩模型更容易发生失稳。如图8(c)所示，当转速为400 rad/s，局部碰摩模型在δd=5 μm时，3.5 s后系统碰摩响应突然增大，碰摩运动失稳，发生叶片-机匣全周碰摩现象，呈现出干摩擦引起的强烈自激振动；而对于相同叶尖间隙的模型R在该转速下仍是振动量较小的稳定响应；如图8(d)所示，当转速升高到450 rad/s，模型R的振动响应失稳，出现强烈的自激振动。综上，较小叶尖间隙下，碰摩更易发生，图4中的两个碰摩模型近似等价。

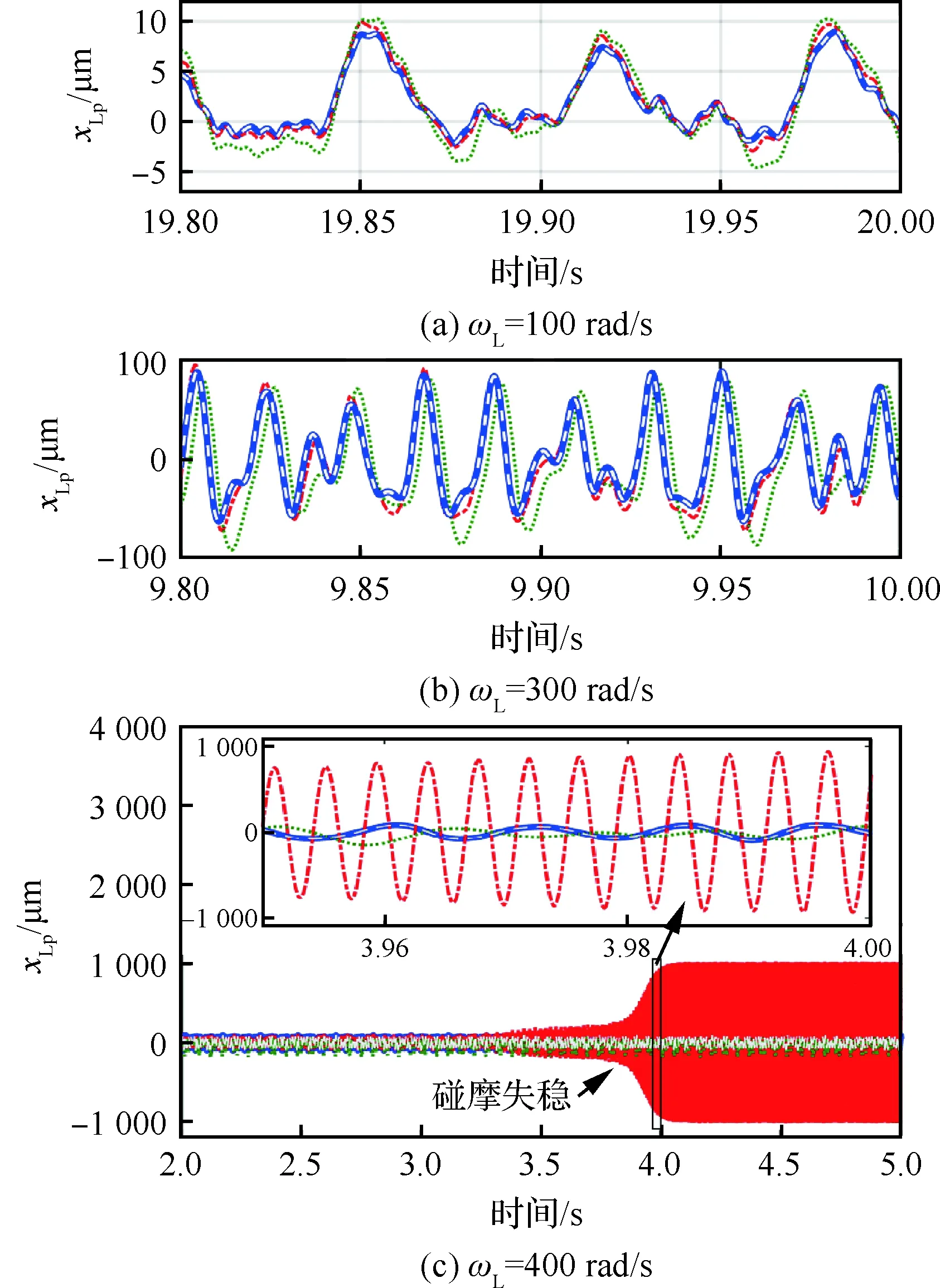
图8 不同ωL低压压气机水平方向的位移响应

图9给出叶片-机匣碰摩失稳时，两种转速比ζ(1.3和1.4)工况下，ωL分别为450、500、550、600、650、700 rad/s的低压压气机轮盘水平方向响应(xLp)的频谱图。由图9可知，随着ωL增加，叶片-机匣碰摩失稳信号的特征频率ωc增加，ωc对应的振幅非常高。

图9 两种转速比工况下叶片-机匣碰摩失稳响应频谱特征

表3和表4给出了不同ωL工况下，ωc与ζ、δd的对应关系。由表3和表4可知叶片-机匣碰摩失稳响应信号的ωc与ζ无关，与δd有关；当δd超过25 μm时，系统不会发生碰摩失稳。但当δd减小至系统发生碰摩失稳时，ωc与ωL成线性比例关系，如图10(a)所示，该比例关系与ζ、δd等参数无关；结合双转子系统坎贝尔图，如图10(b)所示，可知该线性关系的常数项为双转子系统反向进动的一阶临界转速。

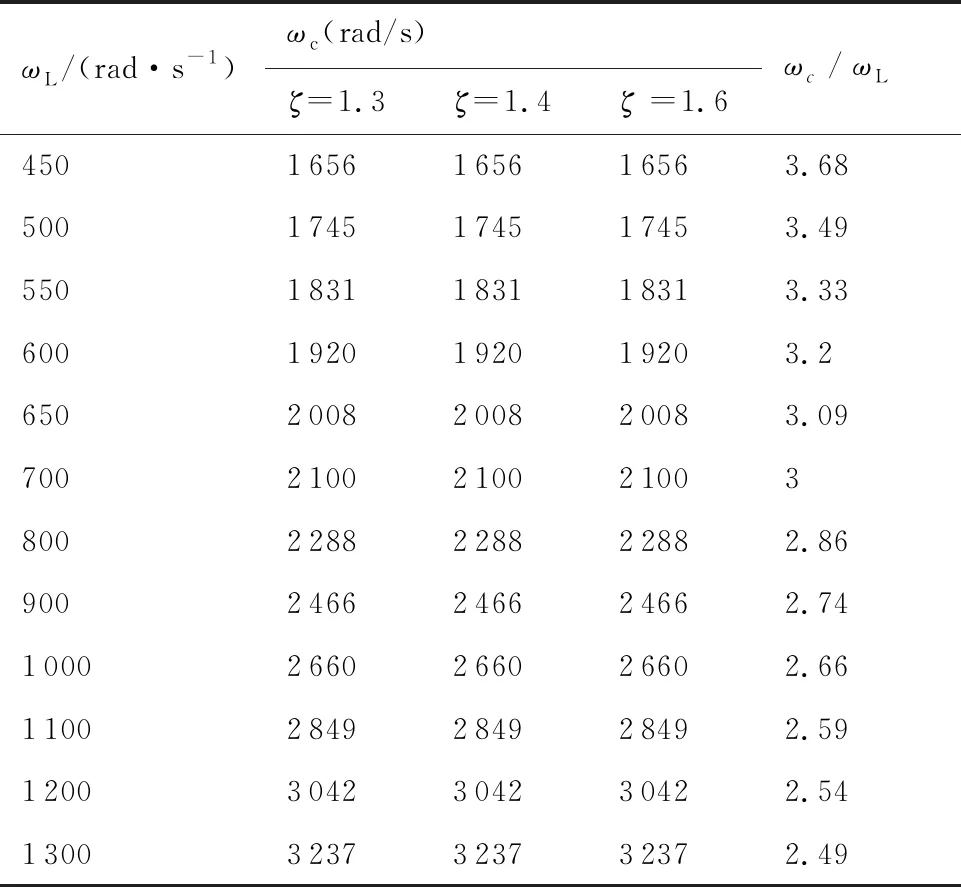
表3 不同ωL下ωc与 ζ 的关系(δd=10 μm)

表4 不同ωL下 ωc与δd的关系(ζ=1.3)

图10 ωc与ωL的关系和双转子系统Campbell图

图11给出了δd=15 μm条件下，低压压气机轮盘竖直方向碰摩位移响应(yLp)的分岔图。由图可知，在[100, 415] rad/s转速范围内系统振动响应为周期性运动，当转速超过415 rad/s后，系统出现失稳运动。结合图12(a)轴心轨迹与图12(c)庞加莱截面可知，在转速400 rad/s时，系统为周期10运动，碰摩响应轨迹超过碰摩边界，表现为全周碰摩；当转速为415 rad/s时，由图12(d)可知，庞加莱截面由10个斑点变为一个封闭的圆环，系统由不稳定的周期10运动发展为稳定的拟周期运动，失稳过程是由干摩擦力激起的反向全周碰摩，该振动为典型的自激振动[22]。然而该振动属于高频振动，失稳特征频率约为低压转子工作转频的2.5～4.5倍，且振动幅值很大，因此具有很大破坏性。如图11所示，系统一旦出现反向全周碰摩，将一直持续下去，失稳转速区域超过900 rad/s，系统在很宽转速区域剧烈振动。因此为避免工作转速范围内发生干摩擦引起的碰摩失稳，叶尖间隙控制对发动机安全运行至关重要。

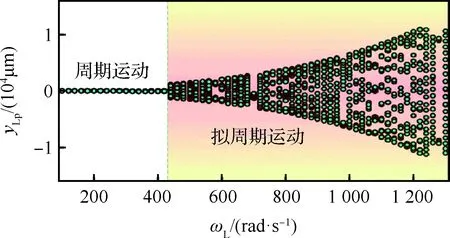
图11 碰摩振动响应分岔图(δd=15 μm)

图12 轴心轨迹与庞加莱截面(δb=15 μm)

图13为数值与实验获得ωL=1 800 r/min、ζ≈1.61、δb=25 μm的局部碰摩位置的径向振动信号(δr)。由图13(a)、图13(b)可知，在相同时间内，数值与实验获得的碰摩位置处的径向位移信号具有相同的波形，当δr超过碰摩位置处的δb时，在碰摩边界处发生接触碰撞。由于系统包含高低压转子的偏心激励、联轴器不对中激励，因此在接触碰撞过程中会出现多个频率组合的冲击响应，数值结果与实验吻合较好。图13(c)和图13(d)给出了碰摩和无碰摩工况下δr的频谱图，由图可知，双转子系统碰摩响应信号频率成分复杂，包含高低压转轴频率fL、fH，2倍频2fL、2fH，3倍频及多倍频，同时还包含高低压转轴频率的整数倍和差组合频率，如：|fL±fH|、|2fL±fH|、|fL±2fH|、|2fL±2fH|等；叶片-机匣局部碰摩特征频率为叶片通过频率fbr及其倍频，并在叶片通过频率两侧存在高低压转轴频率的调制边频带fbr±fL,fbr±fH等；无碰摩与碰摩条件下的频率成分基本一致，但碰摩机匣处的频谱密度比无碰摩情况下高出3个数量级，表明双转子系统与机匣发生强烈的碰摩作用。因此明显的叶片通过率及相应的高低压调制边频带成分可作为局部碰摩的故障特征。

图13 数值与实验叶片-机匣碰摩位置的径向位移响应

图14给出了数值与实验获得ζ=1.3，不同δd的低压压气机竖直方向碰摩响应(yLp)的频率瀑布图。由图可知系统频率成分包含：fL、fH，2倍频2fL、2fH，多倍频及1/3倍(fH-fL)的分数倍频，以及相应的和差组合频率成分，数值与实验的碰摩响应频率成分吻合较好。如图14(a)所示，当δd=20 μm时，系统低压转速超过420 rad/s时，出现碰摩失稳，碰摩特征频率的幅值很大，因此发动机仿真实验台的初始装配叶尖间隙不能小于20 μm；如图14(b)所示，当δd=25 μm时，系统没有出现碰摩失稳，系统振动幅值较小，对碰摩具有一定容忍性；如图14(c)所示，当δd=60 μm时，系统在低压转速超过600 rad/s时，不发生碰摩；结合图14(b)可知，碰摩条件下的振动信号频率成分更丰富，存在1/3倍(fH-fL)的分数倍及其组合频率成分。系统复杂的频率成分主要是由于双转子系统是一个多激励的非线性时变系统，包含多个周期性的外激励，如高低压转子不平衡激励，联轴器不对中激励等；且系统包含多个非线性因素，如轴承非线性、间隙非线性等，从而导致系统振动响应频率成分复杂，其分数倍频率成分是由碰摩非线性引起的故障频率，因此1/3倍(fH-fL)的分数倍及其组合频率成分可作为双转子系统碰摩故障的特征频率。

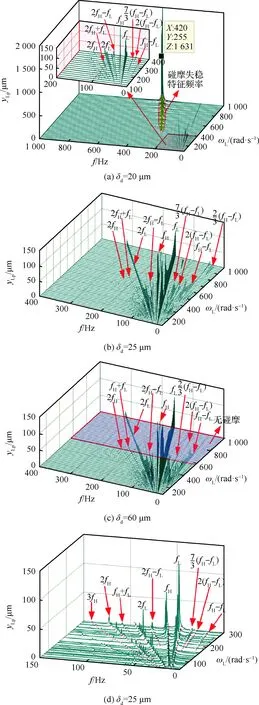
图14 数值与实验低压压气机竖直方向碰摩响应在不同δd下的频率瀑布图

以上是对局部碰摩位置的振动信号特征的分析，下面分析叶片-机匣碰摩的转轴信号特征。图15给出了实验获得ζ=1.2时，碰摩与无碰摩工况下的低压涡轮盘竖直方向位移信号(yLt)的频率瀑布图。由图可知，碰摩与无碰摩的位移响应信号的主要频率成分包括：fL、fH、2fL、2fH，3倍频、多倍频，以及相应的和差组合频率成分，如：|fL±fH|,|2fL±fH|,|fL±2fH|,|2fL±2fH|等，碰摩情况下的转轴横向振动信号频率成分与无碰摩情况下的频率成分几乎完全一致，很难直接区分。

图15 碰摩与无碰摩低压涡轮盘竖直方向位移响应的频率瀑布图(ζ=1.2)

图16给出了实验获得ζ=1.6时，碰摩与无碰摩工况下的低压涡轮盘竖直方向位移信号(yLt)的频率瀑布图。ζ=1.6，碰摩与无碰摩响应的频率特征与ζ=1.2工况下的频率特征一样，主要频率成分为：fL、fH、2fL、2fH，多倍频以及相应的和差组合频率成分，碰摩与无碰摩工况下的频率成分同样几乎完全一致。因此很难通过转轴位置的横向振动信号区分是否发生局部碰摩故障。

图16 碰摩与无碰摩低压涡轮盘竖直方向位移响应的频率瀑布图(ζ=1.6)

5 结 论

1) 结合航空发动机双转子实验系统，考虑叶片-机匣碰摩、支承轴承非线性、转子联轴器不对中及不平衡，利用有限元法建立双转子-轴承-叶片-机匣碰摩系统动力学模型。利用模态综合法缩减系统自由度，数值求解降阶模型的非线性振动响应。数值与实验结果验证了双转子-轴承-叶片-机匣碰摩系统动力学模型的有效性。

2) 航空发动机双转子系统为多激励非线性系统，系统振动响应频率复杂，包括高低压转轴频率、多倍频、组合频率及其他复杂频率，当叶片-机匣发生局部碰摩时，很难通过转轴振动信号的频谱区分是否发生碰摩；但机匣碰摩位置的故障频率为叶片通过频率及其倍频，并在叶片通过频率两侧存在明显的高低压转轴频率的调制边频带，该特征可作为碰摩故障的检测依据。

3) 叶尖间隙对碰摩行为影响很大。当叶尖间隙较大时，不会发生碰摩失稳，但碰摩故障的双转子系统的频率成分更丰富，存在(fH-fL)的分数倍及其组合频率；当叶尖间隙较小时，叶片-机匣碰摩可能发生反向全周碰摩，呈现出由干摩擦引起的自激振动，失稳特征频率幅值很高，其特征频率与低压转轴频率成线性比例关系，该关系在失稳状态下，与叶尖间隙、高低压转速比等参数无关；此外，一旦出现碰摩失稳，系统将一直持续下去，失稳转速范围很宽，危害极大，因此发动机叶尖间隙不能小于引起碰摩失稳的最小间隙。研究结果可为航空发动机双转子系统叶片-机匣碰摩故障诊断及叶尖间隙设计提供一定参考。