海上风机整体耦合疲劳分析影响参数

柏延强，孙泽利，齐晓海，刘 国，王文华，李 昕

(1.中广核研究院有限公司，广东 深圳 518000；2.太原学院，山西 太原 030032；3.大连理工大学，辽宁 大连 116024)

0 引 言

海上风机基础结构的疲劳计算方法可分为时域疲劳分析方法和谱疲劳分析方法：时域疲劳分析是将海上风机的结构时程反应结合雨流计数法、S-N曲线和疲劳累积准则最终得到海上风机疲劳寿命[1]；谱疲劳分析方法基于P-M线性疲劳累积准则，依据疲劳载荷谱和传递函数，得到海上风机基础结构疲劳寿命[2]。由国内外对时域疲劳分析和谱疲劳分析的研究可知，采用时域疲劳分析方法可以得到更精确和合理的结果，因此国内外很多学者对风浪作用下的时域疲劳计算进行广泛研究。

董璐等[3]基于时域耦合计算方法，以浮式风机为研究对象进行疲劳特性分析。曹菡等[4]基于时域耦合计算方法，通过雨流计数法和Miner线性疲劳累积损伤准则得到系泊缆的疲劳损伤。REZAEI等[5]通过S-N曲线、雨流计数法和P-M线性疲劳累积准则得到短期疲劳累计损伤并将结果外推至疲劳全寿命20 a以研究风机运行状态、环境载荷和阻尼变化对疲劳寿命的影响。VELARDE等[6]基于时域耦合疲劳分析方法研究不同水深下波浪载荷对单桩固定式海上风机基础结构疲劳累积的影响。LI等[7]基于海上风机时域耦合数值仿真软件FAST计算结果得到随机风浪作用下Spar式海上风机塔筒和浮式平台的短期疲劳损伤。MOHAMMADI等[8]将损伤表面逼近方法用于计算时域内整体结构疲劳累积，并将其与谱疲劳分析方法进行对比。JU等[9]提出一种基于并行计算技术的海上风机支撑结构耦合疲劳分析计算方法，并对导管架固定式海上风机支撑结构进行疲劳承载力校核。LI等[10]建立一种基于联合概率分布的长期疲劳损伤计算方法，结合C-Vine Copula模型与替代模型实现实际条件下浮式海上风机疲劳损伤计算。

依据海上风机结构时域疲劳分析方法研究现状，本文介绍海上风机时域耦合疲劳计算方法，该方法可以考虑气动、水动力载荷与海上风机结构之间的耦合效应对管节点疲劳载荷及疲劳累积的影响，采用海上风机时域耦合数值仿真工具FAST，通过二次开发名义应力计算模块、管节点应力集中因子(Stress Concentration Factor，SCF)计算模块和管节点疲劳应力计算模块等，结合线性疲劳累积准则提出基于耦合数值仿真模型的疲劳累积计算方法，从而针对海上风机疲劳损伤研究耦合模型计算参数及风浪联合分布的影响。

1 基于耦合模型的疲劳累积计算方法

基于耦合数值仿真工具FAST v8[11]研究海上风机结构耦合分析方法。FAST v8基于叶素-动量理论、莫里森方程、多体动力学和有限元等理论开发气弹分析模块AeroDyn、水动力分析模块HydroDyn、弹性分析模块ElastoDyn、有限元分析模块SubDyn和伺服控制模块ServoDyn等，建立包含转子机舱组件-塔筒-基础结构的整体耦合数值仿真模型。

将由FAST建立的海上风机整体耦合模型与疲劳分析软件Mlife结合，运用Python语言开发基于耦合计算结果的疲劳分析模块，提出海上风机整体耦合模型的疲劳分析方法，技术路如图1所示，具体描述如下：

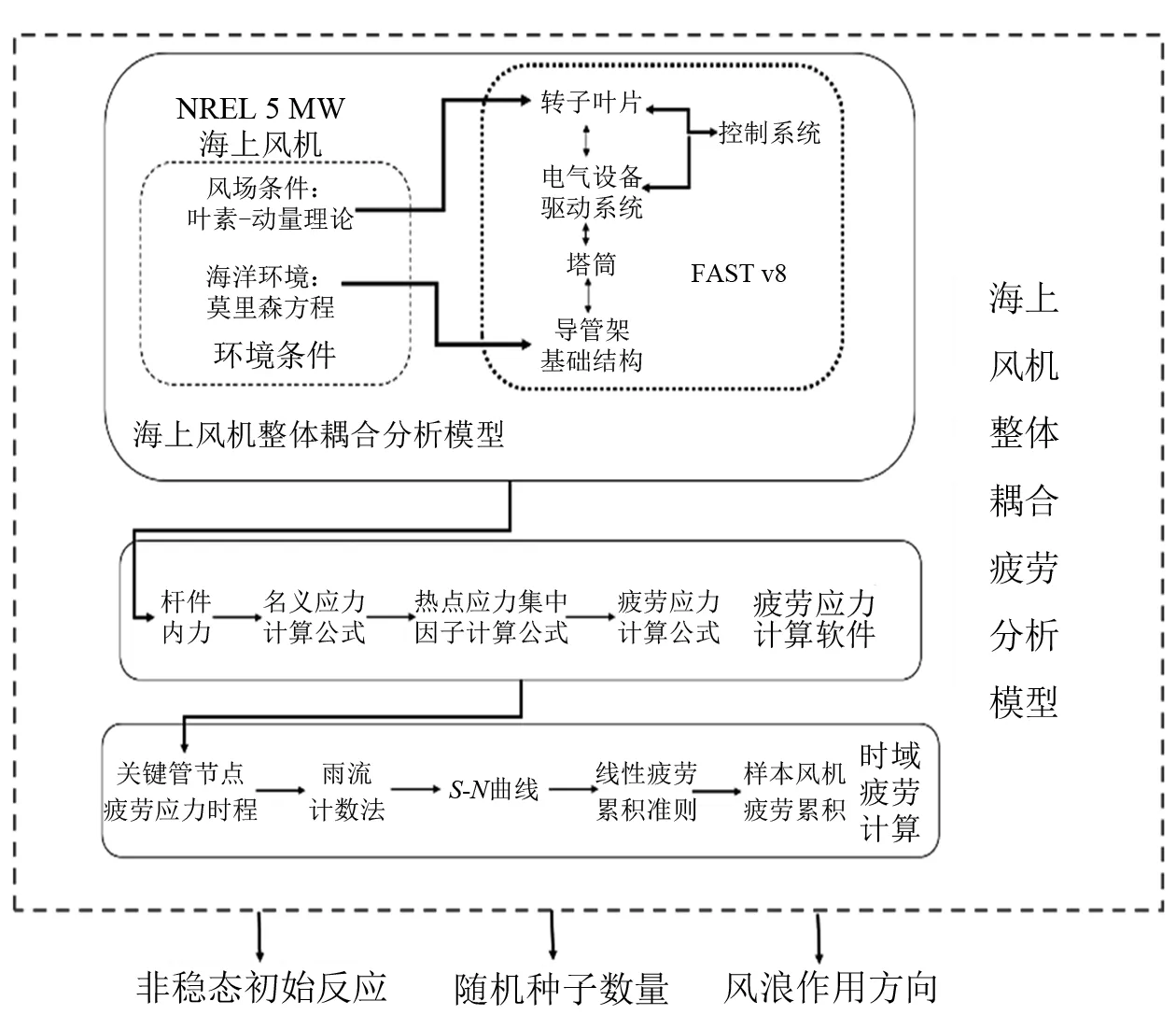
图1 海上风机整体耦合疲劳分析方法技术路线

第1步：选取NREL 5 MW海上风机为研究对象，依据FAST v8[11]建立基于整体耦合方法的包含转子叶片-电气设备驱动系统-塔筒-导管架基础结构的海上风机模型。

第2步：基于典型管节点热点SCF计算公式、名义应力计算公式和热点应力计算公式开发疲劳应力计算模块。

第3步：依据所选风浪联合分布工况，计算风浪联合作用下的关键杆件内力响应。

第4步：基于雨流计数法[12]、S-N曲线[13]和线性疲劳累积准则[13]建立整体耦合疲劳分析模型。

第5步：根据整体耦合疲劳分析方法研究非稳态初始反应、随机种子和风浪夹角对疲劳的影响。

1.1 管节点名义应力计算公式

依据FAST耦合分析所得基础结构杆件内力及杆件截面参数并依据名义应力计算公式计算得到轴向载荷、面内及面外弯矩作用下管节点名义应力。名义应力计算公式为

(1)

(2)

(3)

式(1)～式(3)中：σx、σm,y、σm,z分别为轴向载荷Fz、面内弯矩Mi和面外弯矩Mo所产生的名义应力；d和t分别为管节点直径和壁厚。

1.2 管节点热点SCF

依据海上风机规范DNV GL-RP-C203[13]建议的典型管节点热点SCF计算公式及耦合模型管节点基本参数计算得到模型不同类型管节点SCF。图2为典型T形和K形管节点。

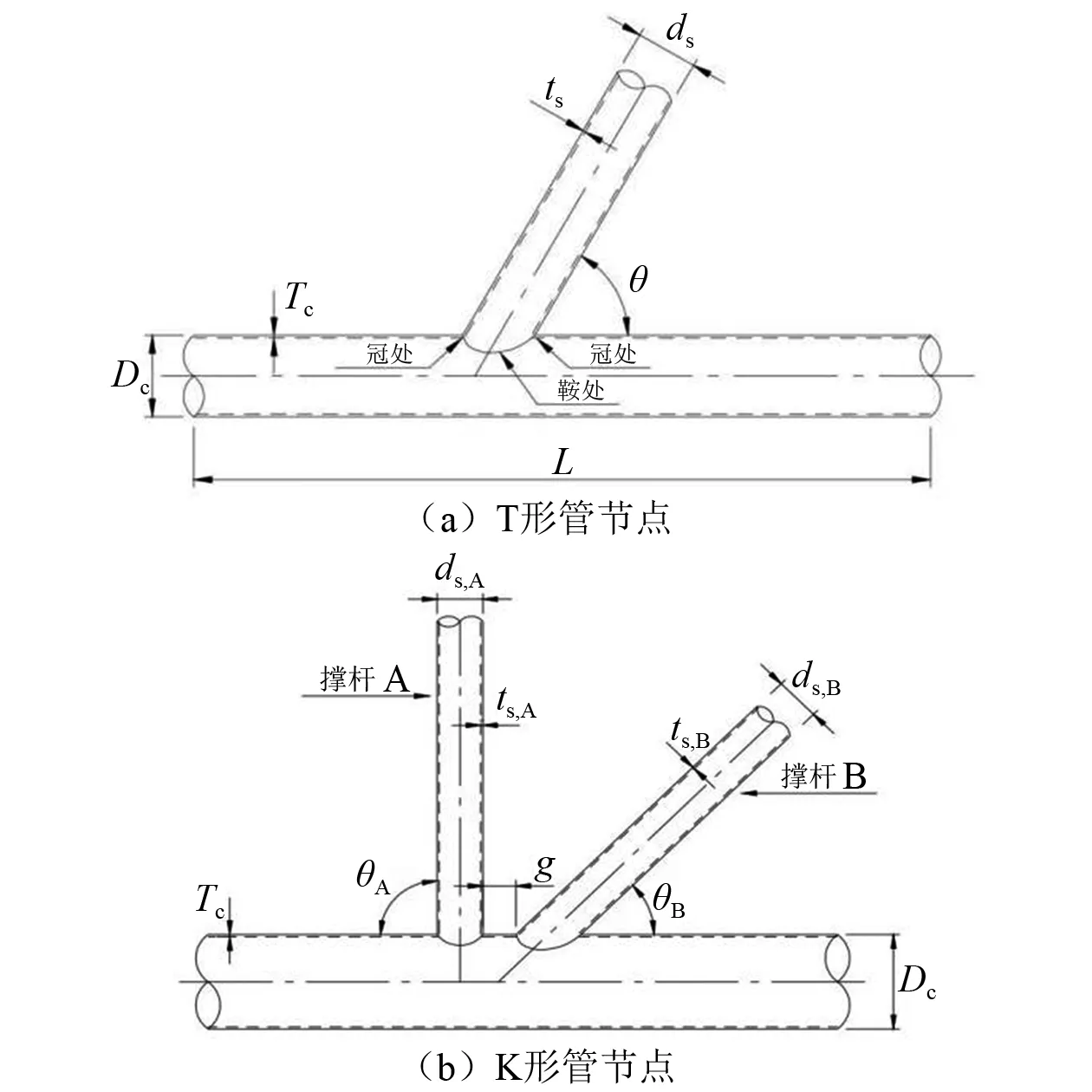
注：L为弦杆长度；Dc为弦杆直径；Tc为弦杆壁厚；ds为撑杆直径；ts为撑杆壁厚；θ为撑杆与弦杆之间的夹角；g为2个撑杆之间的距离图2 管节点几何定义

SCF计算公式为

Fsc,ac=3+γ1.2[0.12e(-4β)+0.011β2-0.045]+
βτ(0.1α-1.2)

(4)

Fsc,as=1.3+γτ0.52α0.1·
[0.187-1.25β1.1(β-0.96)](sinθ)(2.7-0.01α)

(5)

Fsc,mip=1+0.65βτ0.4γ(1.09-0.77β)(sinθ)(0.06γ-1.16)

(6)

Fsc,mop=τ-0.54γ-0.05(0.99-0.47β+0.08β4)·
[1+0.65βτ0.4γ(1.09-0.77β)(sinθ)(0.06γ-1.16)]

(7)

式(4)～式(7)中：Fsc,ac为轴向载荷下冠处SCF；Fsc,as为轴向载荷作用下鞍处SCF；Fsc,mip为平面内弯矩的SCF；Fsc,mop为平面外弯矩的SCF；γ为弦杆直径Dc与2倍弦杆壁厚Tc的比值；β为撑杆直径ds与Dc的比值；τ为撑杆壁厚ts与Tc的比值；α为2倍弦杆长度L与Dc的比值；θ为撑杆与弦杆之间的夹角。

1.3 管节点疲劳应力

依据第1.1和1.2节得到的管节点名义应力时程和管节点热点SCF，采用DNV GL-RP-C203[13]建议的管节点疲劳应力计算公式得到风浪联合作用下管节点疲劳应力时程：

σ1=Fsc,acσx+Fsc,mipσm,y

(8)

(9)

σ3=Fsc,acσx-Fsc,mopσm,z

(10)

(11)

σ5=Fsc,acσx-Fsc,mipσm,y

(12)

(13)

σ7=Fsc,asσx+Fsc,mopσm,z

(14)

(15)

式(8)～式(15)中：σ1～σ8为图3中8个输出位置的疲劳应力。

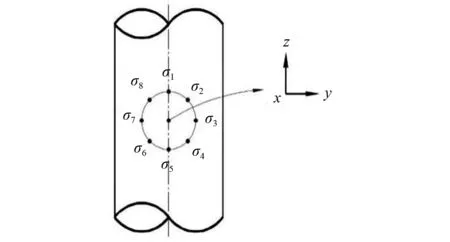
图3 管节点疲劳应力输出位置示例

1.4 疲劳累积计算

S-N曲线[13]表达式为

(16)

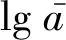
依据雨流计数原则[12]和S-N曲线得到风浪联合作用下样本风机基础结构8个位置处的循环疲劳应力/应力幅和相应的循环作用次数，继而基于Miner线性疲劳累积损伤准则[13]得到海上风机结构短期疲劳累积，计算式为

(17)

式中：Dt为结构的疲劳损伤值；m为结构疲劳破坏时对应的应力级数；Di为第i个应力幅Δσi对应的疲劳损伤；Ni为第i个应力幅Δσi下结构疲劳破坏时相对的循环作用次数；ni为第i个应力幅Δσi下的实际循环作用次数。

2 样本风机及工况选取

2.1 样本风机选取

以我国南海某海域50 m水深海洋环境条件为研究背景，参考NREL 5 MW基准风机[14]和NREL OC4导管架基础[15]提出所研究的样本风机，为满足结构动力特性要求对导管架基础结构进行重新设计，如图4所示，图4也显示本次疲劳分析计算所选取的T形管节点。

图4 海上风机导管架基础

2.2 工况选取

我国南海某海域实测风速和波浪参数联合分布如图5所示。依据图5划分平均风速Uw、有义波高Hs和谱峰周期Tp分布区间，选取累积发生概率为96%[16]的风浪组合工况作为本研究的疲劳计算工况：平均风速区间为4～24 m/s，间隔为2 m/s；有义波高区间为0.25～5.25 m，间隔为0.5 m；谱峰周期区间为2.5～12.5 s，间隔为1 s。

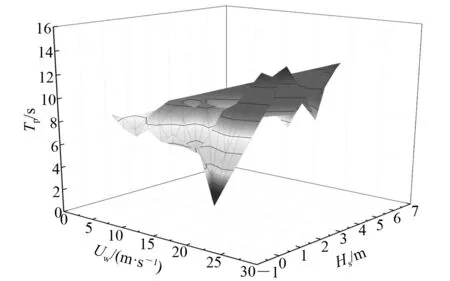
图5 风-浪联合分布

3 样本风机结构动力特性分析及耦合响应机理

3.1 样本风机结构动力特性分析

对导管架基础海上风机耦合计算模型施加白噪声开展动力特性测试，基于塔筒顶部顺风向加速度响应傅里叶谱得到整体结构基频为0.318 Hz，二阶频率为1.705 Hz，具体如图6所示。

3.2 样本风机结构耦合响应机理

采用整体耦合分析方法对整体耦合模型进行耦合分析，选取典型风浪联合作用疲劳设计工况(Uw=11.4 m/s，Hs=1.75 m，Tp=6.5 s)得到基础结构管节点杆件面内弯矩频域响应如图7所示。由图7可知，除整体结构基频和环境载荷频率以外，还可看到3倍转子转速频率3P和整体结构二阶频率的影响，因此环境载荷、转子系统与支撑系统之间的耦合效应对基础结构杆件内力的影响不可忽视，验证了将耦合数值仿真模型应用于海上风机结构疲劳计算的必要性。

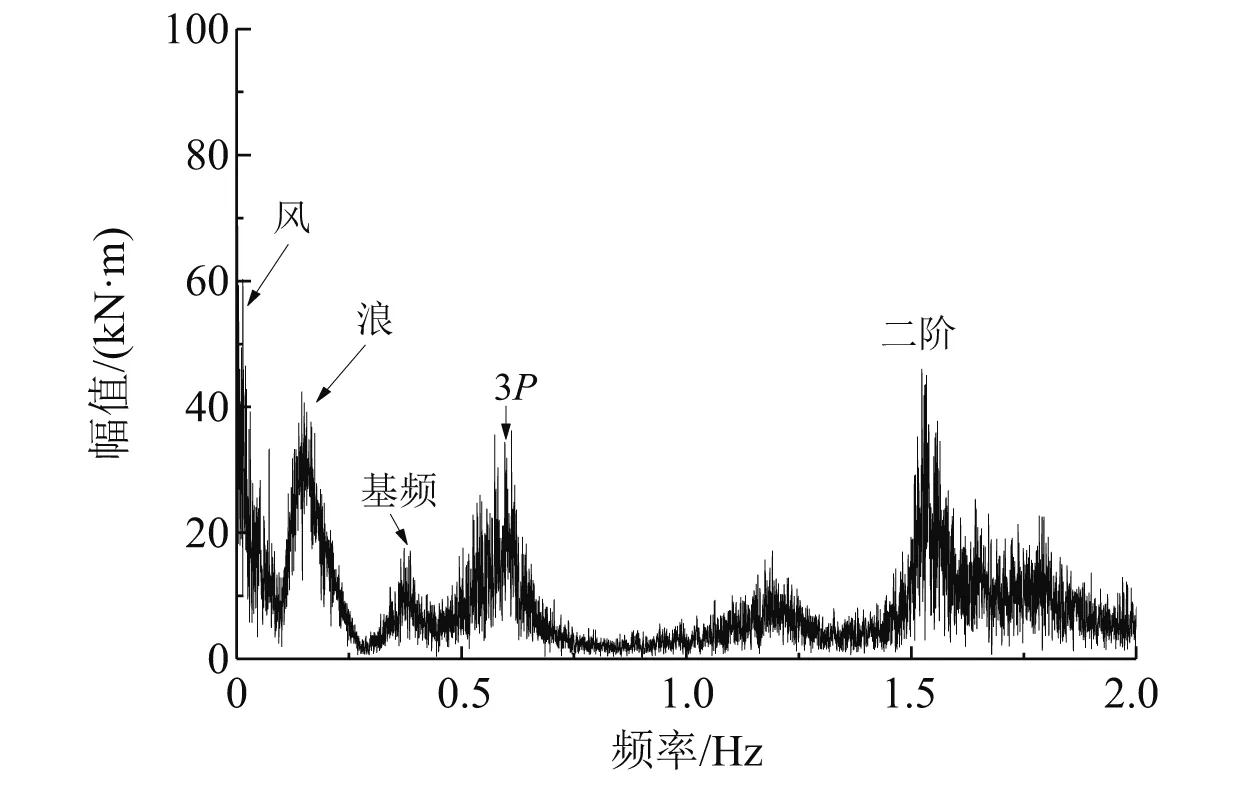
图7 典型疲劳工况下基础结构杆件面内弯矩频域响应

4 海上风机结构耦合疲劳累积影响因素

4.1 非稳态初始反应

选取风浪联合作用工况(Uw=11.4 m/s，Hs=1.75 m，Tp=6.5 s)，研究耦合数值仿真模型非稳态初始反应对疲劳累积的影响，数值仿真时长为3 600 s，拟去除非稳态初始反应时长的选取如表1所示。去除不同初始非稳态反应时长后，得到基础结构管节点等效疲劳应力幅及疲劳累积损伤如图8所示。由图8可知，非稳态初始反应对于管节点等效疲劳应力幅和疲劳累积损伤影响显著，在基于耦合模型开展结构疲劳累积计算时其影响不可忽视。在此基础之上，由图8可知，当去除初始反应时长为30～50 s时，管节点等效疲劳应力幅和疲劳累积损伤趋于稳定。因此，为得到准确的结构疲劳累积，在之后的疲劳累积损伤计算时均选择去除50 s非稳态初始反应。

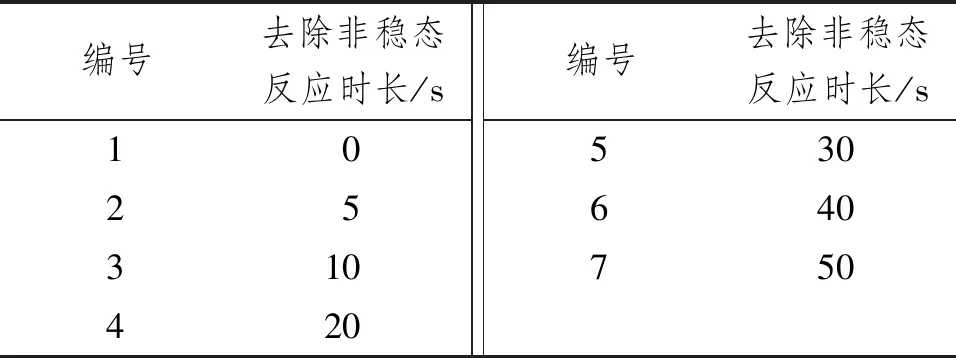
表1 非稳态初始反应时长选取

图8 去除非稳态初始反应时长对等效疲劳应力幅和疲劳累积损伤的影响

4.2 随机种子数量

基于风浪联合作用工况(Uw=11.4 m/s，Hs=1.75 m，Tp=6.5 s)，选取10组不同的随机种子生成具有相同平均风速的随机风速时程以及相同波高、波周期的随机波高时程，研究随机作用下风浪载荷工况对疲劳累积的影响。基于其中5组不同随机种子生成的随机风速时程和波高时程如图9所示。由图9可知，受随机种子影响，各随机风速时程和波高时程变化规律存在差异。因此，研究环境载荷随机性对结构疲劳累积的影响很有必要。

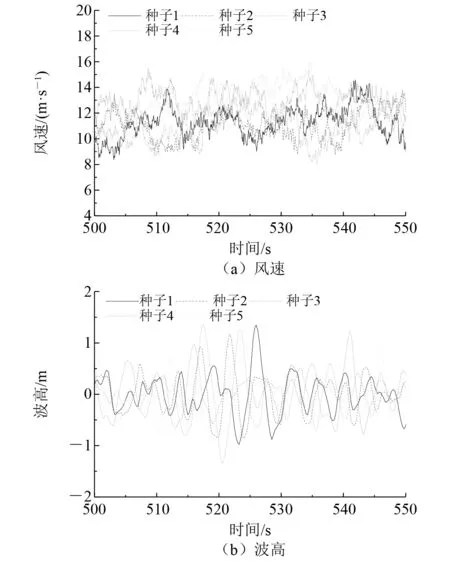
图9 不同随机种子生成的风速时程和波高时程对比

采用整体耦合疲劳分析方法，选取其中5组不同随机种子在位置点1(见图3)处进行疲劳应力对比，如图10所示。

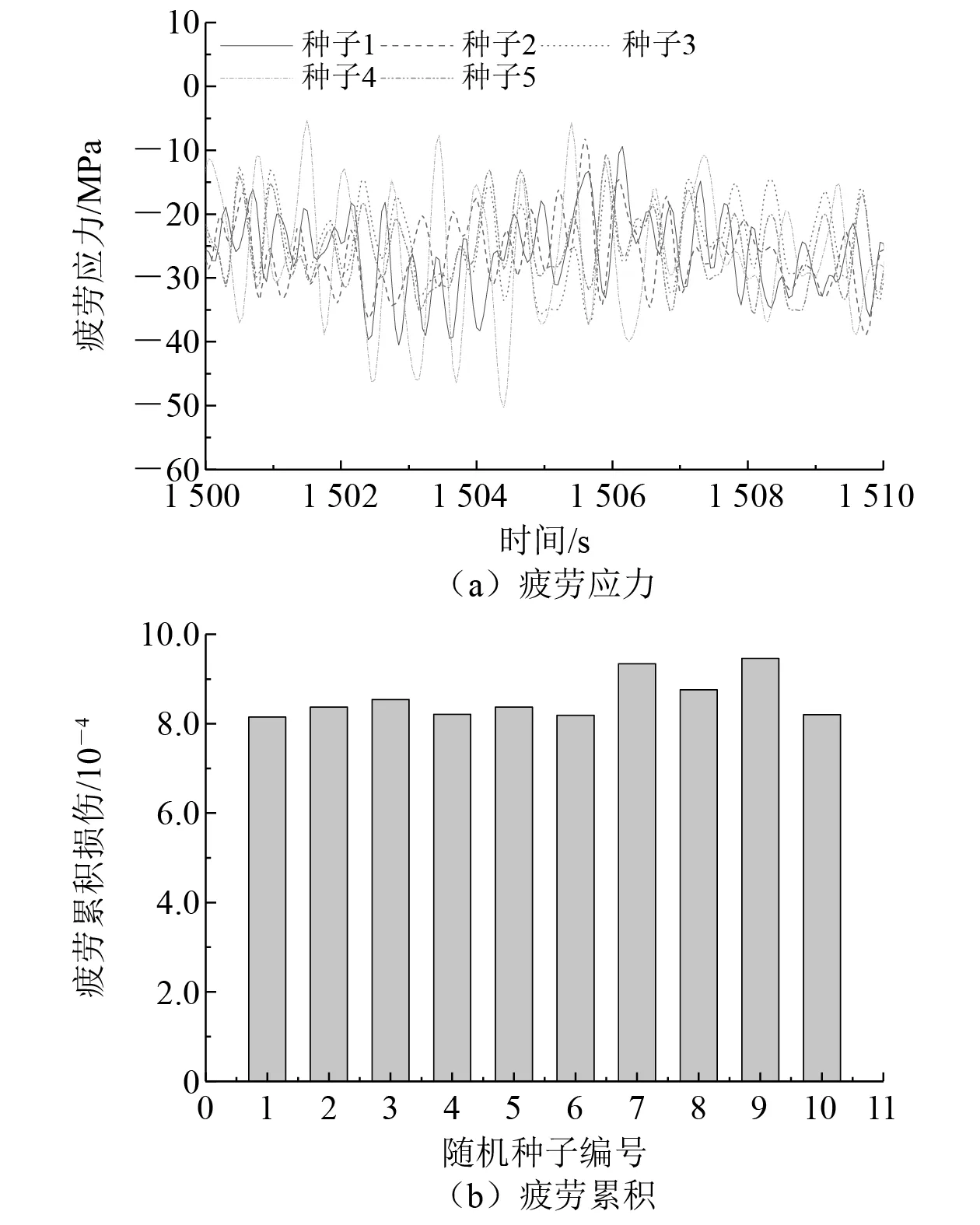
图10 随机种子对于管节点疲劳应力和疲劳累积的影响

由图10(a)可知，在不同随机种子的作用下，具有相同平均风速Uw的随机风载荷以及具有相同波高Hs和波周期Tp的随机波浪载荷联合作用下的海上风机基础结构疲劳应力差异也很明显。由图10(b)可知，受随机种子影响，具有相同平均风速Uw的随机风载荷以及具有相同波高Hs和波周期Tp的随机波浪载荷联合作用下的基础结构疲劳累积同样存在明显差异。

开展随机种子数量敏感性分析，选取不同数量的随机种子的疲劳累积损伤进行比较，如图11所示。由图11可知，在计算基础结构疲劳累积时，须考虑随机种子数量的影响，当随机种子数量大于5组时，所得海上风机结构疲劳累积损伤趋于稳定。为了使结果更合理，在进行海上风机基础结构疲劳累积损伤计算时，至少须选取5组以上的随机种子。

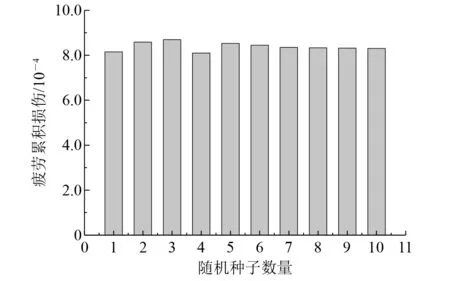
图11 管节点疲劳累积随种子数量变化

4.3 风浪作用方向

选取风浪联合作用工况(Uw=11.4 m/s，Hs=1.75 m，Tp=6.5 s)，开展整体耦合模型疲劳累积计算，其中，风的来流方向为0°，波浪作用方向取0°～90°(间隔为10°)，部分风浪作用方向如图12所示，基于上述工况研究风浪夹角对海上风机结构疲劳累积的影响。

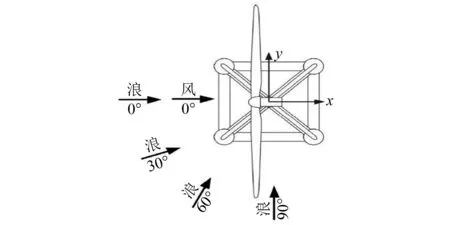
图12 风浪作用方向

当风浪同向及风浪作用方向夹角为30°时，管节点疲劳应力时程对比如图13所示。由图13可知，在不同方向风浪组合作用下管节点疲劳应力时程动力特性发生显著变化，比如当风浪作用方向夹角为30°时，与风浪同向工况相比，波浪频率和结构频率对疲劳应力时程的影响显著降低。

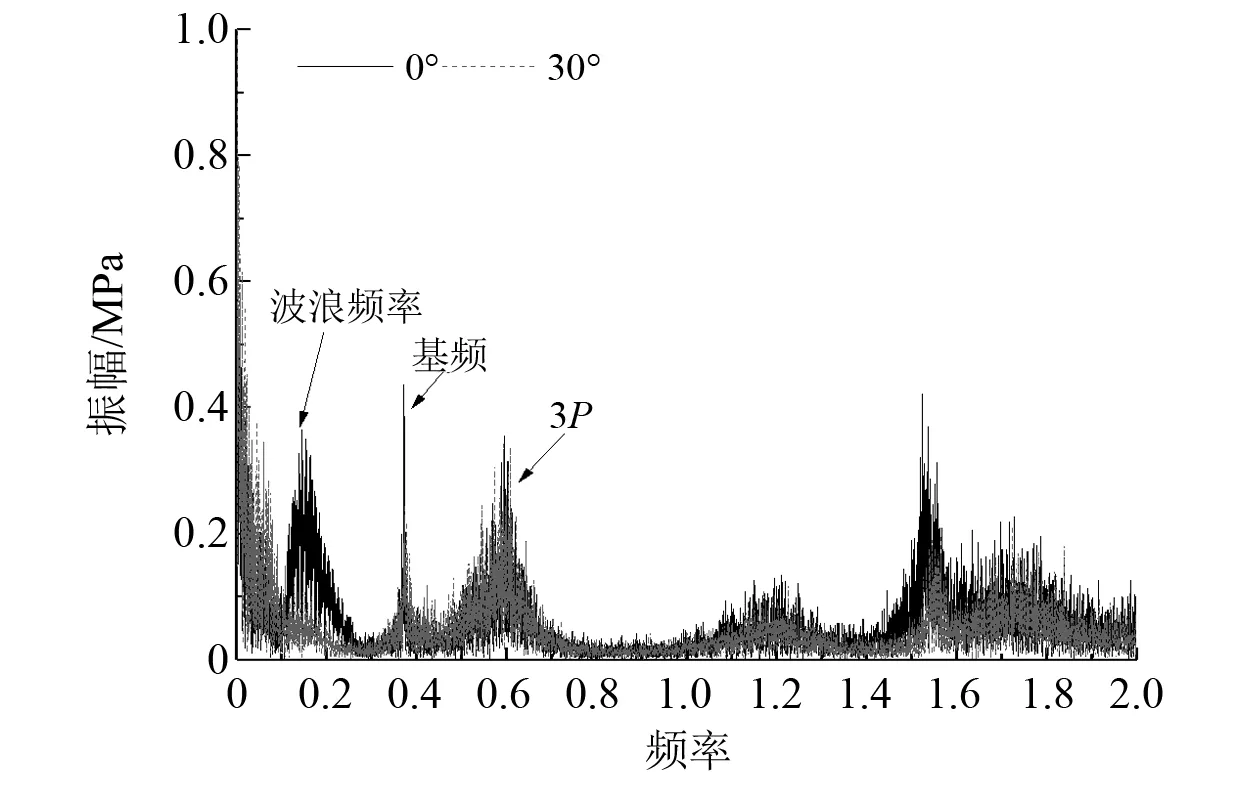
图13 管节点疲劳应力时程傅里叶谱对比

与此同时，不同方向风浪作用下管节点等效疲劳应力幅和疲劳累积如图14所示。由图14可知，与疲劳应力时程响应动力特性相同，管节点疲劳应力幅及相应疲劳累积与风浪作用方向密切相关，不同方向下等效疲劳应力幅及疲劳累积存在显著差异。

图14 风浪作用方向对等效疲劳应力幅和疲劳累积损伤的影响

由上述对比可知，为充分考虑风浪联合分布对结构疲劳累积的影响，有必要基于整体耦合模型开展风浪作用下海上风机结构动力反应分析及结构疲劳累积计算。

5 结 论

在海上风机整体耦合模型的基础上利用时域疲劳分析方法对时域耦合疲劳计算的影响因素进行研究，得到如下结论：

(1) 在计算管节点疲劳累积损伤时须考虑非稳态初始反应的影响，其可造成管节点疲劳累积明显增加。由对比可得，随着去除非稳态初始反应时长的增加，基于耦合模型得到的结构疲劳累积逐步趋于稳定，为保证海上风机结构疲劳累积计算的合理性，基于耦合模型开展固定式海上风机结构疲劳累积计算应考虑至少去除50 s非稳态初始反应时长。

(2) 在计算管节点疲劳损伤时须考虑随机种子和随机种子数量，随着随机种子数量增加，其敏感效果将显著降低，并逐渐平稳。因此，在计算海上风机基础结构疲劳损伤时须至少选取5组随机种子。

(3)风浪作用下海上风机结构耦合响应特性、管节点等效疲劳应力幅存在明显差异，为充分考虑上述差异对结构疲劳累积的影响，有必要开展基于风浪联合分布的海上风机整体结构耦合疲劳计算。